Доповідь "Використання варіативних задач при особистісно-орієнтованому навчанням в професійно-технічних навчальних закладах"

Міністерство освіти і науки України

Державний навчальний заклад

«Запорізький політехнічний центр професійно-технічної освіти»

Предметно-циклова комісія

 предметів природничо-математичних дисциплін

Обмін досвідом:

«Використання варіативних задач при особистісно-орієнтованому навчанням в професійно-технічних навчальних закладах»

Викладач математики

старший викладач     Шоя Вікторія Костянтинівна

Запоріжжя

Введення

Підготовка висококваліфікованих фахівців, конкурентоспроможних на ринку праці, компетентних, відповідальних, вільно володіють своєю професією і орієнтованих в суміжних областях діяльності, здатних до професійного росту та професійної мобільності в умовах інформатизації суспільства та розвитку нових наукомістких технологій, є одним з основних завдань освіти.

Враховуючи, що середня професійна освіта є однією з найважливіших складових сучасного освітнього простору сучасної України, значною мірою впливає на розвиток інноваційної економіки країни, вирішення зазначеної задачі стосовно до підготовки фахівців у закладах середньої професійної освіти набуває особливої значущості.

Це повинен бути безперервний процес самоосвіти, що характеризується прагненням до придбання нових знань, як в виконуваної професійної діяльності, так і в суміжних областях. Необхідною умовою успішності даного процесу є зацікавленість працівника в підвищенні свого професійного рівня, наявність у нього інтересу до виконуваної професійної діяльності, до одержуваної спеціальності, що є необхідною умовою успішності його навчальної діяльності.

На превеликий жаль, на даний момент випускники основної школи не мотивовані на майбутню спеціальність. Вибір установи професійної освіти, в якому вони навчаються або планують навчатися, здійснений або на основі зручного територіального розташування, або за порадою друзів і батьків. Лише деякі учні вибрали спеціальність і освітня установа усвідомлено.

І ось при роботі з таким контингентом на перше місце виходить особистісно-орієнтований напрям у навчанні. Чи можливо це?

Всі ми знаємо, що наш предмет один з найскладніших для учнів та здатності засвоєння знань у всіх учнів різні. Що робити? Як побудувати навчальний процес? Як спонукати учнів до активного і усвідомленому засвоєнню знань? Впевнена, що кожен постійно задає собі ці питання і шукає відповіді на них у власній практиці, в досвіді своїх колег. На допомогу викладачу приходять інноваційні технології навчання. Протягом декількох років працюю над методичною темою «Особистісно-орієнтований підхід у навчанні фізики та математики», хоча кілька років тому тема і називалася по-іншому, але зміст її від цього не змінився. Вибір проблеми обумовлений рядом факторів - актуальність концепції особистісно-орієнтованої освіти не викликає сумнівів.

Теоретичні аспекти використання варіативних задач при особистісно-орієнтованому навчанням в професійно-технічних навчальних закладах

Немає, і не може бути двох учнів, не кажучи про цілу групу, що володіють однаковим набором здібностей, умінь, поведінкових реакцій, мислення і таке інше. Для багатьох з них навіть середній рівень пропонованих вимог виявляється непосильним, зустрічаються, звичайно, поодинокі випадки, коли, учень навпаки, недоотримує знань і розумового навантаження. Але, навіть серед, здавалося б, однаково слабких учнів, одні розуміють викладача відразу, іншим треба повторити, третім необхідно роз'яснити, а деяким повторити, роз'яснити і постійно контролювати і допомагати. Таким чином, успішність засвоєння навчального матеріалу, темп оволодіння ним, міцність осмислення знань, рівень розвитку учнів залежить не тільки від діяльності вчителя, але й від пізнавальних можливостей і здібностей учнів, обумовлених багатьма чинниками, в тому числі особливостями сприйняття, пам'яті, розумової діяльності і фізичним розвитком.

Сучасна освіта - це особистісно-орієнтована освіта, заснована на обліку результатів діагностики індивідуальних особливостей і здібностей кожної дитини, її ставлення до предмета і можливостей його засвоєння, що вимагає від викладача здійснення індивідуального підходу до учнів, передбачення труднощів навчального матеріалу для окремих учнів, підбору раціональних видів робіт для сильних і слабких учнів. Хоча цей поділ проводиться серед тих учнів, які в школі ледве освоювали низький або середній рівні. Але доводиться це робити, по-перше тому, що розумова діяльність все одно у всіх різна, а по-друге за відсутності такого поділу припиняється всяке розвиток особистості. А саме розвиток особистості є основною метою особистісно-орієнтованої освіти. Тому оволодіння теорією і технологією розвиваючого навчання стає необхідною умовою успішної роботи викладача.

Навчання під жорстким або м'яким тиском при твердій дисципліні учнів для всіх однакове за змістом і методикою, беззастережне підпорядкування учня вчителеві були характерні для навчальних закладів протягом багатьох сторіч. Такий стиль відносин "викладач - учень" останнім часом отримав назву авторитарної педагогіки. Але, хоч ця методика і давала свої результати, але в сучасному суспільстві їхнє використання неможливе. Тому потрібно використовувати новітні технології навчання.

Таким чином, серед основних спонукальних причин виникнення та практичного використання особистісно-орієнтованого підходу я виділяю наступні:

1. Необхідність більш глибокого обліку та використання психофізичних особливостей учнів.

2. Усвідомлення нагальної необхідності заміни малоефективного вербального способу передачі знань системно-діяльнісним підходом.

3. Можливість проектування навчального процесу, форм взаємодії викладача та учня, які б забезпечували гарантовані результати навчання.

Переходячи ж до особистісно-орієнтованого навчання, варто зупинитися на кількох його складових.

Урок є особистісно-орієнтованим, якщо на ньому учні є суб'єктами навчання і власного розвитку, і враховуються їх індивідуальні особливості. Особистісно-орієнтоване зміст характеризується особливостями трьох його складових: предметного змісту, технологічного змісту, індивідуального утримання. Предметний зміст має бути умотивований, в ньому встановлені зв'язки, як з минулим досвідом учнів, так і з досліджуваною темою. Технологічний зміст повинен забезпечувати успішність учнів в оволодінні предметним змістом, тому в ньому передбачені загальні підходи до вирішення навчальних проблем, враховуються можливі труднощі учнів та шляхи їх подолання.

При введенні визначення «старі» знання, учнів призводять до «народження» нових об'єктів, аналіз цих об'єктів на предмет наявності істотних властивостей, що дозволяють відрізняти утворилися об'єкти від раніше відомих, призводить до терміну «понятті» і до його визначення.

Аналіз процесів введення різних визначень курсу математики дозволяє виділити три ситуації:

1) в учнів є досвід, на який можна стертися, значить, цей досвід має бути актуалізований;

2) в учнів є досвід, але він суперечить новому, значить, потрібно перебудова наявного досвіду;

3) потрібно формування принципово нового досвіду, тому немає «зачіпок» в наявному досвіді учнів.

Шляхи обліку та збагачення суб'єктного досвіду учнів можна відобразити таким переліком:

1) використання одного і того ж плану роботи з різними поняттями;

2) конструювання знайомих і нових об'єктів за єдиним принципом;

3) використання аналогій між відомими і новими поняттями;

4) залучення інтуїції та здорового глузду;

5) перенесення успішного досвіду учнів у нову ситуацію;

6) аналіз об'єктів на предмет пошуку єдиного властивості;

7) ретельна робота з кожним словом визначення за допомогою спеціальних вправ, що дозволяють сформувати новий досвід учнів;

8) зіставлення декількох можливих ситуацій;

9) звернення до відомих термінів і пошук аналогій в повсякденному житті.

Варіативність при складанні задач для учнів професійно-технічних навчальних закладів дає можливість кожному з них проявити себе навіть при невеликому обсязі знань.

Практика показує високу зацікавленість викладачів училища в психологічному підході до процесу навчання, про що свідчить підвищений інтерес до літератури цього напрямку в будь-яких навчальних закладах загалом, і в нашому училищі зокрема, спроби використання елементів особистісно-орієнтованих і розвиваючих технологій навчання на всіх уроках загальноосвітніх предметів нашого навчального закладу. Отже, перед кожним з нас постійно стоїть завдання створювати такі умови, при яких стало б можливим використання фактичних і потенційних можливостей кожного учня в групі.

Істотною умовою реалізації розвиваючих і особистісно-орієнтованих технологій є організація діалогу, що виводить учня на провідні позиції в навчанні. Для того щоб учень став суб'єктом власного розвитку, необхідно сформувати у нього відкриту пізнавальну позицію.

Метод використання варіативних задач з математики при особистісно-орієнтованому навчанням в професійно-технічних навчальних закладах

Починаючи кожен новий навчальний рік, готуючись до роботи в новій групі, задаю собі питання: Хто такий мій учень? Що він уміє на сьогоднішній день? Які труднощі у навчанні йому зустрічалися в школі? Чи є у нього взагалі бажання вчитися? Бо ні для кого не є секретом, що в професійно-технічні навчальні заклади учні найчастіше йдуть не тому, що дуже прагнуть отримати робітничу професію, а тому, що в школі їх вважали невстигаючими. В наслідок чого майже в кожного з моїх учнів вже вироблений комплекс неповноцінності, панічний страх вийти до дошки, сказати щось не те та стати посміховиськом для інших учнів. Вони тихо ненавидять математику і потай мріють, що їх омине опитування.

При цьому я добре пам'ятаю, що кожен учень, перш за все - людина! Вік моїх учнів – 15 – 17 років. Значить це не просто підліток, а вже майже повністю сформована особистість. І кожному з них потрібно відповісти на питання: Чому вчить мій предмет? І їм мало почути у відповідь: мій предмет потрібен для оволодіння системою математичних знань і вмінь, необхідних для застосування у практичній діяльності, вивчення суміжних дисциплін, продовження освіти; для інтелектуального розвитку, формування якостей особистості, необхідних людині для повноцінного життя в сучасному суспільстві. Він формує ясність і точність думки, критичність мислення, розвиває інтуїцію й логічне мислення, тренує здатність до подолання труднощів. Їм потрібно знати: «Навіщо мені потрібна Ваша математика?». І я намагаюся відповісти на це питання всі три роки навчання, вибираючи завдання з практичним змістом, які чітко доводять, що і робочій людині необхідні знання з математики.

У кожній групі є такі учні, які мають схильність і інтерес до вивчення математики, але тих, хто не мають математичних здібностей набагато більше. Моя робота пов'язана з цілим рядом труднощів. Одна з них обумовлена великою кількістю теоретичних відомостей, які учні повинні були засвоїти в середній школі, але, на жаль, в силу багатьох причин не оволоділи ними навіть на початковому рівні, але і в училищі теоретичного матеріалу дуже багато, а в цьому віці це вже практично не можливо. Тому під час пояснення нового матеріалу я часто не в змозі охопити всіх учнів потребують додаткових роз'яснень, індивідуальної допомоги, коротких екскурсій до шкільної програми.

Собі ж необхідно відповісти на інше питання: Чому я хочу навчити своїх учнів? А хочу я озброїти кожного необхідними для практичної діяльності знаннями, уміннями, навичками; допомогою математики сформувати в учнів логічне мислення, працьовитість, старанність, посидючість, вміння доводити почату справу до кінця. І наводжу на перших уроках вислів Леонардо Ейлера: «Саме математика в першу чергу захищає нас від обману почуттів і вчить, що одна справа - як насправді влаштовані предмети, що сприймаються почуттями, інша справа - якими вони здаються; ця наука дає надійні правила; хто їм слід - той не небезпечний обман почуттів ».

Як же я можу домогтися кращого засвоєння знань моїми учнями? Працюю я давно і в своїй роботі використовую різні технології, але пріоритетною і важливою для мене останнім часом є використання різнорівневих задач при особистісно-орієнтованому навчанні. Хоч це не зовсім правильний вислів для мого метода. Практика підтверджує наявність широкого розкиду індивідуальних відмінностей учнів і як наслідок великого розкиду в рівні засвоєння знань в учнів однієї і тієї ж групи. «Варіативність навчання» - в моєму розумінні це створення найбільш сприятливих умов для розвитку особистості учня, що не встигав в школі, як індивідуальності.

Свою роботу в цьому напрямку я почала з формування бази завдань різного рівня складності. Це досить трудомісткий і безперервний процес, так як межа рівня складності досить умовна і розрізняється від групи до групи. Але сам принцип пропозиції студентам різнорівневих завдань працює безвідмовно. Навіть найслабкіший учень може вибрати собі завдання під силу і відчути задоволення від самостійно виконаною, а не списаної роботи.

Для учнів професійно-технічних училищ звернення до попереднього «досвіду» часто просто неможливо. Тобто на кожному уроці необхідно не вивчати нову тему, спираючись на раніше отримані знання, а організувати роботу так, щоб вивчити цю тему в комплексі старе-нове. Серед моїх учнів переважають ті, кому необхідна постійна консультативна допомога з боку викладача, а як це здійснити, якщо необхідно організувати роботу всієї групи? Дуже допомагають так звані технологічні картки, які розробляються на перших курсах викладачем, а на другому-третьому за допомогою учнів. Основною характеристикою їх є «однаковість» для різних тем. Тобто учні привчаються працювати за певним шаблоном. Так, багато хто може сказати, що таке навчання «вбиває» всяка творчість учнів. Але ж мова йде не про учнів з високим рівнем навчання. Згадаймо, що на навчання в училище приходять діти, не прижилися в школі. Їх рівень знань в кращому випадку середній. А мені необхідно навчити їх основним математичним діям і підготувати до подальшої професійної діяльності. Адже найчастіше, якщо дитина пішов в училище, значить він панічно боїться вчитися, так як в школі завжди був серед невстигаючих, так званих «камчатників». Це забуте слово відмінно характеризує контингент моїх учнів. Тому весь перший семестр моя робота спрямована не стільки на одержання нових знань учнями, скільки на «витягування» назовні пізнавального інтересу, загнаного глибоко всередину середньою школою. З кожним з учнів потрібно з самого початку пройти шлях вироблення основних умінь і навичок математичних міркувань. На етапі вироблення умінь і навичок дуже ефективний «прийом затребуваної допомоги». Він призначений для подолання учнями труднощів на етапах: аналізу умови завдання, пошуку способу його виконання, складання плану рішення, оформлення рішення.

Викладач на першому етапі надає учневі безпосередню допомогу в побудові правильного міркування при рішенні математичної завдання, на другому етапі рекомендації для здійснення відповідного етапу діяльності даються у письмовому вигляді, а потім, на третьому етапі учень отримує картку для самоперевірки виконання даних йому рекомендацій.

Учням повідомляється, що за запропонованим завданням можна запросити допомогу:

1) по теоретичному обґрунтуванню завдання;

2) по проведенню (перевірці) аналізу умови задачі;

3) по проведенню (перевірці) пошуку рішення задачі;

4) з перевірки плану рішення;

5) по перевірці рішення.

Відповідно до запиту буде дана картка, на лівій стороні якої представлені рекомендації, а на правій матеріали для самоперевірки чи інший варіант рішення.

Приклад.

Досліджувати функцію на наявність екстремуму

Крім таких карток я даю різнорівневі задачі, як я їх називаю. Насправді це скоріше задачі з однаковим початком умови та різними закінченнями, кожне з яких передбачає свій розв’язок. Учень на уроці може самостійно обирати свою задачу, яку він в змозі вирішити. Тому він не виглядає «дурнем» серед одногрупників та,найголовніше, перед самим собою. Це найактуальніша задача, що стоїть переді мною у становленні моїх учнів як сильної особистості.

Та повернемося до задач. При закріпленні теми  «Похідна» учні отримують картки, на яких початок задачі однаковий, а продовження та запитання учні обирають самостійно.

Наприклад:

Дано функцію .

• Чи існують похідні функції?
• Якщо існують, то за яким правилом можна знайти похідну даної функції?
• Знайдіть похідну функції.
• Розв’яжіть рівняння .
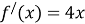• Знайдіть тангенс кута дотичної в точці з абсцисою х₀=2.
• Запишіть рівняння дотичної до функції в точці з абсцисою х₀=-1.
• Чи існують критичні точки функції.
• Знайдіть критичні точки функції.
• Знайдіть проміжки зростання функції.
• Дослідіть функцію на екстремуми.
• Знайдіть найбільше та найменше значення функції на відрізку [2;4]

Необхідно відзначити, що сучасному суспільству потрібні нові педагогічні традиції, переосмислення наявного і наявного досвіду. Я переконана, що педагог сьогодні повинен не стільки навчати, скільки розуміти і відчувати, як дитина навчається, пробуджувати задоволення від процесу навчання. Це і є основне завдання особистісно-орієнтованої педагогіки. Розбудити інтерес до навчання, найголовніша моя задача як педагога.

Я намагаюся використовувати в роботі тільки 3 типи висловлювань, кожне з яких позитивно: 1 - похвалити; 2 - уточнити, направити; 3-пояснити заново незрозумілу частину. Тому, що мої учні і так вважають себе «недалекими», неуками, страшенно закомплексовані і до гикавки бояться вийти до дошки. Тому на перших порах я майже насильно витягаю учня до дошки і всіляко допомагаю йому при відповіді. Тобто роблю все так, щоб після відповіді дитина відчувала свою значимість, задоволення від виконаної роботи.

Але навіть такі методи роботи не для кожного учня підходять. Тому для тих учнів, які не здатні навіть на таку відповідь, передбачено домашнє завдання у вигляді підготовки комп'ютерної презентації по темі, що вивчається або цікавим подіям даного матеріалу.

Учні, які отримали вищий бал, причому це найчастіше не обов'язково вищий бал в системі оцінюванні, можуть працювати з викладачем, самостійно вирішувати стандартні завдання або допомагати товаришам в пошуку і корекції помилок, пояснюючи їх причини. Отже, представляю план-шаблон звичайного уроку-пари по темі:

• Вступне повторення (найчастіше це велика частина часу, ніж на це відводитися в школі);

• Вивчення нового матеріалу (основний обсяг);

• Вивчення нового матеріалу (додатковий об'єм для учнів, які цього потребують);

• Системне закріплення;

• Узагальнююче повторення;

• Контроль;

• Корекція.

На початку уроку або перед початком виду роботи, яку належить оцінити разом з учнями, визначаю, яким чином буде оцінюватися їх навчальна діяльність. При цьому обумовлюються можливі рівні виконання роботи і вимоги, що відповідають кожному рівню, визначаються вимоги до освоєння учнями досліджуваної теми. Вважаю, що на першому курсі, на етапі вивчення нового матеріалу, виконання тренувальних вправ, в процесі пошукової роботи оцінювати учнів некоректно і допустимо тільки у разі значних досягнень. В основному ведеться лише спостереження за ходом роботи, за тим, як ставиться учень до навчання, яка його пізнавальна активність. Якщо учень не впорався із завданням, з'ясовую причини, організую необхідну корекційну роботу з ліквідації прогалин у знаннях і вміннях. Потім пропоную виконати завдання, аналогічне тому, з яким він не впорався, при цьому практично допомагаю йому на кожному етапі вирішення. При складанні перевірочних, самостійних та підсумкових робіт часто обмежуюся завданнями репродуктивного рівня, які повинні входити в роботу для того, щоб учні відчули ступінь матеріалу навчального предмета. Контроль навчальної діяльності направляю на виявлення динаміки набуття знань, розвитку умінь і навичок тільки коли твердо впевнена, що більша частина учнів твердо засвоїла матеріал. Кожен учень повинен утвердитися в думці, що він вміє і знає, як вирішувати завдання. Для мене важливіше простежити динаміку ставлення учня до математики, та й до навчання взагалі. Для відстеження цієї динаміки використовую різні види контролю:

• стартовий;

• прогностичний;

• контроль по результату;

• підсумковий.

Для здійснення контролю навчальної діяльності застосовую різні варіанти складання та оцінювання робіт. Перший варіант – учень сам вибирає рівень і виконує завдання протягом відведеного на виконання роботи часу. Другий варіант – учень вибирає і виконує ті завдання, з якими може впоратися. При цьому він самостійно визначає послідовність їх виконання. Третій варіант – учневі пропонується завдання, яке містить кілька рівнів розумової діяльності. Він самостійно вибирає рівень розумової діяльності, на якому буде виконувати завдання і демонструє необхідні для даної роботи вміння та навички. Динаміка розвитку учнів фіксується при аналізі тестових, тематичних контрольних, самостійних робіт та зрізів, підсумкових контрольних робіт.

Висновки

Особистісно-орієнтований підхід у навчанні учнів професійно-технічних училищ – це найважливіший принцип виховання і навчання, відучення від боязні озвучити свої думки, вийти до дошки, зцілення від клейма невстигаючого, розкриття тих талантів, про яких учень часом навіть не підозрює. А виростання варіативних варіантів подання задач дає змогу розкритися кожному учневі, не залежно від їхнього рівня знань. Він означає дієву увагу до кожного учня, його творчої індивідуальності в умовах урочно-парної системи навчання за обов'язковими навчальними програмами, передбачає поєднання фронтальних, групових і індивідуальних завдань для підвищення якості та розвитку кожного учня. Успішно розвивається пізнавальна активність, інтелектуальна діяльність кожного учня з урахуванням його можливостей і здібностей. Але успіх навчання можливий лише тоді, коли вивчені потреби, інтереси, рівень підготовки, розумові можливості та пізнавальні особливості учня, а також створені оптимальні умови для оволодіння математикою, розвитку здібностей.

І тоді можна з упевненістю сказати:

Математика дозволяє виховувати почуття прекрасного, досконалого, вчить бачити і розуміти оточуючий нас світ, його красу і внутрішню гармонію. Математика робить істотний вплив на естетичні смаки і погляди учнів. Математика виховує сильну особистість, впевнену у собі та власних силах.