Дослідницька робота на тему "Фрактали в природі"

Назва роботи:  «Фрактали в природі»

ЗМІСТ

 

ВСТУП

РОЗДІЛ 1. 

Поняття фракталів…………………………………………………….…6

1.1.  Історія виникнення фракталів ………………………………………..6

1.2.  Що таке фрактал? ……………………………………………………..6

 1.3.  Класифікація фракталів…………………………………………….…8 1.3.1.  Геометричні фрактали……………………………………………..8

1.3.2.  Алгебраїчні фрактали ………………………………………….….12

 1.3.3.  Стохастичні фрактали……………………………………………..12

РОЗДІЛ 2.

Природні фрактали……...……………………………………………….15

РОЗДІЛ 3

Фрактальні криві…………………………………………………………33

 3.1. Як виміряти довжину берегової лінії ?……………………………….....33

 3.2. Берегова лінія озер Острів’янське і Пулемецьке .………………………35

ВИСНОВКИ…………………………………………………………………….36

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ  …………………………………..38

ДОДАТКИ

 

 

 

 

 

 

 

 

 

 

ВСТУП

Природні системи настільки складні і нерегулярні, що використання тільки знайомих об’єктів класичної геометрії для їх моделювання є безнадійним. Як , наприклад, побудувати модель гірського хребта або крони дерева в термінах геометрії. Уявіть, як хитромудро влаштовані легені та нирки , що нагадують за структурою дерева з гіллястою кроною. Нерідко те, що спостерігаємо в природі інтригує нас нескінченним повторенням одного і того ж візерунка, збільшеного чи зменшеного у скільки завгодно разів. Теоретично, елемент розгалуження повторюється нескінченно багато разів, стаючи все менше і менше.Теж саме можна помітити, розглядаючи фотографії гірського рельєфу та берегової лінії . Так проявляється характерна для фракталів властивість самоподібності. У багатьох роботах з фракталівсамоподібність використовується як визначальна властивість. 

Світ, що оточує нас, постійно змінює свій вигляд. Аж ніяк не останній внесок у ці зміни вносить наука, породжуючи нові поняття, нові засоби опису та дослідження звичних або щойно відкритих об'єктів. Понятійний арсенал науки поповнюється часом з надзвичайною швидкістю - так, що вчора ще надійний її інструментарій виявляється застарілим. Інші нові поняття жорстко вибраковуються, і лише минулим сувору перевірку на «виживання» призначено залишити свій слід в науці. Ну а яким-то дано перейти в понятійний базис не тільки «своїй» області знань, але отримати статус міждисциплінарного.

При побудові моделей, що описують навколишній світ, люди звикли використовувати такі відомі геометричні фігури, як лінія, круг, сфера, квадрат, куб і т.д. Але виявилося, що вони не завжди адекватно описують природні об’єкти. Геометрія Евкліда не здатна описати форму хмар, гір, дерев та інше.

Зовсім недавно, у 70-80 роки ХХ століття математики розробили поняття, які здатні описати складні природні об’єкти. Це дозволяє зробити так звана фрактальна геометрія, основним поняттям якої є «фрактал»[6].

Об’єктом дослідження ми взяли берегові лінії озер Острів’янське і Пулемецьке, які входять до складу Шацьких озер.

Предметом дослідження сталифрактальні криві.

Мета дослідження: визначити довжину берегових ліній озер Острів’янське і Пулемецьке.

Особливі геометричні образи та поняття, інколи унікальні,
властиві певному розділу природознавства є основою опису
різноманітних природних явищ. У переважній більшості випадків для
побудови таких об'єктів використовуються традиційні геометрії, зокрема Евклідова,Лобачевського,Рімана.

Проте математики вже наприкінці XIX — на початку XX ст. для побудови неперервних  функцій вивчали та вводили математичні поняття, що виходили за межі традиційної геометрії.

Зокрема, останнім часом широко вивчаються фрактали- геометричні
об'єкти різьбленої форми (лінії, поверхні та просторові тіла), яким властивий особливий характер однорідності та самоподібності. Термін
"фрактал" походить від латинського слова fractus, що значить "дробовий",
"ламаний"[2]. Цей термін увів професор БенуаМандельброт у 1975 p., йому саме належить означення, алгоритм побудови різних типів фракталів, систематизація застосувань фракталів як нерегулярних і самоподібних структур.

Виявилося, що фрактали всюдисущі.Ці об'єкти плідно використовуються в різноманітних розділахприродничо-математичних наук.

 

 

 

 

 

 

 

 

 

РОЗДІЛ 1.  ПОНЯТТЯ ФРАКТАЛІВ

 

1.        Історія виникнення фракталів

Розповів світу про фрактали,  фрактальну геометрію БенуаМандельброт (він і ввів  ці поняття) у 1975 році в книзі «Фрактальні об’єкти: форма, випадковість і розмірність». БенуаМандельброт ( 1924 — 2010) — французько-американський математик єврейського походження. Математик також займався економікою, теорією інформації, космологією та іншими науками. Мандельброт є лауреатом премії Вольфа з фізики у 1993 році, Японської премії за інноваційні ідеї в науці у 2003 році та інших численних нагород.

Мандельброт написав багато наукових робіт з цієї теми, але загальноприйнятим довідником по фракталам є його книга «Фрактальна геометрія природи»(«TheFractalGeometryofNature», 1977) [2].

Об'єкти, які тепер називаються фракталами,  досліджувались задовго до того, як їм було дано таку назву. В  роботах Мандельброта використані наукові результати інших вчених, які працювали в період 1875-1925 роки в цій області (Пуанкаре, Фату, Жюліа, Кантор, Кох, Леві, Хаусдорф та інші).  Проте за браком сучасної комп'ютерної графіки у них забракло засобів відобразити красу багатьох із відкритих ними об'єктів. Кольрові малюнки допоміг виконати  вченому Річард Фос. Завдяки ним і виник такий інтерес до фракталів. З появою цієї книги почався бурний розвиток фрактальної геометрії. Фрактали знайшли майже у всіх природних явищах і процесах.

 

2.        Що таке фрактал?

Строгого і повного означення фрактала не існує. В праці «Фрактальна геометрія природи» Мандельброт дає таке пояснення : «Термін фрактал я сформував від латинського fractus. Відповідне дієслово frangere перекладається як ламати, рушити, тобто створювати об'єкти неправильної форми»[2].  В широкому розумінні фрактал означає геометричну фігуру, яка має властивість самоподібності, тобто складається з частин кожна з яких подібна до всієї фігури в цілому.Якщо кожна частина деякої форми геометрично подібна цілому, то і форма і її каскад називають самоподібними.

У більш широкому сенсі під фракталами розуміють безлічі точок у евклідовому просторі, мають дробову метричну розмірність, або метричну розмірність, відмінну від топологічної. Тобто фрактал - це нескінченно самоподобна геометрична фігура, кожен фрагмент якої повторюється при зменшенні масштабу.

 

 

 

 

 

 

Слід зазначити, що слово "фрактал" не є математичним терміном і не має загальноприйнятого суворого математичного визначення. Воно може вживатися, коли розглянута фігура володіє якими-небудь з перерахованих нижче властивостей:

•           Володіє нетривіальною структурою на всіх масштабах. У цьому відмінність від регулярних фігур (таких, як окружність, еліпс,): якщо ми розглянемо невеликий фрагмент регулярної фігури в дуже великому масштабі, він буде схожий на фрагмент попередньої. Для фрактала збільшення масштабу не веде до спрощення структури, на всіх шкалах ми побачимо однаково складну картину.
•           Є самоподібною або наближено самоподібною.
•           Володіє дробовою метричною розмірністю або метричною розмірністю, яка перевершує топологічну [6].

Багато об'єктів в природі володіють фрактальними властивостями, наприклад: узбережжя, хмари, крони дерев, сніжинки, кровоносна система і система альвеол людини або тварин. Фрактали, особливо на площині, популярні завдяки поєднанню краси з простотою побудови за допомогою комп'ютера.

 

1.3.Класифікація фракталів

1.3.1.Геометричні фрактали

До геометричних фракталів відноситься: сніжинка Коха, множина Кантора, килим Серпінського, трикутник Серпінського, крива Пєано, крива дракона, губка Менгера та інші [6].

Геометричні фрактали – це найбільш наглядні і найпростіші для розуміння. В двовимірному випадку їх отримують за допомогою деякої ламаної кривої (або поверхні для тривимірного випадку). За кожен крок побудови кожен відрізок ламаної замінюється на „криву-генератор” з відповідною зміною масштабу.

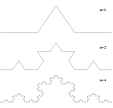Крива Коха  є типовим геометричним фракталом. Процес її побудови виглядає так: беремо одиничний відрізок, поділяємо на три рівні частини і замінюємо середній інтервал рівностороннім трикутником без цього сегмента. У результаті утворюється ламана, що складається з чотирьох ланок довжини 1/3. На наступному кроці повторюємо операцію для кожного з чотирьох отриманих ланок і так далі. Гранична крива і є тріадною кривою Коха.

Тріадна крива Коха також використовується для побудови іншого фракталу – сніжинки Коха. Для цього будується рівносторонній трикутник, і описані вище операції проводяться над кожною з його сторін. При отримується замкнена крива нескінченної довжини, яка охоплює скінченну площу.

 

 

 

 

Сніжинка Коха – на різних етапах побудови

 

Самоподібні множини з незвичайними властивостями в математиці

 Починаючи з кінця XIX століття, в математиці з'являються приклади самоподібних об'єктів.

 Порівняно простий клас прикладів становлять: множина Кантора.

Множина Кантора будується за допомогою видалення середніх третин сегментів прямої. На першому кроці видаляється середня третина із одиничного інтервалу [0, 1], залишаючи [0, 1/3] ∪ [2/3, 1]. На наступному кроці, видаляється середня третина кожного із отриманих інтервалів. Цей процес повторюється до нескінченності. Множина Кантора складається із всіх точок інтервалу [0, 1] які залишаються після всіх повторних видалень. Перші сім кроків зображено вище. 

Трикутник Серпінського — фрактал, один із двовимірних аналогів множини Кантора. Був запропонований польським математиком Вацлавом Серпінським в 1915 році. Цей трикутник один з найбільш ранніх відомих прикладів фракталів. Існує кілька способів побудови цього фракталу. Трикутник Серпінського також називають серветкою або решето Серпінського.

Килимок Серпінського — це плоский фрактал, вперше описаний Вацлавом Серпінським в 1916 році.

Побудова килима Серпінського починається із квадрата. Квадрат розрізається на 9 рівних підквадратів, що утворюють сітку три на три, і центральний підквадрат видаляється. Та ж процедура нескінченно  застосовується до вісьмох квадратів, що залишилися. На ілюстрації нижче показані перші етапи процесу побудови.

Фаза 0     Фаза 1 Фаза 2    Фаза 3 Фаза 4    Фаза 5

 

Крива Пеано — неперервна крива, що проходить через всі точки квадрата.

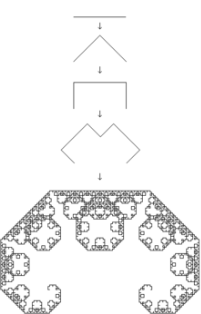Крива Леві — фрактал, який був запропонований французьким математиком Полем Леві, що отримується, якщо декілька разів повторити таки кроки:

 

 

 

 

 

 

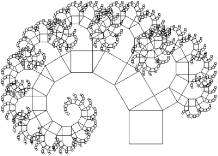
Дерево Піфагора плоский фрактал, заснований на фігурі, що відома як «Піфагорові штани».

 Піфагор, під час доведення теореми, побудував фігуру, де на сторонах прямокутного трикутника розташовані квадрати. В наш час ця фігура виросла в ціле дерево. Вперше дерево Піфагора побудував Босман (1891—1961) під час другої світової війни, з використанням звичайної креслярської лінійки.

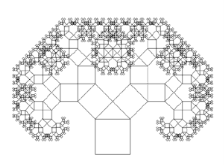Класичне дерево Піфагора

 Однією з властивостей дерева Піфагора є те, що, якщо площа першого квадрата дорівнює одиниці, тоді на кожному рівні сума площ квадратів також буде дорівнювати одиниці.

 Якщо в класичному дереві Піфагора кут дорівнює 45 градусам, то також можна побудувати і узагальнене дерево при використанні інших кутів. Таке дерево називають "обдуваним". Якщо зображати тільки відрізки, що поєднують яким-небудь чином обрані "центри" трикутників, тоді отримаємо "оголене дерево Піфагора".

 

 

 

 

 

Обдуване вітром дерево Піфагора    Оголене дерево Піфагора

 

1.3.2.Алгебраїчні фрактали

Алгебраїчні фрактали це сама найбільша група  фракталів. Один з методів побудови таких фракталів  полягає в наступному. Ви берете формулу, підставляєте в неї число і отримуєте результат. Потім підставляєте в цю ж формулу результат і отримуєте наступне число. Повторюємо цю процедуру багато раз. У математиці це називається ітераційний процес. В результаті виходить набір чисел, які є точками фрак тала [6].

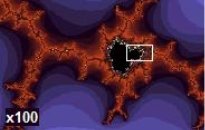
 Найвідоміший алгебраїчний фрактал – це множина Мандельброта

 

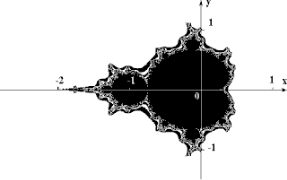
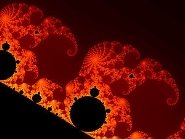
Границя множини Мандельброта є відомим прикладом фрактала

Генерування фракталів

 

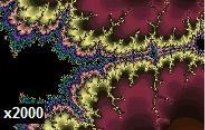
 Навіть збільшення в 2000 разів розкриває деталі множини Мандельброта, які відтворюють всю множину.

Множина Жюліа, фрактал, близький до множини Мандельброта.

 

 

 

1.3.3. Стохастичні (випадкові) фрактали

Стохастичні фрактали отримуються в тому випадку, коли в ітераційному процесі побудови детермінованого фракталу випадково змінювати які-небудь його параметри. Отримані можуть бути використані для генерування берегової лінії, поверхні моря.

  Але для моделювання широкого спектру „природних” фракталів, таких як гори, хмари, поверхні лісових масивів, простої випадкової зміни одного із параметрів побудови статичного фракталу, не завжди достатньо. Для цієї цілі використовують інший клас фрактальних об’єктів, які базуються на фрактальному броунівському русі – випадковому процесі, який дуже широко представлений в природі (броунівський рух маленьких твердих часток в воді).

Графік броунівського руху

 

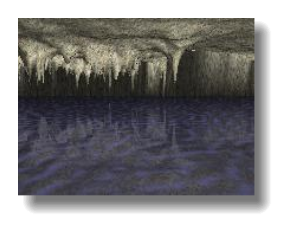
Іще одним відомим класом фракталів є стохастичні фрактали, які утворюються в тому випадку, якщо в ітераційному процесі випадково змінювати які-небудь його параметри. При цьому утворюються об’єкти  дуже схожі на природні – несиметричні дерева, порізані берегові лінії тощо. Двомірні стохастичні фрактали використовуються при моделюванні рельєфа місцевості і поверхні моря.

 

 

 

 

 

 

 

 

 

 

 

 

 

РОЗДІЛ 2. ПРИРОДНІ ФРАКТАЛИ

 

Фрактали у флорі

 Наша планета придатна до життя завдяки зеленим лісам та рослинам. Подивимось на внутрішню структуру листка, в ньому все узгоджено, елементи повторюються і складають єдине ціле. Кожне дерево має стовбур та відгалуження – гілля та листя, без цього його існування неможливе. За таким принципом повторюваності побудована флора нашої планети.

 

Рослинна інженерія. Структура листка.

 Прожилки листя – плоский природний фрактал. Для кожної рослини характерний малюнок унікальний, як унікальний папілярний малюнок на руці людини.

 

Крони дерев.

  Малюнок демонструє фрактальність крон дерев. До речі, проміжки між кронами також мають форму фрактала – це дуже помітно на нижньому негативі.

 

 

 

 

 

 

 

 

 

Дерева-фрактали.

  Можна прослідкувати по 7 розвилок на кожному з чотирьох стовбурів, тобто, це дерево самоподібне в семи різних масштабах розгляду. Розвилка, в якій одна гілка перетворюється в дві – це конфігурація, що повторюється на різних масштабах. З’ясувавши фрактальну суть цього дерева, можна достеменно передбачити, як виглядає дерево в своїй основі.

Екзотичне дерево.

Дерева фрактальні, але тільки в певному діапазоні масштабів. Тут чотири подібні розвилки гілок, а потім фрактальний закон росту гілок, коли доходить до листя, перестає діяти.

 

Баобаб

 Структура баобаба дещо схожа на структуру кровоносної системи легень.

 

Повзучі колючки.    ЯгельЛишайник на камені

.

Самоподібність листка папороті

 Для порівняння, на рисунку показано зображення листка папороті, згенерованого за допомогою фрактальної графіки. Помітно, що і в даному випадку яскраво простежується самоподібність.

 

Пагін папороті.

 

 Навіть більш яскравим прикладом є суцвіття укропу, "парасолька", яка в свою чергу складається з маленьких парасольок.

Важливе спостереження: у вищих рослин, таких, як дерева, більші фрагменти фракталу розташовані в центрі рослини (гілки). В лишайнику навпаки, більші фрагменти розташовані на периферії організму (в дійсності, це колонія організмів).

 

Фрактали в фауні.

 Звернемося до фауни. Вчений-біолог та дослідник Геккель на своїх малюнках зобразив найпростіші мікроорганізми (радіолярії, губки та медузи), що є частиною планктону, порівнявши їх структурну організацію з типологіями відомих фракталів.

 

 Вони дійсно схожі. Так, можна зробити однозначні висновки стосовно самоподібності їх побудови та інваріантності.

 

 

, ,

Фрактальні морські істоти

 Морські мушлі є одними з найяскравіших прикладів фракталів у природі. Вони закручені, елементи повторюють один одного, збільшуються або зменшуються в геометричній прогресії.

 

 

 

 Корали – це продукт діяльності колоній коралових поліпів. Вони на ньому живуть, вони ж його і створюють. Поліпи – невеликі організми, які виловлюють з води планктон. Перетравивши його, вони утворюють мінеральні залишки, так що кораловий скелет колонії постійно зростає.

Корали

 

Фрактали в космосі

 Космос, незвідані галактики, їх системна структура, кулеподібність, планети, що рухаються по колу – все це є фрактальною самоподібністю у всесвітньому масштабі.

 

 

Це червоне «око» Юпітера – загадкове утворення, природа якого до цих пір не з’ясована. Але вже сотню років на ньому спостерігається це око, і єдине розумне пояснення – це величезний вихор розміром більше Землі. Але це ще не все – виявляється, його супроводжують такі ж очі, але меншого розміру, так що Плями на Юпітерітут є ознаки фракталу в атмосфері Юпітера..

 

 

 

 

 

Фрактали  на кухні

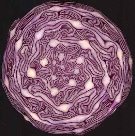
Капуста Романеско.

 Ще один знаменитий  приклад природного фракталу, який наділений математично чіткими формами. Прослідковується як мінімум три рівня самоподібних пірамідок.            

 

 

 

Фрактали в біології

 Найменші клітини живого організму – хромосоми та атоми – є прикладами фракталів. Будова людського тіла заснована на повторенні атомів та молекул, що складаються в органи, тканини та кістки. ДНК – має спіральну самоподібну будову, в якій кожен елемент є важливим. Зміщення навіть одного елементу призводить до втрати всієї структури.

 

 

 

 

 

 

 

Колонії бактерій

 

 

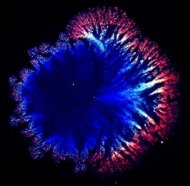
Фрактали в медицині

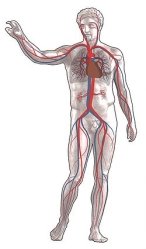
 Система розгалуження нервової та кров`яної систем, бронхи,  будова ДНК, будова мозку – це все приклади фракталів.

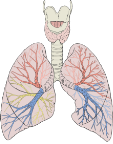
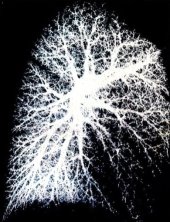
Дихальні шляхи в легенях.

 

 

Кровоносна система легень.

Переплітаються два окремих фрактальних дерева – по одному подається венозна кров, по іншому відводиться артеріальна кров, збагачена киснем. А в сукупності легені – дивуюча за складністю система трьох фракталів – одного дихального та двох кровоносних.

 

Кровоносна система мозку.

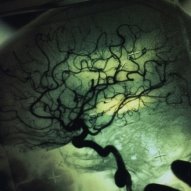
 Це рентгенівський знімок кровоносних судин мозку. Плавні лінії характерні для фракталів, в яких беруть участь потоки рідин.

 

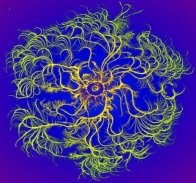
Нейрони в мозку

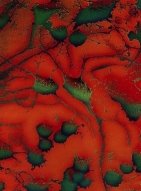 Ви задумувались коли-небудь, що ми буквально мислимо фракталами? Виявляється, мозок зовні має ті ж самі фрактальні ознаки, що і атмосферна хмарність.

Виражену фрактальну структуру мають дендрити – відростки від нейронів. При збільшенні видно, що кожний з них має свої відростки, від яких, в свою чергу, відходять ще більш менші.

 

Тканини мозочку

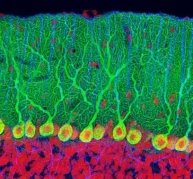Це не абстракційний пейзаж, так виглядають тканини мозочку – одного з розділів головного мозку. Дендрити, що відходять від нейронів, утворюють густі зарослі, дуже схожі на зарослі болотистих листяних лісів. 

 

Сітківка ока

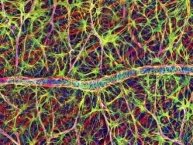Сітківка містить світлочутливі клітини, завдяки яким ми бачимо. На цьому знімку вони жовтувато-зелені. Вони дійсно утворюють сітківку, але ця сітківка хаотична і фрактальна. Рожеві канали – це кровоносні судини, а червоні полоси – тканини, що слугують несучою основою, фундаментом сітківки.

 

Фрактали у неживій природі

 

Гірські каньйони                      Берегові лінії

 Берегові лінії, як правило, мають фрактальну форму, але відрізняються ступенем своєї порізаності. На даному прикладі видно дві характерних властивості природних фракталів: окремі протоки не є копією один одного, наче вони намальовані одним лекалом. Великі протоки аналогічні за окресленням маленьким протокам. Якщо ми збільшимо, наприклад, нижній лівий кут малюнка, ми отримаємо дещо схоже на весь малюнок цілком.

 

 

Дивлячись на форму берегової лінії зблизька, можна з певною достовірністю передбачити характерні обриси лінії берега

 

 

 

Іспанські болота.

Земля і вода.Взаємодія землі і води породжує фрактальні структури ландшафтів.

 

Пісок і вода.

 Коли піщана дюна розмивається водою, в дрібних масштабах повторюється те, що придає фрактальну форму більшим земним ландшафтам

 

 

  Піщана буря.                   Гірські хребти. Вид з космосу.

 

Сніжинки

 

 

Утворені на склі морозні візерунки.

 Іноді утворюються дивні картини, які більш типові для рослинного світу.

 

 

Деревовидний фрактал

 

Водні каскади

Хмари

 

 

 

Атмосфера

Що відбувається в атмосфері, можна побачити тільки тоді, коли супроводжується хмарністю. Структури хмар фрактальні, але це тільки те, що ми бачимо.

 

Турбулентність

Турбулентність – це порушення рівномірного потоку газів або рідин, коли вони починають завихрятися, бурлити. Як правило, це відбувається, коли потік налітає на перешкоду.

 

 

Блискавки

 

Слід від удару блискавки. Блискавка залишає дуже характерні сліди. Коли люди виживають після удару блискавки, у них на шкірі залишаються точно такі ж самі відмітини, тільки менші за розміром.

 

Розряди в магнітному полі

 

Розряди в газорозрядній трубці (на відміну від блискавок та штучних електричних розрядів на вільному повітрі, він дуже щільний).

 

 

 

 

Слід розрядів на дереві.          

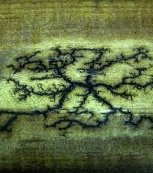Береться джерело імпульсів високої напруги та дерев’яна дошка. Дошка змочується сольовим розчином, потім до неї прикріпляється один з електродів джерела. Другий закріпляється над дошкою на відстані декількох сантиметрів. Розряд починає вимальовувати на поверхні дошки затійливий фрактал, дуже схожий на дендрити в мінералах.

 

Сталактити, сталагміти

 

Тріщини

Тріщини в сухій глині. Дуже красивий фрактал, схожий на текстуру шкіри. В ньому всього два рівні самоподібності – а вся справа в тому, що товщина шару глини, яка спочатку намокає і набухає, а потім висихає і тріскається – невелика.

 

Тріщини на льоду              Тріщини на пательні, коли                                            

потріскався шар нагару

Фрактальні тріщини з'являються на DVD диску після обробки мікрохвильовим випроміненням.

 

 

 

  Пузирі

 

 

 

 

Візерунки на склі.

Цей фрактальний візерунок отриманий досить просто: на одне скло налили в’язку та непрозору рідину, потім приплюснули другим склом, так щоб два скла злиплись. А потім скло розділили. В момент розз’єднання повітря потрапило в щілину і утворило у в’язкій рідині такі фрактальні візерунки.

Дендрити – деревовидні утворення в мінералах. Виникають при швидкій кристалізації рідкої та газоподібної речовини.

 

 

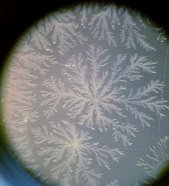
Нанодендрити срібла. Ці срібні сніжинки вирощені штучно в рамках нанотехнологічних досліджень. Скляна поверхня з такими сніжинками має властивості оптичного фільтру, який може фільтрувати електромагнітні випромінювання певної довжини. З наукової точки зору, це дендрити срібла, які отримані шляхом осіданням парів срібла на скляну поверхню.

 

Дендрит магнію. Це штучний дендрит магнію, який був отриманий шляхом осідання парів магнію на холодній поверхні. Дуже нагадує шишки або кокоси.

Дендрит золота. Золотий самородок – створений самою природою.

 

 

 

Карбонат-апатит. Приклад фрактальної структури в мінеральному світі, яка не схожа на звичайні кристалічні або дендритні структури. Більше схоже на піну або органічні  форми.

 

Дендрит міді. Шматок самородної міді з окисленою поверхнею

 

 

Високовольтний розряд в блоці акрилу створює фрактальнийрисунок Ліхтенберга [6].

 

РОЗДІЛ 3 ФРАКТАЛЬНІ КРИВІ

 

3.1. Як виміряти довжину берегової лінії

Ступінь «порізаності», «зламаності», «хвилястості» фрактала може бути виміряне числом, яке називається фрактальна розмірність. З допомогою фрактальної розмірності можна порівнювати фрактали між собою. Вона збільшується із зростанням «порізаності», «зламаності», «хвилястості» об’єкта, тоді як топологічна розмірність не враховує всі зміни, які відбуваються з лінією чи поверхнею.  Головна особливість фракталів, що їх розмірність є дробовим числом. Поняття фрактальної розмірності було введено Феліксом Хаусдорфом і Абрамом Безіковичем. Відтепер вона заслужено носить імена своїх відкривачів — «розмірність Хаусдорфа-Безіковича».

Прикладом  фрактального об’єкту, що часто зустрічається в природі, є берегова лінія.  В географічних масштабах берегові лінії можна моделювати з допомогою фрактальним кривих [3].

Як вже було зазначено раніше, незмінність відносно масштабу характерна особливість фракталів.  Але далеко не всі фрактали мають властивість самоподібності.  Багато фракталів,  що зустрічаються в природі не мають такої властивості. Вони відтворюють у кожному фрагменті статистичні властивості цілого.  До таких фракталів відносяться берегові лінії країн.

Виконані в різних масштабах карти відрізняються в конкретних деталях, але загальні їх властивості залишаються незмінними.

У 1977 р. Бенуа Мандельброт поставив перед собою наступне завдання: чому дорівнює  довжина берегової лінії Великобританії? У 1988 р. норвезький учений Енс Федер вирішив з'ясувати, чому дорівнює довжина берегової лінії Норвегії, при тому що побережжя Норвегії сильно порізане фіордами.  Інші учені ставили собі аналогічні питання про довжини берегових ліній побережжя Австралії, Південної Африки, Німеччини, Португалії та інших країн.

  Ми можемо зміряти довжину берегової лінії тільки приблизно. Якщо подивимося на космічні знімки морського узбережжя, то побачимо затоки і півострови.  Якщо  поглянемо на нього з висоти пташиного польоту, то нам буде видно вже  бухти та миси. А якщо пройдемося по узбережжю, то побачимо камінчики, які далі видаються в воду, ніж інші.

Тому,  якщо ми обчислюємо довжину берегової лінії, то потрібно обов’язково вказувати по карті якого масштабу вона вимірювалась.

Одне з найбільш ранніх відкриттів вченого - нескінченна довжина берегової лінії будь-якого острова. Саме так. Але як же так, запитаємо ми?І подивимося на наші вимірювальні прилади.

Виявляється, якщо наша лінійка довжиною в 100 м - навколо острова поміститься 19 раз, то довжина його берегової лінії буде 1900 м. Якщо наша лінійка довжиною в 10 м, вона зможе поміряти більш дрібні западини і бухти - на береговій лінії,  поміститься 242 рази, а довжина берегової лінії складе 2420м. Якщо ми візьмемо лінійку в 1мм, то зможемо проміряти кожен камінчик - довжина берегової лінії при такому вимірі буде

5423 м - втричі більше першої величини.

 

Яка ж довжина правильна, запитаємо ми? «Ніяка, довжина берегової лінії нескінченна», - усміхнеться Бенуа. Чим менше буде наша лінійка, тим більше буде довжина. При лінійці, що прагне до нуля, довжина лінії буде нескінченною для будь-якого острова, хоч для Цейлону, хоч для крихітного острова Сіпадан.Мандельброт задався питанням, як порівняти два острови, якщо очевидно, що вони різні. І ввів нову величину - фрактальну розмірність (насправді це переосмислена їм розмірність Хаусдорфа) .Фрактальная розмірність - міра деталізації, міра нерівності фрактального об'єкта. Розмірність у фрактального об'єкта завжди більше топологічної (звичайної) розмірності і може бути (найчастіше і є) дробовою.

3.2. Берегова лінія озер Острів’янське і Пулемецьке

       Берегова лінія озера Острів’янське, яке входить до складу Шацьких озер, має багато заглибин і виступів. Берегова лінія озера Пулемецького, яке також входить до складу Шацьких озер, плавна, заокруглена.

За допомогою географічних карт перекреслимо берегові лінії даних озер в масштабі 1:20000 для озера Острів’янського і в масштабі 1:40000 для озера Пулемецького. Нанесемо дотичні до берегових ліній з різною довжиною кроків та обчислимо довжини берегових ліній озер( таблиця 1, додаток А, Б,В,Г).Побудуємо графіки залежності довжини берегових ліній від довжини кроку (додаток Д, Е).

Проаналізувавши дані таблиці 1 та графіки приходимо до висновку, що із зменшенням кроку довжина берегової лінії для озера Острів’янське зростає, а довжина берегової лінії для озера Пулемецьке спадає.Таким чином, графік залежності довжини берегової лінії від довжини кроку для тих берегів, які мають виступи,заглибини буде спадним, а графік залежності довжини берегової лінії для берегів з плавним переходом буде зростаючим.

Отже, фрактальна розмірність берегової лінії буде залежати від її форми.

 

 

 

 

 

 

ВИСНОВКИ

 

Фрактали- це наукова  краса або красива наука , якою насолоджуються у всьому світі у різних сферах життя.  

Фрактальна геометрія дуже важлива для опису природи. У своїй книзі  Мандельброт з цього приводу писав: «Багато форм Природи настільки неправильні і фрагментовані, що в порівнянні з евклідовими фігурами Природа демонструє не просто більш високу степінь, але повністю інший рівень складності» [2].

 В хаосі, який нас оточує, насправді існують ідеальні форми. Природа є найкращим архітектором, ідеальним будівельником та інженером. Вона влаштована досить логічно, і якщо ми не можем знайти закономірності, це не значить, що їх не має. З упевненістю можна сказати, що фрактали зберігають ще немало таємниць, які нам належить відкрити.

Присутність фрактала з першого погляду можна і не помітити, якщо не заглиблюватись у досконале вивчення математики. Ця наука, дійсно, не має меж і постійно спонукає до різноманітних досліджень.

Фрактал — це математична величина, що зустрічається досить часто. Абсолютно точна, алгебраїчна величина, яка творить собою неймовірні фігури, візерунки та складає цікаві орнаменти, що ми зустрічаємо кожного дня. Це і листя папороті, і маленькі сніжинки та ще багато іншого.

Галілео Галілей у 1623 році писав: “Вся наука записана у цій великій книзі, — я маю на увазі Всесвіт, — що завжди відкрита для нас, але яку неможливо зрозуміти, не навчившись розуміти мову, якою вона написана, а написана вона мовою математики, і її літерами є трикутники, кола і інші геометричні фігури, без яких людині не можливо розібрати жодного її слова; без них вона подібна блукаючому в пітьмі…”

Введення поняття фрактала змінило багато традиційних уявлень про геометрію, а в історії розвитку математики стало переломним моментом. З кожним роком поняття фрактала стає відоме все більш широкому колу людей. І зараз цей термін важко залишити без належної уваги. У природі є багато чого, що має прямий зв’язок до цього терміну.

Присутність фрактала з першого погляду можна і не помітити, якщо не заглиблюватись у досконале вивчення математики. Ця наука, дійсно, не має меж і постійно спонукає до різноманітних досліджень.

«Все так складно, все так просто» влаштовано вприроді, помічають люди, з повагою прислухаючись до неї. «Природа наділила людину прагненням до виявлення істини»,- писав Цицерон. Спостереження за навколишнім світом наштовхує нас на думку про те, що всі складові елементи об’єктів з навколишнього світу повторюють самих себе, але в певному масштабі.

Робота над науково-дослідницькою роботою дала можливість розширити  та поглибити знання про об’єкт дослідження - фрактальні криві, їх властивості, способи створення та використання. Поставлена мета досягнута. При обчисленні довжини  берегових ліній озер Острів’янське і Пулемецьке, яківідповідно приблизно дорівнюють9 км і 14,4 км, було досліджено залежність зміни довжини берегової лінії від складності її форми.У статтях про водні ресурси вказується довжина берегової лінії озера Острів’янське -9.3 км і озера Пулемецьке- 16км , що входять до водних ресурсів Волинської області.

Надалі планується продовжити досліджувати загальні формули побудови фракталів і за допомогою цих формул визначати фрактальні розмірності берегових ліній.

Теорія фракталів -  дуже молода наука, яка бурхливо розвивається  і  перед якою стоїть велика кількість цікавих і поки що нерозв’язаних проблем, які чекають на молодих і талановитих дослідників.

 

 

 

 

 

 

 

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

 

1.                   Божогин С.В., Паршин Д.А. Фракталы и мультифракталы. М.: РХД, 2001. 128 с.
2.                   Mandelbrot B. The Fractal Geometry of Nature. W.H. Freeman, San Francisco, 1982. 468 с. (Русский перевод: Бенуа Мандельброт. Фрактальная геометрия природы. М.: Инст. компьют. исслед. 2002, 654 с.
3.                   [Електронний ресурс]: / Режим доступу: http://webecoist.com/2008/09/07/17-fractals-in-nature/
4.                   Пайтген Х.О., Рихтер П.Х. Красота фракталов. –М.: «Мир», 1993.
5.                   Федер Е. Фрактали. – М: «Мир», 1991.
6.                   [Електронний ресурс]: / Режим доступу: http://ru.wikipedia.org/wikiФрактал.