Дослідницька робота на уроці алгебри у 8 класі.

Вчитель: Ласкіна С.М

 

Тема:  Рівняння, що зводяться до квадратних

Мета: Розширити знання учнів про рівняння. Навчити основним методам розв’язування рівнянь, що зводяться до квадратних. Розвивати логічне мислення, вміння аналізувати, порівнювати, бачити аналогію задач.

                   Завдання групам:

(Всі розв’язані рівняння записуються на дошці.)

 

Група1                                  Розв’язати рівняння

(середній рівень)          1)  х⁴+6х²-7=0

2. (х²-5х)²+10(х²-5х)+24=0

Заміна   х²-5х=у

Група2                                

(середній рівень)          1)   х⁶-3х³+2=0    (заміна х³=t)

2. (х²+1)²-3(х²+1)+2=0

Заміна  х²+1=t

Група3

(достатній рівень)         1)           

Розв’язок

Заміна  

              

              

               

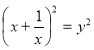
у²-2-2у-1=0

у²-2у-3=0

2) х⁴-2х³-х²-2х+1=0

Ідея: Учні повинні додуматися поділити дане  

          рівняння на х².

         

          

 

          Групуємо доданки

         

          Отримали перше рівняння

Група4

(достатній урівень)            1)(х²+х+1) (х²+х+2)=12

                                                       Розв’язок

                                              Заміна: х²+х+1=у

                                                            у*(у+1)=12

                                              2) х(х+1)(х-1)(х+2)=24

                                                  (х²+х)(х²+х-2)=24

                                              Заміна    х²+х=у

                                                    у*(у-2)=24

Група5

(сильні учні)                        1) 2(х²+х+1)²-7(х-1)²=13(х³-1)

                                                        Розв’язок

                                              2)(х²+ х+1)²-7(х-1)²=13(х-1)(х²+х+1)

                       Поділити обидві частини на (х-1)( х²+х+1)

                                

Заміна      

 

Група6

(сильні учні)                     1) (х²+14х+24)(х²+11х+24)=4х²

                                                           Розв’язок

                                           Поділити на х²

                                           

                                            

                                                           Заміна:

                                              (у+14)(у+11)=4

Група7

(сильні учні)                      1)

                                                            Заміна:

                                                            у=7-х

                                                           

                                                             у⁴+6у²-7=0

 

                              Висновки

1. Рівняння виду:

             

                   Заміна:    

                                    

2. Рівняння виду:

             (x-a)(x-b)(x-c)(x-d)=A

3. Рівняння виду:

                  (x-a)(x-b)(x-c)(x-d)=Ax²

                                Якщо ab=cd

                   Заміна:    

4. Рівняння виду:

             

                   Заміна:     

 

 

 

    Додаткові завдання

1. х⁸-17х⁴+16=0
2. х⁴-4х²-1=0
3. 2х⁴+х³-11х²+х+2=0     (поділити на х²)
4. х⁴-2х³-13х²+14х+24=0
5. х²(х-1)²+х(х²-1)=2(х+1)²
6. (х+3)⁴+(х+5)⁴=16
7. (х-4)(х-5)(х-6)(х-7)=1680
8. (х-2)⁶+(х-4)⁶=64
9. (х+1)⁵+(х-1)⁵=32х
10.                      2(х-1)²-5(х-1)(х-2)+2(х-2)²=0
11.                      8х⁴+8х³-х-190=0
12.                      15х⁴-4х³-6х²-4х-1=0