Урок з алгебри з теми:" Теорема Вієта"
- Мета запропонованої дослідницької роботи допомогти учням “відкрити” теорему Вієта. Вчити учнів бачити аналогію задач, аналогію теорій.
- Для перевірки отриманих знань учням пропонуються індивідуальні диференційовані самостійні роботи за власним варіантом. ( а- власних варіант, порядковий номер в журналі. )
- Для проведення дослідницьких робіт застосовується технологія групової роботи. Кожній групі пропонуються завдання залежно від рівня складності (середній, достатній, високий )
- Група (4-5учнів) виконує проблемне завдання, яке є елементом загальної проблеми. Після обговорення робляться висновки. Всі учні мають можливість взяти участь в дослідженні з урахуванням власних творчих здібностей.
![]() Дослідницька робота на уроках алгебри у 8 класі.
Дослідницька робота на уроках алгебри у 8 класі.
Вчитель: Ласкіна С.М
Тема: Теорема Вієта
Мета: Вивести теорему Вієта. Формувати уміння застосовувати теорему при розв’язуванні квадратних рівнянь. Розвивати традуктивне мислення.
Завдання групам:
- Розв’ язати квадратні рівняння.
Знайти корені х1; х2.
2. Знайти х1 + х2
х1 * х2
3. Чи можливо, не розв’ язуючи рівняння знайти
х1 + х2
х1 * х2
Група 1 (середній рівень).
- х2 – 6х + 8 = 0
- х2 – 2х - 3 = 0
- х2 – 7х + 12 = 0
Група 2 (середній рівень).
1) х2 + 3х + 2 = 0
2) х2 + 2х - 24 = 0
3) х2 + 6х - 7 = 0
Група 3 (достатній рівень).
- х2 – 2х - 1 = 0
х1 = 1 - ![]()
х2 = 1 + ![]()
х1 + х2 = 2
х1 * х2 = 1 – 2 = -1
- z2 – z – 1 = 0
z1 = ![]()
z2 = ![]()
z1 + z2 = 1
z1 * z2 = -1
Група 4 (достатній рівень).
- х2 – 4х – 1 = 0
х1 = 2 - ![]()
х2 = 2 + ![]()
![]()
х1 + х2 = 4
х1 * х2 = -1
-
х2 -
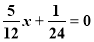
х1 = ![]() ; х2 =
; х2 = ![]()
- у2 + 6у + 5 = 0
Група 5 (високий рівень).
-
х2 +
 х – 1 = 0
х – 1 = 0
- х2 + вх + с = 0
D = в2 – 4с
х1 + х2 = -в
х1 * х2 = ![]()
Група 6 (високий рівень).
1) х2 + ![]() х – 1 = 0
х – 1 = 0
- х2 + рх + q = 0
Висновок:
- Якщо зведене квадратне рівняння має два корені, то їх сума дорівнює другому коефіцієнту рівняння, взятому з протилежним знаком, а добуток - вільному члену.
Це є теорема Вієта.
- Теорема ( обернена до теореми Вієта ).
Якщо сума і добуток чисел m і n дорівнюють відповідно – р і q, то m і n - корені рівняння х2 + рх + q = 0.
3) Цілі розв’ язки рівняння х2 + рх + q = 0 є дільниками числа q.
Завдання за індивідуальними варіантами
а – власний варіант ( порядковий номер у журналі ).
10. Рівняння х2 + рх + q = 0 має корені
х1 = а; х2 = ![]() . Знайти р і q.
. Знайти р і q.
Розв’ язок
Наприклад а = 10 варіант
х1 = 10 ; х2= ![]()
За теоремою Вієта : х1 + х2 = - р
р = - ( 10 + ![]() ) = - 10
) = - 10![]() ,
,
q = х1* х2 = 10*![]() = 1
= 1
х2 - 10![]() х + 1 = 0.
х + 1 = 0.
20. Складіть зведене квадратне рівняння, кореня якого
х1= а; х2= а - 10
Розв’ язок
Наприклад: а = 7 варіант
х1 = 7 ; х2= 7 – 10 = -3
За теоремою Вієта : х1 * х2 = q
q = 7 * (-3) = -21
х1 + х2 = - р
р = - ( 7 – 3) = -4
х2– 4х – 21 = 0
3*. Один з коренів рівняння
х2 – а х + t = 0
х1= а + 3
Знайти : х2 ; t
Розв’ язок
Наприклад а = 20 варіант.
х2 – 20х + t = 0
х1= 23
За теоремою Вієта : х1 + х2 = 20
23 + х2 = 20
х2 = -3
х1 * х2 = t
t = - 23 *3 = - 69.

4*. Знайдіть корені рівняння, q
х2+ 3ах + q = 0, якщо один з них удвічі більше від другого.
х1= 2 х2
Розв’ язок
Наприклад а = 5варіант.
х2 + 15х + q = 0
х1+ х2 = -15
2х2+ х2 = -15
3х2= -15
х2= -5
х1 = -10
q = х1* х2= 50

![]()
5**. Найти суму квадратів коренів рівняння
х2– ах – 1 = 0 не знаходячи х1і х2
Розв’ язок
Наприклад а = 17 варіант.
х2– 17 х – 1 = 0
х1+ х2= ( х1+х2)2 - 2 х1х2= 17 + 2 = 291
За теоремою Вієта : х1 + х2 =17
х 1 * х2 = -1
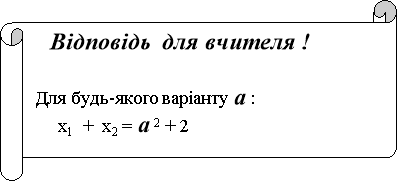
![]()
6***. Найти суму кубів рівняння
х2– ах – 1 = 0 не знаходячи х1і х2
Розв’ язок
Наприклад а = 20 варіант.
х2– 20 х – 1 = 0
х1+ х2= ( х1+х2)( х1 – х1 * х2 + х2 ) = ( х1 + х2 )( ( х1 + х2 )2 – 3х1х2 ) = 20 ( 202 + 3 ) = 8060

1


про публікацію авторської розробки
Додати розробку
