Дослідження "Застосування проблемного навчання на уроках математики"

Застосування проблемного навчання на уроках математики у молодших класах

    Головним напрямком у викладанні математики є виклавдання математики як засобу мислення учнів. Методика викладання випливає з того, що є метою навчання, спирається на вікові особливості учнів та на розуміння причин, що гальмують сприйняття відповідного матеріалу.

  Завдання вчителя полягає насамперед у вихованні учня як активно мислячої особистості, що зможе творчо підійти до матеріалу, який вивчається.

   Зовнішній аспект активної навчальної діяльності школярів полягає в тому, що до цієї діяльності необхідно залучити всіх учнів даного класу і кожного з них.

   Так як до 7–8 років у дітей вже в достатній мірі розвинений план розумових дій, і шляхом навчання за відповідною програмою, в якій властивості математичних структур дані „явно” і дітям даються засоби їх аналізу, можна швидше підвести дітей до рівня „формальних” операцій, ніж в ті терміни, в які це здійснюється при „самостійному” відкритті цих властивостей. При цьому важливо враховувати наступну обставину. Є підстави вважати, що особливості мислення на рівні конкретних операцій до 7–11 років, самі нерозривно пов’язані з формами організації навчання, які є традиційними в початковій школі. Це навчання ведеться на основі гранично-емпіричного змісту, часто взагалі непов’язаного з понятійним (теоретичним) відношенням до об’єкту. Таке навчання підтримує і закріплює у дітей мислення, що спирається на зовнішні, прямим сприйняттям уловимі ознаки речей.

   Дослідження показали, що в процесі розв’язання арифметичних задач і набуття знань з інших навчальних предметів в учнів під керівництвом учителя формуються узагальнені мислительні дії. Прикладом цього є оволодіння учнями алгебраїчними способами розв’язання арифметичних задач, що доведено дослідженнями О.Скрипченка.

   Як показано в низці спеціальних досліджень (Г.Кагальняк, Т.Косма та ін.), розвиток порівнянь у молодших школярів значною мірою залежить від того, наскільки часто даються учням завдання на порівняння різних об’єктів, їх груп і класів, як визначаються орієнтири для зіставлення об’єктів, виділення їх істотних подібних і відмінних ознак. За даними В.Шадрікова, однією з особливостей абстракції в учнів молодших класів є їх тенденція приймати зовнішні, яскраві ознаки об’єкта за суттєві, хоча вони нерідко не є такими. З більшими труднощами діти підводять під поняття дієслова, що означають стани, а ще важчими для них є дієслова з абстрактним значенням .

   Таким чином, проблема розвитку пам’яті і мислення молодшого школяра в процесі провідної (навчальної) діяльності достатньо з’ясована. Проте, оскільки воно недостатньо досліджене експериментально, потребує подальшого вивчення питання розвитку пам’яті та мислення в процесі проблемного навчання та ігрової діяльності.

   Шляхом послідовного ускладнювання задач або питань створюється в мисленні учня така проблемна ситуація, для виходу із якої (для знаходження відповіді) йому не вистачає наявних знань, і він повинен сам активно формувати нові знання за допомогою вчителя  і за участю інших. Таким чином, нові знання учень одержує не в готових формуваннях вчителя, а в результаті власної активної пізнавальної діяльності. Вони є ніби його власним відкриттям, продуктом його власних узагальнень і висновків власної пізнавальної праці. Застосування проблемного навчання призводить до більш глибокого осмислення і прискореного практичного засвоювання знань.

   У процесі викладання математики в початкових класах, учитель спирається як на безпосереднє сприймання учнями окремих предметів або фактів, так і на їхню уяву. У початкових класах вона є засобом здобування учнями чуттєвих даних, необхідних для утворення уявлень і понять про предмети чи явища навколишньої дійсності. За допомогою наочності збагачується, розширюється особистий пізнавальний досвід учнів, розвивається спостережливість.

Отже, використання методу проблемного навчання при вивченні математики у початковій школі сприяє розвитку пізнавальної діяльності молодшого школяра і виявляється в активізації цієї діяльності.

Завдання №1

Тема. Засвоєння таблиці множення числа 8. Розв’язування задач.

Мета: закріпити знання табличних випадків множення і ділення; вдосконалювати вміння розв’язувати задачі, навички усних обчислень; розвивати логічне мислення, увагу; виховувати акуратність.

Обладнання: сигнальні картки, предметні малюнки

Література: Богданович М. В. Математика: підручн. для 2 кл. загальноосвітн. навч. закл./ М. В. Богданович, Г. П. Лишенко. – К.: Генеза, 2012. – 160с.: іл. 

Хід уроку

І. Організаційна частина.

ІІ. Контроль, корекція та закріплення знань учнів.

1. 7 80 75 22 30 50 10 4

1. Прочитай числа в порядку зростання.
2. Прочитай числа в порядку спадання.
3. Вибери із переліку круглі числа. Назви їх.
4. Назви тільки двоцифрові числа. Тільки одноцифрові.

2. Гра «Підтверди або спростуй» (робота на дошці)

1. (50+6):8=5
2. (45-13):4=8
3. 6∙8-24=24
4. 4∙3+48=70
5. 8∙(30-26)=40
6. 5+(40:8)=10
7. 48:8-6=1

3)   Математичний диктант.

1. Добуток чисел 7 і 5 зменшити на 15.

2. Різницю чисел 50 і 8 зменшити у 7 разів.

3. Суму чисел 56 і 7 зменшити у 7 разів.

4. Частку чисел 35 і 7 збільшити на 95.

5. Добуток чисел 7 і 3 зменшити на 17.

6. Різницю чисел 40 і 26 зменшити у 2 рази.

7. Частку чисел 42 і 7 збільшити на 34.

8. Суму чисел 27 і 29 зменшити  у 7 разів.

4)) Гра «Вірю – не вірю»

- Зараз я читатиму твердження і якщо воно вірне, то ви будете плескати в долоні, а якщо ні, то хитатимете головою.

1. Сума більша за будь-який доданок. (Так)

2. Числа при діленні називаються доданок, доданок, сума. (Ні)

3. Зменшуване завжди більше за від’ємник. (Так)

4. Числа при додаванні називаються доданок, доданок, сума. (Так)

5. Знайти добуток чисел означає два числа відняти. (Ні)

ІІІ. Повідомлення теми і мети уроку.

• Сьогодні на уроці ми будемо повторювати вивчені таблиці множення і ділення та розв’язувати задачі.

IV. Повторення вивченого матеріалу.

1. Робота з підручником. №883

               Встав пропущені числа.

 *:3=6

*∙5=30

*:5=4

*-7=42

*:7=2

*∙6=48

2. Робота над задачею. (проблемне завдання)

Сливи розклали порівно в 7 ящиків. А яблуків в одному ящику – 12 кг. У скільки разів  менша маса слив у ящику, ніж яблук?

(діти говорять, що не можуть дати відповідь на запитання задачі, оскільки не достатньо даних. Для того, щоб відповісти потрібно знати скільки кілограм слив було в одному ящику.)

• Отже, що потрібно змінити в задачі, щоб можна було її розв’язати? (Потрібно додати масу слив в одному ящику)
• Додайте необхідні дані і розв’яжіть задачу. (Колективно учні додають дані і самостійно розв’язують задачу)
•  

3. Робота з підручником №885 (розв’язування кругових прикладів)
4. Фізкультхвилинка

• А тепер у нас розминка,
  А тепер фізкультхвилинка.
  Встали рівно біля парт,
  Починаємо наш старт.
  Ось зігнули так ручата
  Й полетіли, мов качата.
  Ніжками затупотіли,
  Потім разом всі присіли.
  До сонечка потяглися
  І у боки так взялися.
  Вправо разом нахилились,
  Вліво, щоб не помилились.
  Руки вниз ми опустили
  Й трохи ними потрусили.
  Шию трішки розім'яли
  І за парти посідали.
  А тепер мерщій до справ,
  Кожен вченим з нас щоб став.

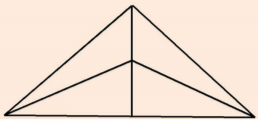
5. Полічи на малюнку трикутники

V. Узагальнення й систематизація знань учнів.

1)   Дії з іменованими числами ( постановка проблемної ситуації):

- В яких одиницях вимірюється маса?

Вирази в кг:

2 ц = ___ кг

9 ц = ____кг

3 ц 3 кг = ____ кг

9 ц 3 кг = ___ кг

Вирази в ц:

500 кг =____ц 

6 т =____ ц 

340 кг = ___ц ___кг 

759 кг = __ ц ____кг

- Порівняйте: ( постановка проблемної ситуації)

5 кг * 5 ц

20 ц * 200 кг 

4 т * 400 ц                

34 кг * 8 ц

- Можна порівнювати різні одиниці маси?

- Що необхідно зробити перед тим, як поставити знаки порівняння?

2) Робота над задачею №887

        У шкільному хорі 24 дівчинки, а хлопчиків – у 3 рази менше. Скільки всього дітей у хорі?

• Збільш кожне число в задачі у 2 рази. Як від цього зміниться відповідь?

3. Робота над задачею (самостійно)

На першій ділянці посадили  8 кущів смородини та 7 кущів малини, на другій – у 2 рази більше смородини, ніж на першій та 5 кущів малини. Скільки всього кущів  смородини посадили на двох ділянках? (Учні використовують лише дані, що стосуються кущів смородини і доходять висновку, що в задачі є зайві дані.)

VI. Підведення підсумків уроку

1. Гра «Мікрофон»

• Я навчився…
• Я дізнався…
• Найбільше мені сподобалося…
• Важким для мене було…

VII. Домашнє завдання

   С 133 завдання №890, 891

Завдання №2

1. Створення проблемної ситуації

• Діти, чи знаєте ви, що на Олімпійських іграх плавці пливуть по 200 метрів. Звичайно, для пересічної людини така дистанція є важкою і тому вона буде пропливати цю дистанцію із перервами.

2. Постановка проблеми

• Отже, сьогодні на уроці ми повинні порахувати скільки кіл вздовж басейну потрібно зробити плавцю, щоб проплисти 200 м.

3. Висунення гіпотези

• Для того, щоб знати скільки підходів може зробити людина, варто знати яку максимальну відстань вона може проплисти за 1 раз. За 1 підхід людина може проплисти 50 метрів. Також нам відомо, що довжина басейну – 15 м, а ширина – 10 м.

4. Розв’язання проблеми

• Що нам потрібно мати, щоб дізнатися скільки кіл може проплисти людина? (Довжину одного кола)
• Що ми можемо дізнатися з даних, які відомі? (Периметр басейну, що і буде довжиною одного кола, оскільки плавець пливе вздовж краю басейну)
• Яка довжина одного кола? ( 50 м)
• Що означає це число? (Кількість метрів, які може проплисти людина за один підхід)
• Отже, яка буде мірка виміру? (Одне коло басейну)
• Скільки кіл потрібно зробити плавцю? (200:50=4 кола)

5. Формулювання висновку

• Оскільки одне коло має довжину 50 метрів, то плавцеві слід зробити 4 кола, щоб проплисти олімпійську дистанцію.

Завдання №3

1)

         =       

        >

       ?

2)

           +     +    =

     -     =     +?

    =       -?-?

     =?-?-?