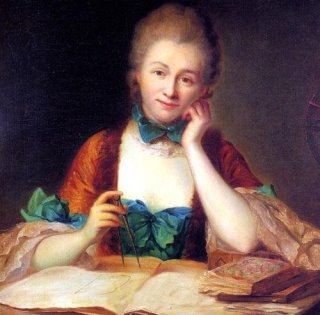Науково-дослідницький проект "Жінки в математиці"

Вендичанська СЗШ І-ІІІ ступенів, гімназія

 

 

 

 

 

Науково-дослідницький проект:

«Жінки в математиці»

 

 

 

 

 

 

 

Підготувала Буланюк О.С.

 

 

 

 

 

 

 

 

Лютий, 2014р.

 

Зміст

 

І. Вступ

ІІ.  Давньогрецькі математики

1. Гіпатія
2. Феано

ІІІ. Італійські математики

3. Аньєзі Марія Гаетана
4. Елена Лукреція Корнаро Піскопія

ІV. Французькі математики

5. Емілі дю Шатле
6. Софі Жермен

V. Російські математики

7. Софія Ковалевська

VI. Німецькі математики

8. Еммі Нетер
9. Ада Байрон

VIІ. Українські математики

10.                    Ольга Олійник
11.                    Катерина Ющенко
12.                    Галина Матвієвська
13.                    Олена Дубинчук

VIII. Висновки

ІХ. Додатки

Х. Використана  література

 

 

 

 

 

 

 

 

Мета:

- розширити знання учнів про видатних математиків; розвивати пізнавальний інтерес; виховувати прагнення до безперервного вдосконалення своїх знань; показати необхідність знань з математики в житті кожної людини; 

- розвивати навики роботи з різними видами літератури, вміння проводити пошукову роботу ;

- сприяти розвитку ініціативності та комунікативних навиків;

 

 

Завдання проекту:

 Розширити знання учнів про видатних жінок в математиці; дослідити їх життєвий та творчий шлях;

показати згуртованість та вміння донести до оточуючих необхідний матеріал.

 

Основні питання:

           Ключове питання:

Який цікаві факти з життя   видатних жінок математиків відомі світові?

           Тематичні питання:

Що відомо про внесок в математичну науку жінок-математиків?

Як проявилися перші математичні здібності в юних математиків?

Що відомо про особисте життя відомих жінок - математиків?

Які найбільші відкриття їх нам відомі?

 

Очікуванні результати:

• Підвищити інтерес учнів до вивчення математики;
• Поглибити розуміння учнями математичного матеріалу;
• Розширити розумовий кругозір учнів і підвищити їх загальну культуру;
• Створити в учнів правильний погляд на математику в цілому.

 

 

Стислий опис:

Математика – велика складова частина   загальнолюдської культури, а історія математики  є частиною історії культури. Тому завдання вчителя познайомити учнів з  фактами культурного життя людства, продемонструвати тернистий шлях вчених, а саме жінок та їх теорій.

 

Математика – надзвичайно важлива наука.                                           Видатних математиків, які розвивають цю науку, відомо багато. Почесне місце серед них посідають жінки. Вони створили наукові праці та підручники, які збагатили скарбницю світової математичної літератури.

Учасники проекту:

 

10-А	10-Б
Тимошенко Віталій Матієк Станіслав Кізян Анастасія Чорна Наталія Поліщук Яна Слободянюк Катерина Дручок Анатолій Мельник Андрій Садикін Олександр	Невмержицький Максим Барабаш Вадим Мельник Олександр Левурдяк Олена Кухаренко Олег Любарець Вадим Дужий Владислав Фаста Вікторія

Форми роботи:

 Розподіл завданнь,  пошукову роботу, обробка зібраного матеріалу, підготовка виступів та мультимедійних презентацій.

 

 

 

 

 

 

ГІПАТІЯ

Гіпатія (Іпатія) з Александрії (грец. Ὑπᾰτία ἡ Ἀλεξάνδρεῖα) (*370 — †415) — філософ, математик і астроном. Дочка александрійського математика Теона. Послідовниця неоплатонівської школи Ямвліха. Займалася обчисленням астрономічних таблиць, написала коментар до твору Аполлонія (щодо конічних перетинів) і Діофанта (з арифметики), які не збереглися. Гіпатія брала участь у громадських справах міста і користувалася значною популярністю.

Гипатія Александрійська – видна представниця старогрецької філософії і математики. Гипатія, по опису істориків, була жінкою незвичайної краси і больщого розуму. Батько Гепатії – Теон Александрійський, крупний учений-математик, що написав тлумачення до астрономічного твору Птолемея і на знамениті геометричні “Початки” Евкліда.

Гіпатія була дочкою александрійського філософа та математика Теона. Мати її вмерла при пологах, і дівчинка жила з батьком в Александрійському мусейоні. Батько навчив її ораторському мистецтву та вмінню переконувати людей. Він працював в Александрійському мусейоні. Александрійський мусейон являв собою великий науковий центр того часу. Найвідоміша у наш час александрійська бібліотека і зараз має світову славу. На той час вона становила лише частину музею, доскладу якого також входили організації за сучасним уявленням порівняні з Академією наук та університетом. Саме там Іпатія отримала свою першу освіту. Далі вона навчалася у Афінах. Історія людства знає лише два міста, вплив яких на розвиток культури суспільства неможливо переоцінити — це  Спарта  та Афіни. Перше прославилося патріотизмом, а друге — високим рівнем культури.

В Афінах Гіпатія вивчала праці Платона  та  Аристотеля. А потім, повернувшись до  Александрії, починає викладати в Мусейоні математику, механіку, астрономію та філософію.

  Гіпатія опинилася у центрі війни релігій. Час її життя припадав на самий кінець античного світу. Люди античності були язичниками. За Костянтина християнство стало панівною релігією. Язичники та їх культура жорстоко переслідувалися. Для християн у ті часи будь-які знання, крім догматів та віри, були незрозумілі. Нещадно знищувалися цінності античної культури. Так у 391 році за наказом єпископа Феофіла було знищено александрійський храм Серапейон з усім книжковим скарбом. У 394 роціімператор Феодосій, який отримав від християнської церкви прізвисько «Великий», скасував Олімпійські ігри, порушивши давню традицію греків. Багато античних храмів, пам'яток великої стародавньої культури, було зруйновано.

На початку V сторіччя астрономія була частиною математики, а різниці між астрономом, який вивчає небесні явища, і астрологом, який передрікає долю за зірками, не робилося. Навіть в офіційних документах звіздарів називали просто математиками. У 409 році імператори Гонорій і Феодосій II видали спеціальний закон. Математикам ставилося в обов'язок з'явитися до єпископа, відректися від богопротивних поглядів, спалити список своїх помилок і присягнути дотримуватися християнської віри. Тих же, хто відмовлявся принести зречення, необхідно було вигнати з Риму та всіх інших міст. Математиків, які наважилися порушити цю постанову, самовільно залишилися в містах або під прикриттям неправдивої присяги продовжували потай займатися своєю професією, належало карати без усякого милосердя.

Впливовість Гіпатії не подобалася духовенству, оскільки вона викладала філософію язичників — вчення              неоплатоніків.   Александрійський патріарх (412–444 років)               Кирило проводив жорстку політику утвердженняхристиянства. Він був ворогом Гіпатії та поширював плітки про те, що Гіпатія чаклунка. Пізніше було знайдено привід для страти. Був вбитий якийсь монах на ім'я Гієрака. Кирило звинуватив Гіпатію в причетності до вбивства. Це спричинило істерику серед християн. У 415 році під час березневого посту натовп релігіозних фанатиків під керівництвом Петра звірськи забив жінку. Натовп витягнув Гіпатію з ношів, її побили та затягли до християнського храму. Тут з неї зірвали одяг та порізали гострими кінцями раковин. Тіло її було розірване на шматки, а залишки спалили у вогні. Так за свою мудрість та красу сплатила Гіпатія страшну ціну. За життя Гіпатії її сучасник та земляк, поет Феон Александрійський присвятив їй теплу епіграму:

«Коли ти переді мною я чую твою мову,

Благий твій погляд та обитель зірок чистих
Я підношу, — так все в тобі , Іпатіє,
Небесне — і справи, і краса промов,

І чисте, як зірки, науки мудрої світло».

Іпатія була останнім представником давньогрецької математики. «Після цих останніх спалахів вогню грецької математики загасло, як загасла свічка» , — писав Ван дер Варден у книзі «Пробудилася наука». Але пам'ять про Іпатію залишилася назавжди. Її наслідують багато вчених сучасності. У 20 сторіччі ім'ям Іпатії назвали один з кратерів Місяця.

В історії науки Гіпатія відома як винахідник. Вона створила такі астрономічні прилади: пласка астролябія — прилад для визначення широт і довгот в астрономії, яка використовувалася для визначення знаходження Сонця, зірок та планет, а також планісферу — зображення небесної сфери на площині, на якій можна обчислювати захід і схід небесних світил. Гіпатія винайшла  ареометр — прилад для визначення густини  рідини.

Гіпатія обчислювала астрономічні таблиці, написала коментарі до наукових творів Аполлонія та Діофанта.

Вона мала славу талановитого вченого та викладача. До Гіпатії в Александрію приїжджали вчитися люди з різних країв світу. Одним з її учнів був Синезій, єпископ Птолемаїди.

Утворення Гипатія отримала під керівництвом свого батька, що належав до учених Александрійської школи. Гипатія, крім математики, займалася також філософією і астрономією. Її твори до нас не дійшли. Але добре відомо, що Гипатія написала грунтовні коментарі по теорії конічних перетинів Аполлонія Пергського і на твори алгебри Діофанта Александрійського. Крім того, нею складений ряд робіт по філософії і астрономії. Стверджують, що Гипатії належить честь винаходу ареометра – приладу для визначення щільності рідини, астролябії – приладу для визначення широт і довгот в астрономії – і планісфери – зображення небесної сфери на площині, по якому можна обчислювати схід і захід небесних світил.Близько 400 року Гипатія була запрошена читати лекції в знамениту Александрійську школу. Вона зайняла кафедру філософії, одну з провідних кафедр школи. Лекції вона читала при великому збігу слухачів. Слава про неї рознеслася далеко за межі Александрії. Свої лекції Гипатія зазвичай починала з викладу вибраних питань математики, потім переходила до її додатків і інших наук, сукупність яких складала стародавню філософію. На уклін до жінки – філософові і математикові зі всіх кінців Римської імперії стікалися учені, щоб залучитися до джерела краси і розуму.Ця популярність язичника Гипатії, що росте в народі, не подобалася архієпископові Кирилу, і він вирішив знищити її. Кирило нацькував на Гипатію ченців і ті, подкораулів її біля будинку, накинулися на Гипатію і поволочили її в церкву. Там, під покровом розіпнутого Христа, роздерши в клапті весь одяг, нещасний знівечили уламками черепиці і битих судин. Потім тіло мучениці волочили по вулицях Александрії. Коли поривши сказ натовпу небагато утихнув, тіло Гипатії було розрубане на шматки і спалене на багатті.Із загибеллю Гипатії Александрійською фактично закотилося сонце старогрецької математики. Гипатія була її останньою представницею. “Після цих останніх спалахів полум'я грецької математики згасло, як догоріла свічка”, - писав Ван дер Варден в книзі наука, що “Прокидалася”.

Гіпатія внесла свій внесок у геометрію і астрометрію, крім того, зіграла важливу роль у створенні астролябії. "Зберігай своє право на думку, мислити неправильно краще, ніж не думати зовсім", говорила Гіпатія.

Противники Гіпатії вбили не тільки її. Їм вдалося знищити і спадщину великої Жінки - не залишилося жодного запису, зробленого Нею. Тобто, вбита була і сама пам'ять про Теона. Лише за збереженими спогадами сучасників змогли вчені відновити її біографію. Багато століть по тому про Гіпатію напишуть наукові праці та романи, назвуть її двічі вбитою. Гіпатії присвячено багато віршів.

Гордість народу, серце і мрія:
В числах відчула музику,
Давній астроном Александрії –
Вченого світу Муза!

Вогнем спопелили Гіпатію
Мудру красуню безвинну,
Вченого світу симпатію,
Генія розум єдиний!

Після смерті Гіпатії Александрійської протягом 1000 років в історії математики ми не зустрічаємо імен жінок.

 

ФЕАНО

Перше ім’я жінки, яке зустрічається в історії математики, це Феано (Теано) - учениця і дружина давньогрецького філософа, великого математика і мудреця - Піфагора, який жив у VI - V ст. до н.е.

Після повернення зі своїх мандрівок Піфагор заснував школу або, як її часто називають, університет в Кротоні, дорійської колонії  на Південі Італії. Спочатку у Кротоне на нього дивилися скоса, але через деякий час можновладці в цьому місті вже шукали його порад в справах величезної важливості. Він зібрав навколо себе невелику групу відданих учнів, яких посвятив у глибоку мудрість, йому відкриту, а також в основи окультної математики, музики, астрономії, які розглядалися їм як трикутна підстава для всіх мистецтв і наук.

У віці 60 років Піфагор одружився на своїй учениці Феано, дівчині дивовижної краси, яка підкорила серце мудрого філософа своєї чистої і полум'яною любов'ю, безмежною відданістю і вірою.

   Відомо, що вона була найважливішим слухачем у школі Піфагора. Про це свідчить задача з Палатинської антології – найвідоміші збірки Х-ХІVст., проте запитаємо самого Піфагора.

- Скажи мені, знаменитий Піфагор, – скільки учнів відвідують твою школу і слухають твої бесіди?

- Половина з них вивчають математику, четверта частина – музику, сьома частина мовчить і, крім того, є ще жінки.

Злиття цих двох життів виявилося досконалим. Феано перейнялася ідеями чоловіка з такою повнотою, що після його смерті вона стала центром пифагорейского ордена, і один з грецьких авторів призводить, як авторитет, її думки стосовно вчення Чисел. (Е. Шюре.Великі Посвячені)

Сім'я Піфагора представляла собою справжній зразок для всього ордена, його будинок називали храмом Церери, а двір - храмом Муз.

Феано народила Піфагору двох синів і дочку, всі вони були вірними послідовниками свого Великого батька. Один з синів Піфагора став згодом вчителем Емпідокла і познайомив його в таємниці піфагорійського навчання. Дочки своєї Дано Піфагор довірив зберігання своїх рукописів. Після смерті батька і розпаду союзу Дано жила в найбільшої бідності, їй пропонували великі суми за манускрипти, але вірна волі батька, вона відмовилася віддати їх в сторонні руки.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

АНЬЄЗІ МАРІЯ ГАЕТАНА

(1718 – 1799)

 

Марія Аньезі народилася в Мілані 16 травня 1718 в родині заможного буржуа , дворянина і , може бути , - професора Болонського університету Петра Аньезі . Сім'я мала 21 -го дитини ( від трьох дружин П'єтро Аньезі ) , і Марія була старшою з них .

    З дитинства вона виявляла неабиякі таланти в пізнанні мов і філософії. У дев'ятирічному віці Марія написала латинський трактат , де захищала право жінок на освіту. У науковому салоні свого батька з 13 років вона робила філософські доповіді на 7 мовах , стародавніх , східних і європейських. Математиці вона вчилася у Раміро Рампінельі , римського і болонського професора математики.

    Коли в 1732 році померла її мати , перша дружина П'єтроАньезі , Марія стала дуже релігійною , і навіть просила батька відправити її в монастир. Батько не погоджувався , пишаючись здібностями своєї дочки , і нічого не шкодував для її подальшого наукового розвитку . У власній міланської друкарні він друкував всі твори , написані Марією.

    Першу роботу «Філософські судження» ( PropositionesPhilosophicae , 1738 ) Марія опублікувала в 20 -ти річному віці. У 30-річному надрукувала «Основи аналізу» ( Istitutionianalitiche ) на італійській мові , що містили понад 1000 сторінок. Цю книгу Марія Аньезі писала майже 10 років як підручник для своїх молодших братів і сестер , і там викладалися всі розділи математики початку XVIII століття. Ця праця користувався славою і перекладався багатьма мовами аж до початку XIX століття , будучи схвалений Французької Академією Наук і римським папою Бенедиктом XIV (1740-1758) , який в 1750 році дав їй кафедру математики в Болонському університеті. Невідомо - викладала чи Марія Аньезі в цьому університеті або її посаду професора мала почесний характер. Крім чистої математики , Марія займалася ботанікою , мінералогією , астрономією , богослов'ям . Після смерті батька в 1752 році М. Аньезі віддалилася від світських занять , ставши настоятелькою міланської богадільні .

    Останні роки життя Марії Аньезі відомі менш достовірно . Історики погоджуються з тим , що вона померла в 1799 році. Однак дати її кончини вказуються різному : 9 cічня або 4 серпня.  За спогадами бачили її сучасників , в молодості Марія Аньезі була особливо красива , але володіла миловидністю , а коли починала розмірковувати на наукові теми , ставала схожа на ангела своєю чистотою і розсудливістю .

    Марія Аньезі завжди була вірною католичкою . У « Філософських судженнях » ( PropositionesPhilosophicae ) , написаних нею в 20 -ти річному віці , вона дотримується поглядів французького ченця і філософа Миколи Мальбранша ( 1638-1715 ) , пристосувавши вчення Декарта до церковних догматам . У цій системі наука має апологетичний сенс і розділяється на дисципліни , що містять абсолютну істину - геометрію і арифметику , та інші емпіричні дисципліни , що вже мають відносну і умовну природу - механіку , фізику , астрономію. У своїх «судження » Марія Аньезі захищала 191 філософський тезу.

    Слідом за Мальбраншем Аньезі вважала , що наука і релігія не можуть суперечити один одному , а метою науки є вивчення зв'язку між ідеями і речами.

  Слід припускати , що католицьким вченим XVIII століття було нелегко пристосувати свої знання до вимог Церкви та її інквізиції , і саме тому вони уникали займатися астрономією , механікою і фізикою . Адже праця Коперника « Про обертання небесних сфер» був засуджений католицькою церквою і занесений в Індекс заборонених книг аж до 1835 року. А реформовані версії системи Птолемея не задовольняли законам фізики , відкритим Галілеєм і Ньютоном . Під цим кутом зору слід розглядати і математичні роботи Марії Аньезі . У 17 років Марія вивчила працю Гійома Лопиталя ( 1661-1704 ) «Про конічних перетинах » ( Traitéanalytiquedessectionsconiques , 1707 ) і написала коментарі до нього . Вона ознайомилася з його основною роботою « Аналіз нескінченно малих» ( Analysedesinfinimentpetits , 1696 ) , освоїла « Аналіз» ( AnalysedémontréeouManièrederesoudrelesproblèmesdemathématiques , 1708 ) Шарля Рейно ( 1656-1728 ) , праці італійських математиків Гвідо Гранди (1671-1742) і Габріеля Манфреді ( 1681-1761 ) .

    Нібито , з метою полегшення викладання математики молодшим братам і сестрам , Марія Аньезі взялася за систематизацію математичного аналізу , який в ту пору був роздирають науковими суперечками між послідовниками Ньютона і його методу флюксий і прихильниками диференціального методу Лейбніца . Ньютоніанци домінували у Великобританії і почасти - у Франції , лейбніціанца було більше в Швейцарії і Північної Італії. Всупереч цьому географічному розкладу , Марія Аньезі була ньютоніанкой , але при цьому була добре знайома і з методами Лейбніца , які послідовно використовувала у своїх роботах. У своїй праці «Основи аналізу» , який вона писала з 1738 по 1748 рік, Марія об'єднала обидва підходи , справедливо зауваживши , що між ними немає істотної різниці. При написанні цієї книги Марія Аньезі зустріла підтримку і дружні поради з боку італійських математиків Риккати .

    «Основи аналізу» написані італійською мовою і складалися з двох томів загальним обсягом понад тисяча сторінок. У першому томі ( 1748 ) дані геометричні методи Декарта і теорія алгебраїчних рівнянь . У другому томі ( 1749 ) систематично викладена теорія диференціального й інтегрального числення . Підхід до викладу геометричний , як в « Принципах » Ньютона , але ніякі прикладні (механічні , фізичні чи астрономічні ) завдання не ставляться і не вирішуються.

    Книга М. Аньезі виявилася першим систематичним викладом всієї математики XVII - початку XVIII століть , чим привернула увагу всього світу вченого . Десять примірників книги , посланих до Французької Академії Наук , були прийняті з захопленням , книгу називали найбільш повним підручником з математики . Римський папа , реформатор і просвітитель Бенедикт XIV (1740-1758) , колишній Великий інквізитор Риму , в 1750 році призначив Марію Аньезі професором кафедри математики нововідкритого жіночого факультету Болонського університету.

    Невідомо - чи працювала М. Аньезі в університеті. Мабуть , належачи до багатого сімейства , в грошах вона не потребувала , а незабаром , після смерті батька в 1752 році , Марія віддалилася в міланський монастир , ставши настоятелькою тамтешньої богадільні .

Підручник « Основ аналізу» Аньезі користувався популярністю аж до початку XIX століття. Джон Кольсон в середині XVIII століття перевів його на англійську мову , змінивши диференціальні позначення Лейбніца на ньютоніанскогофлюксии . Цей переклад був опублікований в 1801 році.

  У математиці є спеціальна крива третього порядку , звана по-російськи « локон Аньезі » , а по-латиною « завиток Аньезі » ( versoria - канат для повороту вітрила ) . По-англійськи ця крива називається « відьмою Аньезі » ( witchofAgnesi ) , припускають - через те , що Джон Кольсон не впорався з перекладом рідкісного італійського слова « laversiera ».

 

 

 

 

 

 

 

Елена Лукреція Корнаро Піскопія

Елена Лукреція Корнаро Піскопія (італ. Elena Lucrezia Cornaro Piscopia; 25 червня (за іншими даними 5 червня) 1646, Венеція —26 липня 1684, Венеція) — італійська філософиня, математик, перша жінка у світі, яка здобула докторський ступінь.

Піскопія була дочкою прокуратора Венеції. Здобула добру освіту, зокрема опанувала декілька сучасних і класичних мов та «вільні мистецтва». Вона зневажала фривольність венеціанського суспільства й ще замолоду пішла в черниці до бенедиктинок. Піскопія з часом вирішила повністю присятити себе науці. У 1677 році вона провела свій перший публічний диспут в Падуанському університеті. Спроби батька організувати для дочки докторський титул спершу закінчилися невдачею. Опоненти вважали, що місце жінки в церкві, де вона має мовчати, тож викладати жінці не пасує. Та врешті Піскопія добилася дозволу захистити докторську дисертацію. 25 червня 1678 року вона стала першою жінкою у світі, яка здобула звання доктора наук.

Наступні шість років вона займалася виключно науковою роботою, зокрема на теренах філософії і математики. Померла у віці 38 років, як припускають, від раку. У 1688 році її науковий доробок був опублікований в Пармі.

 

 

 ЕМІЛІ, МАРКІЗА ДЮ ШАТЛЕ

(1706 - 1749)

Життя Емілі де Бретейль, маркізи де Шатле викликає подив у багатьох відношеннях. Вона народилася у 18-му столітті в епоху французького дворянства, її ім'я було пов'язано з іменами Лейбніца, Ньютона і Вольтера. Емілі прожила 43 роки. Озираючись назад, можна сказати, що її незвичайне життя було цілком природне для неї.

Габріель-Емілія ле Тоннел'є де Бретейль народилася в Парижі 17 грудня 1706.

Її батько Ніколя Луї Тоннел'є де Бретейль, був головним секретарем і послом Людовика XIV. Ця посада помістила його в центр суспільного життя і створила йому і його родині високий статус і повагу. Її мати, Габріель Анн де Фролан, виховувалася в монастирі.

Можливості отримати освіту для дівчаток в цей час були обмежені: або в монастирі, або в школі, або вдома. Брюс навчалася вдома і отримала відносно гарну освіту. У неї були великі здібності до наук, які вона проявила, не дивлячись на юний вік. Це переконало її батька, що ця дівчинка заслуговує уваги. Вона обіцяла вирости дуже красивою, а викладачі та гувернантки займалися розвитком її інтелекту.

Вона була напрочуд добре освічена і до 12 років вільно спілкувалася латиною, італійською, грецькою і німецькою мовами. Вона здобула освіту в галузі математики, літератури і науки. Вона так само любила танцювати, була чудовою виконавицею вокалу, співала оперу, і виступала як актриса в аматорських виставах. Вона вивчила Вергілія, Тассо, Мільтона, Горація і Цицерона.Але її істинною любов'ю була математика.

Досягнувши юності, Емілі стала красивою і незалежною, з сильним і пристрасним характером.Вона реально оцінювала свої перспективи на вступ у шлюб. Їй хотілося б знайти чоловіка, який дозволив би їй бути незалежною і повністю реалізувати свої інтереси і нахили. Вона вирішила, що знайде це в шлюбі з Флораном - Клодом, маркізом дю Шатле, графом Лаумонт. Вони уклали шлюб 20 червня в 1725 році, коли Брюсові було 19 років.

Вона стала маркізою де Chastellet (правопис Châtelet був введений Вольтером і став стандартним). Шлюб був укладений не з любові, а з розрахунку і подружжя не мало ічого спільного між собою, що було характерно для того часу.

Маркіз був військовою людиною і губернатором. Він проводив багато часу зі своїми солдатами.Добродушна, обмежена людина, любляча військову службу, полювання і нічого більше, він нікому не заважав і нікого не цікавив.

Емілія Дю Шатле була зовсім іншою людиною. Ще в будинку батька вона вивчила латинську мову і грунтовно ознайомилася з римськими класиками. Пізніше вона пристрастилася до математики та метафізики. І це був не дилетантський інтерес до наук, значно поширений серед освічених жінок XVIII століття. Маркіза дю Шатле трудиться наполегливо, серйозно й уважно, викладає Лейбніца і переводить Ньютона.

Думка сучасників і, особливо, сучасниць лестить Емілі. Ось думка дами, пані дю Деффан:«уявіть собі жінку високу і суху, з різкими рисами обличчя і загостреним носом - ось фізіономія прекрасної Емілії, якою вона так задоволена, що не шкодує зусиль, змушуючи милуватися собою. Вона бажає здаватися гарною наперекір природі і багатою, наперекір своєму скромному статку». Дама явно Емілії не симпатизує.

А ось що каже чоловік, сучасник, Гюстав Лансон: «Вона мислила». І ще: «Її вважали педанткой, але вона була щиро-серйозна. Вона писала наукові та філософські теми.Вона володіла чоловічим розумом і чоловічим серцем: пряма, вірна, вона була здатна на самопожертву: вона була набагато краще тих жінок, які нерідко насміхалися над нею і лихословили про неї».

В 1733 році починається її дружба з Вольтером, який залишиться з нею на все життя. З 1732 по 1748 рр.. ці яскраві, внутрішньо неприборкані особистості співіснували в особливому, створеному ними світі, де духовне поєднувалося з пристрасною закоханістю. Вони належать один одному душею і тілом обом здається, що вони люблять в перший раз. Маркіз дю Шатле добродушно поглядав на нову прихильність своєї дружини.

У відносинах Вольтера і маркізи дю Шатле химерно перепліталися любов, наука, література. Ще в 1733 році Вольтер жартівливо писав:

Ее широкий ум все ценит с равным рвеньем:
Писанья, бириби, поклонников, бокал,
Алмазы, оптику, поэзию, помпоны,
Наряды, алгебру, Горация, хорал,
Обеды, физику, суды и котильоны.

                    (Переклад А. Кочеткова)

Вольтер дійсно любить її інакше, ніж своїх колишніх коханих. З любов'ю до неї у нього з'єднуються глибока повага, захоплення її розумом і характером. Це не тільки любов, але разом і розумове товариство. На самому початку їхнього союзу Вольтер поспішає поділитися з Емілією своїми знаннями та інтересами. Він перечитує з нею своїх улюблених англійських філософів і поетів: Ньютона, Локка, Поупа. Де в чому вони були рівні і могли бути товаришами, у неї не було, звичайно, і сотої частки його таланту, його різнобічності. Але пізнаннями у деяких галузях природничих наук і у вищій математиці, вивченої нею під керівництвом кращих фахівців того часу, вона перевершувала свого друга.

У 1734 році Вольтер і Емілі оселилися в замку Сірей-сюр-Блаз на кордоні Лотарингії і Шампані. У якому, як вони думали, Вольтер міг би уникнути переслідування. Замок був оброблений заново з елегантною розкішшю. При цьому не були забуті пристосування для природничонаукових занять: фізичний кабінет і невелика лабораторія. В одній з галерей замку була також влаштована маленька сцена для вистав. У кожного була своя половина. У нього бібліотека, кабінет і лабораторія; у неї - теж. Ця пані препарувала жаб, робила хімічні досліди, вивчала фізику і математику. Вона перевела на французьку мову книгу «Математичні принципи» Ньютона».

Вольтер пише: «Народжена для істини, вона, зміцнивши свої пізнання, додала до цієї книги, зрозумілої дуже небагатьом, алгебраїчний коментар». І додає, що коментар редагував один з кращих математиків тих днів Клеро, так що «нашому віку мало честі, що коментар залишився непоміченим».

з 1734 по 1739 Вольтер прожив майже безвиїзно в Сірее. Потроху в пустельний замок стали наїжджати гості. Відомі вчені Мопертюї, Клер, Бернуллі гостювали по черзі в Сірее. Німецький учений, послідовник Лейбніца Кеніг прожив там навіть цілих два роки, допомагаючи господині в її вчених працях. Італієць Альгаротті привозив на її суд свою популяризацію філософії Ньютона, призначену «для дам». Заїжджали в Сірей і знайомі дами, але набагато рідше, - дамам Емілія взагалі не подобалася.

Маркіз дю Шатле іноді зупинявся в Сірее, і між ним та Вольтером, по видимому, існували почуття поваги і дружба.

Головним предметом занять Вольтера і його божественної Емілії (так називав він її у віршах і листах) були точні науки, до яких мала пристрасть маркіза, що не любила ні віршів, ні історії - улюблених предметів Вольтера. У Емілі інтерес до математики та природничих наук збігається з її сердечними справами.

Вона вивчає математику під керівництвом найвидатніших математиків того часу: Мопертюї, Бернуллі, Кеніга, де Клеро та ін. Один з найзначніших викладачів був П'єр Луї де Мопертюї, відомий математик і астроном того періоду, якого маркиза часто ставила в глухий кут своїми питаннями. Її цікавість і упертість, її жорсткі питання, на які часто неможливо було відповісти, змушували його порушувати звичний спосіб життя і займатися з нею понаднормово.

У результаті такої поведінки у неї часто виникали суперечки зі своїми наставниками. Наприклад, Самуель Кеніг після того, як вона опублікувала свою книгу в 1740 році, пустив слух, що вона просто виклала його ідеї. У Емілі це викликало обурення і вона звернулася за допомогою до Академії наук і до Мопертюї, з яким вона обговорювала цю книгу задовго до роботи з Кенигом.

Навесні 1748, Емілі закохалася в маркіза Жана Франсуа де Сент-Екзюпері Ламберта, молодого красеня офіцера і маловідомого поета. Він не поділяв її пристрасть до життя і роботи, але їхні стосунки розвивалися. Це, однак, не похитнуло її дружби з Вольтера. Дізнавшись про зраду «Божественної Емілії» Вольтер розлютився, але не надовго. «Мій друг, - сказала вона йому, - ви ж самі говорили, що не можете мене любити так, як було спочатку, без шкоди для свого здоров'я. Невже ви будете сердитися, якщо один з ваших друзів зважився допомогти вам?». Вольтер, убитий логікою подруги, змирився.

Навіть коли він дізнався,  що вона чекає дитину  від Ламберта,  Вольтер був поруч, щоб підтримувати її. 
Під час вагітності в 1749 її найголовнішою турботою було побоювання, що її «Коментарі» до зробленого нею перекладу «Принципів" Ньютона залишаться не закінченими. Вона була сповнена рішучості завершити переклад і з цією метою вона жорстко регламентує свій спосіб життя. Вона присвячує весь час тільки роботі: піднімається рано вранці і працює до пізнього вечора. Відмовляється від публічного життя і бачиться тільки з кількома друзями. Чим ближче підходив термін, тим напруженіше вона працювала. Вона продовжувала працювати до народження її другої дочки, і, як пишуть дослідники її біографії, дитина абсолютно несподівано народилася в той час, коли маркіза працювала за столом. 2 вересня 1749 вона народила дівчинку. Минуло кілька днів, Емілі почала відновлюватися після пологів і здавалося щасливою.10 вересня 1749 вона несподівано померла від емболії. Вольтер був з нею до кінця. Вийшовши з кімнати свого померлого друга, Вольтер впав без почуттів внизу на сходах, де його знайшов Сен-Ламбер. Її дочка померла незабаром після цього.

Брюс померла у віці сорока трьох років. Багато авторів, що вивчали її коротке життя, вважають, що Емілі була дійсно унікальна жінка і вчений. Вона жила на повну силу як істинно духовно багата людина. Їй вдалося зберегти свою віру і положення у вищому суспільстві Парижа, продовжуючи при цьому зберігати свою любов до математики. Емілі де Шатле була однією з тих жінок, чий внесок сприяв формуванню курсу математики. І хоча вона не створила власного оригінального вчення, її робота з письмового перекладу, коментарі та узагальнення внесли значний внесок у розвиток науки.

Вольтер писав, що

«Вона була великою людиною, чия єдина провина полягала в тому, що вона - жінка».

 

 

 

 

 

 

 

 

СОФІ ЖЕРМЕН

Софі Жермен народилася в Парижі 1 квітня 1776 , за 10 років до Французької революції і через сторіччя після Наукової революції. Закони Ньютона управляли Всесвіту , в той час як укази Людовика XVI правили Францією. Жермен підтримувала політичні зміни , слугувала прогресу математики і фізики і рішуче боролася з бар'єрами , що перепиняють жінкам шлях до наукової діяльності.

Її батько , Амбруаз -Франсуа Жермен був цілком поглинений Французькою революцією . Він належав до прошарку ліберальної утвореної буржуазії. Рід Жермен з покоління в покоління займався торгівлею , і сім'я мала достатню стан . Захищаючи інтереси своєї спільноти , Амбруаз був депутатом Асамблеї , куди він був обраний в 1789 році.

У віці 13 років Софі , за свідченням знайомих , була боязким , незграбним підлітком. Вважаючи , що її родина схиблена на грошах і політиці , вона знаходила притулок у батьківській бібліотеці. Там і почалося її інтелектуальний розвиток. Софі вивчила математику , прочитавши всі книги , які їй вдалося знайти. Так само як вона не могла зрозуміти інтересу своїх батьків до політики , вони не розуміли її захоплення математикою , вважаючи її інтереси дивовижними для її віку і несумісними з її статтю .

Італійський математик Дж. Т. Лібрі - Каруччі розповідав , як Софі долала наполегливе бажання батьків , щоб вона кинула захоплення математикою . Коли всі в будинку лягали спати , вона займалася при свічках. Зимовими ночами , коли чорнило замерзали в чорнильниці , вона читала , загорнувшись у ковдри . її рішучість виявилася сильнішою батьківської волі . і незважаючи на її « дивні» інтереси , батько надавав їй матеріальну підтримку протягом усього життя. Софі не вийшла заміж і не добилася професійного становища , яке дало б їй засоби до існуванню .

Софі Жермен дуже любила читати про Архімеда в « Історії математики» Жана Етьєна Монтукла . Подумки вона ототожнювала себе з Архімедом , які боролися за продовження своїх досліджень під час нападу римлян на Сіракузи. Вона удосконалювала свої знання , просуваючись від трактату Етьєна Безу про математику до робіт Ньютона і швейцарського математика Леонарда Ейлера .Родичі , друзі і наставники мало уваги звертали на інтереси і здібності юної Софі . Вони не бачили сенсу в тому , щоб серйозно займатися розвитком інтелектуальних здібностей молодої

Софі Жермен стала автором видатних математичних робіт , але як жінка , що належала середньому класу і жила в часи Французької революції , вона так і не отримала заслуженого визнання в науковому світі . Тепер у дворі школи ім. Софі Жермен у Парижі їй встановлено пам'ятник.

Жермен було 19 років , коли була заснована Політехнічна школа. Вона діставала конспекти лекцій з багатьох курсам , включаючи аналіз , який читав Жозеф Луї Лагранж , і хімію , яку читав Антуан Франсуа Фуркруа . На одному із занять Лагранж попросив студентів викласти письмово свою думку про прочитане їм курсі . Побоюючись , що її твір не стануть читати , Жермен представила свою роботу під ім'ям колишнього студента Антуана Огюста Леблана . ( До речі, не відомо , чи давав на це свою згоду Леблан . )

Наукова освіта Жермен було найвищою мірою незвичайним для жінки її класу. У XVIII столітті наука викладалася деяким жінкам з аристократичних кіл у популяризувати викладі , за підручниками, написаними спеціально для цієї мети. Про науку в них говорилося рівно стільки , скільки було достатньо , щоб жінка могла підтримати « вчений розмова» в аристократичних салонах. Одну з найбільш примітних книг в цьому жанрі «Філософія сера Ісаака Ньютона у викладі для дам » написав Франческо Альгаротті .

Альгаротті вважав , що жінок цікавить лише лицарська романтика і любов , і тому він викладав фізику з урахуванням цієї обставини. Його книга побудована на діалозі між якоїсь маркізою і її співрозмовником . В одній зі сцен співрозмовник пояснює закон про зворотну квадратичної залежності. Він каже , що . сила взаємного тяжіння або інтенсивність світла , наприклад , зменшується пропорційно квадрату відстані між об'єктом і спостерігачем Маркіза відповідає, що їй знайоме це поняття : «У мене мимоволі виникає асоціація ... мені здається , що ця зворотній квадратична залежність ... спостерігається навіть в любові. Скажімо , після восьми днів розлуки любов стає в шістдесят чотири рази слабкіше , ніж у перший день ». Книга сповнена прикладами подібного роду , серед яких наведені в ній небагато суворі фізичні пояснення буквально губляться .

Жермен терпіти не могла такий фривольної літератури . Жозеф - Жером Лаланд одного разу привів її в лють , натякнувши , що вона не зможе зрозуміти роботу П'єра Симона Лапласа , якщо попередньо не прочитає книгу Лаланда «Астрономія для жінок». Жермен публічно оголосила , що ніколи паче не розмовлятиме з Лаландом .

Її утворення було безсистемним і непослідовним . Вона була удостоєна зустрічі з Лагранжем і декількома іншими вченими. Деякі з них запропонували її увазі невеликі завдання . Однак Жермен прагнула до того , щоб отримати професійну підготовку , але така можливість їй так і не представилася .

Жермен була ізольована не тільки від суспільства вчених мужів , а й від інших освічених жінок . Її соціальне положення не дозволяло їй спілкуватися з жінками з аристократичних кіл. Крім того , у неї не було родичів або близьких знайомих серед освічених чоловіків , які могли б представляти її ідеї в науковому світі ; саме такі зв'язки сприяли , зокрема , графині Готта і мадам Лаланд .

Можливо , Жермен і сама в якійсь мірі сприяла своєї ізоляції . За своєю природною скромності і сором'язливості вона уникала світського життя. Подібно великим енциклопедистам , твори яких її займали , вона вважала, що її наукові роботи самі по собі принесуть їй неминуще визнання наперекір забобонам суспільства.

Жермен опинилася осторонь від наукового співтовариства в той період , коли воно привертало до себе все більше число людей , організовувало все більше наукових установ і як ніколи раніше сприяло співпраці між вченими. Вона вже не займалася в холодній спальні , але з радістю подолала б крижану стіну , щоб її робота отримала якесь визнання .

На межі XVIII і XIX століть Жермен надалася хороша можливість проявити свої здібності в області теорії чисел. Перші професіонали , з якими вона познайомилася , Лагранж і Адрієн Марі Лежандр , обидва дуже цікавилися цим предметом і заохочували її заняття .

Через кілька років вона вже добре розумілася на складних методах , викладених у « Арифметичних дослідженнях » німецького математика Карла Фрідріха Гаусса. Перебуваючи під сильним враженням від книги , Жермен послала її автору близько десятка листів в період між 1804 і 1809 роками. Свої листи вона підписувала псевдонімом « Леблан » , оскільки боялася « насмішок з приводу жінки- вченого» .

Друзі і суперники Софі Жермен були в числі найбільш знаменитих математиків і фізиків XIX століття , але більшість вчених ставилися до неї з байдужістю . На початку своєї наукової кар'єри Жермен листувалася з Карлом Фрідріхом Гауссом з питань теорії чисел. Жозеф Луї Лагранж заохочував її у вивченні математики і фізики. Приблизно в 1814 році вона змагалася з Симеоном Дені Пуассоном , намагаючись побудувати теорію пружності . наприкінці свого життя вона співпрацювала і дружила з Жаном Батистом Жозефом Фур'є .

У своєму першому листі Гауссу Жермен обговорює рівняння Ферма

xⁿ + yⁿ = zⁿ,

де  x, y, z и n- .. цілі числа П'єр Ферма вважав, що міг довести , що рівняння не має рішення для п великих 2 Це припущення , відоме як остання теорема Ферма , було доведено в 1995 році.

Жермен відкрила , що рівняння Ферма не має рішення , коли п одно n- 1 , де р - . Просте число виду 8k +7 (Наприклад, k рівне 2, то p — просте число, а саме 23, и n рівне 22. ) Жермен пояснила своє доказ Гауссу і зауважила: «На жаль , глибина мого інтелекту поступається моєї ненаситності , і я відчуваю збентеження через те , що турбую геніальної людини , не маючи по суті нічого вартого , щоб запропонувати його увазі , окрім захоплення , яке поділяється усіма його читачами ».

Гаусс відповів: « . Я в захваті від того , що арифметика знайшла у вашій особі такого здатного одного Ваше нове доказ ... вельми витончено , хоча охоплює , мабуть , досить окремий випадок і не може бути застосоване до інших числах ».

У 1806 році Жермен послала лист Гауссу з Жозефом - Марі Пернеті , армійським офіцером , який був її приятелем. Жермен турбувалася про безпеку Гаусса , оскільки незадовго до цього Наполеон опанував більшою частиною Пруссії. Вона сказала Пернеті , що боїться , як би Гаусса не осягнула та ж доля , що і Архімеда , який був убитий римлянами. Пернеті велів передати з посильним , що Гаусс живий, здоровий , але що математик не знає , хто така Софі Жермен. У своєму наступному листі Гауссу Жермен ( вона ж Леблан ) відкриває своє справжнє ім'я.

Гаусс був вельми здивований і втішений . «Жінка через свою стать і наших забобонів зустрічається зі значно більш важкими перешкодами , ніж чоловік , осягаючи складні наукові проблеми. Але коли вона долає ці бар'єри і проникає в таємниці всесвіту , вона безсумнівно проявляє благородну сміливість , винятковий талант і вищу геніальність ». у своїх похвалах на адресу Жермен Гаусс був щирий . Це, зокрема , підтверджується в його листах німецькому астроному Генріху Ольберс .

У 1808 році Жермен пише новий лист Гауссу , говорячи в ньому про те , щo стане найбільш блискучою її роботою в теорії чисел Жермен довела , що якщо х, у і z - цілі числа і якщо

x⁵ + y⁵ = z⁵,

то або х , або у, або z повинні ділитися на 5. Теорема Жермен з'явилася важливим кроком на шляху до доказу останньої теореми Ферма для випадку , коли n=5.

Гаусс так ніколи і не висловив своєї думки з приводу теореми Жермен. Якраз перед цим він став професором астрономії в Геттінгенському університеті і змушений був відкласти свої дослідження в теорії чисел. Він був цілком поглинений професійними й особистими проблемами.

В основному теорема Жермен залишалася невідомою У 1823 році Лежандр згадує її у своїй роботі , де описує свій доказ останньої теореми Ферма для випадку , коли n=5.( У 1676 році Бернар Френікля де Бессі довів теорему для n = 4 ; . 1738 року Ейлер знайшов рішення для n = 3 . ) Теорема Жермен була першим важливим результатом , касавшимся останньої теореми Ферма , з 1738 року аж до досліджень , проведених Ернстом Е. Куммером в 1840 році.

У своїх дослідженнях з теорії чисел Софі Жермен покладалася на направляє вплив Гаусса. Коли їх листування припинилося , вона стала шукати нові завдання і нових наставників. У 1809 році вона зацікавилася темою , яка згодом лягла в основу її найкращих робіт . Вона намагалася пояснити класичні експерименти Ернста Ф. Хладни , німецького фізика , що досліджував коливання пружних пластин.

У своїх експериментах Хладни насипав дрібний пісок на скляну пластинку. Потім він проводив смичком по ребру пластинки , викликаючи коливання . Пісок відскакував від вібруючих областей і збирався в « вузлах » , точках , що залишалися нерухомими. Через кілька секунд пластинка покривалася поруч піщаних кривих. Конфігурація рисунка була симетричною і вельми ефектною - . вона складалася з зірок і інших геометричних фігур ( див. малюнок нижче) Загальний малюнок залежав від форми пластини , положення опор і частоти вібрації.

 

Фігури Хладни утворюються , коли поверхня , покрита піском , починає вібрувати. Піщинки збираються уздовж ліній з найменшою амплітудою вібрацій. Софі Жермен внесла важливий внесок у математичну теорію, що пояснює ці фігури. Ілюстрація відтворена з видання 1809 роботи Ернста Ф. Хладни .

Під час свого візиту до Парижа в 1808 році Хладни продемонстрував свої досліди перед аудиторією з 60 математиків і фізиків Першого класу Французького інституту , відділення Французької академії наук . Досліди Хладни привели вчених у таке здивування , що вони попросили його повторити свої досліди перед Наполеоном. Побачене справило на імператора враження , і він погодився , що вченим Першого класу слід заснувати спеціальну медаль вагою в один кілограм золота і присудити її тому , хто зуміє дати теоретичне пояснення дослідів Хладни . у 1809 році був оголошений конкурс і встановлений термін його закінчення для підбиття підсумків. термін закінчувався через два роки.

Жермен вхопилася за цю можливість. Протягом більше десяти років вона буде намагатися побудувати теорію пружності , конкуруючи або співпрацюючи з найвидатнішими математиками і фізиками . Вона буде відчувати гордість від усвідомлення того , що внесла свій внесок у дослідження , що знаходилися на передньому краї науки XIX століття .

Проте Жермен залишиться осторонь від наукового співтовариства. Етикет вимагав , щоб вона одержувала листа з офіційним запрошенням всякий раз , коли хотіла відвідати наукову установу. Запрошує повинен був забезпечити їй транспорт і супровід . Ці формальності заважали їй вільно обговорювати з іншими вченими цікавили її питання . Як наслідок цих обмежень , їй довелося подолати чимало труднощів , щоб переключитися з теорії чисел на теорію пружності .

Щоб увійти в курс теорії вібрацій , вона звернулася до таких книг , як «Аналітична механіка» Лагранжа і робіт Ейлера про коливання пружних стрижнів. Жермен намагалася пояснити поведінку пружних пластин , застосовуючи методи , якими користувався Ейлер . Він припускав , що прикладається до стрижня сила викликає внутрішнє пружне протидія , і стверджував , що сила пружності в будь-якій точці стержня пропорційна його кривизні . Під впливом робіт Ейлера Жермен прагнула до того , щоб побудувати аналогічну гіпотезу. Вона припустила , що в будь-якій точці поверхні сила пружності пропорційна сумі величин кривизни двох головних кривих в цій точці. Головні величини кривизни являють собою максимальне і мінімальне значення кривизни всіх кривих при перетині поверхні перпендикулярними до неї площинами .

Поняття кривизни лежало в основі роботи Софі Жермен з теорії пружності . В будь-якій точці криву можна апроксимувати окружністю з тією ж дотичній , що і у кривої в даній точці . Кривизна обернено пропорційна радіусу кола . Для поверхні кривизна в точці визначається кривизною кривих , утворених перетинами поверхні з площинами , перпендикулярними поверхні в цій точці. з усіх таких кривих вибирається найбільша і найменша кривизна , які називаються головними величинами кривизни.

У 1811 році Жермен виявилася єдиним учасником конкурсу , але її робота не була удостоєна премії. Вона не зуміла вивести свою гіпотезу з фізичних принципів , та й не могла зробити цього в той час , оскільки їй не вистачало знань у математичному аналізі та варіаційному численні .

Проте її робота сприяла подальшому прогресу в цій області Лагранж , що був одним з членів журі конкурсу , виправив деякі помилки в обчисленнях Жермен і вивів рівняння , яке , як він вважав , могло описувати фігури Хладни Згідно міркуванням Лагранжа , якщо г - це амплітуда вібрацій і якщо г мало , то справедливо рівняння :
 

∂2z ∂t2

+ k2

(

∂4z ∂x4

+

∂4z ∂y4

+

∂4z ∂x2∂y2

)

= 0,

 

де  t - час, k - константа , а х і в представляють координати точок на поверхні пластини.
У 1811 році конкурс був продовжений ще на два роки , і знову Жермен була єдиним його учасником. Вона продемонструвала , як рівняння Лагранжа породжує фігури Хладни в декількох простих випадках. Однак вона не змогла вивести рівняння Лагранжа з фізичних законів. За свою роботу вона була удостоєна похвальною грамоти вчених Першого класу.

Приблизно в цей же час на інтелектуальну територію Жермен почав вторгатися Симеон Дені Пуассон . Надалі йому судилося стати її головним суперником. На відміну від Жермен Пуассон підійшов до теорії пружності , розташовуючи всіма засобами , доступними вченому XIX століття.

Пуассон вступив у Вищу політехнічну школу в 1789 році у віці 17 років. Лагранж і Лаплас помітили його здібності у вирішенні математичних завдань і хороше абстрактне мислення. За підтримки Лапласа Пуассон швидко просувався з академічного сходах. Він став професором в Політехнічній школі і на факультеті природничих наук в Парижі. Він часто відвідував засідання знаменитого наукового товариства Société d'Arcueil , куди приходили деякі найвидатніші вчені , щоб обговорити цікаві роботи або продемонструвати нові експерименти. Керували діяльністю товариства Лаплас і Клод Луї Бертолле , а Пуассон був консультантом в галузі математики. в 1812 році Пуассон , що вже встиг проникнути в саме серце наукової спільноти , був обраний до Перший клас .

Пуассон прагнув пояснити коливання пружних пластин на основі фізичних законів Ньютона і його фізичної моделі . Почавши з припущення , що пластина складається з молекул , які взаємно притягують і відштовхують один одного , Пуассон потім зробив ряд інших , здавалося , цілком розумних припущень. Міркуючи таким чином , він вивів надзвичайно складну формулу і , спростивши її , прийшов до рівняння Лагранжа . За сучасними уявленнями допущення Пуассона здаються абсурдними , і його спроба вивести рівняння Лагранжа була успішною лише тому , що він знав про роботу Жермен і Лагранжа .

У 1814 році Пуассон опублікував статтю про пружних пластинах. Як член Першого класу , він не брав участь у конкурсі. Але його колеги вважали , що Пуассон знайшов фізичне пояснення для фігур Хладни . Приз же залишився нікому не присвоєним .

«Я дуже шкодувала про те , що не знала змісту роботи Пуассона , - писала Жермен в 1815 році в своєму есе , присвяченому теорії пружності - . Я витрачала дорогоцінний час , очікуючи публікації » В цьому есе вона піддала критиці підхід Пуассона , намагаючись запропонувати своє власне пояснення . Жермен постулировала , що пружна сила пропорційна доданої ззовні силі і пропорційна деформації поверхні. сила в кожній заданій точці пропорційна сумі всіх значень кривизни для кривих , що проходять через цю точку . Потім вона показала , що сума всіх вигинів зводиться до суми максимальної і мінімальної кривизни. І нарешті , вона вивела рівняння Лагранжа з останньої суми.

Це есе стало третьою спробою Жермен виграти конкурс , членами журі якого цього разу були Лежандр , Лаплас і Пуассон Вони не могли прийняти її постулату про те , що результат впливу - деформація - . Обов'язково пропорційний самому впливу , тобто доданої силі На насправді пройдуть десятиліття , перш ніж цього буде знайдено пояснення . При цьому застереженні , журі присудило Жермен премію Першого класу. Жермен не з'явилася на церемонію вручення нагороди. Можливо вона вважала , що судді не оцінили гідно її роботу , або ж вона просто не хотіла з'являтися на публіці.

Для Жермен присудження премії стало формальним визнанням її наукової компетентності . Це додало їй впевненості і підвищило авторитет. Однак вчені не висловили їй належної поваги . Пуассон послав їй небагатослівне формальне привітання . Він уникав серйозних дискусій з нею і ігнорував її при зустрічах в суспільстві. Кілька років тому вона розглядала себе як слабенького новачка в компанії гігантів. Тепер вона вже не відчувала захоплення від своїх колег.

Незабаром вона піднялася духом , подружившись з Жаном Батистом Жозефом Фур'є . Жермен і Фур'є , обидва постраждали через суперництво з Пуассоном , і обидва однаково не любили його . Завдяки Фур'є , Жермен почала брати участь у діяльності паризького наукового співтовариства. Вона відвідувала засідання Академії наук і була першою жінкою , яка приходила на ці засідання в особистій якості , а не як дружина когось із її членів.

У 20 -х роках XIX століття у неї виникли честолюбні плани в галузі теорії чисел , де вона сподівалася удосконалити свої докази і продовжити раніше розпочаті роботи . Жермен і Лежандр працювали в цій галузі як рівноправні партнери. Вона також опублікувала огляд своїх робіт з теорії пружності . У цей час Жермен цікавилася різними областями наукового знання і спілкувалася з інтелектуальною елітою. Всім імпонували її невгамовне цікавість і властиве їй чарівність .

Хоча Жермен виразно заслужила своїми роботами наукового ступеня , вона так ніколи її і не отримала. У 1830 році Гаус не зумів переконати професуру Геттінгенського університету присвоїти їй звання почесного доктора наук .

Захворівши на рак грудей , Софі Жермен після дворічної боротьби з хворобою померла 27 червня 1831 у віці 55 років У свідоцтві про смерть проти її прізвища значилося rentere : . «Персона , располагавшая приватними засобами» , що на практиці означало «незалежна жінка».

Перед смертю вона накидала начорно філософське есе , яке не встигла закінчити. Воно було опубліковано посмертно під заголовком «Загальні міркування про науках і літературі». У своєму есе вона намагалася виділити інтелектуальний процес у всіх видах людської діяльності і вважала, що інтелектуальна всесвіт наповнена аналогіями . людський дух , згідно з її поданням , розпізнає ці аналогії , що приводить в остаточному підсумку до відкриття природних явищ і законів світобудови. нам же в свою чергу слід було б розпізнавати аналогії між життям Софі Жермен і нашої власної , з тим щоб ці аналогії допомогли нам прагнути до досконалості перед обличчям забобонів суспільства.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

СОФІЯ КОВАЛЕВСЬКА

Софія Василівна Ковалевська народилась 15 січня 1850 р. в Москві. Батько її — Василь Васильович Крюковський був військовий. Він брав участь у трьох військових походах, був нагороджений найвищими військовими орденами і медалями.

У 1858 р. в чині генерала артилерії батько вийшов у відставку і переїхав з родиною до свого маєтку в с. Палібіно Вітебської губернії. Тут і пройшли дитячі роки Соні.

Змалку в дівчини проявилися такі риси характеру, як зосередженість, наполегливість у досягненні мети і цілковита самостійність. Читати Соня навчилася сама. Пізніше до дітей взяли вчителів. Гувернантка-англійка вчила Соню хороших манер і англійської мови. Учитель Малевич викладав російську граматику, літературу, математику та інші предмети. Він був широко освіченою людиною, передовим педагогом.

Спочатку арифметики Соня не любила, але згодом захопилась нею: вона розв'язувала задачі за допомогою різних комбінацій чисел, виявляючи в цьому неабияку кмітливість. Малевич дав їй вивчати двотомний курс арифметики французького математика Бурдона, написаний для студентів Паризького університету. Вивчення геометрії також ішло успішно. Інколи, вислухавши доведення вчителя, вона доводила деякі теореми по-своєму.

Коли Соні сповнилось 14 років, під час зимового перебування родини Кркжовських у Петербурзі викладачем математики до неї запросили лейтенанта флоту О. М. Страннолюбського. Вже наперших заняттях викладача здивувало те, що дівчина так швидко засвоювала перші поняття з вищої математики — поняття границі, похідної тощо, "начебто вона їх раніше знала".

Соня пояснила: "У ту хвилину, коли ви пояснювали мені ці поняття, мені раптом пригадалося, що все це було написано в лекціях Остроградського, якими була обклеєна наша кімната, і саме поняття про границю здалося мені давно відомим".

Щоб жити самостійно і вчитися, восени 1868 р. Софія Василівна вступає у фіктивний шлюб (який пізніше став фактичним) з Ковалевським Володимиром Онуфрійовичем.

У житті Софії Василівни починається новий період: вона із захопленням відвідує лекції з фізіології професора Сєченова у Медичній академії, анатомію вивчає в лабораторії професора Грубера, біологію— у Мечникова, хімію — у Зініна і математику — в Страннолюбського. Така багатопредметність у навчанні пояснюється тим, що Софія Василівна готується складати екзамени на атестат зрілості.

Крім цього, вона мріє стати лікарем, щоб бути ближче до народу і краще служити йому. Але склавши екзамени на атестат зрілості, вона віддає перевагу математиці. У тодішній Росії до вищої школи жінок не приймали. Тому подружжя Ковалевських разом із сестрою Софії Ганною виїжджає за кордон. У Гейдельберзі, де в університеті працювали видатні німецькі вчені Кірхгоф, Гельмгольц, Бунзен та ін., вона добилася дозволу відвідувати лекції. Щотижня вона слухала по 22 лекції, з яких 16 — з математики. Навчання в університеті йшло дуже добре.

Наприкінці 1870 р. Софія Василівна закінчує навчання в Гейдельберзі і переїздить до Берліна, щоб продовжувати математичну освіту в столиці Пруссії. У Берлінському університеті працював тоді визначний учений-математик Вейєрштрасс — великий знавець вищих трансцендентних функцій, абелевих і особливо складних еліптичних та ультраеліптичних.

Софію Василівну він прийняв дома і, уважно вислухавши її прохання, запропонував кілька завдань з математики. Завдання виявились досить складними, але Ковалевська з ними впоралась своєчасно. Переконавшись, що завдання розв'язані блискуче, Вейєрштрасс погодився працювати з нею двічі на тиждень по 2 години. Учитись у Вейєрштрас-са було нелегко. Німецький математик Фелікс Клейн говорив, що інтелектуальна сила Вейєрштрасса більше пригнічувала слухачів, ніж сприяла їх самостійній творчості. Софія Василівна, працюючи у Вейєрштрасса, вела власну творчу роботу.

Першу невелику працю вона написала для математичного журналу, але вона не була надрукована через те, що до редакції кількома днями раніше надійшла аналогічна праця іншого автора. У цей період Софія Василівна написала три складних математичних праці. Перша з них називалася "Зведення деякого класу абелевих інтегралів третього рангу до інтегралів еліптичних", її дуже високо оцінив професор Вейєрштрасс.

Друга її праця — "Про форму кільця Сатурна" —доповнювала дослідження Лапласа з цього питання. Третя праця — "До теорії диференціальних рівнянь у частинних похідних" узагальнювала відповідні дослідження самого Вейєрштрасса. До Вейєрштрасса цю тему досліджував відомий французький математик Коші. Теорема, що її довела Ковалевська, належить до класичних, вона увійшла до математичних курсів університету під назвою "теорема Коші-Ковалевської".

У 1874 р. проф. Вейєрштрасс поставив питання перед Геттінгенським університетом про надання С. Ковалевській заочно і без екзаменів ступеня доктора філософії. Він писав, що С. Ковалевська сильна в усіх галузях математики і що кожна з її трьох праць може бути достатньою підставою для присудження їй ступеня доктора наук. Математичний факультет університету розглянув ці праці і дав їм найвищу оцінку. На підставі постанови факультету рада Геттінгенського. університету в липні 1874 р. ухвалила надати С. В. Ковалевській без екзамену і диспуту, заочно ступінь доктора філософії з найвищою відзнакою.

Того ж року Ковалевська повертається до Петербурга. Зайняти посаду викладача математики у вищій школі вона не могла, бо це було жінкам категорично заборонено. Софія Василівна змушена була відійти на деякий час від наукової роботи. Вона поринула у літературно-публіцистичну діяльність: писала для газет наукові нариси і театральні рецензії. У домі Ковалевських можна було зустріти таких визначних учених, як Сєченов, Менделєєв, Чебишов, письменників — Тургенєва, Достоєвського та ін.

Ковалевська показує свої математичні праці Чебишову. Він дав їм високу оцінку за свіжість, глибину думок і, порадив одну з них прочитати на VI з'їзді природодослідників і лікарів, що мав відбутися у Петербурзі в 1879 р. Доповідь Ковалевської на тему "Зведення деякого класу абелевих інтегралів третього рангу до еліптичних інтегралів" вислухали з великою увагою. Видатні вчені М. Є. Жуковський і К. А. Тимирязєв щиро радили їй працювати й далі в цій галузі, бо вона "народилася для математики".

У 1880 р. Ковалевська переїжджає в Москву і просить дозволу складати екзамени на ступінь магістра, але її прохання було відхилено. У 1881 р. вона виїхала у Берлін, а потім у Париж. Але і тут не змогла знайти місця викладача у вищій школі. Того ж 1881 р. Ковалевська повернулася до Росії.

У серпні 1883 р. VII з'їзд природодослідників і лікарів, що відбувся в Одесі, одноголосно обрав Софію Василівну головою математичної секції. Тут було зачитано дві доповіді — доктора філософії С. В. Ковалевської і професора Московського університету М. Є. Жуковського. Доповідь С. В. Ковалевської "Про інтегрування диференціальних рівнянь з частинними похідними, що визначають заломлення світла в прозорому кристалічному середовищі" викликала великий інтерес.

Наступного, 1884 р. Софія Василівна зробила доповідь на цю саму тему на засіданні Паризької академії наук. Пізніше її було надруковано в записках Паризької академії наук і Стокгольмської академії наук. Праця була високо оцінена вченими всього світу, вона принесла авторці широку популярність у наукових колах.

На VII з'їзді природодослідників Софія Василівна зустрілась з професором Стокгольмського університету Міттаг-Леффлером і дістала запрошення зайняти посаду приват-доцента в новому Стокгольмському університеті. Ковалевська дала згоду і незабаром була запрошена в Стокгольм офіційно.

До Стокгольма Софія Василівна приїхала в листопаді 1883 p., а з січня 1884 р. почала читати лекції про диференціальні рівняння з частинними похідними. У першому семестрі вона читала лекції німецькою мовою, а до початку другого семестру оволоділа шведською мовою настільки, що читала цією мовою лекції шведським студентам.

Рада університету обрала С. В. Ковалевську штатним ординарним професором. Шведські газети помістили її портрети і біографію. Професор Міттаг-Леффлер одержував листи від газетярів Парижа, Лондона і Відня з проханням надіслати портрет і біографію С. В. Ковалевської. Наступного року в Стокгольмському університеті С. В. Ковалевській запропонували читати, крім лекцій з чистої математики, курс лекцій з механіки.

Поряд з читанням лекцій в університеті Софія Василівна наполегливо проводила дослідження. Світову славу Ковалевській принесла її фундаментальна праця "Обертання твердого тіла навколо нерухомої точки". До Ковалевської над цим питанням працювали Ейлер і Лагранж. Після їх праць тільки праці Ковалевської просунули вперед розв'язання цієї задачі.

У 1888 р. Паризька академія наук оголосила третій конкурс на кращу працю з цієї теми з видачею премії Бордена на три тисячі франків. Перші два конкурси не дали очікуваних результатів, і премію нікому не присудили. Софія Василівна надіслала свою роботу на конкурс, узявши за девіз французьку приказку: "Говори, що знаєш, роби, що повинен; що буде, те й буде". На конкурс було подано 15 праць.

Спеціальна комісія Паризької академії визнала, що твір під девізом "Говори, що знаєш", відмінний, що в ньому відкрито новий випадок. Враховуючи всі наукові якості цієї праці, комісія ухвалила присудити авторові твору збільшену премію: замість трьох тисяч — п'ять тисяч франків. Ця праця була надрукована в наукових записках Паризької академії наук за 1889 р.

Повернувшись у Стокгольм, Софія Василівна з властивою їй наполегливістю знову взялася за дослідження і написала ще дві праці про рух тіла навколо нерухомої точки, за які Стокгольмська академія наук видала їй премію 1500 крон.

Але слава, блискучі успіхи в науці, вечори і прийоми, що влаштовувались на її честь, не могли заглушити в Ковалевської бажання жити і працювати на рідній землі. Вона робить останню спробу: у квітні 1889 p. виїздить у Росію з надією, що її оберуть членом Петербурзької Академії наук. Зустріли її в Петербурзі сердечно, з радістю. Група визначних учених щиро підтримувала наміри Ковалевської і намагалася допомогти їй. У листопаді 1889 р. за пропозицією академіків Чебишова, Імшенецького і Буняковського її було обрано почесним членом-кореспондентом Петербурзької Академії наук, проте це обрання не давало їй ніяких прав щодо роботи в Росії.

Софія Василівна використала всі можливості, щоб добитись гідної її звання. роботи, але двері до наукових установ перед нею були закриті. Клопотання визначних учених і впливових осіб виявилися марними. Останні надії Софії Василівни залишитися на батьківщині, жити і працювати для рідного народу розвіялися. Вона знову — цього разу назавжди — виїжджає за кордон.

Ковалевська часто говорила, що Швеція стала для неї другою батьківщиною. І це було справді так. У Швеції її шанували, цінували як професора, як громадського діяча, як ученого, її близькими друзями були найкращі представники шведських і норвезьких наукових і літературних кіл: професор Міттаг-Леффлер і його сестра, відома шведська письменниця Анна Шарлота Едгрен, професор Гюльден, який був співробітником Пулковської обсерваторії, відомий норвезький діяч, океанограф і дослідник Арктики Нансен, полярний дослідник член-кореспондент Петербурзької Академії наук Норденшельд та ін.

Особливо близько зійшлася Софія Василівна Ковалевська з письменницею Анною Шарлотою Едгрен. Вони написали велику драму "Боротьба за щастя", яку було поставлено на російській сцені. У цій п'єсі вперше порушувалось питання про роль робітничого класу в розвитку суспільства.

У Стокгольмі С. В. Ковалевська написала також відомий роман "Нігілістка" і повісті "Спогади дитинства", "Сестри Раєвські". Крім цього, Софія Василівна писала статті і замітки на літературні та громадські теми до газет і журналів як російських, так і закордонних.

Повертаючись із подорожі по Італії, Софія Василівна заїхала до Парижа побачитися із своїми знайомими математиками, потім до Берліна, де зустрілася із своїм учителем і другом професором Вейєрштрассом.

На шведському кордоні, чекаючи поїзда, вона довгий час простояла під холодним дощем і застудилась. У Стокгольм вона прибула 23 січня 1891 р. дуже простудженою. Наступного дня вона ще читала лекції в університеті, а ввечері відчула, що дуже хвора. 10 лютого 1891 р. Ковалевська померла від паралічу серця. Чутка про її смерть схвилювала всіх, хто знав про блискучу славу і сумну долю жінки-професора Софії Ковалевської.

У 1896 р. російські жінки на кошти, зібрані комітетом Вищих жіночих курсів та іншими організаціями, поставили на могилі С. В. Ковалевської в Стокгольмі пам'ятник з чорного граніту, вивезеного з Росії.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ЕММІ НЕТЕР

Еммі Амалі Нетер народилася 23 березня 1882 року в німецькому містечку Ерланген (тепер входить до агломераціїНюрнберг землі Баварія) у єврейській родині Макса Нетера. Вона була старшою з 4 дітей.

Спочатку вивчала мови, плануючи стати викладачем англійської та французької^[3]. З цією метою добилася дозволу відвідувати лекції в Ерлангенському університеті, де працював її батько, спочатку вільне відвідування (1900), а з 1904року, коли дозволили жіноче навчання, зарахована офіційно. Проте в університеті лекції з математики захоплювали Еммі більше, ніж будь-які інші. Вона стала ученицею математика Пауля Гордана.

Еммі Неттер здавала перед ним докторський іспит «Про повні системи інваріантів тернарних біквадратних форм» (1907). Вплив Гордана на цю роботу її юності був настільки великим, що в кінці дисертації, яку сама ж згодом назве «джунглями формул», Еммі наведе в символічному записі перелік повної системи інваріантів для заданої тернарної квартики з понад трьохсот форм, а портрет учителя відтоді завжди висітиме над її робочим столом.

Вже в 1915 році Нетер внесла внесок у розробку Загальної теорії відносності. Ейнштейн в листі до світового лідера математиків Давида Гільберта висловив захоплення «проникливим математичним мисленням» Нетер.

Батько Еммі занедужав і вона вела його курс, пізніше вийшов на пенсію. Пізніше померла мати, а брат Фріц, недавній геттінгенський студент-математик, опинився на фронті. У 1916 року Еммі Нетер переїжджає до Геттінгена. Проте отримати для неї місце в університеті було нелегко. На голосуванні переважали докази: «Як почуватимуться, повернувшись, наші вояки, коли їм доведеться вчитися, сидячи біля жіночих ніг?» і «Якщо допустити, щоб жінка стала приват-доцентом, то згодом вона може стати й професором, а то й членом університетського сенату. Та чи дозволено жінці входити до сенату?» не зарадило й рішуче Гільбертове: «Але ж сенат — не лазня!» І все ж він знайшов вихід: Нетер почала читати лекції, що оголошувались під ім'ям професора Гільберта.

У 1919 році, після падіння монархії, Еммі Нетер нарешті стає першою в історії університету жінкою приват-доцентом. Це була найнижча сходинка, навіть не посада. Однак, вже у 1922 року вона Еммі отримала посаду позаштатного екстраординарного професора (тобто асистента). Жартували, що «екстраординарний професор не знає нічого ординарного, а ординарний професор не знає нічого екстраординарного».

У зв'язку з інфляцією і зниженням платоспроможності студентів матеріальний стан Еммі Нетер погіршився. Зусиллями Ріхарда Куранта Нетер почали щомісячно видавати 200–400 марок «викладацької стипендії на прожиття», що потребувало кожного року міністерського затвердження. У Геттінгені вона так і не домоглася штатної посади з гарантованою оплатою. Еммі також не була членом жодної з академій. Її не обрали навіть до геттінгенського королівського наукового товариства.

Традиції, забобони, зовнішні міркування пересилили її наукові заслуги і наукову велич, які на той час вже не заперечувались ніким." (Герман Вейль)

Проте якраз у Геттінгені Нетер заклала основи зовсім нової алгебри, яку тепер називають загальною, або абстрактною (тобто теорію кілець, полів, ідеалів).

Незважаючи на свої математичні таланти, Еммі Нетер, не була блискучим викладачем. «Грації не стояли напевно біля її колиски (Вейль), голос вона мала „гучний і неприємний, а одяг мішкуватий“, викладала ж „кваплячись і збиваючись“. Тож на заняття звичайно приходило від п'яти до десяти слухачів, та й ті за її власними спостереженнями „були чужоземцями“. Усього один раз у визначений час знайшла вона близько сотні студентів і здивувалась: „Ви, певно, помилились аудиторією?“ Коли ж у відповідь зашуміло традиційне човгання ніг, яке замість аплодисментів починає й закінчує університетські години, пройшла вперед і впевнено відпрацювала, отримавши записку: „Гості зрозуміли Вас так же добре, як і будь-хто з Ваших постійних слухачів“.

Еммі Нетер ніколи не вірила в зло, їй навіть у голову не могло прийти, що зло може щось відігравати серед людей» (Вейль).

Її ж власна душевна доброта без найменшого хизування й нещирості, її життєрадісність і доступність, її здатність не помічати несуттєвого, створювали навколо неї атмосферу тепла, спокою і легкої радості. Зворушливою була її любов до учнів, які заміняли їй відсутність власної сім'ї. Жіночість її психіки виявлялась у м'якому й тонкому ліризмі відносин, що зв'язували її з людьми. (Александров)

Ван-дер-Варден як ніхто інший сприяв поширенню її ідей («Сучасна алгебра», Г930-1931). Міжнародний математичний конгрес у Цюриху став справжнім тріумфом для Нетер (Швейцарія, 1932).

У 1932 році Нетер, спільно зі своїм учнем Емілем Артіном, отримує премію Акермана-Тебнера за досягнення в математиці.

У 1933 році з приходом нової влади Еммі Нетер мусить емігрувати. Вона знайшла притулок у жіночому коледжі містечка Брін Мор, що у штаті Пенсільванія (США).

Еммі Нетер померла 14 квітня 1935 року, після невдалої операції з видалення ракової пухлини.

А. Ейнштейн в записці на її смерть відніс Нетер до найбільших творчих геніїв математики.

В основному праці Нетер відносяться до алгебри, де вони сприяли створенню нового напрямку, відомого під назвою абстрактної алгебри. У цю область Нетер внесла вирішальну роль (поряд з Емілем Артіном та її учнем Б. Л. ван дер Варден). Герман Вейль писав:

Значна частина того, що складає зміст другого тому «Сучасної алгебри» (Тепер просто "Алгебри ") ван дер Вардена, має належати Еммі Нетер

Терміни «кільце Нетер», «модуль Нетер», теореми про нормалізацію і теорема Ласкера-Нетер про розкладання ідеалу тепер є основними.

Великий вплив зробила Нетер на алгебрізацію топології, показавши, що так звані «числа Бетті» є всього лише рангами груп гомологій.

Великий внесок зробила Нетер у математичну фізику, де її ім'ям називається фундаментальна теорема теоретичної фізики (опублікована у 1918 році), що зв'язує закони збереження із симетріями системи (наприклад, однорідність часу тягне за собою закон збереження енергії). На цьому підході побудована серія книг «Теоретичної фізики»Ландау-Ліфшиц. Особливо важливе значення має теорема Нетер в квантової теорії поля, де закони збереження, що випливають з існування певної групи симетрії, звичайно є головним джерелом інформації про властивості об'єктів дослідження.

Ідеї ​​і наукові погляди Нетер справили величезний вплив на багатьох вчених-математиків і фізиків. Вона виховала ряд учнів, які стали вченими світового класу і продовжили напрямки, над якими працювала Нетер.

 

 

 

 

 

 

АДА БАЙРОН

(1815 – 1852).

Єдина донька поета Дж. Байрона, також займалася математикою і зокрема математичними машинами. Ада Августа Байрон народилася 10 грудня 1815 року.

 Відтоді цей день вважається Днем програміста на честь народження Ади Августи Лавлейс, єдиної доньки славетного англійського поета Джорджа Гордона Байрона та його дружини Аннабелли Мілбенк

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ОЛЬГА ОЛІЙНИК

Ольга Арсенівна Олійник народилася 2 липня 1925 року в селі Матусів, а шкільні роки провела в містечку Сміла (тепер Черкаської області); з початком війни сім'я економіста евакуювалася разом із заводом до м. Перм (Росія), де Ольга закінчила десятирічку (1942) й вступила на фізмат університету та відвідувала семінар професора Московського університету Софії Яновської, з якою й перебереться до столиці: закінчить з відзнакою мехмат університету ім. Ломоносова (1947) і назавжди зв'яже з ним свою долю — кандидат наук («О топологии, действительных алгебраических кривых на алгебраической поверхности», 1950), доктор («Краевне задачи для уравнений с частными производными с малым параметром при старших производных и задача Коши для нелинейных уравнений в целом», 1954), професор (1955), академік...

Напрямок її наукової діяльності визначився під впливом академіка Івана Петровського — диференціальні рівняння в застосуванні до нестаціонарної фільтрації рідин і газів у пористих середовищах; до роз¬поділу тепла в тілах, які знаходяться в різних фазових станах одночасно — плавлення металу чи танення снігу; до ударних хвиль газової динаміки; до математичної теорії пружності й топології; до руху в'язкої рідини... І праця першої вітчизняної жінки, яка в 29 літ уже стала доктором фізико-математичних наук, знайшла гідне поцінування: найпер¬ша премія Чеботарьова (1952) й перший ступінь премії Ломоносова (1964); іноземний член Італійської АН у Палермо (1967) й почесний член Единбурзького королівського товариства Великобританії (1984); іменна медаль Колеж де Франс і медаль першого ступеня Карлова університету Праги...

 

 

КАТЕРИНА ЮЩЕНКО

Катерина Логвинівна Ющенко (до заміжжя Рвачова) народилася в учительській сім'ї (молодший брат також став академіком). 8 грудня 1919 року в містечку Чигирин (тепер Черкаська область), де «чудодійна кому отруйна, а кому цілюща чигар-«трава» (В. Дарда), й, закінчивши Середньоазійський університет (1942), стала доктором фізико-математичних наук «Деякі питання теорії алгоритмічних мов і автоматизація програмування» (1966), професором Київського університету (1969), членом-кореспондентом АН України (1976), членом міжнародної Академії комп'ютерних наук і систем (1993), заслуженим Соросівським професором (1996), заслуженим діячем науки України (1980). Вона мала 7 винаходів; була співавтором довідників програмістів для машин М-20, «Урал», «Дніпро», «Киев» та посібника «Злементьі программи-рования» ( М., 1961), що витримав п'ять видань іноземними мовами; чотири рази видавалась її монографія «Алгебра. Языки. Программирование» (1974), а труд було поціновано державними преміями України (1978, 1992), премією Ради Міністрів Союзу (1984), премією Глушкова (1985) та орденом княгині Ольги (1999)... 

Катерина Ющенко померла у 2001 році.
 

 

 

 

 

 

ГАЛИНА МАТВІЄВСЬКА

Галина Павлівна Матвієвська народилася 13 липня 1930 року в м. Дніпропетровську, дитинство провела в Харкові, а школу закінчи¬ла (1948) із золотою медаллю в Оренбурзі (Росія), де її батько викладав у педагогічному інституті; у 1954 році закінчила Ленінградський (тепер Санкт-Петербург) університет — кафедра алгебри й теорії чисел, на ступінь кандидата фізико-математичних наук (1958) захистилась, ви¬вчаючи неопубліковані архівні рукописи Леонарда Ейлера з теорії чи¬сел. У 1959 році вона переїжджає до Узбекистану, батьківщину чо¬ловіка, і займається історією східної математики, опанувавши з цією метою арабську мову; захищає в Ташкенті докторську дисертацію «Вчення про число в середні віки» (1968); стає членом-кореспондентом АН, заслуженим діячем науки, лауреатом державної премії ім. Беруні...

 

 

 

 

 

 

 

 

 

ОЛЕНА ДУБИНЧУК

Олена Степанівна Дубинчук народилася 21 травня 1919 року на Вінниччині — у старовинному Ямполі, «місті, що розкинулось у ямі» на Дністрі по сусідству з Молдовою. Ще за два місяці до того її батька, директора школи, забрала страшна епідемія висипного тифу, а через десятиріччя туберкульоз хребта звів у могилу й матір, завідуючу початковою школою. Тож сиротою опікувалась її родина — тітки й, особливо, дядько, Володимир Тарасов — математик, директор школи, заслужений учитель України, що сягнув 90-ліття. У класі Олену постійно призначали бригадиром — такий у ті роки сповідувався метод, а школу вона закінчила відмінницею і 1936 року залишила Поділля та вступила в Києві на мехмат університету, диплом якого довелось одержувати під акомпанемент німецьких бомб у червні 1941. У воєнні та відбудовчі роки вона вчителює в сільських школах поблизу Ростова-на-Дону й Саратова (сьогодні в Росії) та на Київщині. З 1951 року й до останку Олена Дубинчук жила тільки інтересами НДІ педагогіки України: захист дисертації «Вузлові питання арифметики в 5 класі» (1954), проблеми методики математики й профтех-освіти, написання підручників, а ще робота на посаді професора педінституту (тепер Національний педуніверситет ім. Михайла Драгоманова)... її книжки виходили в Києві й Москві, у Болгарії й Польщі та й нинішні старшокласники знаходять в «Алгебрі й початках аналізу» нею підготовлені розділи про степеневу й показникову функції, а також «Вступ до статистики».
	«Як джерельна вода спраглому були її терплячо мудрі коментарі, і лагідна усмішка, і доброта в очах, і теплота розуміння» (Оксана Москаленко, 1999), що «знімало напруження, повертало усі фарби життя» (І. Новик (Білорусь), 1999). «Вона завжди комусь допомагала, хоч сама жила дуже скромно» (Людмила Хлебникова (Київ), 1999), але «мала й домашній ботанічний сад» — неповторну колекцію фіалок, кохаючись в природі, систематично вела фенологічні нотатки, лікувалась фітотерапією... Олени Дубинчук не стало 25 жовтня 1994 року: під час переїзду на роботі її травмувала падаюча книжкова шафа, що згодом призвело до інсульту. Працю ж її відзначено трудовими й освітянськими нагородами, зокрема й медаллю Макаренка.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Висновки

                Життя  жінок – математиків складалося важко. Нелегко було пробивати дорогу до науки жінкам,  долаючи і важкі нострої, і складні умови.  Але, не дивлячись на все, вони своєю працею,  наполегливістю і завзятістю завоювали всесвітнє визнання нарівні з чоловіками – математиками. Вся їх діяльність – це життєвий подвиг.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Додатки