заняття - аукціон з алгебри та початків аналізу на тему: "Методи розв"язування показникових рівнянь" 11 клас
заняття - ауціон проводиться у вигляді розігрування навчальних лотів, які передбачають повторення та узагальнення теоретичного матеріалу та вироблення міцних обчислювальних навичок по розв"язуванню показникових рівнянь.
Заняття - аукціон із алгебри та початків аналізу. 11 клас
Тема: Методи розв’язування показникових рівнянь.
Мета:
- Систематизувати й узагальнити знання, уміння та навички студентів із теми, формувати вміння студентів розв’язувати показникові рівняння різними способами: зведення до однієї основи, до спільного показника, винесення спільного множника за дужки, зведення до квадратного рівняння тощо.
- Стимулювати пізнавальну діяльність, розвивати інтерес до математики; формувати вміння швидко й чітко формулювати власні думки, логічно викладати й відстоювати їх.
- Виховувати працьовитість; прищеплювати бажання мати якісні, глибокі знання; виховувати культуру математичних записів.
- Розвивати творчі здібності, увагу та пам'ять.
Тип заняття: узагальнення, систематизація та застосування знань, умінь,
навичок.
Хід заняття
І. Організаційний етап.
Афоризм «Якщо запастися терпінням
і виявити старання,
то посіяні насіння знання
неодмінно дадуть добрі сходи».
Леонардо да Вінчі
ІІ. Проведення аукціону.
Лот 1. «Пошуковий» (стартова ціна 2 бали)
Студенти відповідають на запитання «Як формувалось і входило в математику поняття показникових рівнянь?»
Лот 2. «Теоретичний» (стартова ціна 1 бал)
- Які рівняння називають показниковими?
-
Скільки розв’язків має рівняння
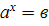 (
(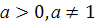 )?
)?
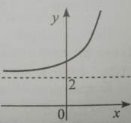
- Через яку точку проходить графік кожної показникової функції?
- Чи може значення показникової функції бути від’ємним або
дорівнювати нулю?
- При якій умові показникова функція зростає? А при якій – спадає?
- Які формули та показникові співвідношення вам відомі?
Лот 3. «Усний» (стартова ціна 1 бал).
- Розв’яжіть рівняння
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д)![]() ;
;
- При яких значеннях х виконується рівність:
а)![]() ; б)
; б) ![]() ; в)
; в)![]() ; г)
; г) ![]() ;
;
- Знайдіть значення х, для яких
а) ![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г) ![]() ;
;
- Обчисліть
а) ![]() ; б)
; б) ![]() ; в)
; в)![]() ; г)
; г) ![]() ; д)
; д) ![]() ;
;
Лот 4. «Практичний» (стартова ціна 2 бали)
-
Метод приведення рівняння до спільної основи, тобто до рівняння
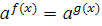
Як відомо, показникова функція ![]() , де а > 0,
, де а > 0, ![]() монотонна, тому кожне своє значення вона приймає тільки при одному значенні аргумента. Із рівності
монотонна, тому кожне своє значення вона приймає тільки при одному значенні аргумента. Із рівності ![]() випливає, що
випливає, що ![]() .
.
№1 Розв’яжіть рівняння ![]() .
.
Розв’язання.
![]() ;
; ![]() ;
; ![]() ; х=2
; х=2
Відповідь: 2.
№2. Розв’яжіть рівняння ![]() .
.
-
Записавши рівняння у вигляді
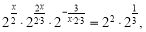 прирівняємо показники при основі 2:
прирівняємо показники при основі 2: 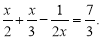
Далі маємо: ![]() .
.
- Метод винесення спільного множника за дужки.
№1 Розв’яжіть рівняння ![]() ;
;
Розв’язання.
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
; ![]() ;
; ![]()
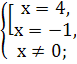
Відповідь: -1;4.
- Метод введення нової змінної.
№1 Розв’яжіть рівняння ![]()
Розв’язання
![]() ;
; ![]() ;
; ![]() ;
;
Нехай ![]() , тоді
, тоді ![]() ;
;
![]() ;
; ![]() ;
;
Отже, 1) ![]() ; х=1; 2)
; х=1; 2)![]() ; х=0.
; х=0.
Відповідь: 0; 1.
№2 Розв’яжіть рівняння ![]()
-
Позначивши
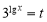 , дістанемо:
, дістанемо:
![]() ;
;
![]() .
.
№3 Розв’яжіть рівняння ![]()
-
Позначивши
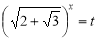 , дістанемо
, дістанемо 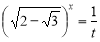 ;
; 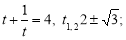
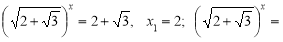
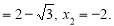
№4 Розв’яжіть рівняння ![]() .
.
-
Позначивши
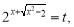 дістанемо:
дістанемо: 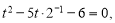
 ;
; 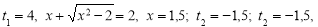
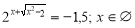 .
.
4 .Метод зведення до однорідних рівнянь.
№1 Розв’яжіть рівняння ![]() .
.
Розв’язання.
Зведемо всі степені до двох основ 4 і 9:
![]() .
.
Маємо однорідне рівняння (у всіх членів однаковий сумарний степінь – 2х). Для його розв’язування поділимо обидві частини на ![]() .
.
![]() .
.
Заміна ![]() дає рівняння
дає рівняння ![]() ;
; ![]() ;
; ![]() ;
;
Обернена заміна: ![]() ;
; ![]() ; х=0.
; х=0.
![]() ;
; ![]() ; 2х=1;
; 2х=1; ![]() .
.
Відповідь: 0; ![]() .
.
№2. Розв’яжіть рівняння ![]() .
.
-
Перепишемо рівняння у вигляді:
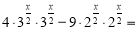
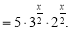 Виконавши заміну
Виконавши заміну 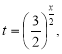 дістанемо
дістанемо 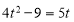 , звідки
, звідки 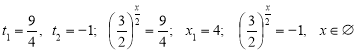 .
.
№3 Розв’яжіть рівняння ![]()
- Запишемо рівняння у вигляді:
![]()
Позначивши ![]() , дістанемо:
, дістанемо:
![]() .
.
- Функціонально - графічний метод.
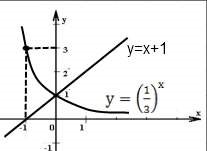
№1 Розв’яжіть графічно рівняння ![]()
Розв’язання.
Побудуємо графіки функцій ![]() ,
, ![]() в одній системі координат. Графіки
в одній системі координат. Графіки ![]() і
і ![]() перетинаються в точці, абсциса якої х=0.
перетинаються в точці, абсциса якої х=0.
![]()
![]()
Відповідь: 0.
Лот 5. «Перевір себе»
Тест
-
Чому дорівнює
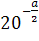 , якщо
, якщо 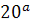 =b
=b
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
-
Запишіть вираз
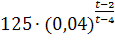 у вигляді степеня з основою 5.
у вигляді степеня з основою 5.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
- Якому з наведених проміжків належать усі розв’язки рівняння
![]() .
.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
-
Розв’яжіть рівняння
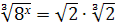 .
.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
-
Якщо
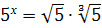 , то х=
, то х=
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
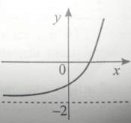
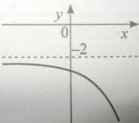
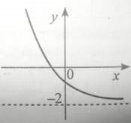
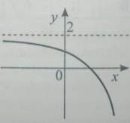
6. Укажіть ескіз графіка функції ![]()
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
|
№ завдання |
1 |
2 |
3 |
4 |
5 |
6 |
|
Відповідь |
В |
Д |
Г |
Г |
А |
Г |
Варіант 1
1. Якщо ![]() , то х = … а) - 3; б) 4; в)
, то х = … а) - 3; б) 4; в) ![]() ; г) - 4.
; г) - 4.
2. Якщо ![]() , то… а)
, то… а)![]() 81; б)
81; б) ![]() 9; в)
9; в) ![]() 27; г)
27; г) ![]() 108
108
3. Якщо ![]() то… а)
то… а)![]() або
або ![]() ; б)
; б) ![]() або
або ![]() ;
;
в) ![]() або
або ![]() ; г) х = 2 або х = 1
; г) х = 2 або х = 1
4. Якщо ![]() , то… а)
, то… а) ![]() 100; б)
100; б) ![]() 2; в) х = 2; г)
2; в) х = 2; г) ![]() .
.
5. Розв’язати рівняння 2х - 2 = 32 - х
а) х = 2; б) розв’язків немає; в) х = - 2; г) х = - 4.
6. Якщо ![]() , то…
, то…
а) ![]() = 4,2; б) 4х = 28; в)
= 4,2; б) 4х = 28; в) ![]() = 4; г)
= 4; г) ![]() = 4;
= 4;
7. Якщо 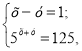
![]() то… а) 2х = 126; б) 2х = 4; в) 2х = 8; г) 2х = 3.
то… а) 2х = 126; б) 2х = 4; в) 2х = 8; г) 2х = 3.
|
№ завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Відповідь |
Г |
В |
А |
Б |
А |
В |
Б |
Лот 6. Підсумковий
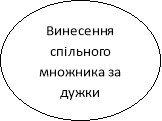
Підсумком бесіди з узагальнення та систематизації набутих студентами знань із теми «Методи розв’язання показникових рівнянь» є складена спільними зусиллями схема.

![]()


![]()



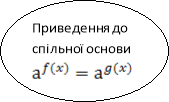

ІІІ. Домашнє завдання
Варіант 2
1. Якщо ![]() , то х = … а) 16; б) 1,5; в) 1
, то х = … а) 16; б) 1,5; в) 1![]() ; г)
; г) ![]() .
.
2. Якщо ![]() , то… а)
, то… а)![]() 5; б)
5; б) ![]() 6; в)
6; в) ![]() 25; г)
25; г) ![]() 5.
5.
3. Якщо ![]() то… а)
то… а)![]() або
або ![]() ; б)
; б) ![]() або
або ![]() ;
;
в) ![]() або
або ![]() ; г) х = 3 або х = 1
; г) х = 3 або х = 1
6. Якщо ![]() , то… а)
, то… а) ![]() 36; б)
36; б) ![]() 2; в)
2; в) ![]() = 2; г)
= 2; г) ![]() .
.
7. Розв’язати рівняння 3х - 4 = 54 - х
а) х = 2; б) х = 0; в) х = 4; г) х = - 4.
8. Якщо ![]() , то…
, то…
а) ![]() = 3; б) 3х = 3; в)
= 3; б) 3х = 3; в) ![]() = 13; г)
= 13; г) ![]() = 3;
= 3;
9. Якщо 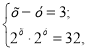
![]() то… а) 2х = 35; б) 2х = 8; в) 2х = 29; г) 2х = - 1
то… а) 2х = 35; б) 2х = 8; в) 2х = 29; г) 2х = - 1


про публікацію авторської розробки
Додати розробку