Обернені тригонометричні функції
- повторити поняття оборотної та оберненої функцій, властивості графіків взаємно-обернених функцій;
- вивчення властивостей обернених тригонометричних функцій .
Урок формування вмінь та навичок
Обернені тригонометричні функції
![]()
Необхідний час – 45 хвилин
Мета уроку: - повторити поняття оборотної та оберненої функцій, властивості графіків взаємно-обернених функцій;
- вивчення властивостей обернених тригонометричних функцій ![]() .
.
Тип уроку: урок формування вмінь та навичок
Структура уроку:
1. Організаційний момент.
2. Повідомлення теми та мети уроку.
3. Актуалізація опорних вмінь та навичок.
- Подання нового матеріалу.
- Підведення підсумків уроку.
Хід уроку
- Організаційний момент.
- Повідомлення теми та мети уроку.
Вчитель наголошує на важливості теми, оскільки на основі цього матеріалу грунтується і вивчення тригонометричних рівнянь.
- Актуалізація опорних вмінь та навичок
У формі фронтальної бесіди проводиться повторення вивченого матеріалу.
Питання для учнів:
Закінчіть математичні твердження:
- Функція, яка набуває кожного свого значення в єдиній точці області визначення називається ... (оборотною);
-
Оберненою до функції
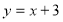 є функція ... (
є функція ... (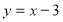 );
);
-
Оберненою до функції
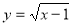 є функція ... (
є функція ... (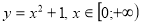 );
);
-
Оберненою до функції
 є функція ... (
є функція ... (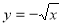 );
);
-
Графіки даної функції і оберненої до неї симетричні ... (відносно прямої
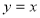 );
);
-
Якщо функція
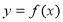 - зростаюча, то обеонена до неї функція ... (зростаюча);
- зростаюча, то обеонена до неї функція ... (зростаюча);
-
Область визначення функції
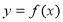 для оберненої функції буде областю ... (значень).
для оберненої функції буде областю ... (значень).
-
Сприйняття і усвідомлення поняття
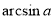 та властивостей функції
та властивостей функції 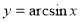 .
.
Наше завдання на уроці – знайти обернену функцію для ![]() . Оскільки одному значенню ординати відповідає безліч значень аргумента, то варто розглянути функцію
. Оскільки одному значенню ординати відповідає безліч значень аргумента, то варто розглянути функцію ![]() на проміжку
на проміжку ![]() , на якому вона зростає, де кожному значенню функції відповідає єдине значення області визначення. Отже, рівняння
, на якому вона зростає, де кожному значенню функції відповідає єдине значення області визначення. Отже, рівняння ![]() на проміжку
на проміжку ![]() має єдиний корінь, який називається арксинусом числа
має єдиний корінь, який називається арксинусом числа ![]() і позначається
і позначається ![]() .
.
Арксинусом числа ![]() називається таке число із проміжку
називається таке число із проміжку ![]() , синус якого дорівнює
, синус якого дорівнює ![]() .
.
Приклади:
Обчислити:
1)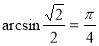 , бо
, бо 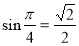 і
і  .
.
2) ![]() , бо
, бо ![]() і
і ![]() .
.
Варто запам’ятати формули: ![]()
Приклади:
Знайти:

Властивості оберненої тигонометричної функції 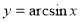 будемо розглядати пригадуючи властивості тригонометричної функції
будемо розглядати пригадуючи властивості тригонометричної функції 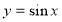 . Результати наших досліджень запишемо в таблицю:
. Результати наших досліджень запишемо в таблицю:
|
№/п |
Функція |
Функція |
|
1. |
|
|
|
2. |
|
|
|
3. |
Функція непарна |
Функція непарна |
|
4. |
Функція зростаюча:
якщо |
Функція зростаюча:
якщо |
|
5. |
Нуль функції: |
Нуль функції: |
|
6. |
|
|
 Виконання вправ:
Виконання вправ:
1) Розташуйте числа в порядку зростання:![]()
а) ![]()
Оскільки функція ![]() зростаюча, то за властивістю зростаючої функції:
зростаюча, то за властивістю зростаючої функції:
![]()
![]()
Відповідь: ![]() .
.
б) ![]() - самостійно 3 хвилини
- самостійно 3 хвилини
Оскільки функція ![]() зростаюча, то за властивістю зростаючої функції:
зростаюча, то за властивістю зростаючої функції:
![]()
![]()
Відповідь: ![]() .
.
2) Знайти область визначення функції:
а) ![]() ;
;
![]() .
.
б) ![]() ;
;
![]() .
.
в) ![]() ;
;
![]() .
.
-
Сприйняття і усвідомлення поняття
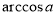 та властивостей функції
та властивостей функції 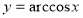 .
.
Функція ![]() спадає на проміжку
спадає на проміжку ![]() , і приймає всі значення від –1 до 1, тому рівняння
, і приймає всі значення від –1 до 1, тому рівняння ![]() на проміжку
на проміжку ![]() має єдиний корінь, який називається арккосинусом числа
має єдиний корінь, який називається арккосинусом числа ![]() і позначається
і позначається ![]() .
.
Арккосинусом числа ![]() називається таке число із проміжку
називається таке число із проміжку ![]() , косинус якого дорівнює
, косинус якого дорівнює ![]() .
.
Варто запам’ятати формули: ![]()
Приклади:
Обчислити:
1)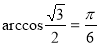 , бо
, бо  і
і 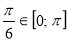 .
.
2) 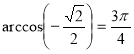 , бо
, бо ![]() і
і ![]() .
.
3)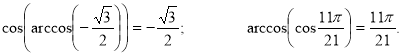
Властивості оберненої тигонометричної функції 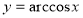 будемо розглядати пригадуючи властивості тригонометричної функції
будемо розглядати пригадуючи властивості тригонометричної функції 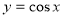 . Результати наших досліджень запишемо в таблицю:
. Результати наших досліджень запишемо в таблицю:
|
№/п |
Функція |
Функція |
|
1. |
|
|
|
2. |
|
|
|
3. |
Функція парна |
Функція ні парна, ні непарна |
|
4. |
Функція спадна:
якщо |
Функція спадна:
якщо |
|
5. |
Нуль функції: |
Нуль функції: |
|
6. |
|
|
Виконання вправ:
1) Які з поданих виразів мають зміст і чому?
а) ![]() ; г)
; г) ![]() ;
;
![]()
![]()
б) ![]() ; д)
; д) ![]() ;
;
![]()
![]()
Відповідь: г), д).
2) Порівняйте числа:
а) 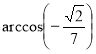 і
і ![]() ;
;
б) ![]() і
і ![]()
Враховуючи, що функція ![]() спадна, то за означенням отримаємо
спадна, то за означенням отримаємо
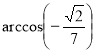 <
< ![]() ;
; ![]() <
< ![]() .
.
3) Побудуйте графік функції ![]() .
.
- Підведення підсумків уроку.
Домашнє завдання: Розділ ІІ §1(2,3).
Запитання і завдання для повторення розділу ІІ №6, 7, 9, 10, 11, 12 (1, 2, 5-8).
1

про публікацію авторської розробки
Додати розробку
