Вчитель Пдіщинської ЗОШ І-ІІІ ступенів

Ніщук Н.І.

Зміст

Зміст

Пам’ятка

Основні задачі на відсотки

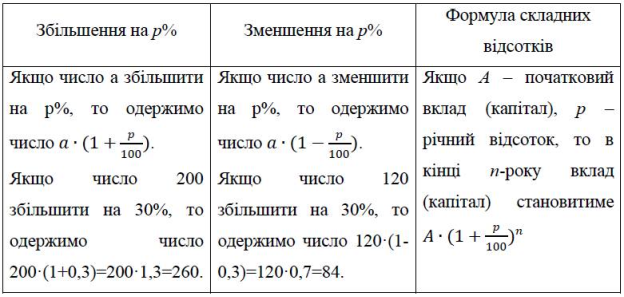
Збільшення (зменшення) числа на декілька відсотків. Формула складних відсотків

Перевірка  початкових знань про відсотки:

Перевірка опорних знань з теми «Відсоткові розрахунки».

Прості відсотки в математиці

Задачі на відсотки — це задачі на пряму пропорційність.

Задачі на суміші

Колективне розв'язування задач

Задачі на відсоткові розрахунки

Задачі для  домашньої роботи

Задачі для  колективної  роботи в навчальних групах

Задачі для самостійної роботи

Самостійна робота

Контрольне  оцінювання з теми  «Відсоткові  розрахунки»

Контрольне  оцінювання з теми  «Відсоткові  розрахунки»

Знаходження відсотків від числа

Знаходження числа за його відсотками

Знаходження відсоткового відношення

Пам’ятка

Основні задачі на відсотки

Для того, щоб знайти р відсотків від даного числа а, треба:

1) перевести р відсотків у десятковий дріб;

2) помножити число а на одержаний десятковий дріб.

    Приклад 1. Знайти 20% від числа 120.

     Розв’язання. 20%=0,2, 120·0,2=24.

     Відповідь: 24.

Для того щоб знайти все число за відомою частиною b і числом відповідних відсотків р, треба:

1) перевести р відсотків у десятковий дріб;

2) розділити b на одержаний десятковий дріб.

    Приклад 2. Знайти число, 12% якого складає 60.

     Розв’язання. 60:0,12=6000:12=500.

     Відповідь: 500.

Щоб знайти відсоток числа b від числа а, треба дріб  помножити на 100%.

    Приклад 3. Скільки відсотків складає число 0,3 від 20?

     Розв’язання. .

     Відповідь: 1,5%.

Збільшення (зменшення) числа на декілька відсотків. Формула складних відсотків

 

Перевірка  початкових знань про відсотки:

1. Десятковий дріб 0,36 відповідає:

 А) 36%; Б)3,6%;  С)0,36%.

2. 10% від 70 дорівнює:

А) 10;   Б) 7;   В)0,7. 

3. Звичайному дробу 3/4 відповідає:

  А) 25%;  Б) 50%;  В) 75%.

4.  Знайдіть  відсоток від числа:  625%  від  ¾; 150 від  1,5;

а) ;  б)   ; в)  ; г) .

Перевірка опорних знань з теми «Відсоткові розрахунки».

ВАРІАНТ 1

1.       Відсотком називається:

а)       сота частина числа;

б)      тисячна частина числа;

в)      десять проміллів.

2.       Щоб знайти р% від числа, треба:

а)       число поділити на р і помножити на 100;

б)      число поділити на 100 і помножити на р.

3.       При р % річних початковий капітал А через n років перетвориться в:

a)  А(1+ 0,01pn)   б) А(1+ 0,01p)n   в)  А(1+ 0,01n)p   г) інша відповідь.     

4. 20% від числа 120 становить:

а) 20; б) 24; в) 600;        г) 480;  д) інша відповідь.     

5. Число, 32% якого становить 16, дорівнює:

а) 200;         б) 512;        в) 50; г) 5,12;  д) інша відповідь.     

6. Відсоткове відношення числа 7 до числа 35 становить:

а) 500%;        б) 7%;      в) 20%;       г) 5%;    д) інша відповідь.     

7. При збільшенні числа на 50% воно збільшується:

а) у 2 рази; б) в 1,5 рази; в) інша відповідь.

8. При зменшенні числа на 25% воно зменшується:

а) в 4 рази; б) в 1,5 рази; в) в 1,25 рази; г) інша відповідь.

9. Число зменшили на 20%. Щоб одержати початкове число, нове треба збільшити:

а) на 20%; б) більше, ніж на 20%; в) менше, ніж на 20%.

10. Відсоткове відношення міді до олова в бронзі становить

400%. Яке відношення олова до міді?

а) 300%;        б) 20%;    в) 25%;       г) 10%.

11. Який відсоток складає мідь в бронзі (див. №10):

а) 75%;       б) 80%;       в) 90%;       г) 40%.

12. Латунь - сплав міді та цинку. Мідь складає 60% сплаву. Яке відсоткове відношення міді до цинку:

а) 60%;       б) 200%;        в) 150%;  г) 200/66 %.   

ВАРІАНТ 2

1.    Проміллем називається:

а)       сота частина числа;

б)      десята частина відсотку;

в)      тисячна частина числа.

2. Щоб знайти число, р% якого дорівнює а, треба:

а) а:100∙р;    б) а:р∙100;   в) інша відповідь.     

3. Нарощений капітал вкладника - це:

а)       сума, яку він поклав до банку;

б)      сума, яку він одержить через певний час;

в)      різниця між одержаною і початковою сумою.

4.       25% від числа 160 становить:

а) 25; б) 64; в) 40; г) 16.

5. Число, 18% якого становить 54, дорівнює:

а) 300;         б) 200;        в) 972;        г) 9,72.

6. Відсоткове відношення числа 13 до числа 52 становить:

а)13%;        б) 52%;       в) 400%;       г) 25%.

7. При збільшенні числа на 25% воно збільшується:

а) у 4 рази; б) в 1,5рази; в) в 5/4 рази; г) інша відповідь.

8. При зменшенні числа на 50% воно зменшується:

а) у 2 рази;   б) в 1,5 рази;   в) інша відповідь.

9. Ціну товару збільшили на  10%.  Щоб одержати попередню ціну, нову треба зменшити:

а) на 10%; б) більше, ніж на 10%; в) менше, ніж на 10%.

10. Відсоткове відношення міді до олова в сплаві становить 300%. Яке відношення олова до міді:

а) 200%;        б) 33-%;      в) 25%     г) 30%;  д) інша відповідь.     

11. Який відсоток складає олово в сплаві (див. №10):

а) 30%;       6)25%;        в) 100/3%;      г) 20% ; д) інша відповідь.     

12. Латунь - сплав міді та цинку. Цинк складає 30% сплаву.

Яке відсоткове відношення цинку до міді:

а) 30%;       б) інша відповідь;      в) 23%;      г) 25%; д) інша відповідь.     

Прості відсотки в математиці

Задача 1. У клас закупили 3 енергозберігаючі вікна, які на 20% дорожчі за прості. Скільки витратили грошей, якщо за звичайні вікна потрібно заплатити 1400 грн.

Розв'язання:

Знайдемо ціну енергозберігаючого вікна

P[в]=1400*(1+20/100)=1680 (грн)

 За три вікна заплатили

1680*3=5040 (грн)

Задача 2. У бочці об'ємом 200 літрів перевозили олію. На станції надібрали 60 літрів. Скільки відсотків від об'яєму залишилося?

Розв'язання:

Завдання полягає у знаходженні кількості у процентах олії від загального об'єму бочки.

200-60=140 (л);

 140/200*100%=70 %

 Залишилося 70% об'єму бочки.

Задача 3. При несвоєчасній сплаті боргів нараховують 2% пені за кожний день просрочення. Яку суму потрібно заплатити через 12 днів після строку погашення 500 грн. боргу?

Розв'язання:

 За формулою простих процентів знаходимо

P[i]=500*(1+2/100*12)=620 (грн)

Потрібно заплатити 620 гривень.

Задача 4. До сплаву масою 600 г, що містить 12 % срібла, додали 60 г срібла. Яким став відсотковий вміст срібла в новому сплаві?

Розв'язання:

 Визначаємо скільки грам срібла в першому сплаві

P[i]=600*12/100=72 (г)

До знайденого значення додаємо 60 грам срібла

P1=72+60=132 (г)

При визначенні відсоткового вмісту срібла не слід забувати, що вага нового сплаву зросла на масу срібла, яку додали.

Якщо б Ви обчислювали наступним чином

132/600*100%=22%

 то отримали б неправильний результат.

ЗАПАМ'ЯТАЙТЕ: в подібних задачах спочатку знаходять міру (вагу, об'єм, довжину) нового об'єкту, а потім знаходять відсотковий вміст.

В заданій задачі новий сплав отримає масу

P2=600+60=660 (г)

а процентний вміст срібла

P1/P2*100%=132/660*100%=20 %

 становитиме 20%.

Задача 5. У саду росли яблуні й вишні, причому яблуні становили 42 % всіх дерев. Вишень було на 48 дерев більше, ніж яблунь. Скільки дерев росло в саду?

Розв'язання:

 До правильної відповіді можна йти декількома способами. Розглянемо наступний із них.

 Нехай яблуні становлять 42% всіх дерев, тоді вишні

100-42=58%.

Вишень на 48 більше ніж яблук.

 Різниця між ними в процентах становить

58-42=16%

 а в кількості – 48 дерев.

Завдання полягає у знаходженні кількості дерев, тому складаємо відношення

16% – 48 дерев

 100 % –Х дерев

Звідси знаходимо кількість дерев у саду

Х=100*48/16=300 (дерев).

Задача 6. За два дні було прокладено кабель. За перший день проклали 56 % кабелю, а за другий — на 132 м менше, ніж за перший. Скільки всього метрів кабелю було прокладено за два дні?

Розв'язання:

 Завдання подібне до попередньої задачі. За другий день проклали

100-56=44%

 кабелю, різниця між першим і другим днем становить

56-44=12%

 і складає 132 метри.

На основі цього складаємо відношення

12% – 132 м

100 % –Х м

Звідси знаходимо довжину

Х=100*132/12=1100 (м)

За два дні проклали 1100 м кабелю.

Задача 7. За перший день хлопчик прочитав 25 % усієї книжки, за другий — 72 % від кількості сторінок, що залишилася, а за третій — решту 84 сторінки. Скільки сторінок у книжці?

Розв'язання:

72 % відсотки від залишку книжки становить

72*(100-25)/100= 54%

На третій день залишалося прочитати

100-25-54=21%

 або 84 сторінки.

Складаємо співвідношення

21% – 84 ст

 100 % –Х ст

 із якого знаходимо

Х=100*84/21=400 (ст),

 що книга містить 400 сторінок.

Складні задачі на прості відсотки

Задача 8. Морська вода містить 5 % солі. Скільки прісної води треба додати до 40 кг морської води, щоб концентрація солі становила 2 %?

Розв'язання:

 Знаходимо вагу солі у 40 кг морської води

40*5/100=2 (кг).

Знаходимо вагу води, яка б містила 2% солі (2 кг)

2% – 2 кг

 100 % –Х кг

 або

Х=100*2/2=100 кг.

Зараз у нас є 40 кг води, тому потрібно додати

100-40=60 кг

 прісної води.

Задача 9. Змішали 30-відсотковий розчин соляної кислоти з 10-відсотковим розчином і отримали 800 г 15-відсоткового розчину. Скільки грамів кожного розчину взяли для цього?

Розв'язання:

 В таких задачах потрібно скласти два рівняння, розв'язування яких і приведе до відшукання потрібних величин.

Позначимо A – вага першого розчину, B – відповідно другого.

Тоді з умови задачі складаємо два рівняння:

 перше стосується процентних співвідношень (*100)

30*A+10*B=800*15

 друге – ваги суміші

A+B=800.

З другого виражаємо одну з невідомих та підставляємо у перше рівняння

A=800-B;

 30*(800-B)+10*B=800*15

 та розв'язуємо його

24000-30*B+10*B=12000;

 20*B=24000-12000=12000;

 B=12000/20=600 (г)

Масу першого розчину знаходимо з залежності

A=800-B=800-600=200 (г).

Отже, потрібно 600 г 30% розчину та 200 г 10 % розчину соляної кислоти.

Задача 10. Родинний бюджет складається з доходів батька та матері за основним місцем роботи в розмірі 2500 щомісячно, доходів від акцій вартістю 50000грн з прибутковістю 15% річних, прибутків від депозитних вкладів у розмірі 70000грн з відсотковою ставкою 7%. Прибутковий податок за основним місцем роботи становить 13%, податок з прибутку з депозитних рахунків – 5%, податок з прибутку з акцій – 30%. Який річний прибуток?

Задачі на відсотки — це задачі на пряму пропорційність.

Задача 1. Зі свіжих слив виходить 21% сушених. Скільки сушених слив можна отримати із 75 кг свіжих?

Розв’язання

Запишемо умову:

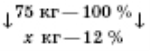
Складемо пропорцію: . Звідси

.

Відповідь: 15,75 кг.

Задача 2. Перший тракторист зорав 40% поля, другий — 35% поля. Яку площу має поле, якщо перший зорав на 4 га більше, ніж другий?

Розв’язання

1) (%) становлять 4 га.

Нехай площа всього поля х га.

.

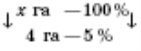
Відповідь: площа поля 80 га.

Задача 3. Із 40 учасників шахового турніру 9 осіб мають звання гросмейстера. Який відсоток учасників турніру становлять гросмейстери?

Розв’язання

•                ,

,

•    .

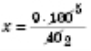Відповідь: гросмейстери становлять 22,5%.

Задачі на суміші

У житті досить часто доводиться змішувати різні рідини, порошки, сплавляти метали. Отже, необхідно робити відповідні розрахунки. При розв'язуванні таких задач зустрічаються терміни концентрація і проба.

Концентрація - це відношення даної складової до загальної кількості суміші чи розчину. На практиці концентрацію виражають у відсотках.

Проба. Вміст дорогоцінного металу в сплаві з іншими металами називають пробою, і позначають числом тисячної частини одиниці. Так, у золоті 583-ої проби на кожні 1000 г такого «золота» припадає 583 г чистого золота.

Задача 1. В яких пропорціях треба змішати 6%-ий і 9%-ий оцет, щоб отримати 8%-ий оцет.

Розв'язання. Застосуємо спосіб «рибки».

Креслимо «рибку».

                                    9 - 8=1 частину  для 6%-ого оцту

                                    8 - 6 = 2  частини для  9%-ого оцту.

 Отже, потрібно взяти одну частину 6%-ого оцту і дві частини 9%-ого.

Задача 2. В яких пропорціях треба змішати 50%-ий і 70%-ий розчин кислоти, щоб отримати 65%-ий розчин кислоти?

Розв'язання. При розв'язуванні таких задач на практиці можна користуватися стародавнім способом - «рибкою». Накреслимо таку схему.

У голові «рибки» запишемо потрібну концентрацію (65). Потім на верхньому і нижньому «плавниках» запишемо концентрації розчинів, які маємо. Потім навхрест (за стрілкою) обчислимо різниці (65 - 50 = 15 і 70 - 65 = 5). І як результат отримаємо співвідношення 5:15=1:3.

Задача 3. Скільки потрібно взяти рідини і скільки речовини, щоб отримати 100 г 20-процентного розчину?

Задача 4. В яких пропорціях треба змішати 50-процентний і 70-процентний розчини кислоти, щоб отримати 65%-ий розчин цієї кислоти?

Задача 5. В яких співвідношеннях треба сплавити золото 375-ої проби із золотом 750-ої проби, щоб отримати золото 500-ої проби?

Задача 6. Яку найбільшу кількість 9%-ого оцту можна отримати з 90 г 80-процентної оцтової есенції?

Задача 7. Скільки прісної води треба долити до 4 л морської, щоб зменшити вміст солі в ній у 2,5 рази?

Задача 8. Руда містить 40% домішок, а виплавлений з неї метал - 4%  домішок. Скільки металу отримаємо з 24 т руди?

Задача 9. У свіжому кавуні є 99% води. Після всихання вміст води становив 98%. У скільки разів всохся кавун?

Задача 10. Свіжі гриби містять 90% води. Визначте, у скільки разів всохлися гриби, якщо в стільки ж разів у них зменшився вміст води.

 

Колективне розв'язування задач.

Задачі на відсоткові розрахунки

 Задача 1. Із свіжих слив одержують 32 % сушених. Скільки взяли свіжих слив, якщо одержали 8 кг сушених?

         Розв'язання.

Складаємо відсоткову пропорцію:

100 % свіжих слив   - 32 % сушених слив.

100 кг свіжих слив  - 32 кг сушених слив,  

х кг свіжих слив   - 8 кг сушених слив.

Складаємо рівняння:

100 : х = 32 : 8,

32х=100∙8,

х=800:32,

х = 25.

Відповідь. 25 кг.

Задача 2. Плащ коштує 132 грн. Через деякий час його ціну підвищили на 5,28 грн. На скільки відсотків підвищилась ціна?

Розв'язання.

Складаємо відсоткову пропорцію:

132 грн. - 100 %,

5,28 грн. - х %.

Складаємо рівняння:

132 : 5,28 = 100 :х,

132х = 5,28 ∙100,

х = 528: 132,

х = 4.

Відповідь. На  4 %.

Задача 3. Маса деталі після обробки на токарному верстаті зменшилася з 6 кг до 4,2 кг. На скільки відсотків зменшилася маса деталі?

Задача 4. Коли фабрика випустила 204 пари взуття, то план був виконаний на 85 %. Скільки пар взуття мала випустити фабрика за планом?

Розв'язання.

Складаємо відсоткову пропорцію:

204 пари взуття - 85 %,

х  пар взуття - 100 %.

Складаємо рівняння:

204 : х = 85 : 100,

85х = 204∙100,

х = 20 400: 85,

х = 240.

Відповідь. 240 пар взуття.

Задача 5. Із 150 кг свіжих вишень одержали 36 кг сушених. Скільки відсотків сушених вишень виходить із свіжих?

Розв'язання.

Складаємо відсоткову пропорцію:

150 кг свіжих вишень - 100 %,

36 кг сушених вишень - х %.

Складаємо рівняння:

150:36=100:х,

150х = 36∙100,

х =3600: 150,

х =24.

Відповідь. 24 %.

 Задача 6. Коли цех випустив 360 деталей, то виконав 120 % місячного плану. Який місячний план цеху?

Розв'язання.

Складаємо відсоткову пропорцію:

360 деталей - 120 %,

х деталей - 100 %.

Тут х деталей становить місячний план цеху.

Складаємо рівняння:

360 : х = 120: 100,

120х = 360∙100,

х = 36 000: 120,

х = 300.

 Відповідь. 300 деталей.

Задача 7. 26 кг рису містять 19,5 кг крохмалю. Знайти відсотковий вміст крохмалю в рисі.

Розв'язання.

Складаємо відсоткову пропорцію:

26 кг рису   - 100 %,

19,5 кг крохмалю - х %.

Складаємо рівняння:

26 : 19,5 = 100 : х,

26х= 19,5 ∙100,

х= 1950: 26,

х = 75.

Відповідь. 75 %.

Задача 8. У процесі виготовлення силосу втрачається 12 % закладеної зеленої маси. Скільки одержать силосу із 450 т зеленої маси?

Розв'язання.

1.      Скільки відсотків становить силос?

100 % - 12 % = 88 %.

2.      Скільки одержали силосу із 450 т зеленої маси?

88% = 0,88;    450∙0,88 = 396 (т).

Відповідь. 396 т.

Задача 9. Комбайнер до обіду намолотив 21 т пшениці. Це становить 70 % пшениці, намолоченої ним за день. Скільки пшениці намолотив комбайнер після обіду?

Розв'язання.

1.      Скільки пшениці намолотив комбайнер за день?

70 % = 0,7;   

21 : 0,7 = 30 (т).

2.      Скільки пшениці намолотив комбайнер після обіду?

30 - 21 = 9 (т).

 Відповідь. 9 т.

Задача 10. Із 50 саджанців яблунь прийнялися 42 саджанці, а інші загинули. Скільки відсотків становлять саджанці, що загинули?

Розв'язання

1.      Скільки саджанців загинуло?

50 - 42 = 8 (садж.).

2.      Скільки відсотків становлять саджанці, що загинули?

8:50 = 0,16=16%.

Відповідь. 16 %.

Задача 11. Учні трьох класів посадили 340 дерев. Учні одного класу посадили 25 % усіх дерев, учні другого класу посадили 35 % дерев, а учні третього класу - решту. Скільки дерев посадили учні третього класу?

Розв'язання

1.      Скільки відсотків дерев посадили учні двох класів?

25 % + 35 % = 60 %.

2.      Скільки відсотків дерев посадили учні третього класу?

100 % - 60 % = 40 %.

3.      Скільки дерев посадили учні третього класу?

40 % = 0,4;   

 340 ∙ 0,4 = 136 (дер.).

 Відповідь. 136 дерев.

Задача 12. Велосипедист першого дня проїхав 34 % всієї траси, другого дня - 35 % всієї траси, а третього дня - решту 124 км. Яка довжина всієї траси?

Розв'язання.

1.      Скільки відсотків траси проїхав велосипедист за два дні?

34 % + 35 % = 69 %.

2.      Скільки відсотків траси проїхав велосипедист за третій день?

100 % - 69 % = 31 %.

3.      Яка довжина всієї траси?

31 % = 0,31;    

124 : 0,31 = 400 (км).

Відповідь. 400 км.

Задача 13. Периметр квадрата збільшився на 10%. На скільки відсотків збільшиться площа квадрата?

Розв'язання.     

Нехай а - сторона квадрата, тоді Р=4а - периметр, а якщо його периметр був збільшений на 10%, то нова сторона квадрата стала b = 1,1a, а тому площа збільшеного квадрата буде складати 1,21a∙a, тобто стане більшою на 21%.

Відповідь: на 21%.

Задача 14. У процесі виготовлення силосу втрачається 12 % закладеної зе­леної маси. Скільки одержать силосу із 450 т зеленої маси?

Розв'язання

1.      Скільки відсотків становить силос?

100 % - 12 % = 88 %.

2.      Скільки одержали силосу із 450 т зеленої маси?

88% = 0,88;    450-0,88 = 396 (т).

Відповідь. 396 т.

Задача 15. Із 50 саджанців яблунь прийнялися 42 саджанці, а інші загинули. Скільки відсотків становлять саджанці, що загинули?

Розв'язання

1.      Скільки саджанців загинуло?

50 - 42 = 8 (садж.).

2.      Скільки відсотків становлять саджанці, що загинули?

8:50 = 0,16=16%.

Відповідь. 16 %.

Колективне розв’язування:

1). Скільки заробили батько і мати за рік?

    2500∙12=30 000(грн.)

2). Скільки заплатили прибуткового податку?

    30 000∙0,13=3900 (грн.)

3). Скільки становить «чистий» заробіток, що пішов в бюджет родини?

    30 000-3900=26 100 (грн.)

4). Який прибуток отримано з акцій?

    50 000∙0,15=7500 (грн.)

5). Який прибуток з акцій після сплати податку?

    7500-7500∙0,3=7500-2250=5250 (грн.)

6). Який прибуток одержано по депозитних вкладах?

    70 000∙0,07=4900 (грн.)

7). Який прибуток по депозитних вкладах після сплати податку?

    4900-4900*0,05=4900-245=4655 (грн.)

8). Який річний прибуток?

    26100+5250+4655=36005 (грн.)

Задачі для  домашньої роботи

Задача 1. Зарплату токарю підвищили спочатку на 10%, а через рік ще на 20%. На скільки відсотків підвищилася зарплата порівняно з початковою?

Розв'язання.

Нехай зарплата токаря була а гривень. Після першого підвищення вона стала 1,1а, а після другого 1,2 ∙ (1,1а) = 1,32а

Отже, зарплата зросла на 32%.

Задача 2. Вологість свіжоскошеної трави 60%, а сіна - 15%. Скільки сіна можна отримати з однієї тонни свіжоскошеної трави?

Задача 3. Перше число становить 80% другого, друге - 40% третього, третє - 20% четвертого. Знайти ці числа, якщо їх сума 336.

Задача 4. За пересилку грошей беруть 2% від суми, що пересилається. Яку найбільшу суму можна переслати, маючи на руках 1000 гривень?

Задача 5. Книжка подорожчала на 25%, а потім подешевшала на 20%. Як змінилася ціна книжки порівняно з початковою?

Задача 6. Жіноче і чоловіче пальто мали однакову ціну. Жіноче подешевшало раз на 15% і ще раз на 15%, а чоловіче відразу на 30%. Яке пальто коштує зараз дорожче?

Задача 7. Продуктивність праці зросла на 40%. На скільки відсотків зменшиться час на виконання роботи?

Задача 8. В результаті рацпропозиції час на виготовлення деталі зменшився на 20%. На скільки відсотків зросла продуктивність праці?

Задача 9. Периметр квадрата збільшився на 10%. На скільки відсотків збільшиться площа квадрата?

Задача 10. Як зміниться площа прямокутника, якщо його довжину збільшити на 30%, а ширину зменшити на 30%?

Задача 11. Скільки води треба додати до 50 г 35% розчину, щоб отримати 10%-ий розчин?

Задача 12. Скільки 9%-ого оцту можна отримати з 90 г 80%-ої оцтової есенсії?

Задача 13. У свіжому кавуні 99% води. Після всихання вміст води становить 98%. У скільки разів всохся кавун?

Задача 14. Число збільшили на 25%. На скільки відсотків треба зменшити отримане число, щоб отримати дане число?

Задача 15. Знайти декілька натуральних чисел, які збільшуються на 20%, якщо їх цифри записати в оберненому порядку.

Задача 16. Хлопчик наскладав 5,2 гривні на купівлю фотоапарата. Решта грошей дали батько і два старших брати. Перший брат дав 25% суми без нього, другий - 33 х % суми без нього, а батько - 50% без нього. Скільки коштує фотоапарат?

Задача 17. Перша книжка на 50% дорожча, ніж друга. На скільки відсотків друга книжка дешевша, ніж перша?

Задача 18. Як зміниться величина дробу, якщо чисельник збільшити на 200%, а знаменник зменшити на 50%?

Задача 19. Зменшуване на 20% більше, ніж від'ємник. Скільки відсотків становить різниця від зменшуваного?

Задача 20. Руда містить 40% домішок, а виплавлений з неї метал - 4%. Скільки металу можна отримати з 24 т руди? (15 т)

Задача 21. Зі свіжих слив виходить 21% сушених. Скільки сушених слив можна отримати із 75 кг свіжих?

Задача 22. Перший тракторист зорав 40% поля, другий — 35% поля. Яку площу має поле, якщо перший зорав на 4 га більше, ніж другий?

Задача 23. Із 40 учасників шахового турніру 9 осіб мають звання гросмейстера. Який відсоток учасників турніру становлять гросмейстери?

Задача 24. Банк дав підприємцеві кредит 10 000 грн. зі ставкою 7% річних. Яку суму повинен повернути підприємець банкові через півроку?

Задача 25. Фермер минулого року зібрав у середньому по 30 ц зернових з 1 га, а в цьому році — по 32 ц. На скільки відсотків зросла урожайність зернових у цьому році порівняно з минулим роком?

Задачі для  колективної  роботи в навчальних групах

 1. У саду 140 дерев. Серед них 40 % яблунь, 25 % груш, а решта - сливи. Скільки слив росте в саду?

2. Три автомобілі перевезли 31,5 т вантажу. Другий автомобіль перевіз на 1,5 т вантажу більше, ніж перший, а третій - в 2 рази більше, ніж перший. Скільки тонн вантажу перевіз кожний автомобіль?

3. Площа поля 450 га. Першого дня зорали 33 % площі поля, другого дня - 35 %, а третього дня -  решту. Скільки гектарів поля зорали третього дня?

4. У трьох ящиках 70,5 кг груш. У першому ящику в 3 рази більше груш, ніж у другому, а в третьому - на 5,5 кг більше груш, ніж у другому. Скільки груш у кожному ящику?

5. Першого дня хлопчик прочитав 25 % книжки, другого -  32% . Після чого виявилося, що прочитана частина книжки на 21 сторінку більша за непрочитану. Скільки сторінок у книжці?

6. Площа чотирьох ділянок становить 136 га. Площі першої і четвертої діля­нок рівні, площа другої ділянки в 2 рази більша за площу першої, а площа третьої на 14 га менша за площу другої. Яка площа кожної ділянки окремо?

7. Вологість свіжої трави 70%,  висушеного сіна 12%. Скільки із однієї тони трави отримують сіна?

8. Морська вода містить 6% солі. Скільки прісної води треба долити до 50 кг морської, щоб вміст солі складав 1%?

9. Дві бригади разом повинні були виготовити згідно плану за місяць 680 деталей. Перша бригада перевиконала місячне завдання на 20%, а друга на 15%, отже поза планом обидві бригади виконали 100 деталей. Скільки за планом виготовляла кожна бригада?

10. В двох діжках було води порівно. Кількість води у першій діжці спочатку зменшилось на  20%, а згодом збільшилось на 20%. Кількість води у другій діжці спочатку збільшилось на 20%, а потім зменшилось на 20%. В якій діжці стало більше води?

11. На скільки відсотків зміниться площа прямокутника, якщо довжину збільшити на 20%, а ширину зменшити на 25%?

12. Число а складає 90% числа b, а  число  с складає 150% числа b. Знайти три  числа, якщо число с більше числа а на 72.

Задачі для самостійної роботи

1 варіант

1. У трьох шафах було 350 книжок. У першій шафі було 35 % всіх книжок, у другій - 45 % усіх книжок, а в третій - решта. Скільки книжок у третій шафі?

2. Із цистерни з пальним відлили спочатку 25 %, потім 35 % усього пального, після чого в цистерні залишилося 15 т пального. Скільки пального було в цистерні спочатку?

3. За 6 кг яблук і 4 кг груш заплатили 23 грн. 1 кг яблук на 0,5 грн. дорожчий за 1 кг груш. Скільки коштує 1 кг яблук та 1 кг груш?

4. У трьох сувоях 125 м шовку. В другому сувої в 2 рази більше шовку, ніж у першому, а в третьому - на 25 м більше, ніж у першому. Скільки метрів шовку в кожному сувої?

5. На перший автомобіль поклали в 3 рази менше вантажу, ніж на другий. Якщо на перший автомобіль добавити 3,3 т, а з другого зняти 1,5 т, то на автомобілях вантажу стане порівну. Скільки тонн вантажу було спочатку на кожному автомобілі?

2 варіант

1. У басейні купається 60 осіб. Серед них 20 % чоловіків, 30 % жінок, а решта - діти. Скільки дітей купається в басейні?

2. Бригада робітників першого дня відремонтувала 30 % шляху, другого дня 32 % усього шляху, а третього дня - решту 19 км. Скільки кілометрів шляху відремонтувала бригада за три дні?

3. За 5 кг цукерок і 4 кг печива заплатили 72,6 грн. 1 кг печива на 0,6 грн. дорожчий за 1 кг цукерок. Скільки коштує 1 кг цукерок і 1 кг печива?

4. У трьох кошиках 120 кг огірків. У першому в 4 рази більше, ніж у другому, а в третьому на 24 кг більше, ніж у другому. Скільки огірків у кожному кошику?

5. У першому бідоні було в 2,5 раза менше молока, ніж у другому. Якщо в перший бідон  долити 18,25 л молока, а з другого вилити 6,5 л молока, то в обох бідонах молока стане порівну. Скільки літрів молока було в кожному бідоні спочатку?

3 варіант

1. За три дні туристи пройшли 75 км. Першого дня вони пройшли 35 % шляху, а за другий день 37 % усього шляху. Скільки кілометрів пройшли туристи за третій день?

2. Учні першого дня зібрали 25 % макулатури, другого дня 30 % усієї макулатури, а третього дня - решту 216 кг макулатури. Скільки макулатури зібрали учні за три дні?

3. За 4 кг помідорів і 7 кг огірків заплатили 22,5 гри. 1 кг помідорів дорожчий за 1 кг огірків на 1,5 грн. Скільки коштує 1 кг помідорів і 1 кг огірків?

4. У трьох букетах було 75 троянд. У першому букеті було на 3 троянди більше, ніж у третьому, в другому букеті в 2 рази більше квітів, ніж у третьому. Скільки троянд у кожному букеті?

5. У першому кошику було в 3 рази більше слив, ніж у другому. З першого кошика забрали 8,3 кг слив, а в другий добавили 4,5 кг. Тоді в кошиках слив стало порівну. Скільки слив було в кожному кошику спочатку?

4 варіант

1. За три дні зорали 250 га поля. За перший день зорали 37 % площі, а за другий день - 32 % площі поля. Скільки гектарів зорали за третій день?

2. За перший місяць витратили 35 % завезеного для опалення вугілля, за другий місяць - 40% усього вугілля, а за третій - решту 32 т. Скільки вугілля завезли для опалення?

3. Купили 3 кг ковбаси і 2 кг сиру. За всю покупку заплатили 76,5 грн. 1 кг сиру на 2 грн. дорожчий за 1 кг ковбаси. Скільки коштує 1 кг ковбаси та 1 кг сиру?

4. У трьох посудинах було 42 л мастила. В першій посудині було в 3 рази більше мастила, ніж у другій, а в третій - на 7 л більше, ніж у другій. Скільки літрів мастила було в кожній посудині?

5. У першій цистерні було в 1,5 раза більше бензину, ніж у другій. Якщо з першої цистерни вилити 2,5 т, а в другу долити 7,5 т бензину, то в обох цистернах бензину стане порівну. Скільки бензину було в кожній цистерні спочатку?

5 варіант

1. У саду 800 фруктових дерев. 56 % усіх дерев становлять яблуні, 25 % усіх яблунь посадили діти. Скільки яблунь посадили діти?

2. Першого дня зорали 23 % всього поля, другого дня - ¼ поля, третього - 22 % всього поля, а за четвертий день зорали решту 99 га поля. Скільки гектарів поля зорали за чотири дні?

3. Вантажний автомобіль з причепом перевозить за одну поїздку на 3 т зерна більше, ніж вантажний автомобіль без причепа. Тому вантажний автомобіль з причепом за 6 поїздок перевіз на 8 т зерна більше, ніж автомобіль без причепа за 7 поїздок. Скільки тонн зерна перевозить кожний автомобіль за одну поїздку?

4. Учні трьох класів зібрали 646 кг макулатури. Учні одного класу зібрали на 20 кг макулатури більше, ніж учні другого, а учні першого і другого зібрали разом на 18 кг більше, ніж учні третього. Скільки кілограмів макулатури зібрали учні кожного класу?

5. Два хлопчики виміряли кроками довжину однієї й тієї самої ділянки шосе. Перший хлопчик зробив при вимірюванні на 20 кроків менше, ніж другий. Довжина кроку першого хлопчика дорівнює 0,55 м, а другого 0,5 м. Знайти довжину вимірюваної ділянки шосе.

6 Варіант.

1. Вологість свіжої трави 60%,  висушеного сіна 15%. Скільки із однієї тони трави отримують сіна?

2. Морська вода містить 5% солі. Скільки прісної води треба долити до 40 кг морської, щоб вміст солі складав 2%?

3. Дві бригади разом повинні були виготовити згідно плану за місяць 680 деталей. Перша бригада перевиконала місячне завдання на 20%, а друга на 15%, отже поза планом обидві бригади виконали 118 деталей. Скільки за планом виготовляла кожна бригада?

4. В двох діжках було води порівно. Кількість води у першій діжці спочатку зменшилось на  10%, а згодом збільшилось на 10%. Кількість води у другій діжці спочатку збільшилось на 10%, а потім зменшилось на 10%. В якій діжці стало більше води?

5. На скільки відсотків зміниться площа прямокутника, якщо довжину збільшити на 30%, а ширину зменшити на 15%?

6. Число а складає 80% числа b, а  число  с складає 140% числа b. Знайти  числа, якщо число с більше числа а на 72.

 

 

Самостійна робота

1 варіант

1.     Знайти 15% від числа 120.
2.     Знайти число, 11% якого складає 121.
3.     Скільки відсотків складає число від 21?
4.     На міську олімпіаду з математики з усіх шкіл приїхало 140 учнів, що становить 3,5% усіх бажаючих взяти участь в олімпіаді. Скільки всього учнів хотіли стати учасниками олімпіади?
5.     Позичальник отримав кредит на суму 2000 грн під 13 % річних. Через 140 днів кредит було повністю погашено. Розрахуйте, яку суму позичальник віддав банку? На скільки різниться ця сума від позиченої?

2 варіант

1.     Знайти 29% від числа 580.
2.     Знайти число, 15% якого складає 380.
3.     Скільки відсотків складає число 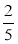від 25?
4.     У фіналі математичної олімпіади взяли участь 160 учнів, із них 24 стали призерами. Який відсоток учнів став призерами олімпіади?
5.     Вкладник поклав в банк 20.000грн. під 12% річних. Які відсоткові гроші він матиме через 2 років?

3 варіант

1.     Знайти 23% від числа 690.
2.     Знайти число, 12% якого складає 600.
3.     Скільки відсотків складає число 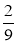від 18?
4.     Із свіжих слив одержують 32 % сушених. Скільки взяли свіжих слив, якщо одержали 8 кг сушених?
5.     Вкладник поклав в банк 10.000грн. під 21% річних. Які відсоткові гроші він матиме через 3 років?

4 варіант

1.     Знайти 21% від числа 840.
2.     Знайти число, 12% якого складає 840.
3.     Скільки відсотків складає число 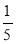від 25?
4.     Коли фабрика випустила 204 пари взуття, то план був виконаний на 85 %. Скільки пар взуття мала випустити фабрика за планом?
5.     В ощадний банк поклали 10000 гри. Через рік сума вкладу дорівнювала 19905 гри. Під який відсоток покладено вклад?

5 варіант

1.     Знайти 30% від числа 120.
2.     Знайти число, 25% якого складає 625.
3.     Скільки відсотків складає число 0,5 від 20?
4.     Плащ коштує 132 грн. Через деякий час його ціну підвищили на 5,28 грн. На скільки відсотків підвищилась ціна?
5.     Вкладник поклав в банк 10.000грн. під 4% річних. Які відсоткові гроші він матиме через 5 років?

6 варіант

1.     Знайти 20% від числа 180.
2.     Знайти число, 15% якого складає 60.
3.     Скільки відсотків складає число 0,2 від 20?
4.     Із 150 кг свіжих вишень одержали 36 кг сушених. Скільки відсотків сушених вишень виходить із свіжих?
5.     Вкладник розмістив суму розміром 2600 грн. в банк. Визначте, яку суму отримає вкладник через 4 роки, якщо відсоткова ставка складає 15% в рік.

7 варіант

1.     Знайти 24% від числа 120.
2.     Знайти число, 12% якого складає 720.
3.     Скільки відсотків складає число 0,5 від 20?
4.     Коли цех випустив 360 деталей, то виконав 120 % місячного плану. Який місячний план цеху?
5.     Позичальник отримав кредит на суму 15000 грн під 30 % річних. Через 200 днів кредит було повністю погашено. Розрахуйте, яку суму позичальник віддав банку? На скільки різниться ця сума від позиченої?

8 варіант

1.     Знайти 20% від числа 120.
2.     Знайти число, 24% якого складає 480.
3.     Скільки відсотків складає число 0,6 від 120?
4.     26 кг рису містять 19,5 кг крохмалю. Знайти відсотковий вміст крохмалю в рисі.
5.     В ощадний банк поклали 8000 гри. Через рік сума вкладу дорівнювала 19045 гри. Під який відсоток покладено вклад?

9 варіант

1.     Знайти 20% від числа 120.
2.     Знайти число, 12% якого складає 60.
3.     Скільки відсотків складає число 0,3 від 20?
4.     У процесі виготовлення силосу втрачається 12 % закладеної зеленої маси. Скільки одержать силосу із 450 т зеленої маси?
5.     Вкладник поклав до банку 1000 грн. під 3% річних. Який нарощений капітал буде у вкладника через три роки?

10 варіант

1.     Знайти 20% від числа 120.
2.     Знайти число, 12% якого складає 60.
3.     Скільки відсотків складає число 0,3 від 20?
4.     Зарплату токарю підвищили спочатку на 10%, а через рік ще на 20%. На скільки відсотків підвищилася зарплата порівняно з початковою?\
5.     Вкладник поклав до банку 3000грн під 5% річних. Який нарощений капітал буде у вкладника через 6 роки?

11 варіант

1.     Знайти 20% від числа 120.
2.     Знайти число, 12% якого складає 60.
3.     Скільки відсотків складає число 0,3 від 20?
4.     Книжка подорожчала на 25%, а потім подешевшала на 20%. Як змінилася ціна книжки порівняно з початковою?
5.     Банк дав підприємцеві кредит 10 000 грн. зі ставкою 7% річних. Яку суму повинен повернути підприємець банкові через півроку?

12 варіант

1.     Знайти 20% від числа 120.
2.     Знайти число, 12% якого складає 60.
3.     Скільки відсотків складає число 0,3 від 20?
4.     Площа земельної ділянки 84 га, 75% її вже зорали. Скільки гектарів ділянки землі залишилось зорати?
5.     В ощадний банк поклали 9000 гри. Через рік сума вкладу дорівнювала 9945 гри. Під який відсоток покладено вклад?

13 варіант

1.     Знайти 20% від числа 120.
2.     Знайти число, 12% якого складає 60.
3.     Скільки відсотків складає число 0,3 від 20?
4.     За три дні машина проїхала 300 км. За перший день вона пройшла 30% шляху, за другий день – 35% шляху, за третій день – залишок шляху. Скільки кілометрів пройшла машина за третій день?
5.     Банк дав підприємцеві кредит 10 000 грн. зі ставкою 7% річних. Яку суму повинен повернути підприємець банкові через півроку?

14 варіант

1.     Знайти 30% від числа 120.
2.     Знайти число, 12% якого складає 480.
3.     Скільки відсотків складає число 0,3 від 30?
4.     Одне число дорівнює 120, друге складає 50 % від першого, третє – 25 % від другого. Знайти середнє арифметичне цих чисел.
5.     Вкладник поклав в банк 20.000грн. під 7% річних. Які відсоткові гроші він матиме через 5 років?

15 варіант

1.     Знайти 20% від числа 120.
2.     Знайти число, 12% якого складає 60.
3.     Скільки відсотків складає число 0,3 від 20?
4.     Периметр прямокутника 180 см. Знайти сторони прямокутника, якщо одна з них на 20% менше , ніж друга.
5.     При несвоєчасній сплаті боргів нараховують 4% пені за кожний день просрочення. Яку суму потрібно заплатити через 18 днів після строку погашення 600 грн. боргу?

16 варіант

1.     Знайти 40% від числа 160.
2.     Знайти число, 12% якого складає 84.
3.     Скільки відсотків складає число 0,5 від 20?
4.     Різниця двох чисел дорівнює 72. Знайти ці числа, якщо 4,5 % від одного з них дорівнює 8,5 % другого.
5.     Вкладник розмістив суму розміром 2000 грн. в банк. Визначте, яку суму отримає вкладник через 7 роки, якщо відсоткова ставка складає 13% в рік.

 

 

 

 Контрольне  оцінювання з теми  «Відсоткові  розрахунки»

 Варіант - 1.

1.     Знайти 15% від числа

(1+5/7)∙0,625:(2/7) + ( (1,5)3- 0,75):2,1 + (0,625∙32∙2,7/(8,1∙1,6∙2,5).

А) 6+ 2/3;             Б) 1;           В) 5;              Г) 6;   Д) інша відповідь.

2. Туристи пройшли маршрут за три дні За перший день вони пройшли 35% від усього шляху,  а за другий - 20% того, що залишилось. Скільки відсотків від усього шляху їм залишилося  пройти за третій день?

А) 52%;        Б) 45%;       В) 48%;           Г) 48%;  Д) інша відповідь.

3. Скільки буде, якщо 6х збільшити на 200/66?

А) 12х;          Б) 24х;       В) 18х;             Г) 10х;   Д) інша відповідь.

4. Довжина прямокутника  в 2 рази більша за ширину. Довжину зменшили на 40%, а ширину збільшили на 40% .  На скільки відсотків в порівнянні з початковою змінилась площа прямокуника?

А) зменшилась на 16%;       Б) зменшилась на 12%;  В) збільшилась на 16%;                    Г) збільшилась на 12%;  Д) інша відповідь.

5. Є два розчини вагою 80 г і 120 г.   В першому розчині  міститься  12 г  солі, а в другому - 15 г солі. Якою буде концентрація розчину, якщо змішати обидва розчини?

А) 15%;        Б) 13.5%;    В) 13.2%;      Г)27%;  Д) інша відповідь.

6. Товар коштував 10 грн.  Через рік його уцінили на х%.   Скільки гривень став коштувати товар?

А) 0,9х грн;             Б) 9,1х грн;       В) (10 - 0,1х) грн;      Г) 9,01х грн;  Д) інша відповідь.

7. На скільки відсотків збільшилась величина, якщо вона збільшилась в 1,5раза?

А) на 20%;  Б) на 150%;     В) на 50%;      Г) на 103%.  Д) інша відповідь.

8. Скільки можна отримати 24%-ного соляного розчину з 96г солі?

А) 0, 4 кг;      Б) 120 г;    В) 240 г;      Г) 0,14 кг;  Д) інша відповідь.

9.  3 Вінниці до Києва вирушив легковий автомобіль зі швидкістю 90 км/год. А з Києва до Вінниці одночасно з автомобілем вирушив автобус, зі швидкістю 60 км/год. Хто з них в момент зустрічі ближче до Києва і хто з них ближче до Вінниці?

А) автобус ближче до Києва, автомобіль ближче до Вінниці;      В) на однаковій відстані;   Б) автобус ближче до Вінниці, автомобіль ближче до Києва; Д) інша відповідь.

10.  Дві третини  шляху на 60 км більше, ніж 20% від залишку. Якої довжини весь шлях?

А) 120 км;  В) 490 км;  Б) 200 км;   Г) 100 км;  Д) інша відповідь.

11. Букіністичний магазин купив книгу на 20% дешевше номіналу, а продав по номіналу. Скільки   відсотків прибутку він одержав?

А) 20%;      Б) 80%;    В) 40% ;        Г)25%;   Д) інша відповідь.

12. Вкладник приніс в банк 10 грн під 2% річних, а скільки грошей буде на рахунку через два роки?

А) 10 грн 40 коп;   Б) 10 грн 20 коп;    В) 10,4 грн;     Г) 10,404 грн; Д) інша відповідь.

Контрольне  оцінювання з теми  «Відсоткові  розрахунки»

Варіант 2

1.     Знайти 40% від числа

(1/2+3/4)∙0,625:(1/4) + ( (1,5)3 - 0,75 ):2,1 + (0,625∙32∙2,7/(8,1∙1,6∙2,5).

А) 2,5;  Б) 12;  В) 9;   Г) 3,6; Д) інша відповідь.

2. На полиці книг з історії на 40% менше, ніж книг з літератури.    На скільки відсотків книг  з літератури більше, ніж книг з історії?

А) на 200/66 %;     Б) на 60%;    В) на 40%;        Г)на 100/3 %; Д) інша відповідь.

3. Скільки було, якщо при збільшенні на 25% стало 5х?

А)5х;    Б)4х;    В)5,25х;    Г) 0,5х.  Д) інша відповідь.

4. До 200 г 15%-го розчину додали ще 300г 40%-го розчину цієї ж речовини. Якої концентрації розчин отримають?

А) 45%;     Б) 35%;    В) 28%;    Г) 30%; Д) інша відповідь.

5. На скільки відсотків в порівнянні з початковою   змінилась   температура повітря, якщо вона спочатку підвищилась на 25%, а потім знизилась на 40%?

А) підвищилась на 25%; Б) підвищилась на 20%; В)знизилась на 75%; Г) знизилась на 25%;  Д) інша відповідь.

6. Морська   вода   містить    5%   солі. Скільки кілограмів води треба випарувати із 80кг морської води, щоб концентрація солі в ній збільшилась до 20%?

А) 60 кг;     Б) 20 кг;    В) 40 кг;     Г) 55,5 кг;  Д) інша відповідь.

7. Число А складає від числа В  140%. У скільки рази число А більше за число В?

А) в 0.14 раза;   Б) в 2/7 рази;     В) в 0,6 раза;      Г) в 1.4 рази;   Д) інша відповідь.

8. На овочевій базі при першому сортуванні овочів втрати складали 5%, а при повторному - 4%,   після чого на базі залишилось 54,72 т овочів. Скільки овочів було завезено на базу?

А) 60 т;  Б) 65 т;  В) 55 т;   Г) 100т;  Д) інша відповідь.

9. Собака і хлопчик разом вирушили до отари, яку випасали на полонині. Хлопчик іде із швидкістю 5 км/год, а собака біжить із швидкістю в 2 рази більшою. Яку відстань пробігла собака за той час, що хлопчик йшов до отари, якщо собака весь час бігав від хлопчика до отари і назад, а хлопчик йшов 0,5 год?

А) 5 км;      Б) 10 км;   В) 2,5 км;     Г) 20 км;   Д) інша відповідь.

10. Знайти число, якщо 45% від цього числа на 0,7 більше, ніж  третина від цього числа.

А) 0,7;   Б) 60;  В) на 80%;  Г) на 180%;   Д) інша відповідь.

11.  Один доданок в 1,5 раза більший за другий. На скільки відсотків зміниться сума, якщо перший доданок зменшити в 3 рази, а другий збільшити на 50%?

А) зменшиться на 50% ; Б) збільшиться на 50%;  В) зменшиться на 20% ; Г) збільшиться на 20%;   Д) інша відповідь.

12. Число А складає від числа В   20%.   На скільки відсотків треба збільшити число А, щоб отримати число  В?

А) на 80%;  Б) на 180%;  В)на 200%;   Г) на 400%;  Д) інша відповідь.

Знаходження відсотків від числа

1.   Площа земельної ділянки 84 га, 75% її вже зорали. Скільки гектарів ділянки землі залишилось зорати?
2.   Із свіжих яблук отримали 18% сушених. Скільки сушених яблук отримають із 250 кг свіжих ?
3.   За три дні машина проїхала 300 км. За перший день вона пройшла 30% шляху, за другий день – 35% шляху, за третій день – залишок шляху. Скільки кілометрів пройшла машина за третій день?
4.   Одне число дорівнює 120, друге складає 50 % від першого, третє – 25 % від другого. Знайти середнє арифметичне цих чисел.
5.   Периметр прямокутника 180 см. Знайти сторони прямокутника, якщо одна з них на 20% менше , ніж друга.
6.   Перший тракторист зорав 40 % поля, а другий зорав 35 % поля. Чому дорівнює площа всього поля, якщо перший зорав на 4 га більше?
7.   Різниця двох чисел дорівнює 72. Знайти ці числа, якщо 4,5 % від одного з них дорівнює 8,5 % другого.

Знаходження відсотків від числа

№1 Площа земельної ділянки 84 га, 75% її вже зорали. Скільки гектарів ділянки землі залишилось зорати?

Розв’язання.

1) 84: 100 • 75 = 63 (га) – вже зорали;

2) 84 – 63 = 21 (га) – залишилось зорати.

Відповідь: 21га

№2 Із свіжих яблук отримали 18% сушених. Скільки сушених яблук отримають із 250 кг свіжих ?

Розв’ язання.

250 : 100 • 18 = 45 ( кг) – отримали сушених яблук

Відповідь: 45кг

№3 За три дні машина проїхала 300 км. За перший день вона пройшла 30% шляху, за другий день – 35% шляху, за третій день – залишок шляху. Скільки кілометрів пройшла машина за третій день?

Розв’язання.

1) 300 : 100 • 30 = 90 (км) – пройшла машина за перший день;

2) 300 : 100 • 35 = 105 (км) – пройшла машина за другий день;

3) 300 – ( 90 + 105) = 105 ( км) – пройшла машина за третій день.

Відповідь: 105 км

№4 Одне число дорівнює 120, друге складає 50 % від першого, третє – 25 % від другого. Знайти середнє арифметичне цих чисел.

Розв’язання.

1) 120 • = 60 – друге число;

2) 60 • = 15 – третє число;

3) ( 120 + 60 + 15 ) : 3 65 – середнє арифметичне цих чисел.

Відповідь : 65

№5 Периметр прямокутника 180 см. Знайти сторони прямокутника, якщо одна з них на 20% менше , ніж друга.

Розв’язання.

В С Нехай сторона АD прямокутника АВСD

дорівнює Х см, тоді сторона АВ , яка

менше на 20 % від АD дорівнює 0,8 Х см

А D ( Х : 100 • 20 = 0,2 Х; Х – 0,2Х = 0,8 Х).

Периметр прямокутника дорівнює Р = 2 ( а + в ), за умовою задачі – 180 см.

Складемо і розв’яжемо рівняння:

( Х + 0,8 Х) = 180

1,8 Х = 180 : 2

1,8 Х = 90

Х = 90 : 1,8

Х = 50

Тоді АD = ВС = 50 см, АВ = СD = 50 •0,8 = 40 см.

Відповідь : 50см, 40см.

№6 Перший тракторист зорав 40 % поля, а другий зорав 35 % поля. Чому дорівнює площа всього поля, якщо перший зорав на 4 га більше?

Розв’язання.

Нехай площа всього поля дорівнює Х га. Тоді перший тракторист зорав 0,4 Х га ( Х : 100 • 40 = 0,4 Х), а другий – 0,35 Х га, що на 4 га менше, ніж перший. Складемо і розв’яжемо рівняння:

0,4 Х – 0,35 Х = 4

0,05 Х = 4

Х = 4 : 0,05

Х = 80

Тоді площа всього поля дорівнює 80 га, перший тракторист зорав 0,4• 80 = 32 га, а другий – 0,35 • 80 = 28 га.

Відповідь : 80 га

№7 Різниця двох чисел дорівнює 72. Знайти ці числа, якщо 4,5 % від одного з них дорівнює 8,5 % другого.

Розв’язання.

Нехай перше число дорівнює Х, тоді друге – ( Х – 72). 4,5 % від першого дорівнює Х : 100 • 4,5 = 0,045Х, а 8,5 % від другого - ( Х – 72) : 100 • 8,5 = 0,085( Х – 72). Отримані числа рівні між собою. Складемо і розв’яжемо рівняння:

0,045Х = 0,085( Х- 72)

0,045Х = 0,085Х – 6,12

- 0,04Х = - 6,12

0,04Х = 6,12

Х = 6,12 : 0,04

Х = 153

Тоді перше число дорівнює 153, а друге число – 81.

Відповідь : 153 і 81. 

Знаходження числа за його відсотками

1. За планом тракторист повинен був зорати поле. Він зорав 2 га, що становить 75 % поля. Чому дорівнює площа всього поля ?
2.   Комбайнер перевиконав завдання на 15% і зібрав зернові з площі 230 га. Скільки гектарів за планом йому треба було обробити ?
3.        Із свіжих груш виходить 18 % сушених. Скільки було взяти свіжих, щоб отримати 45 кг сушених ?
4.        Велогонщик в перший день пройшов 35 % довжини всієї траси, в другий день – 37 % всієї траси, а в третій день – останні 140 км. Яка довжина всієї траси ?
5.        В коробці були кольорові олівці. Спочатку з коробки взяли 50 % олівців, потім – 40 % залишку. Після цього в коробці залишилось 3 олівця. Скільки олівців було в коробці ?
6.        Бригада теслярів використала на ремонт будівлі 4,2 м³ дошок. При цьому вона зекономила 16 % виділених для ремонту дошок. Скільки кубічних метрів дошок було виділено для ремонту будівлі?
7.        Свіжі гриби містять 90 % води, а сушені – 12 % води. Скільки сушених грибів отримають із 20 кг свіжих ?

Знаходження числа за його відсотками

№1 За планом тракторист повинен був зорати поле. Він зорав 2 га, що становить 75 % поля. Чому дорівнює площа всього поля ?

Розв̒язання.

1) 2 : 75 • 100 = = = 2 ( га) – площа всього поля

Відповідь : 2 га

№2 Комбайнер перевиконав завдання на 15% і зібрав зернові з площі 230 га. Скільки гектарів за планом йому треба було обробити ?

Розв̒язання.

1) Нехай 100 % - це план, тоді комбайнер виконав 100 + 15 = 115 ( % ) від плану.

2) 230 : 115 • 100 = 200 ( га) – треба було обробити за планом.

Відповідь : 200 га

№3 Із свіжих груш виходить 18 % сушених. Скільки було взяти свіжих, щоб отримати 45 кг сушених ?

Розв̒язання.

1) Нехай 100 % становить вага свіжих груш,

2) 45 : 18 • 100 = 250 ( кг) – свіжих груш треба взяти.

Відповідь : 250 кг

№4 Велогонщик в перший день пройшов 35 % довжини всієї траси, в другий день – 37 % всієї траси, а в третій день – останні 140 км. Яка довжина всієї траси ?

Розв̒язання.

1) Нехай 100 % - довжина всієї траси,

2) 35 + 37 = 62 (  – пройшов велогонщик за два дні,

3) 100 – 62 = 28 ( % ) – пройшов велогонщик за третій день,

4) 140 : 28 • 100 = 500 ( км ) – довжина всієї траси.

Відповідь : 500 км

№5 В коробці були кольорові олівці. Спочатку з коробки взяли 50 % олівців, потім – 40 % залишку. Після цього в коробці залишилось 3 олівця. Скільки олівців було в коробці ?

Розв̒язання.

1) Нехай в коробці лежало 100 % кольорових олівців,

2) 100 – 50 (  – олівців залишилось в коробці після того, як взяли 1 раз,

3) 40 % від 50 % = 50 : 100 •40 = 20 % - олівців взяли з коробки 2 раз,

4) 50 – 20 = 30 (  – олівців залишилось в коробці після того, як взяли

2 раз ,

5) 30 % від Х дорівнює 3 олівцям, (Х - всього олівців у коробці), Складемо і розв’яжемо рівняння:

0,3Х = 3

Х = 3 : 0,3

Х = 10

Тоді, в коробці було 10 олівців.

Відповідь : 10 олівців

№6 Бригада теслярів використала на ремонт будівлі 4,2 м³ дошок. При цьому вона зекономила 16 % виділених для ремонту дошок. Скільки кубічних метрів дошок було виділено для ремонту будівлі ?

Розв̒язання.

1) Нехай 100 % дошок треба виділити на ремонт будівлі,

2) 100 – 16 = 84 (%) – дошок пішло на ремонт будівлі,

3) 4,2 м³ складає 84 % , тоді 84 % від Х дорівнює 4,2 м³,

Складемо і розв’яжемо рівняння:

0,84Х = 4,2

Х = 4,2 : 0,84

Х = 5

Тоді 5 м³ дошок було виділено на ремонт будівлі.

Відповідь : 5 м³

№7 Свіжі гриби містять 90 % води, а сушені – 12 % води. Скільки сушених грибів отримають із 20 кг свіжих ?

Розв̒язання.

Свіжі та сушені гриби містять воду та суху речовину ( мікроелементи, клітковина, білки, жири, вуглеводи та інше). Нехай свіжих грибів взяли 100%, що становить 20 кг за умовою задачі. Тоді сухої речовини вони містять 100- 90 = 10 (%), або 20 : 100 •10 = 2 (кг). При висиханні свіжі гриби втрачають вологу, а зміст сухої речовини не змінюється. Отже нехай тепер 100% становить вага сушених грибів, із яких 12% - це вода, тоді 100 – 12 = 88 (%) це – суха речовина грибів.

Знайдемо вагу сушених грибів :

2 : 88 • 100 = 2 кг

Відповідь : 2 кг

Знаходження відсоткового відношення

1.        У класі навчається 30 учнів, серед яких - 21 дівчинка. Скільки відсотків дівчат навчається в цьому класі ?
2.        За два дні турист пройшов 50 км. За перший день він пройшов 30 км. Скільки відсотків шляху йому залишилось пройти?
3.        За планом робочий повинен був виготовити 200 деталей, а він виготовив 220 деталей. На скільки відсотків він виконав план ? На скільки відсотків він перевиконав план ?
4.        В 450 г розчину міститься 27г солі. Знайти відсоток солі в цьому розчині.

Знаходження відсоткового відношення

№1 У класі навчається 30 учнів, серед яких - 21 дівчинка. Скільки відсотків дівчат навчається в цьому класі ?

Розв̒язання.

Кількість дівчат у класі становить

• 100% = 70%

Відповідь : 70%

№2 За два дні турист пройшов 50 км. За перший день він пройшов 30 км. Скільки відсотків шляху йому залишилось пройти ?

Розв̒язання.

Нехай весь шлях становить 100%

1) • 100% = 60% - пройшов турист за перший день;

2) – залишилось пройти туристу.

Відповідь : 40%

№3 За планом робочий повинен був виготовити 200 деталей, а він виготовив 220 деталей. На скільки відсотків він виконав план ? На скільки відсотків він перевиконав план ?

Розв̒язання .

Нехай план становить 100%. Тоді робітник, який виготовив 220 деталей , виконав план на

• 100% = 110%

Він перевиконав план на 110 – 100 = 10 (%).

Відповідь: 110%, 10%.

№4 В 450 г розчину міститься 27г солі. Знайти відсоток солі в цьому розчині.

Розв̒язання.

Відсоток солі, яка міститься в розчині знайдемо так :

• 100% = 6%

Відповідь : 6%