ДПА з математики для 9 класу
Завдання для державної підсумкової атестації з математики в 9 класі складаються з 10 варіантів атестаційних робіт. Завдання складала, використовуючи завдання різних збірників та різних років.
Кожен варіант складається з трьох частин, які відрізняються за складністю та формою тестових завдань.
Завдання складала з метою запобігання списування з розв'язників. Тут розв'язувати потрібно самостійно!!
Пояснювальна записка
Завдання для державної підсумкової атестації з математики в 9 класі складаються з 10 варіантів атестаційних робіт.
Кожен варіант складається з трьох частин, які відрізняються за складністю та формою тестових завдань.
У першій частині пропонується 12 завдань з вибором однієї правильної відповіді (8завдань з алгебри і 4 завдання з геометрії). Для кожного тестового завдання подано 4 варіанти відповіді, з яких тільки один правильний. Завдання першої частини вважається виконаним, якщо в бланку відповідей указана тільки одна літера, якою позначена правильна відповідь. Правильне розв’язання кожного завдання №№ 1.1 – 1.12 оцінюється одним балом.
Друга частина атестаційної роботи складається з 6 завдань ( 4 завдання з алгебри і 2 завдання з геометрії) відкритої форми з короткою відповіддю. Таке завдання вважається виконаним правильно, якщо в бланку відповідей записана правильна відповідь (число, вираз, корені рівняння тощо). Усі необхідні обчислення учні роблять у чернетках. Правильне розв’язання кожного завдання №№ 2.1 -2.6 оцінюється двома балами.
Третя частина атестаційної роботи складається з 4 завдань ( 3 завдання з алгебри і 1 завдання з геометрії) відкритої форми з розгорнутою відповіддю. Завдання третьої частини вважаються виконаними правильно, якщо учень навів розгорнутий запис розв’язування завдання з обґрунтуванням кожного етапу та дав правильну відповідь. Правильне розв’язання кожного з завдань №№ 3.1 – 3.4 оцінюється чотирма балами.
Система нарахування балів за правильне виконання завдання для оцінювання робіт наведено в табл..1
|
Номер завдання |
Кількість балів |
усього |
|
1.1 – 1.12 |
По 1 балу |
12 балів |
|
2.1 – 2.6 |
По 2 бали |
12 балів |
|
3.1 – 3.4 |
По 4 бали |
16 балів |
|
Усього балів |
|
40 балів |
Відповідність кількості набраних балів учнем оцінці за 12-ти бальною системою оцінювання навчальних досягнень учнів наведено в табл..2
|
Кількість набраних балів |
Оцінка за 12-ти бальною системою |
|
1 - 2 |
1 |
|
3 - 4 |
2 |
|
5 - 6 |
3 |
|
7 - 9 |
4 |
|
10 - 12 |
5 |
|
13 - 16 |
6 |
|
17 - 20 |
7 |
|
21 -24 |
8 |
|
25 -28 |
9 |
|
29 -32 |
10 |
|
33 -36 |
11 |
|
37 -40 |
12 |
Варіант 1
Частина перша
Завдання 1.1-1.12 мають по чотири варіанти відповідей, з яких тільки одна відповідь правильна. Оберіть правильну, на вашу думку, відповідь та позначте її у бланку відповідей.
- Спростіть вираз: 6b – (3b – 1).
-
9b – 1; Б) 3b + 1; В) 3b – 1; Г) 9b +1.
-
Якому одночлену дорівнює вираз (
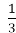 m6)3 ?
m6)3 ?
-
Якому одночлену дорівнює вираз (
А)![]() m18; Б)
m18; Б) ![]() m9; В)
m9; В) ![]() m18; Г)
m18; Г) ![]() m9.
m9.
1.3 Розв’яжіть нерівність 7x +8 ≤ − 6.
А) х ≤ 2; Б) х ≤ −2; В) х ≥ 2; Г) х ≥ − 2.
1.4. Обчисліть значення виразу (3 −![]() )(3+
)(3+![]() ).
).
А) −2; Б) 8; В) 14; Г) 4.
1.5. Скоротіть дріб ![]()
А)![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
1.6. Знайдіть корені рівняння 4х2 – 5х+1=0.
А) 1;![]() ; Б) −2; −
; Б) −2; − ![]() ; В) −1; −
; В) −1; −![]() ; Г) 2;
; Г) 2; ![]() .
.
1.7. Через яку з даних точок проходить графік функції у= 2х2 – 1 ?
А) А(−3; −19); Б) В(−3; 11); В) С(−3;17); Г) Д(−3; −17).
1.8. Чому дорівнює четвертий член геометричної прогресії, перший член якої
b1 = 3, а знаменник q = −2 ?
А) −18; Б)18; В) 24; Г) −24.
1.9. Чому дорівнює площа трикутника, периметр якого становить 12 см, а
радіус вписаного кола дорівнює 4 см?
А) 12 см2; Б) 16 см2; В) 24 см2; Г) 48 см2.
1.10. Два кути трикутника дорівнюють 30о і 45о. Знайдіть його сторону,
протилежну куту 30о, якщо сторона, протилежна куту 45о, дорівнює
![]() см.
см.
А) 3 см; Б) 2 см; В) 2![]() см; Г) 2
см; Г) 2![]() см.
см.
1.11. Яка градусна міра кута правильного п’ятнадцятикутника?
А) 128о; Б) 144о; В) 150о; Г) 156о.
1.12. Точка А1(−1;4) є образом точки А(2; −8) при гомотетії з центром у
початку координат. Чому дорівнює коефіцієнт гомотетії?
А) 2; Б) −2; В) ![]() ; Г) −
; Г) − ![]() .
.
Частина друга
Розв’яжіть завдання 2.1 – 2.6. запишіть відповідь у бланк відповідей.
2.1. Спростіть вираз (2![]() − 5
− 5![]() +
+ ![]() )
)![]() −
− ![]() .
.
2.2. Учень 9 класу отримав за письмові роботи з алгебри оцінки 7,8, 7, 9,6.
Яку оцінку він має отримати за наступну роботу, щоб середній бал за всі роботи дорівнював 8?
2.3. Скільки цілих розв’язків має система нерівностей
![]()
2.4. Розв’яжіть рівняння ![]() +
+![]() =
= ![]() .
.
2.5. З точки до прямої проведено дві похилі, довжини яких дорівнюють 15см
і 20см. Знайдіть відстань від даної точки до прямої, якщо різниця проекцій похилих на цю пряму дорівнює 7см.
2.6. Складіть рівняння прямої, яка проходить через точки А(−1; 4) і В(−3; −2).
Частина третя
Розв’язання задач 3.1-3.4 повинно мати обґрунтування. У ньому потрібно записати послідовні логічні дії та пояснення, зробити посилення на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв’язання схемами, графіками, таблицями.
3.1. Побудуйте графік функції у= − х2 – 6х – 8. Користуючись побудованим
графіком, знайдіть:
1)область значень функції;
2)проміжок зростання функції.
3.2. У першому бідоні було молоко з масовою часткою жиру 2%, а в другому
- 5% . Скільки треба взяти молока з кожного бідона, щоб отримати 12кг молока, масова частка жиру якого дорівнює 4%?
3.3. При якому значенні х значення виразів 3х – 2, х+2 і х+8 будуть
послідовними членами геометричної прогресії ? Знайдіть члени цієї
прогресії.
3.4. Площа трикутника АВС дорівнює 18см2. На стороні АВ позначили точки
К і D так, що АК = КD = DВ, а на стороні АС – точки F і Е так, що АF =
FE = EC. Знайдіть площу чотирикутника DEFK .
Варіант 2
Частина перша
Завдання 1.1-1.12 мають по чотири варіанти відповідей, з яких тільки одна відповідь правильна. Оберіть правильну, на вашу думку, відповідь та позначте її у бланку відповідей.
1.1. Спростіть вираз 8а – (4а + 1).
А) 4а + 1; Б) 12а + 1; В) 4а – 1; Г) 12а – 1.
1.2. Якому одночлену дорівнює вираз (![]() m4)3 ?
m4)3 ?
А) ![]() m7; Б)
m7; Б) ![]() m12; В)
m12; В) ![]() m7; Г)
m7; Г) ![]() m12.
m12.
1.3. Розв’яжіть нерівність 6х + 7 ≤ − 11.
А) х ≥ −3; Б) х ≥ 3; В) х ≤ − 3; Г) х ≤ 3.
1.4. Обчисліть значення виразу (2 − ![]() )(2+
)(2+![]() ) .
) .
А) − 1; Б) 7; В) 5; Г) 1.
1.5. Скоротіть дріб ![]() .
.
A) ![]() ; Б)
; Б) ![]() ; B)
; B) ![]() ; Г)
; Г) ![]()
1.6. Знайдіть корені рівняння 4х2 – 3х – 1=0 .
А) 1; − ![]() ; Б) −1;
; Б) −1; ![]() В) 2; −
В) 2; − ![]() Г) − 2;
Г) − 2; ![]() .
.
1.7. Через яку з даних точок проходить графік функції у= 4х2 – 3 ?
А) А(− 2; − 13); Б) В( − 2;− 19); В) С( − 2; 19); Г) D( − 2;13).
1.8. Чому дорівнює четвертий член геометричної прогресії, перший член якої
b1= − 3, а знаменник q = 2 ?
А) 24; Б) – 24; В) 18; Г) – 18.
1.9. Знайдіть катет прямокутного трикутника, якщо його гіпотенуза дорівнює
27см, а проекція шуканого катета на гіпотенузу – 3см.
А) 6 см; Б) 9 см; В) 18 см; Г) 81 см.
1.10. У трикутнику АВС бісектриси кутів А і С перетинаються в точці О.
Яка з наступних рівностей є правильною ?
А) ![]() АОС = 90о −
АОС = 90о − ![]() <В; В) <АОС = 90о +
<В; В) <АОС = 90о + ![]() <В;
<В;
Б) <АОС = 90о − <В; Г) <АОС = 90о + <В.
1.11. Укажіть рівняння кола, яке є образом кола х2 + у2 = 4 при паралельному
![]() перенесенні на вектор а(2; −3).
перенесенні на вектор а(2; −3).
А) (х − 2)2 +(у – 3)2 =4; В) (х +2)2 +(у +3)2 =4;
Б) (х + 2)2 + (у – 3)2 = 4; Г) (х – 2)2 + (у + 3)2=4.
1.12. Сума трьох сторін паралелограма дорівнює 24 см. Знайдіть сторони
паралелограма, якщо його периметр становить 30 см.
А) 6см; 9см; 6см; 9см; В) 7см; 8см; 7см; 8см;
Б) 6см; 8см; 6см; 8см; Г) визначити неможливо.
Частина друга
Розв’яжіть завдання 2.1 – 2.6. запишіть відповідь у бланк відповідей.
2.1. Скоротіть дріб ![]() .
.
![]() 2.2. Розв’яжіть систему нерівностей
2.2. Розв’яжіть систему нерівностей ![]() –
– ![]() < −4,
< −4,
5х – 3 > 7х +21.
2.3. Знайдіть перший член арифметичної прогресії, різниця якої дорівнює 4, а
сума перших п’ятдесяти членів дорівнює 5500.
2.4. Розв’яжіть рівняння ![]() +
+ ![]() =
=![]() .
.
2.5. Знайдіть площу круга, вписаного в трикутник зі сторонами 13см, 14см і
15см.
2.6. У трикутнику АВС висота ВD поділяє сторону АС на відрізки АD і DC,
<А=45о, АВ = 6![]() см, DC =
см, DC =![]() см. Знайдіть сторону ВС трикутника.
см. Знайдіть сторону ВС трикутника.
Частина третя
Розв’язання задач 3.1-3.4 повинно мати обґрунтування. У ньому потрібно записати послідовні логічні дії та пояснення, зробити посилення на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв’язання схемами, графіками, таблицями.
3.1. Не виконуючи побудови, знайдіть координати точок перетину графіків
функцій у = х+3 і у = ![]() . Накресліть графіки даних функцій і позначте
. Накресліть графіки даних функцій і позначте
знайдені точки.
3.2. З одного поля зібрали по 40 ц ячменю з гектара, а з другого – по 35 ц з
гектара. Усього було зібрано 2600 ц. Наступного року урожайність першого поля збільшилась на 10%, другого – на 20%, а весь зібраний урожай збільшився на 400 ц. Знайдіть площу кожного поля.
3.3. Доведіть, що функція ![]() зростає на проміжку (2;+
зростає на проміжку (2;+ ![]() .
.
3.4. Більша діагональ прямокутної трапеції ділить її гострий кут навпіл, а
другу діагональ поділяє у відношенні 5:8, рахуючи від вершини тупого
кута. Знайдіть периметр трапеції, якщо її менша бічна сторона дорівнює
16 см.
Варіант 3
Частина перша
Завдання 1.1-1.12 мають по чотири варіанти відповідей, з яких тільки одна відповідь правильна. Оберіть правильну, на вашу думку, відповідь та позначте її у бланку відповідей.
1.1.Спростіть вираз (4а −1) + (1 − 2а) .
А) 6а; Б) 2а; В) 6а – 2; Г) 2а – 2.
1.2. Скоротіть дріб ![]()
A) 4m; Б) − 4m; B) ![]() ; Г) −
; Г) − ![]() .
.
1.3. Якому одночлену дорівнює вираз − 0,4a4 b2 ![]() 2 b3 ?
2 b3 ?
А) −4а6 b5; Б) – 40 а8 b6; В) − 4 а8 b6; Г) – 40 а6 b5.
1.4. Розв’яжіть нерівність 6х – 4 > 7х.
А) х > 4; Б) х > − 4; В) х < 4; Г) х < − 4.
1.5. Знайдіть за правилом підрахунку цифр суму наближених значень
х = 2,616 і у = 4,72.
А) 7,336; Б) 7,33; В) 7,34; Г) 7,3.
1.6. Обчисліть значення виразу ![]() при а = 3
при а = 3![]() .
.
А) 2; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
1.7. Вкажіть серед наведених послідовностей геометричну прогресію.
А) 4; 8; 12; 16; Б) 10; 20; 30; 40; В) 5;6;8; 11; Г) 7; 14;28;56.
1.8. Спростіть вираз ![]() –
– ![]() .
.
A) ![]() ; Б )
; Б ) ![]() ; B)
; B) ![]() ; Г )
; Г ) ![]() .
.
1.9. У трикутнику АВС відомо, що <С = 90о, ВС = 5см, АВ = 10см. Знайдіть
кут А цього трикутника.
А) 90о; Б) 60о; В) 45о; Г) 30о.
1.10. Скільки осей симетрії має прямокутник, який не є квадратом ?
А) жодної; Б) одну; В) дві; Г) чотири.
1.11. Чому дорівнює синус кута, якщо його косинус дорівнює 1 ?
А) 1; Б) – 1; В) −1 або 1; Г) 0.
1.12. Радіус вписаного кола правильного шестикутника дорівнює 4![]() см.
см.
Чому дорівнює радіус описаного кола цього шестикутника ?
А) 6см; Б) 8см; В) ![]() см; Г) 8
см; Г) 8![]() см.
см.
Частина друга
Розв’яжіть завдання 2.1 – 2.6. запишіть відповідь у бланк відповідей.
2.1. Розв’яжіть нерівність ![]() –
– ![]() ≤
≤![]() .
.
2.2. Чому дорівнює знаменник нескінченної геометричної прогресії,
перший член якої дорівнює 15, а сума дорівнює 75 ?
2.3. Розв’яжіть систему рівнянь ![]()
2.4. Було 300 г 5-відсоткового розчину солі. Через деякий час 50 г води
випарували. Яким став відсотковий вміст солі в розчині ?
2.5. Кути при основі одного рівнобедреного трикутника дорівнюють кутам
при основі другого рівнобедреного трикутника. Бічна сторона і основа
першого трикутника дорівнюють відповідно 15см і 18см, а висота другого
трикутника, проведена до основи – 24см. Чому дорівнює периметр
другого трикутника ?
2.6. Через точку М до кола з центром О проведено дотичні МА і МВ (А і В –
точки дотику). Знайдіть відстань від точки М до точок дотику, якщо
відстань між точками дотику дорівнює m і <АОВ = ![]() .
.
Частина третя
Розв’язання задач 3.1-3.4 повинно мати обґрунтування. У ньому потрібно записати послідовні логічні дії та пояснення, зробити посилення на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв’язання схемами, графіками, таблицями.
3.1. Побудуйте графік функції у = х2 – 4х – 5. Користуючись графіком,
знайдіть:
- множину розв’язків нерівності х2 – 4х – 5 ≤ 0;
- проміжок зростання функції.
3.2. Один з робітників може виконати виробниче завдання на 3 год швидше,
ніж другий . Якщо перший робітник буде працювати 4 год, а потім його
змінить другий, то останньому треба буде працювати 3 год, щоб
закінчити завдання. За скільки годин може виконати все завдання
перший робітник ?
3.3. Чому дорівнює сума всіх натуральних чисел, менших від 200, які
кратні 7 ?
3.4. Два кола мають зовнішній дотик у точці А, точки В і С – точки дотику
до цих кіл їх спільної дотичної. Доведіть, що кут ВАС – прямий.
Варіант 4
Частина перша
Завдання 1.1-1.12 мають по чотири варіанти відповідей, з яких тільки одна відповідь правильна. Оберіть правильну, на вашу думку, відповідь та позначте її у бланку відповідей.
- Спростіть вираз (5b – 2) + (2 – 2b).
- 3b − 4; Б) 7b – 4; B) 3b; Г ) 7b.
1.2. Скоротіть дріб ![]() .
.
A) − ![]() ; Б )
; Б ) ![]() ; B) − 5n; Г) 5n.
; B) − 5n; Г) 5n.
1.3. Якому одночлену дорівнює вираз − 0,6х3у∙100х2 у4 ?
А) – 60 х6 у4; Б) – 6 х6 у4; В) – 60 х5 у5; Г) – 6 х5 у5.
1.4. Розв’яжіть нерівність 4х – 7 > 5х .
А) х > − 7; Б) х < − 7; В) х > 7; Г) х < 7.
1.5. Знайдіть за правилом підрахунку цифр суму наближених значень
х = 3,528 і у = 6,43.
А) 9,958; Б) 9,9; В) 9,95; Г) 9,96.
1.6. Обчисліть значення виразу ![]() при b = 2
при b = 2![]() .
.
А) ![]() ; Б) 5; В)
; Б) 5; В) ![]() ; Г)
; Г) ![]() .
.
1.7. Вкажіть серед наведених послідовностей геометричну прогресію.
А)3;8;13;18; Б) 1;2;3;5; В) 6;18;54;162; Г)21;19;17;15.
1.8. Спростіть вираз ![]() –
– ![]() .
.
A) ![]() ; Б)
; Б) ![]() ; B)
; B) ![]() ; Г )
; Г ) ![]() .
.
1.9. Обчисліть площу рівнобедреного трикутника, бічна сторона якого
дорівнює 13см, а основа – 10см.
А) 130 см2; Б) 65 см2; В) 60 см2; Г) 120 см2.
1.10. Яка величина кута між бісектрисами двох суміжних кутів ?
А) 60о; Б) 90о; В) 120о; Г)залежить від величини кутів.
1.11. Який чотирикутник буде отримано, якщо сполучити кінці двох
перпендикулярних діаметрів кола ?
А) трапеція; Б) квадрат; В) ромб; Г) прямокутник.
1.12 .У певний момент часу довжина тіні дзвіниці Софіївського собору
дорівнює 19 м, а довжина тіні ліхтарного стовпа, який стоїть біля дзвіниці, - 1,5 м. Яка висота дзвіниці, якщо висота стовпа дорівнює 6 м ?
А) 76 м; Б) 72 м; В) 75 м; Г) 80 м.
Частина друга
Розв’яжіть завдання 2.1 – 2.6. запишіть відповідь у бланк відповідей.
2.1.Знайдіть добуток (2,6∙103)∙(4,5∙10−8) і запишіть результат у стандартному
вигляді.
2.2. Скільки цілих чисел містить множина розв’язків нерівності:
− 6 ≤ ![]() ≤ 2 ?
≤ 2 ?
2.3. Розв’яжіть систему рівнянь ![]()
2.4. Чому дорівнює значення виразу 3х1х2 – х1 – х2, де х1 і х2 – корені
рівняння х2+12х +19 = 0 ?
2.5 . Середина бічної сторони рівнобедреного трикутника віддалена від
його основи на 9см. Знайдіть відстань від точки перетину медіан
трикутника до його основи.
2.6. Одна із сторін паралелограма дорівнює 10см, менша діагональ – 14см,
а гострий кут – 60о. Знайдіть периметр цього паралелограма.
Частина третя
Розв’язання задач 3.1-3.4 повинно мати обґрунтування. У ньому потрібно записати послідовні логічні дії та пояснення, зробити посилення на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв’язання схемами, графіками, таблицями.
3.1.Побудуйте в одній системі координат графіки функцій у = ![]() і у = 6 – х.
і у = 6 – х.
За допомогою графіків укажіть значення х, при яких значення функції
у = 6 – х більші за значення функції у = ![]() .
.
3.2. За 5 кг цукерок і 4 кг печива заплатили 310 грн. Скільки коштує 1 кг
цукерок і 1 кг печива, якщо 3 кг цукерок дорожчі за 2 кг печива на
76 грн.?
3.3. Знайти область визначення функції у = ![]() −
− ![]() .
.
3.4. Діагональ рівнобічної трапеції перпендикулярна до бічної сторони, а
основи дорівнюють 7см і 25 см. Знайдіть довжини відрізків, на які
діагональ ділить висоту трапеції, проведену з вершини тупого кута.
Варіант 5
Частина перша
Завдання 1.1-1.12 мають по чотири варіанти відповідей, з яких тільки одна відповідь правильна. Оберіть правильну, на вашу думку, відповідь та позначте її у бланку відповідей.
1.1. Обчисліть значення виразу ![]() .
.
А) 4; Б) 3; В) 2; Г) 9.
1.2. Скоротіть дріб ![]() .
.
A) ![]() ; Б)
; Б) ![]() ; B)
; B) ![]() ; Г )
; Г ) ![]() .
.
1.3 Відомо, що а>0, с<0. Порівняйте з нулем значення виразу а3с6.
А) а3с6 < 0; Б) а3с 6> 0; В) а3с6 ≤ 0; Г) а3с6= 0.
1.4. Чому дорівнюють корені рівняння х2 − 13х+ 12 = 0 ?
А) – 1; 12; Б) – 1; − 12; В) 1; 12; Г) 1; −12.
1.5 Перший член арифметичної прогресії а1= 14, а різниця d = 0,5. Чому
дорівнює дев’ятий член прогресії?
А) 18; Б) 16,5; В) 16; Г) 18,5.
1.6. Виконайте ділення: ![]() : 17а8с2.
: 17а8с2.
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
1.7.Знайдіть розв’язок системи рівнянь ![]()
А) (3;4); Б) (4;3); В) (2;5); Г) (5; 2).
1.8. У книжці 130 сторінок. Тарас прочитав 104 сторінки. Скільки відсотків
книжки прочитав Тарас?
А) 60%; Б) 70%; В) 80%; Г) 90%.
1.9. Сума кутів опуклого многокутника дорівнює 1800о. Чому дорівнює
кількість його сторін?
А) 8; Б) 10; В) 12; Г) такий многокутник не існує.
1.10.Знайдіть площу круга, якщо довжина кола, яке його обмежує,
дорівнює 8π см.
А) 8π см2; Б) 16π см2; В) 32π см2; Г) 64π см2.
1.11.У трикутнику АВС відомо, що <В = 90о, АВ = 6см, ВС = 8см. Чому
дорівнює sinА ?
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
1.12.Обчисліть площу паралелограма, дві сторони якого дорівнюють 6см і
5![]() см, а кут між ними – 45о.
см, а кут між ними – 45о.
А) 30 см2; Б) 15 см2; В) 30![]() см2; Г) 15
см2; Г) 15![]() см2.
см2.
Частина друга
Розв’яжіть завдання 2.1 – 2.6. запишіть відповідь у бланк відповідей.
2.1. Знайдіть значення виразу ![]() ∙81
∙81![]() при а =
при а = ![]() , b =
, b = ![]() .
.
2.2. Спростіть вираз ![]() ∙
∙ ![]() +
+ ![]() .
.
2.3. Чому дорівнює сума семи перших членів геометричної прогресії
(bn), якщо b1=6, b6 =192 ?
2.4. Розв’яжіть рівняння ![]() –
– ![]() =
= ![]() .
.
2.5. Висота паралелограма, проведена з вершини тупого кута, дорівнює 6см і
ділить сторону паралелограма навпіл. Знайдіть меншу діагональ
паралелограма, якщо його гострий кут дорівнює 30о.
2.6. Діагональ BD чотирикутника ABCD є діаметром його описаного кола,
<ABD = 32o, <CBD =64о. Знайдіть кут між діагоналями чотирикутника,
який лежить проти сторони ВС.
Частина третя
Розв’язання задач 3.1-3.4 повинно мати обґрунтування. У ньому потрібно записати послідовні логічні дії та пояснення, зробити посилення на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв’язання схемами, графіками, таблицями.
3.1. Побудуйте графік функції у = − х2+ 6х – 8. Користуючись графіком,
знайдіть:
1) проміжок зростання функції;
2) при яких значеннях х функція набуває додатних значень.
3.2. Дві бригади мали прокласти по 720 м кабелю. Одна з них прокладала
щогодини на 2 м більше за другу і закінчила роботу на 18 год раніше від
неї. Скільки метрів кабелю прокладала щогодини кожна бригада?
![]() 3.3. Розв’яжіть систему рівнянь
3.3. Розв’яжіть систему рівнянь ![]() –
– ![]() = 1,
= 1,
х2 – 5ху +2у2 =32.
3.4. Бісектриса гострого кута паралелограма ділить його сторону у
відношенні 2:5, рахуючи від вершини тупого кута, який дорівнює 120о.
Обчисліть площу паралелограма, якщо його периметр дорівнює 54см.
Варіант 6
Частина перша
Завдання 1.1-1.12 мають по чотири варіанти відповідей, з яких тільки одна відповідь правильна. Оберіть правильну, на вашу думку, відповідь та позначте її у бланку відповідей.
1.1.Обчисліть значення виразу ![]() .
.
А) 16; Б) 8; В) 4; Г) 2.
1.2.Скоротіть дріб ![]() .
.
A) ![]() ; Б )
; Б ) ![]() ; B)
; B) ![]() ; Г)
; Г) ![]() .
.
1.3. Відомо, що m < 0, n < 0. Порівняйте з нулем значення виразу m5n6.
А) m5n6 = 0; Б) m5n6 > 0; В) m5n6 < 0; Г) m5n6 ≤ 0.
1.4. Чому дорівнюють корені рівняння х2 – 16х + 15 = 0 ?
А) − 1; − 15; Б) 1; − 15; В) – 1; 15; Г) 1;15.
1.5. Перший член арифметичної прогресії a1 = 8, а її різниця d = 0,4. Чому
дорівнює одинадцятий член прогресії?
А) 10,2; Б) 12; В) 12,8; Г) 14.
1.6. Виконайте ділення: ![]() : 19
: 19![]() .
.
A) ![]() ; Б )
; Б ) ![]() ; B)
; B)![]() ; Г)
; Г) ![]() .
.
1.7. Знайдіть розв’зок системи рівнянь ![]()
А) (2;6); Б) (6;2); В) (3;5); Г) (5;3).
1.8. У саду росте 180 фруктових дерев, з них 63 – вишні. Скільки відсотків
усіх дерев становлять вишні?
А) 36%; Б) 35%; В) 38%; Г) 37%.
![]()
![]() 1.9. При якому значенні n вектори
1.9. При якому значенні n вектори ![]() (n;3) і b( −3;3) перпендикулярні ?
(n;3) і b( −3;3) перпендикулярні ?
А) −3; Б) 3; В) – 2; Г) 2.
1.10. Укажіть правильне твердження:
А) будь – який правильний многокутник має центр симетрії;
Б) якщо сторони опуклого многокутника рівні, то він є правильним;
В) будь – який правильний многокутник має осі симетрії;
Г) якщо суми протилежних сторін опуклого чотирикутника рівні, то
навколо нього можна описати коло.
1.11. Знайдіть сторону квадрата, діагональ дорівнює 4 см.
А) 2![]() см; Б) 2 см; В)
см; Б) 2 см; В) ![]() см; Г) 4 см.
см; Г) 4 см.
1.12. Укажіть рівняння кола радіуса 4 з центром у точці В( − 2; 0).
А) (х – 2)2+ у2 = 4; В) (х− 2)2 + у2 = 16;
Б) (х+2)2+у2 = 16; Г) (х+ 2)2 + у2 = 4.
Частина друга
Розв’яжіть завдання 2.1 – 2.6. запишіть відповідь у бланк відповідей.
2.1. Якого найменшого значення може набувати вираз 4х2 – 16х+ 19 ?
2.2. Знайдіть корені рівняння (х2 + 5)(3х2 – 1) = 2х4 + 18х2.
2.3. Чому дорівнює сума шести перших членів геометричної прогресії
( bn), якщо b3 =12, b4 = − 24 ?
![]()
![]() 2.4. Спростіть вираз
2.4. Спростіть вираз ![]() +
+ ![]() :
: ![]() .
.
2.5. Точка дотику кола, вписаного в прямокутний трикутник, ділить один з
катетів на відрізки 2 см і 8 см, рахуючи від вершини прямого кута.
Знайдіть периметр трикутника.
2.6. Відрізок АМ – медіана трикутника з вершинами в точках А( −4; −2),
В(5; 3), С( − 3; −7). Складіть рівняння прямої АМ.
Частина третя
Розв’язання задач 3.1-3.4 повинно мати обґрунтування. У ньому потрібно записати послідовні логічні дії та пояснення, зробити посилення на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв’язання схемами, графіками, таблицями.
3.1. Не виконуючи побудови, знайдіть координати точок перетину графіків
функцій у = ![]() і у = 5 – х. Накресліть графіки даних функцій і позначте
і у = 5 – х. Накресліть графіки даних функцій і позначте
знайдені точки.
3.2. Катер проплив 40 км за течією річки і 36 км по озеру, витративши на
весь шлях 4 год. Знайдіть власну швидкість катера, якщо швидкість течії
річки становить 2 км/год.
3.3. Знайдіть область визначення функції у = ![]() +
+ ![]() .
.
3.4. Діагоналі трапеції ABCD з основами BC і AD перетинаються в точці О,
AO = OD. Доведіть, що дана трапеція рівнобічна.
Варіант 7
Частина перша
Завдання 1.1-1.12 мають по чотири варіанти відповідей, з яких тільки одна відповідь правильна. Оберіть правильну, на вашу думку, відповідь та позначте її у бланку відповідей.
1.1.Виконайте ділення: ![]() :
: ![]() .
.
А) х3; Б) х4; В) х2; Г) х.
1.2.Чому дорівнює шостий член геометричної прогресії, якщо її перший
член b1 = 96, а знаменник q = − ![]() ?
?
А) 2; Б) − 2; В) 3; Г) – 3.
1.3. Розв’яжіть нерівність 35х + 5 ≤ 0.
А) х ≤ 7; Б) х ≤ − 7; В) х ≤ ![]() ; Г) х ≤ −
; Г) х ≤ − ![]() .
.
1.4.Знайдіть корінь рівняння х(х+9) = (х+3)(х−3).
А) 1; Б) – 1; В) 3; Г) −3.
1.5. При яких значеннях змінної не має змісту вираз ![]() ?
?
А) 0;4; Б) 0; − 4; В) 0; Г) 4.
1.6. Розкладіть на множники многочлен 3а2 – 30а + 75.
А) 3(а – 5)(а+5); Б) 3(а−5)2; В) 3(а+5)2; Г) 3(а−5)2(а+5)2.
1.7. Скоротіть дріб ![]() .
.
A) b − 2; Б) b + 2; B)![]() +2; Г )
+2; Г ) ![]() − 2.
− 2.
1.8. Який відсотковий вміст солі в розчині, якщо 700 г розчину містить
112 г солі ?
А) 15%; Б) 18%; В) 17%; Г) 16 %.
1.9. Яку частину площі круга становить площа сектора, градусна міра дуги
якого дорівнює 72о?
![]()
![]() А)
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
1.10. Знайдіть координати суми векторів АВ і ВС, якщо А(2; 4), С(3; − 2), В –
деяка точка площини.
А) (5; 2); Б) (1; − 6); В) (2,5; 1); Г) знайти неможливо.
1.11. Як можна закінчити речення « У будь – якій рівнобічній трапеції…»,
щоб утворилося правильне твердження?
А) діагоналі перпендикулярні;
Б) діагоналі точкою перетину діляться навпіл;
В) діагоналі ділять кути трапеції навпіл;
Г) діагоналі рівні.
1.12. У трикутнику АВС відомо, що АВ = 12 см, sin B = 0,4, sin C = 0,12.
Знайдіть довжину сторони АС.
А) 4 см; Б) 40 см; В) 3,6 см; Г) 36 см.
Частина друга
Розв’яжіть завдання 2.1 – 2.6. запишіть відповідь у бланк відповідей.
2.1. Знайти нулі функції у = − 4х4+5х2 – 1.
![]() 2.2. Розв’яжіть систему нерівностей
2.2. Розв’яжіть систему нерівностей ![]() +
+![]() < 6,
< 6,
(х – 4)2 < (х+1)(х − 3) – 5.
2.3. Чому дорівнює сума двадцяти перших членів арифметичної прогресії
(аn), якщо а5 = − 0,8, а11 = − 5 ?
2.4. Число – 3 є коренем рівняння 2х2 + 3х+а = 0. Знайдіть другий корінь
рівняння і значення а.
2.5. Один з катетів прямокутного трикутника дорівнює 15 см , а медіана,
проведена до гіпотенузи, - 8,5 см. Обчисліть площу даного трикутника.
2.6. Радіус кола, описаного навколо трикутника АВС , дорівнює 6 см.
Знайдіть радіус кола, описаного навколо трикутника АОС, де О – точка
перетину бісектрис трикутника АВС, якщо <АВС = 60о.
Частина третя
Розв’язання задач 3.1-3.4 повинно мати обґрунтування. У ньому потрібно записати послідовні логічні дії та пояснення, зробити посилення на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв’язання схемами, графіками, таблицями.
3.1. Побудуйте графік функції у = х2+4х. Користуючись графіком, знайдіть:
1) проміжок спадання функції;
2) множину розв’язків нерівності х2+4х ≥ 0.
3.2. Набираючи щодня на 3 сторінки більше, ніж планувалося, оператор
комп’ютерного набору закінчив роботу обсягом 60 сторінок на день
раніше строку. Скільки сторінок набирав він щодня ?
3.3. Складіть квадратне рівняння, корені якого на 4 більші за відповідні
корені рівняння х2 – 2х − 4 = 0.
3.4. Точка дотику кола, вписаного в прямокутну трапецію, ділить її більшу
основу на відрізки завдовжки 20 см і 25 см. Обчисліть периметр
трапеції.
Варіант 8
Частина перша
Завдання 1.1-1.12 мають по чотири варіанти відповідей, з яких тільки одна відповідь правильна. Оберіть правильну, на вашу думку, відповідь та позначте її у бланку відповідей.
-
Виконайте ділення:
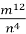 :
: 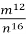 .
.
-
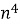 ; Б)
; Б) 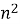 ; B)
; B) 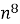 ; Г )
; Г ) 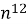 .
.
-
Чому дорівнює п’ятий член геометричної прогресії, якщо її перший член b1 = 405, а знаменник q = −
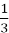 ?
?
-
Чому дорівнює п’ятий член геометричної прогресії, якщо її перший член b1 = 405, а знаменник q = −
А) – 5; Б) 5; В) – 3; Г) 3.
1.3. Розв’яжіть нерівність 18х + 3 ≥ 0
А) х ≥ ![]() ; Б) х ≥ 6; В) х ≥ −
; Б) х ≥ 6; В) х ≥ − ![]() ; Г) х ≥ − 6.
; Г) х ≥ − 6.
1.4 Знайдіть корінь рівняння х(х – 4) = (х+2)(х – 2).
А) − 1; Б) − 2; В) 1; Г) 2.
1.5. При яких значеннях змінної не має змісту вираз ![]() ?
?
А) 0;− 5; Б) 0; 5; В) 5; Г) 0.
1.6. Розкладіть на множники многочлен 2b2 + 24b + 72.
A) 2(b+6)2; Б) 2(b – 6)2; B) 2(b – 6)(b+6); Г) 2(b+6)2(b – 6)2.
1.7. Скоротіть дріб ![]() .
.
А) ![]() +3; Б)
+3; Б) ![]() − 3; В) а + 3; Г) а – 3.
− 3; В) а + 3; Г) а – 3.
1.8. Який відсотковий вміст заліза в руді, якщо 600 кг руди містять 54 кг
заліза?
А) 7%; Б) 8%; В) 9%; Г) 10%.
![]() 1.9. Дано точки М(4; −2) і К(2; 1). Знайдіть координати вектора МК.
1.9. Дано точки М(4; −2) і К(2; 1). Знайдіть координати вектора МК.
![]()
![]()
![]()
![]() А) МК (2; −3); Б) МК ( − 2; 3); В) МК (2; 3); Г) МК (− 2; − 3).
А) МК (2; −3); Б) МК ( − 2; 3); В) МК (2; 3); Г) МК (− 2; − 3).
1.10. Яку з наведених властивостей має будь – який ромб?
А) діагоналі рівні;
Б) діагоналі перпендикулярні;
В) один з кутів дорівнює 60о;
Г) кут між діагоналями дорівнює 60о.
1.11. Чому дорівнює площа паралелограма, сторони якого дорівнюють 8 см і
10 см, а кут між ними – 60о ?
А) 80 см2; Б) 40 см2; В) 80![]() см2; Г) 40
см2; Г) 40![]() см2.
см2.
1.12. Які координати має образ точки В(3; − 4) при симетрії відносно осі
абсцис?
А) ( −4; 3); Б)(3; 4); В) (− 3; − 4); Г)( − 3; 4).
Частина друга
Розв’яжіть завдання 2.1 – 2.6. запишіть відповідь у бланк відповідей
2.1. У саду росли яблуні і вишні, причому яблуні становили 52% усіх дерев.
Вишень було на 8 дерев менше, ніж яблунь. Скільки дерев росло в саду?
2.2. Розв’яжіть систему нерівностей ![]()
2.3. Знайдіть значення виразу а2 − 2![]() а + 1 при а =
а + 1 при а = ![]() +4.
+4.
2.4. Перетворіть вираз ![]() −3 :
−3 : ![]() −2 так, щоб він не містив степенів
−2 так, щоб він не містив степенів
з від’ємними показниками.
2.5. Знайдіть градусну міру дуги кола, довжина якої дорівнює π см, якщо
радіус кола дорівнює 12 см.
2.6. Продовження бічних сторін АВ і CD трапеції ABCD перетинаються
в точці Е. Знайдіть ED, якщо CD = 8 см, BC :AD = 3:5.
Частина третя
Розв’язання задач 3.1-3.4 повинно мати обґрунтування. У ньому потрібно записати послідовні логічні дії та пояснення, зробити посилення на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв’язання схемами, графіками, таблицями.
3.1. Не виконуючи побудови, знайдіть координати точок перетину графіків
функцій у = 5 – х2 і у = х−1. Накресліть графіки даних функцій і позначте
знайдені точки.
3.2. Одному робітникові для виконання виробничого завдання потрібно
на 2 год більше, ніж другому. Перший робітник пропрацював 2 год, а
потім його змінив другий. Після того як другий робітник пропрацював
3 год, виявилось, що виконано ![]() завдання. За скільки годин може
завдання. За скільки годин може
виконати це завдання кожний робітник, працюючи самостійно ?
3.3. Знайдіть область визначення функції у = ![]() +
+ ![]() .
.
3.4. У прямокутну трапецію вписано коло. Точка дотику ділить більшу з
бічних сторін трапеції на відрізки 4 см і 25 см. Знайдіть площу трапеції.
Варіант 9
Частина перша
Завдання 1.1-1.12 мають по чотири варіанти відповідей, з яких тільки одна відповідь правильна. Оберіть правильну, на вашу думку, відповідь та позначте її у бланку відповідей.
- Обчисліть значення виразу (64)3: 610.
А) 6; Б) 36; В) 216; Г) 1.
1.2. Розкладіть на множники вираз a2 b – ab2.
A) a2 b2(a−b); Б) ab(a−b); B) a(a−b); Г) b(a − b).
1.3. Спростіть вираз х(х −8) – (х2 + 2х).
А) 10х; Б) 6х; В) − 10х; Г) – 6х.
1.4. Чому дорівнює різниця арифметичної прогресії (аn), якщо а1= −6; а2 =− 4?
А) −10; Б) −2; В) 10; Г) 2.
1.5. Яка з функцій є лінійною?
А) у = ![]() +1; Б) у =
+1; Б) у = ![]() + 1; В) у = х3+1; Г) у =
+ 1; В) у = х3+1; Г) у = ![]() +1.
+1.
1.6. Порівняйте числа а і b, якщо a - b = − 4,6.
А) a > b; Б) a < b ; В) a = b; Г) a ≥ b.
1.7. Скоротіть дріб ![]() .
.
A) m − 5; Б) m + 5; B) m − ![]() ; Г ) m +
; Г ) m + ![]() .
.
1.8. Площа поля становить 350 га. Пшеницею засіяли 18% поля. Скільки
гектарів засіяли пшеницею?
А) 60 га; Б) 68 га; В) 63 га; Г) 72 га.
1.9. У колі, радіус якого дорівнює 20 см, проведено хорду на відстані 12 см
від його центра. Чому дорівнює довжина цієї хорди?
А) 16 см; Б) 32 см; В) 8 см; Г) 48см.
1.10. Яка з даних фігур має центр симетрії?
А) трикутник; Б) трапеція; В) відрізок; Г) кут.
1.11. У трикутнику АВС відомо, що АВ = 12 см, ВС = 16 см, АС = 20 см,
точка D ― середина АВ, точка Е – середина сторони АС. Знайдіть
периметр чотирикутника BDEC.
А) 80 см; Б) 48 см; В) 24 см; Г) 40см.
1.12. Сторона прямокутника дорівнює 12 см і утворює з його діагоналлю
кут 30о. Знайдіть другу сторону прямокутника.
А) 6 см; Б) 6![]() см; В) 4
см; В) 4![]() см; Г) 12
см; Г) 12![]() см.
см.
Частина друга
Розв’яжіть завдання 2.1 – 2.6. запишіть відповідь у бланк відповідей.
2.1. Чому дорівнює перший від’ємний член арифметичної прогресії
6,8; 6; 5,2;….?
2.2. Розв’яжіть систему рівнянь ![]()
2.3. Знайдіть множину розв’язків нерівності (х – 1)(х – 3) ≤ 27 – 2х.
2.4. Спростіть вираз ![]() :
: ![]() .
.
2.5. Пряма, паралельна стороні АС трикутника АВС, перетинає його сторону
АВ у точці М, а сторону ВС – у точці К. Знайдіть площу трикутника
АВС, якщо ВМ = 3 см, АМ = 4 см, а площа чотирикутника АМКС
дорівнює 80 см2.
2.6. Висота рівнобедреного тупокутного трикутника, проведена до його
основи, дорівнює 8 см, а радіус описаного навколо нього кола – 13 см.
Знайдіть бічну сторону трикутника.
Частина третя
Розв’язання задач 3.1-3.4 повинно мати обґрунтування. У ньому потрібно записати послідовні логічні дії та пояснення, зробити посилення на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв’язання схемами, графіками, таблицями.
3.1. Корені х1 і х2 рівняння х2 – 6х+ с = 0 задовольняють умову х1+4х2 = 18.
Знайдіть корені рівняння і значення с.
3.2. На шлях, що дорівнює 18 км, велосипедист витратив на 1год 48 хв
менше, ніж пішохід, оскільки за 1 год проїжджав на 9 км більше, ніж
проходив пішохід. Знайдіть швидкості велосипедиста й пішохода.
![]() 3.3. Побудуйте графік функції
3.3. Побудуйте графік функції ![]() , якщо х < − 2,
, якщо х < − 2,
у = − 2х, якщо −2 ≤ х ≤ 2,
![]() , якщо х > 2.
, якщо х > 2.
Користуючись побудованим графіком, знайдіть проміжки зростання і
проміжки спадання функції.
3.4. Сторони трикутника дорівнюють 6 см і 8 см. Медіана трикутника,
проведена до його третьої сторони, дорівнює ![]() см. Знайдіть невідому
см. Знайдіть невідому
сторону трикутника.
Варіант 10
Частина перша
Завдання 1.1-1.12 мають по чотири варіанти відповідей, з яких тільки одна відповідь правильна. Оберіть правильну, на вашу думку, відповідь та позначте її у бланку відповідей.
- Обчисліть значення виразу (43)5 : 412.
А) 1; Б) 4; В) 16; Г) 64.
1.2. Розкладіть на множники вираз m2n+ mn2.
A) m(m+n); Б) n(m+n); B) mn(m+n); Г) m2n2(m+n).
1.3. Спростіть вираз (х2 – 3х) – х(х+4).
А) 7х; Б) – 7х; В) − х; Г) х.
1.4. Чому дорівнює різниця арифметичної прогресії (аn), якщо а1 = − 2;
а2 = 3 ?
А) −1; Б) 1; В) – 5; Г) 5.
1.5. Яка з функцій є лінійною?
А) у = ![]() − 4; Б) у = х2 – 4; В) у =
− 4; Б) у = х2 – 4; В) у = ![]() − 4; Г) у = х3 − 4.
− 4; Г) у = х3 − 4.
1.6. Порівняйте числа а і b, якщо а –b = 3,4.
А) a ≤ b; Б) a < b; В) a > b; Г) a = b.
1.7. Скоротіть дріб ![]() .
.
А) а – 7; Б) а + 7; В) а −![]() ; Г) а +
; Г) а + ![]() .
.
1.8. Сплав містить 5% міді. Скільки кілограмів міді міститься в 420 кг
сплаву ?
А) 20 кг; Б) 21 кг; В) 22 кг; Г) 24 кг.
1.9. Дано рівняння кола (х+4)2 + (у – 15)2 = 20. Чому дорівнює радіус кола?
А)![]() ; Б)
; Б) ![]() ; В) 20; Г) 10.
; В) 20; Г) 10.
1.10. Кути трапеції ABCD, прилеглі до основи ВС, дорівнюють 70о і 160о.
Знайдіть кути, прилеглі до основи AD.
А) 20о і 110о; Б) 40о і 130о; В) 50о і 120о; Г) такої трапеції не існує.
1.11. Чому дорівнює радіус кола, вписаного в правильний трикутник зі
стороною 18 см?
А) 18![]() см; Б) 9
см; Б) 9![]() см; В) 6
см; В) 6![]() см; Г) 3
см; Г) 3![]() см.
см.
1.12. Чому дорівнює менша із сторін паралелограма, якщо одна з них на 5см
більша за другу, а периметр паралелограма дорівнює 70 см?
А) 10 см; Б) 15 см; В) 20 см; Г) 25 см.
Частина друга
Розв’яжіть завдання 2.1 – 2.6. запишіть відповідь у бланк відповідей.
2.1. Чому дорівнює значення виразу (2![]() − 7
− 7![]() −
− ![]() )∙ 2
)∙ 2![]() ?
?
2.2. Розв’яжіть нерівність 2 < ![]() ≤ 5.
≤ 5.
2.3. Знайдіть суму нескінченної геометричної прогресії (bn), якщо b1 = − 90,
b4 = ![]() .
.
2.4. Спростіть вираз ![]() :
: ![]() .
.
2.5. Діагоналі трапеції ABCD (AD ![]() BC) перетинаються в точці О,
BC) перетинаються в точці О,
BO: OD = 3:4, BC =18 см. Знайдіть основу AD трапеції.
2.6. Висота ВМ трикутника АВС ділить сторону АС на відрізки АМ і МС,
МС = 4![]() см, АВ = 4 см, <А = 45о. Знайдіть площу трикутника АВС.
см, АВ = 4 см, <А = 45о. Знайдіть площу трикутника АВС.
Частина третя
Розв’язання задач 3.1-3.4 повинно мати обґрунтування. У ньому потрібно записати послідовні логічні дії та пояснення, зробити посилення на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв’язання схемами, графіками, таблицями.
3.1. Побудуйте графік функції у = 8 −2х – х2. Користуючись графіком,
знайдіть:
- область значень даної функції;
- при яких значеннях х функція набуває від’ємних значень.
3.2. Маємо два сплави міді й цинку. Перший сплав містить 9% , а другий –
30% цинку. Скільки треба взяти кілограмів першого сплаву і скільки
кілограмів другого, щоб отримати сплав масою 300 кг, що містить 23%
цинку ?
3.3. Знайдіть суму всіх натуральних чисел, які кратні 6 і менші від 250.
3.4. Центр кола, вписаного в рівнобедрений трикутник, ділить його висоту,
проведену до основи, на відрізки, довжини яких дорівнюють 10 см і
26 см. Знайдіть площу даного трикутника.
Відповіді до атестаційних робіт
Варіант 1
Частина перша
номер задачі
|
варіант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
1 |
Б |
В |
Б |
Г |
В |
А |
В |
Г |
В |
А |
Г |
Г |
Частина друга
2.1. – 18 2.4. 1
2.2. 11 балів 2.5. 12 см
2.3. 2 2.6. у = 3х+7.
Частина третя
3.1. 1. (−![]() ; 1] – область значень; 2. (−
; 1] – область значень; 2. (−![]() ; − 3].
; − 3].
3.2. 4 кг; 8 кг.
3.3. −10; −32;−8;−2; 1; 1; 3; 9.
3.4. 6 см2.
![]()
Частина перша
Номер задачі
|
варіант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
2 |
В |
Б |
В |
Г |
Б |
А |
Г |
Б |
Б |
В |
Г |
А |
Частина друга
2.1. ![]() 2.4. 0,5
2.4. 0,5
2.2. (−![]() ; − 12) 2.5. 16
; − 12) 2.5. 16![]() см2
см2
2.3. 12 2.6. 7 см.
Частина третя
З.1. (−4; − 1); (1; 4)
3.2. 30 га; 40 га.
3.3. функція зростає на (2;+ ![]() ).
).
3.4. 88 см.
Частина перша
Номер задачі
|
варіант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
3 |
Б |
А |
Г |
Г |
В |
А |
Г |
Б |
Г |
В |
Г |
Б |
Частина друга
2.1. [−5; +![]() ) 2.4. 6%
) 2.4. 6%
2.2. 0,8 2.5. 96 см
2.3. (1; − 1), (0,6; − 2,2). 2.6. ![]() .
.
Частина третя
3.1. ![]() , 2. [2; +
, 2. [2; +![]() ).
).
3.2. 6 год
3.3. 2842
3.4. <ВАС = 90о, що й треба було довести.
![]()
Частина перша
Номер задачі
|
варіант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
4 |
В |
Г |
В |
Б |
Г |
Б |
В |
Г |
В |
Б |
Г |
А |
Частина друга
2.1. 1,17∙ 10−4 2.4. 69
2.2. 7 2.5. 6 см
2.3. (6;2), (2; − 2) 2.6. 52 см
Частина третя
3.1. Значення функції у = 6 – х більші від значень функції у = ![]() , якщо
, якщо
х![]() [0; 4)
[0; 4)
3.2. 42 грн., 25 грн.
3.3. (−![]()
3.4. 5,25 см; 6,75 см.
Частина перша
Номер задачі
|
варіант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
5 |
В |
Г |
Б |
В |
А |
Г |
Б |
В |
В |
Б |
В |
А |
Частина друга
2.1. 6 2.4. 2
2.2. ![]()
![]() 2.5. 12 см
2.5. 12 см
2.3. 762 2.6. 58о
Частина третя
3.1. 1. (−![]()
3.2. 10 м; 8 м.
3.3. (−2;2); (2; − 2)
3.4. 63![]() см2
см2
![]()
Частина перша
Номер задачі
|
варіант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
6 |
Г |
Б |
В |
Г |
Б |
В |
Г |
Б |
Б |
В |
А |
Б |
Частина друга
2.1. 3 2.4. ![]()
2.2. ![]() ; −
; − ![]() . 2.5. 26
. 2.5. 26![]() см
см
2.3. – 63 2.6. у = − 2
Частина третя
3.1 (2;3); (3;2)
3.2. 18 км/год
3.3. [−1; 5)
3.4. АВСД – трапеція рівнобічна
Частина перша
Номер задачі
|
варіант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
7 |
Б |
Г |
Г |
Б |
Г |
Б |
В |
Г |
В |
Б |
Г |
Б |
Частина друга
2.1. −1; − ![]() ;
; ![]() ; 1. 2.4. х2 = 1,5; а = − 9
; 1. 2.4. х2 = 1,5; а = − 9
2.2. (4;16) 2.5. 60 см2
2.3. – 93 2.6. 6 см.
Частина третя
3.1 ![]() 2. (−
2. (− ![]() )
)
3.2. 15 сторінок
3.3 х2 – 10х + 20 = 0
3.4. 162 см
![]()
Частина перша
Номер задачі
|
варіант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
8 |
Г |
Б |
В |
В |
В |
А |
Б |
В |
Б |
Б |
Г |
Б |
Частина друга
2.1 200 дерев 2.4. ![]()
2 .2. [0,8; 1] 2.5. 15о
2.3. 12 2.6. 20 см
Частина третя
3.1. А(−3;−4); В(2;1)
3.2. 8 год; 6год.
3.3. [−6; 2)
3.4. 490 см2
Частина перша
Номер задачі
|
варіант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
9 |
Б |
Б |
В |
Г |
А |
Б |
Г |
В |
Б |
В |
Г |
В |
Частина друга
2.1. −0,4 2.4. 1
2.2. (6; −1); (1,5; 3,5) 2.5. 98 см2
2.3. [−4; 6] 2.6. 4![]() см
см
Частина третя
3.1. 2; 4; 8.
3.2. 15км/год; 6 км/год.
3.3. Функція зростає на проміжку (-![]() спадає на
спадає на
проміжку [−2;2]
3.4. 4см.
![]()
Частина перша
Номер задачі
|
варіант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
10 |
Г |
В |
Б |
Г |
В |
В |
В |
Б |
А |
А |
Г |
Б |
Частина друга
2.1 −10 2.4. х+1
2.2. [−4; 0,5] 2.5. 24 см
2.3. – 54 2.6. 12 см2
Частина третя
3.1. 1. (−![]() ; 2. (−
; 2. (−![]()
3.2. 100кг; 200 кг.
3.3. 5166
3.4. 540см2

про публікацію авторської розробки
Додати розробку
