Квадратична функція і її графік покрокове детальна побудова графіка функції
Мета : розглянути побудову графіка функції y=ax2+bx+c та її властивості використовуючи графік функції y = ax2 навчитись знаходити значення функції, значення аргументу, розвивати вміння увагу й систематизувати вивчений матеріал; розвивати графічну грамотність.
Обладнання : Комп'ютери, програмне забезпечення Microsoft Office Power Point
- самостійна робота.doc doc
- уроку.doc doc
- функція.ppt ppt
- .doc doc
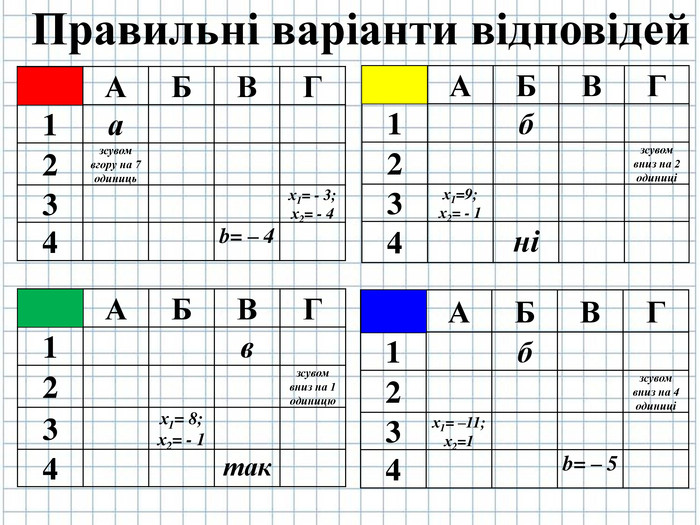
![]() I варіант
I варіант
Виберіть правильний варіант відповіді
-
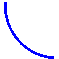
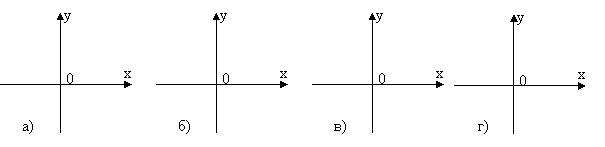 На якому з малюнків зображено графік функції у=
На якому з малюнків зображено графік функції у=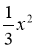 ?
?

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
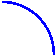
- Графік функції у=х2 +7 отримано з графіка функції у= х2:
а) зсувом вгору на 7 одиниць;
б) зсувом праворуч на 7 одиниць;
в) зсувом ліворуч на 7 одиниць;
г) зсувом вниз на 7 одиниць;
- Знайдіть корені квадратного тричлена х2+7х+12.
а) х1=6; х2=4;
б) х1= – 5; х2=7;
в) х1=3; х2= 4;
г) х1= – 3; х2= – 4.
- При яких значеннях b графік функції y=3x2+bx– 2 проходить через точку D(–1;5)?
а) b=4;
б) b=7;
в) b= – 4;
г) b= 5.
Учень 9 класу ______________________________________
( Прізвище, Ім’я )
|
|
А |
Б |
В |
Г |
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
4 |
|
|
|
|
![]()
II варіант
Виберіть правильний варіант відповіді
-
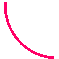
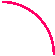
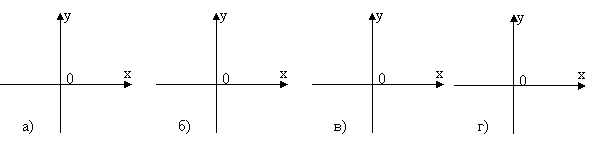 На якому з малюнків зображено графік функції у=
На якому з малюнків зображено графік функції у=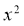 ?
?



![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
- Графік функції у=х2 – 2 отримано з графіка функції у= х2:
а) зсувом вгору на 2 одиниці;
б) зсувом праворуч на 2 одиниці;
в) зсувом ліворуч на 2 одиниці;
г) зсувом вниз на 2 одиниці.
- Знайдіть корені квадратного тричлена х2 – 8х – 9 .
а) х1=9; х2= – 1;
б) х1= – 5; х2=7;
в) х1=3; х2= - 9;
г) х1= – 3; х2= – 4.
- Чи проходить графік функції y=x2– 5x+6 через точку А(–3;14)?
а) можливо так, а можливо й ні;
б) ні;
в) так;
г) не можна сказати.
Учень 9 класу ______________________________________
( Прізвище, Ім’я )
|
|
А |
Б |
В |
Г |
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
4 |
|
|
|
|
![]()
ІІI варіант
Виберіть правильний варіант відповіді
-
На якому з малюнків зображено графік функції у=2
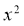 ?
?

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

- Графік функції у=3х2 – 1 отримано з графіка функції у= 3х2:
а) зсувом вгору на 1 одиницю;
б) зсувом праворуч на 1 одиницю;
в) зсувом ліворуч на 1 одиницю;
г) зсувом вниз на 1 одиницю.
- Знайдіть корені квадратного тричлена х2– 7х– 8.
а) х1=9; х2=1;
б) х1= 8; х2= - 1;
в) х1=3; х2= – 9;
г) х1= – 3; х2= – 4.
- Чи проходить графік функції y=x2– 7x+6 через точку В(–1;14)?
а) можливо так, а можливо й ні;
б) ні;
в) так;
г) не можна сказати.
Учень 9 класу ______________________________________
( Прізвище, Ім’я )
|
|
А |
Б |
В |
Г |
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
4 |
|
|
|
|
![]()
IV варіант
Виберіть правильний варіант відповіді
-

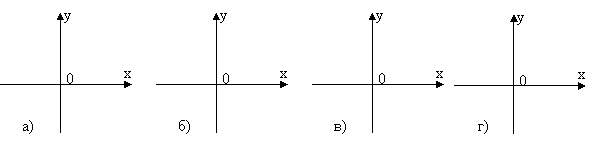
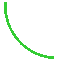
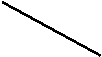
 На якому з малюнків зображено графік функції у=
На якому з малюнків зображено графік функції у=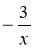 ?
?
![]()
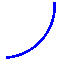
![]()
![]()
![]()
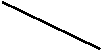
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
-
Графік функції у=
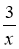 – 4 отримано з графіка функції у=
– 4 отримано з графіка функції у= 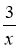 :
:
а) зсувом вгору на 4 одиниці;
б) зсувом праворуч на 4 одиниці;
в) зсувом ліворуч на 4 одиниці;
г) зсувом вниз на 4 одиниці.
- Знайдіть корені квадратного тричлена х2+10х– 11.
а) х1=–11; х2=1;
б) х1= – 5; х2=7;
в) х1=11; х2= – 1;
г) х1= – 3; х2= – 4.
- При яких значеннях b графік функції y=x2– bx– 2 проходить через точку С(1;4)?
а) b=4;
б) b=7;
в) b= – 5;
г) b= 5.
Учень 9 класу ______________________________________
( Прізвище, Ім’я )
|
|
А |
Б |
В |
Г |
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
4 |
|
|
|
|
Тема. Квадратична функція і її графік
Мета : розглянути побудову графіка функції y=ax2+bx+c та її властивості використовуючи графік функції y = ax2 навчитись знаходити значення функції, значення аргументу, розвивати вміння увагу й систематизувати вивчений матеріал; розвивати графічну грамотність.
Обладнання : Комп’ютери, програмне забезпечення Microsoft Office Power Point
ХІД УРОКУ
І. Організаційний момент
ІІ. Актуалізація опорних знань :
Самостійна робота на 5 – 7 хвилин з миттєвою перевіркою та оцінюванням.
Повідомлення учнів:
Історичні матеріали про вчених-математиків: Франсуа Вієта, Рене Декарта, Мухамеда аль Хорезмі
ІІІ. Вивчення нового матеріалу.
Узагальнення та систематизація знань і умінь набутих раніше.
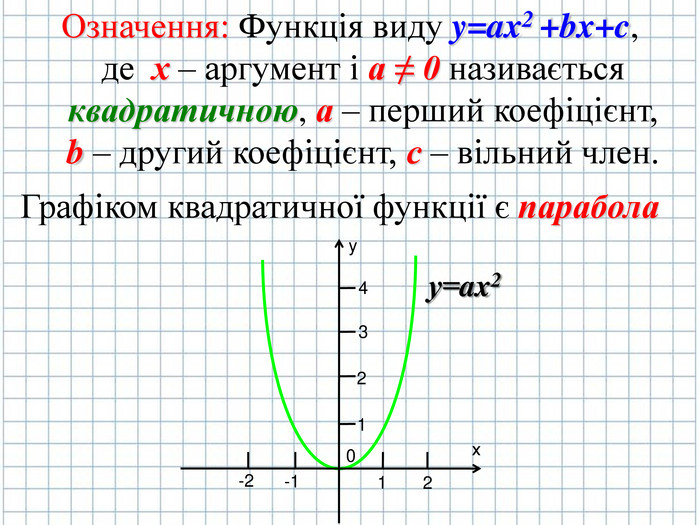
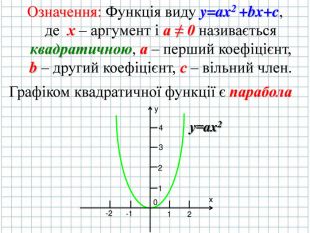
Розглянемо квадратичну функцію y = ax2 +bx + c дамо означення квадратичної функції
Функція виду y=ax2 +bx+c, де х – аргумент і а ≠ 0 називається квадратичною, а – перший коефіцієнт, b – другий коефіцієнт, с – вільний член (слайд № 4)
Застосування квадратичної функції надзвичайно широке – ми використовуємо квадратичну функцію під час розв’язування задач на знаходження невідомих в задачах на швидкість при розв’язку задач на знаходження площі під час розв’язування систем рівнянь методом підстановки та методом Гауса. (слайд № 3)
Завдання уроку
Для того щоб розглянути властивості та графік квадратичної функції сплануємо нашу роботу таким чином:
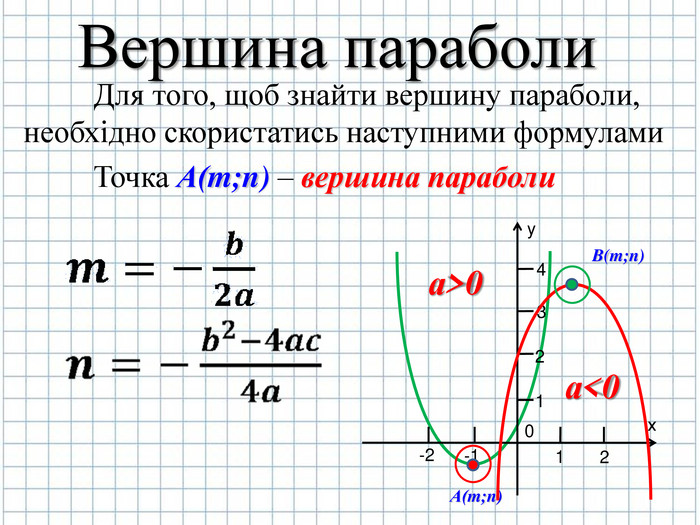
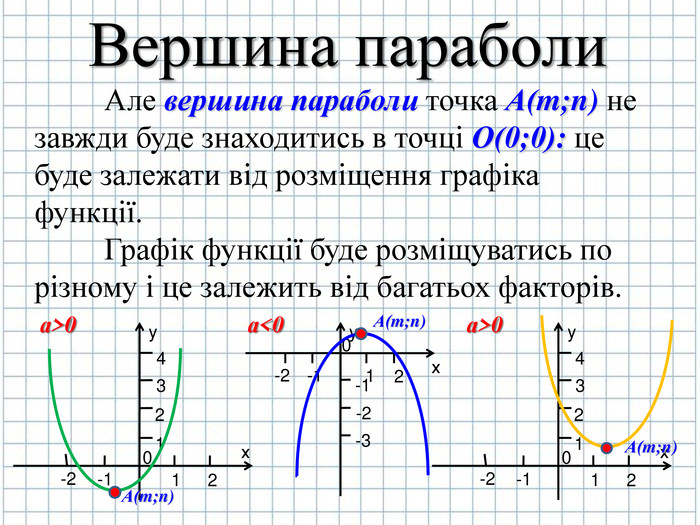
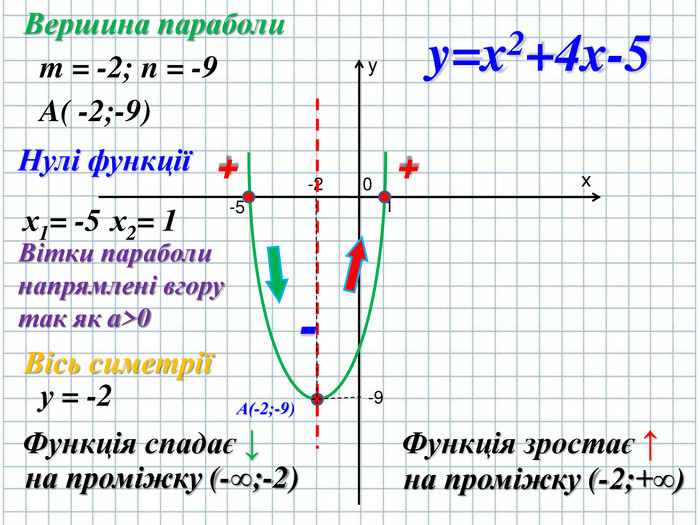
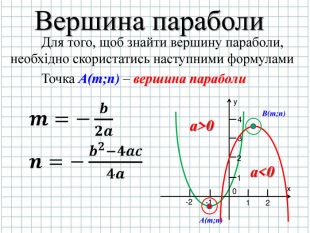
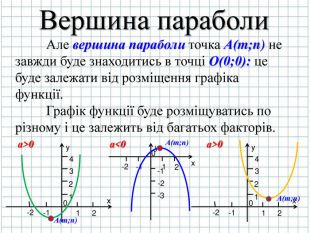
1.Необхідно знайти розміщення вершини параболи точку А(m;n);
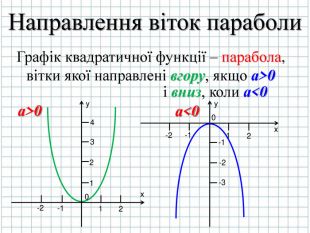
2. Необхідно з'ясувати вгору чи вниз будуть направлені вітки параболи;
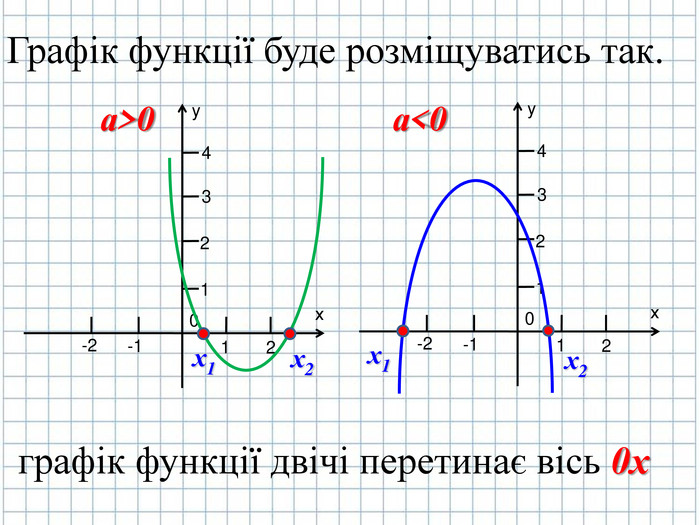
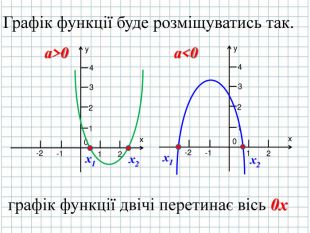
3. Необхідно знайти нулі функції, тобто де графік функції буде перетинатись з віссю абсцис 0х.
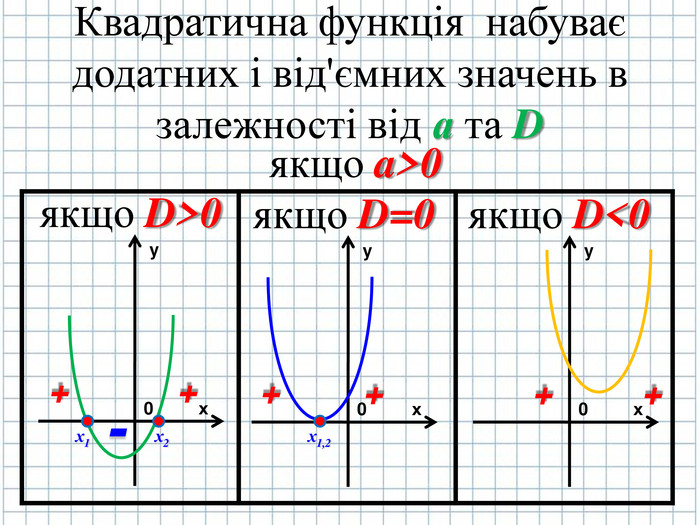
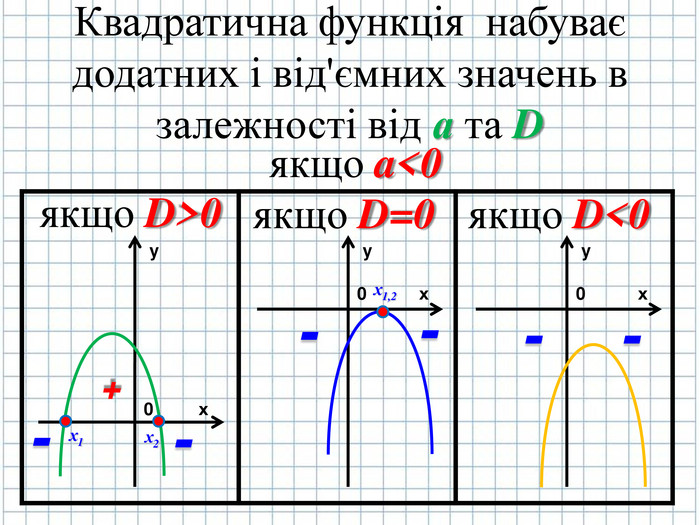
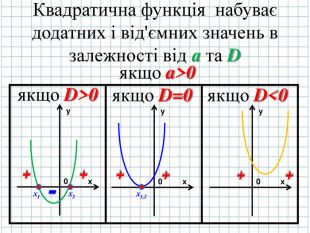
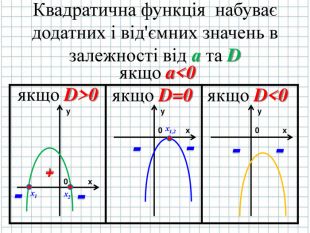
4. Необхідно з'ясувати де в Декартові системі координат квадратична функція буде набувати додатних (+) і від'ємних (-) значень. ( слайд № 5)
Учні отримують пам’ятки.
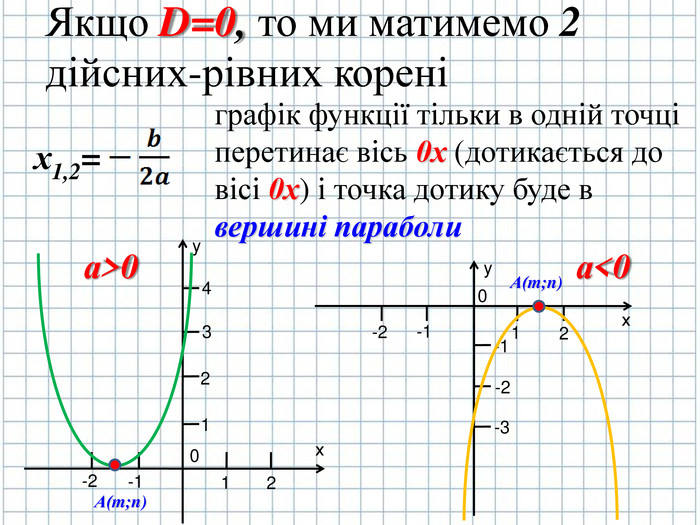
Знайдемо вершину параболи точку А( m,n) (слайд № 6)
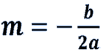
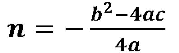
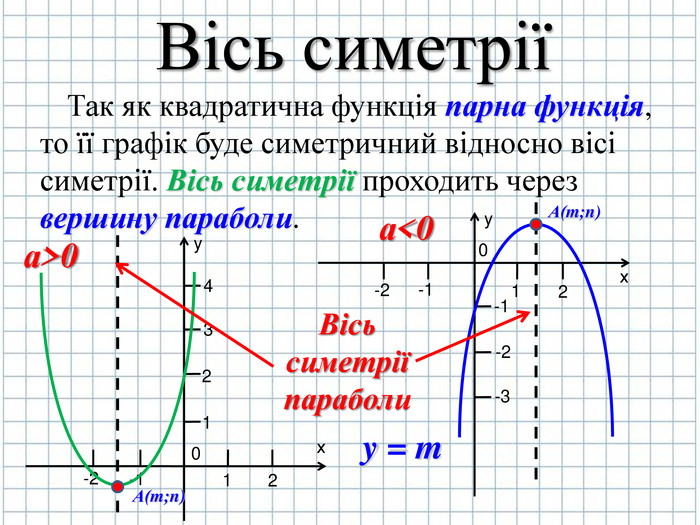
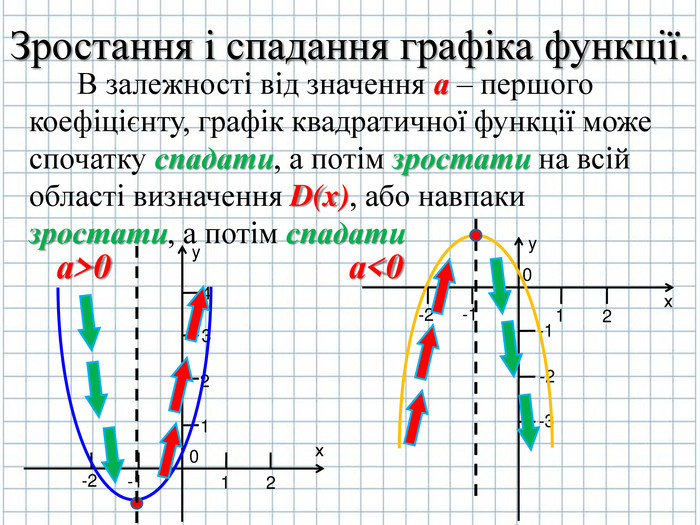
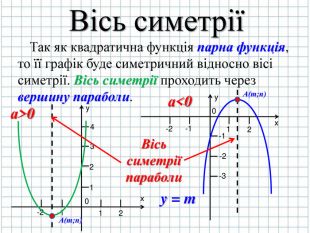
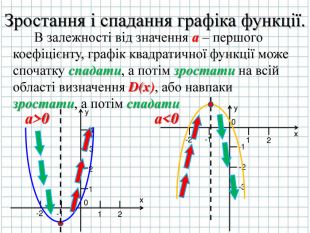
Згадаємо також що функція y = ax2 +bx + c парна функція то це означає що графік функції буде симетричним відносно певної вісі симетрії (слайд № 7)
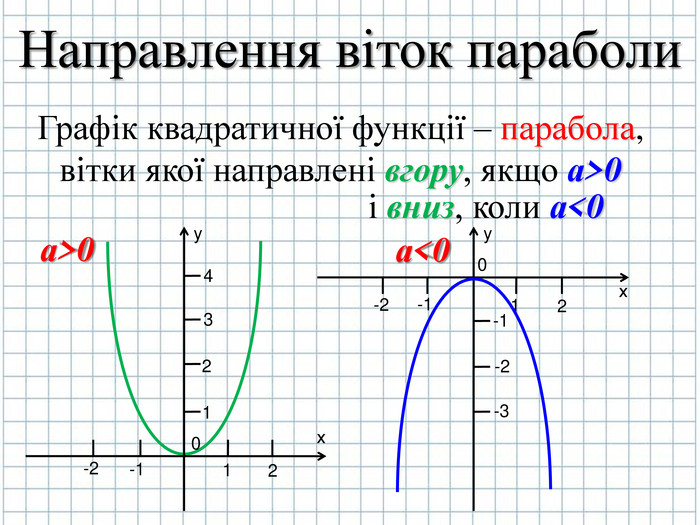
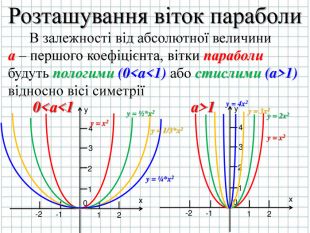
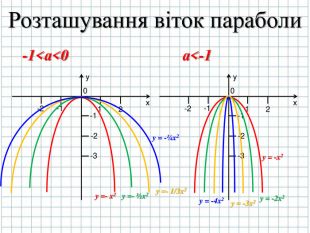
Розглянемо де будуть напрямлені вітки параболи в залежності від значення першого коефіцієнта а (слайд № 8)
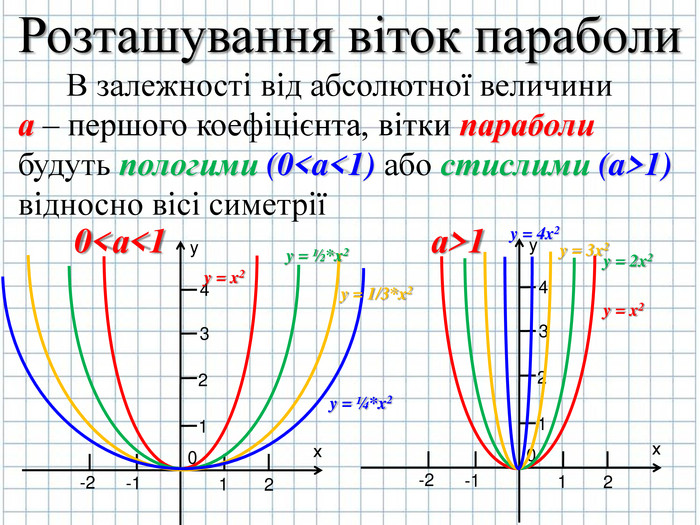
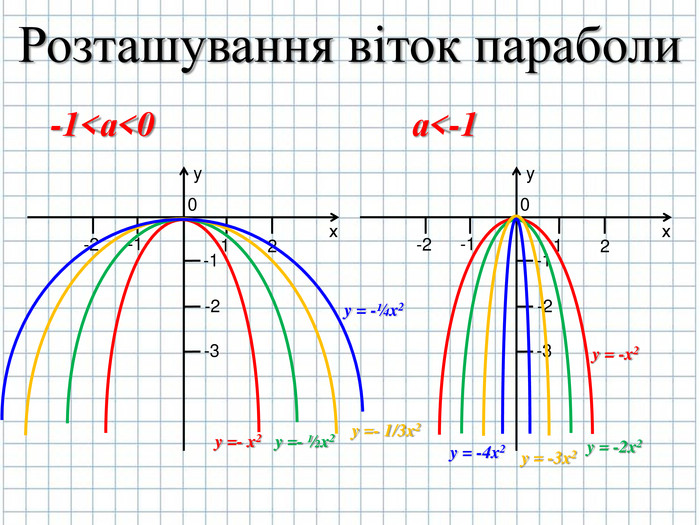
Також нас буде цікавити як вітки параболи будуть розташовані відносно вісі симетрії, вони будуть стислими чи пологими відносно вісі симетрії ( слайд № 9-12)
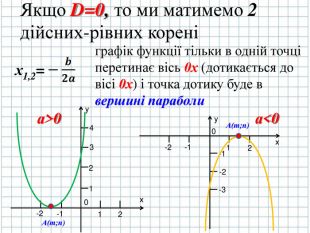
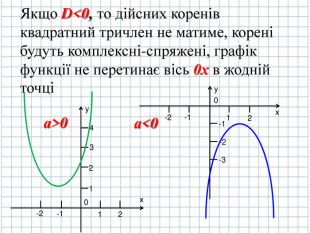
Точки перетину графіка функції з осями симетрії ми можемо знайти за допомогою розв’язку квадратного тричлена, як квадратного рівняння
ax2+bx+c=0
D=b2-4ac
Якщо D>0 х1= ![]() ; х2=
; х2=![]()
Якщо D=0, то х1,2= ![]()
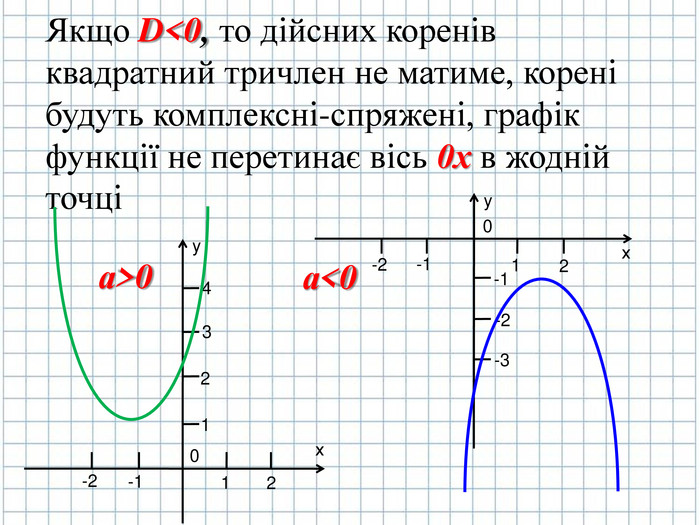
Якщо D<0, то дійсних коренів квадратний тричлен не матиме, корені будуть комплексні-спряжені
(слайди № 13 – 16 )
Квадратична функція в залежності від коефіцієнтів може набувати доданого і від’ємного значення ( слайд № 17,18)
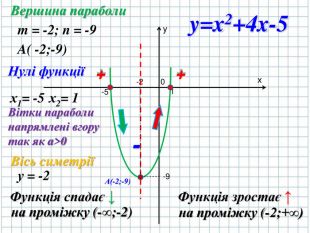
Розглянемо приклад
y=x2+4x-5
Вершина параболи
m = -2; n = -9 A( -2;-9)
Нулі функції х1= -5; х2= 1 ( слайд № 19,20)
Проаналізуємо за нашим планом властивості квадратичної функції та її графік.
ІV. Закріплення знань і умінь.
Робота з підручником
V. Домашине завдання

 _________________________________________________________________________________________________________________________________
_________________________________________________________________________________________________________________________________


про публікацію авторської розробки
Додати розробку