Розв’язування нерівностей з однією змінною (9клас)

Тема. Розв’язування нерівностей з однією змінною (9клас)

Мета:

• відтворити знання про лінійні нерівності з однією змінною; удосконалювати вміння учнів розв'язувати нерівності  з однією змінною, формувати навички самостійної роботи;
• розвивати увагу, пам'ять, мислення, культуру математичного мовлення;
• виховувати самостійність, активність, дисциплінованість, інтерес до математики;
• скласти ситуацію успіху для кожного учня.

Тип уроку: формування  навичок і вмінь.

Обладнання: мультимедійна дошка, проектор, ноутбук; роздавальний матеріал: піктограми настрою, картки контролю знань, картки – лото, картки із завданнями математичного диктанту; мультимедійні презентації.

Хід уроку

І. Створення ситуації успіху, позитивного настрою

Вітання з учнями. Слова учителя: Почати сьогоднішній урок я вирішила зі слів відомого математика Рене Декарта

«Не достатньо мати лише добрий розум,                                                             головне — це раціонально застосовувати  його».

Під час уроку я хочу стежити за емоційним станом класу. Для цього учні мають спеціальні «піктограми настрою»

 

Покажіть, який у вас зараз настрій. Сподіваюсь, що і в кінці уроку ваш емоційний стан буде добрий.

А ще у вас на партах картки самоконтролю, у яких будете виставляти собі одержані бали за кожен вид роботи.

Поверніться до свого товариша по парті, посміхніться. Побажаймо один одному успіху.

Учитель називає тему уроку. Учні записують у зошити дату, тему уроку, продумуючи завдання, які могли б поставити перед собою.

Учитель. Досягти успіху можна тільки тоді, коли є певна мета.

Разом формулюємо навчальну, розвивальну та виховну мету уроку.

Залучити учнів до встановлення завдань, планування діяльності на уроці.

1.        Настрій.
2.        Діагностика виконання домашньої роботи.
3.        Актуалізація опорних знань з теми.
4.        Формування умінь і навичок (типові вправи).
5.        Удосконалення вмінь розв’язувати лінійні нерівності з однією змінною (творчі завдання).
6.        Для роботи вдома.
7.        Підсумки. Висновки. Настрій.

•                Фронтальне опитування у вигляді «Бліц-інтерв’ю»  (учитель ставить запитання і передає «мікрофон» учню, який після відповіді, передає мікрофон наступному учню. За кожну правильну відповідь учень ставить собі у картку контролю 0,5 бали).

Запитання для «Бліц-інтерв’ю»

1. Коли число а вважають більшим від числа в?  А коли меншим?

1. Які знаки використовуються для порівняння двох чисел?
2. Що таке нерівність?
3. Що таке числова нерівність?
4. Назвати знаки строгої та нестрогої нерівності.
5. Сформулювати властивості числових нерівностей.
6. Навести приклад нерівності з однією змінною
7. Що називається розв’язком нерівності з однією змінною?
8. Що означає розв’язати нерівність?
9. Які нерівності називаються рівносильними?
10. Яка нерівність називається лінійною нерівністю з однією змінною? Приклади.
11. Сформулювати властивості нерівностей із змінною. Для чого вони використовуються?
12. Скільки розв’язків може мати нерівність з однією змінною?

• Два учні на дошці розв’язують вправи, аналогічні до домашнього завдання.

 Картка №1

1. Записати всі цілі числа, що належать проміжку: (-1,2; 4]
2. Розв’язати нерівність: 3х+1≥4х-6

Картка №2

1. Записати всі цілі числа, що належать проміжку: [-2; 7)
2.   Розв’язати нерівність: 5х+8≤2-3х

Перевірка, обговорення розв’язків.

Математичний диктант із самоперевіркою і самооцінюванням. Самоперевірка здійснюється за відповідями на екрані. Кожне завдання-1бал.

1.Виберіть правильну числову нерівність:

а)0,2>2; б)-1<-2; в)5≥5;  г) 2,36 ≤ 1,1589.

 2.Сумою нерівностей 5>3і2>-1є нерівність:

 а)4>5;  б)4<5; в)7>2; г) 7≥2

 3.Укажіть строгу нерівність:

 а)15≥5;  б)2≤2; в)7>-2; г)-10≥10.

 4.Нерівність х + 2х + 1 ≤ 0 задовольняє число:

 а) 2; б)1;   в) 0;       г)-1

 5.Скільки цілих чисел задовольняє подвійну

 нерівність -1≤х≤1:

 а) одне;   б) два;   в) три;  г) чотири.

 6.Виберіть проміжок, якому належить число 1,37

 а)[-2;3]; б)(-∞;1,37)_;

 в)(2;1,37); r)(-1,37;1,37).

 7.Виберіть нерівність, яка не має розв’язків:

 а)|х|>-3;     б)х<-3;    в)7-|х|<0;  г)х²<0.

 8.Яке найбільше число є розв’язком нерівності

 х²-2х≥ х² + 2:

 а) 2; 6)1;   в)-1;     г) -2

 9. Знайдіть область визначення функції:

у =

 а) (-∞;0);    б) (-∞;0);   в) [0; +∞],    г] (0, +∞)

Отриману кількість балів учні заносять у картки самоконтролю.

•    «Математичне лото»  -  робота у парах.

Завдання для «Математичне лото»

1. 0,5х-4(х-3)>3х	2. -3х+5≥11	3. 1+2х<7,8
4. 7х-5>3х+7	5. х-15≥4х+3	6. 8+6х≤13+6х
7. 3(х+1)>х+5	8. 2(х-1)+4<х+7	9. -3(2+х)+5х≤2х+1

 Картки з відповіддю

(-∞;)  буква  Л	(-∞;-2]  буква О	(-∞;3,4)  буква М
(3; +∞)  буква О	(-∞;-6]  буква Н	х - будь яке число, буква О
(1;+ ∞)  буква С	(-∞;5)  буква О	х - будь яке число, буква В

 

Учні одержують картки «Математичного лото», в клітинках якого зна­ходяться завдання, що необхідно розв'язати. Учні записують розв'язання в зошити, а знайшовши відповідь, накривають завдання карткою з відповіддю. На звороті кожної картки — буква. Розв'язавши всі завдання, учні одержують ім'я відомого вченого, якому належить вислів: «Матема­тику вже тому вчити треба, що вона розум до ладу приводить» (М. В. Ломоносов). 

 Перші три пари, що виконали завдання правильно ставлять у картку контролю по 3 бали, решта відповідно 2,1,0.

 VІ. Удосконалення вмінь учнів

Творчі завдання (дається 5 хвилин на обдумування і розв’язування на чернетці, потім розв’язуються на дошці)

Використовуємо інтерактивний метод «Коло ідей»

1.         Розв’язати задачу: Туристи мають повернутися на базу не пізніше, ніж через 3 години. На яку відстань вони можуть відплисти за течією річки на моторному човні, якщо його власна швидкість 18км/год, а швидкість течії – 4км/год?

Розв’язання.

Нехай х км – шукана відстань, тоді 18+4=22км/год – швидкість за течією. А 18-4=14 км/год – швидкість проти течії.

Маємо: +≤3,  розв’язавши нерівність, одержимо х ≤ 25 км/год.

2.         Розв’язати нерівність. |1-5х|≤2, 

Розв’язання.  -2≤1-5х≤2,   -3≤-5х≤1,    -1≤5х≤-3,       -≤х≤-.

3.   Знайти допустимі значення змінних виразу : .

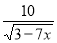4. Знайти найменший натуральний розв’язок нерівності:-3

За кожне завдання, розв’язане  самостійно, учень ставить у картку контролю 3 бали. За подану правильно ідею в розв’язанні - 1 бал.

VІІ. Для роботи вдома.  Достатній рівень: розв’язати нерівність:

  а) 4х>12(3х-1)-16(х+1);

 б) 23+8х≤5х-11.

Високий рівень: написати нерівність із змінною х,  а)яку задовольняє кожне дійсне число; б)яка не має жодного розв’язку.

VІІІ. Самоаналіз уроку.   Метод «Мікрофон»

Запитання:

• Яку мету ставили на початку уроку?
• Чи досягли мети протягом уроку?
• Чи вдалося вам заповнити прогалини в знаннях?
• Чи продук­тивною була ваша робота на уроці?
• Що нового дізналися?
• Чи досягли успіху?

Яку кількість балів одержали на уроці. Виставлення оцінок.

Учитель проводить цінування роботи учнів на уроці.

 

Додаток до уроку:    Картка УСПІХУ

 учня  9 класу________________________________

Вид роботи на уроці	Кількість балів	Учитель
1. Бліц-інтерв’ю
2. Домашнє завдання
3. Математичний диктант
4. Математичне лото
5. Творчі завдання
Сума балів