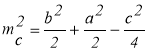ФАКУЛЬТАТИВНИЙ КУРС З МАТЕМАТИКИ “ГЕОМЕТРІЯ ТРИКУТНИКА”
УПРАВЛІННЯ ОСВІТИ І НАУКИ
ДНІПРОПЕТРОВСЬКОЇ ОБЛАСНОЇ ДЕРЖАВНОЇ АДМІНІСТРАЦІЇ
ДНІПРОПЕТРОВСЬКИЙ ОБЛАСНИЙ ІНСТИТУТ ПІСЛЯДИПЛОМНОЇ ПЕДАГОГІЧНОЇ ОСВІТИ
ФАКУЛЬТАТИВНИЙ КУРС З МАТЕМАТИКИ
“ГЕОМЕТРІЯ ТРИКУТНИКА”
10 клас

З досвіду роботи
вчителя математики
Петропавлівської
ЗОШ I-III ступенів
Полозенко К.С.
смт. Петропавлівка
![]() 2010 р.
2010 р.
Зміст
|
1.Пояснювальна записка……………………………………………............... |
3 |
|
2.Вступне заняття……………………………………………......................... |
6 |
|
3. Розділ I.Формули для площ трикутників…………………....................... |
12 |
|
§1.1 Крокуючи за Піфагором……………………………... |
12 |
|
§1.2. Площа трикутника…………………………………... |
24 |
|
4. Розділ II.Навколо чудових точок трикутника……………………….... |
33 |
|
§2.1. Чудові точки. Теорема Чеви……………................... |
33 |
|
§2.2. Теорема Нагеля. Чудові відрізки…………………… |
42 |
|
5. Розділ III. Деякі чудові прямі трикутника……………………............... |
49 |
|
§3.1. Бісектриси …………………………………................ |
49 |
|
§3.2. Медіани та серединний трикутник ………………… |
57 |
|
§3.3. Висоти та ортотрикутник…………………………………….. |
64 |
|
6. Розділ IV. “Світ Ейлера”………………………………………………… |
75 |
|
7. Розділ V. Педальний трикутник………………………………................... |
84 |
|
8. Розділ VI. Прямі Сімсона……………………………….............................. |
91 |
|
9. Розділ VII.Трикутники Наполеона………………..…….......................... |
99 |
|
10. Розділ VIII.Підсумкове заняття……………..………………………….... |
106 |
|
11. Додатки……………………………………………………………………. |
118 |
|
10.1. Додаток А……………………………………………………… |
118 |
|
10.2. Додаток B……………………………………………………… |
129 |
|
10.3. Додаток C……………………………………………………… |
145 |
|
10.4. Додаток D……………………………………………………… |
146 |
|
10.5. Додаток E……………………………………………………… |
147 |
|
11. Програма курсу………………………………………………………….... |
149 |
|
12. Список використаної літератури………………………………………... |
154 |
Пояснювальна записка
Основна функція такого курсу – виявлення засобами предмета математики спрямованості особи, її професійних інтересів. Зміст факультативного курсу не повинен дублювати базовий курс. Його необхідно доповнити елементами, які можуть бути використані для глибшої математичної підготовки школярів. З цієї точки зору великого значення набувають курси, що розширюють базовий курс з математики, дають можливість познайомитися учням з цікавими, нестандартними питаннями.
Програми факультативних курсів включають поглиблення окремих тем базових загальноосвітніх програм з математики, а також вивчення деяких тем, що виходять за межі. Тому вважаємо за доцільне включення наочно-орієнтованого факультативного курсу «Геометрія трикутника» у систему підготовки учнів 10 класу з математики у другому семестрі. Цей курс доповнює базову програму, не порушуючи її цілісності.
Трикутник – одна з основних фігур, що вивчається в геометрії. Вже два з половиною тисячоліття трикутник є її символом, і не лише: трикутник – це атом геометрії.
У розробленому курсі розглядатиметься величезний пласт основних фактів і понять шкільного курсу планіметрії: подібність фігур; властивості і ознаки паралельних прямих; ознаки рівності трикутників; метричні співвідношення в трикутнику, паралелограмі; коло, описане навколо трикутника і вписане в нього тощо. Також наводиться багато нових цікавих понять і різних відомостей з історії, географії, астрономії тощо.
Оскільки на сучасному етапі розвиту освіти інформаційні технології є важливою її складовою, декілька занять розроблені з програмною інформаційно-комунікаційною підтримкою (Додаток А).
Факультативний курс “Геометрія трикутника” розширюватиме світогляд учня та його уявлення про можливості застосування математичного апарату, розвиватиме абстрактно-логічне мислення, створюватиме умови для розвитку творчих здібностей шляхом розв’язання запропонованих автором евристичних задач і формулювання учнями власних. Запропоновані задачі у представленому курсі супроводжуються відповідями (вказівками, розв’язаннями, доведеннями) (Додаток В).
Головним при проектуванні курсу було для нас визначення змісту курсу, знаходження таких прийомів вивчення геометрії, що орієнтуються на саморозвиток учня, дозволяють зробити навчальний матеріал цікавим, максимально наочним і доступним для всіх учнів, підкреслити його міждисциплінарний і практичний характер.
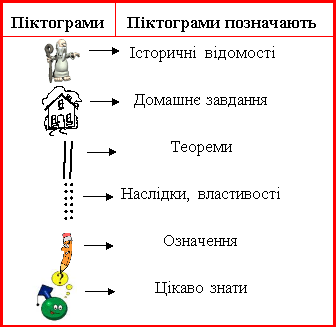
Зміст елективного курсу супроводжується піктограмами (див. табл.).
Мета курсу: розширення геометричного уявлення учнів про властивості трикутника, встановлення міжпредметних зв’язків математики з іншими дисциплінами, розвиток особистості учня.
Вимоги до рівня освоєння змісту курсу
Адміністративної перевірки засвоєння матеріалу з курсу «Геометрія трикутника» не передбачається, відповідні завдання не входять до адміністративних контрольних робіт і не виноситимуться на іспити.
Підсумковий контроль за курсом, пропонується здійснити у вигляді комп’ютерного теста, що розроблений за допомогою програми ИКТС 1.21, і дозволяє миттєво перевірити правильність відповідей (Додаток В на диску). Розподіл годин курсу по темах див. Додаток С.
Вступне заняття
Тема. Перші кроки в світі пізнання трикутників.
Мета: Забезпечення сприйняття учнями цілей вивчення теми.
Обладнання: таблиця, рисунки до задач.
Девіз курсу: «Світ, що нас оточує, – це світ геометрії. Тож давайте його пізнавати!»
Хід уроку.
І. Мотивація
Сьогодні вступний урок з цікавої теми: «Геометрія трикутника» і хочеться розпочати його з висловлень відомих математиків, щодо предмету “геометрія”:
1) Геометрія — це прообраз краси світу.
І. Кеплер
2) Серед рівних розумом — за інших рівних умов — переважає той, хто знає геометрію.
Блез Паскаль.
3) Геометрія — володарка розумових пошуків.
М. Ломоносов
4) Геометрія наближує розум до істини.
Платон
Життя перед людиною постійно ставить задачі…..
Чому в Канаді дитину ставлять на ковзани із найменшого віку? Мабуть, щоб вона не боялась падати, щоб для неї це було майже природно та щоб через певний час дитині було під силу розв’язувати більш складні завдання катання на ковзанах.
За словами Канта: «Якщо дати одну рибину людині, вона буде ситою один день, дати дві рибини – буде ситою два дні, а якщо навчити її ловити рибу, то вона буде ситою все життя».
Так і в геометрії — чим раніше ми познайомимо учня з важливими, корисними і, до того ж, красивими геометричними фактами, тим швидше він відчуватиме себе впевнено при розв’язанні геометричних задач, іноді досить складних. Тим легше буде спонукати дітей до творчості та імпровізацій [40, 11].
Звісно, мета не в тому, щоб усі задачі були доведені до відповіді, а в тому, щоб одержати від цієї задачі користь, тобто просунутися на одну сходинку вище, піднімаючись до вершин.
Чому Олександр Сергійович Пушкін, який не дуже шанував математику, сказав: «У геометрії натхнення таке ж потрібне, як і в поезії»? Чому мова йде про геометрію? Може тому, що вона — Душа математики? А до Душі в усі часи ставлення особливе [4, 9]…
 Щоб краще розібратися про що йдеться, звернемося до історії.
Щоб краще розібратися про що йдеться, звернемося до історії.
Як засвідчує сама назва предмета “геометрія”, спочатку вона становила систему правил і порад для землемірів.
Після Ренесансу геометрія істотно збагатилася новими фактами і методами, виникли: аналітична, проективна, нарисна, диференціальна, неевклідова геометрії, топологія тощо. А від геодезії (практичної геометрії) відокремилась маркшейдерія – та її частина, яка займається вимірюванням шахтних розробок [4, 3].
І тут слід звернути увагу на девіз нашого курсу: «Світ, що нас оточує, – це світ геометрії. Тож давайте його пізнавати!»
Ми з Вами зануримось у таємниці геометричної фігури, що дістала назву «трикутник». Важливу роль відіграватимуть: система геометричних понять, їх означення і класифікації; геометричні величини, їх вимірювання й обчислення; геометричні побудови; перетворення тощо. Ви познайомитесь не тільки з геометричними абстракціями, а й з творцями геометричної науки, з використанням геометрії архітекторами, конструкторами, будівельниками, художниками, працівниками прикладного мистецтва.
Дещо з переліченого ми розглянемо у наступній презентації під назвою “Прикладне застосування трикутників” (Додаток А на діску).
А зараз розглянемо таку задачу (подібну до неї розглядали у презентації):
Визначити висоту телеграфного стовпа А1С1, зображеного на рисунку 1.
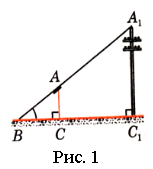
 Для розв’язання цієї задачі необхідно поставити на деякій відстані від стовпа жердину АС з планкою, що обертається, і направити її на верхню точку А1 стовпа. Відмітимо на поверхні землі точку В, в якій пряма А1А перетинається з поверхнею землі. Отримані прямокутні трикутники А1С1В і АСВ подібні за першою ознакою подібності трикутників. Далі, відмірявши відстань ВС1, ВС і знаючи довжину АС жердини, визначаємо висоту А1С1 телеграфного стовпа (через відношення відповідних сторін трикутника).
Для розв’язання цієї задачі необхідно поставити на деякій відстані від стовпа жердину АС з планкою, що обертається, і направити її на верхню точку А1 стовпа. Відмітимо на поверхні землі точку В, в якій пряма А1А перетинається з поверхнею землі. Отримані прямокутні трикутники А1С1В і АСВ подібні за першою ознакою подібності трикутників. Далі, відмірявши відстань ВС1, ВС і знаючи довжину АС жердини, визначаємо висоту А1С1 телеграфного стовпа (через відношення відповідних сторін трикутника).
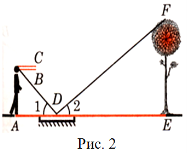
Інший спосіб визначення висоти предмету – це використання дзеркала так, як показано на рисунку 2. Промінь світла, відбиваючись від дзеркала, потрапляє на око людини [39].(Використати подібніcть трикутників – ACD i EFD.)
Для вивчення нового матеріалу та розв’язування задач необхідно узгодити позначення та згадати деякі потрібні надалі формули та формулювання фактів. Тому, проведемо актуалізацію знань.
ІІ. Актуалізація знань
Вчитель роздає учням аркуші з таблицею 1 — основними позначеннями та формулами:
Таблиця 1
|
|
А, В, С – вершини трикутника АВС а, в,с – сторони трикутника АВС α, β, γ – кути трикутника АВС
О – центр описаного кола (точка перетину серединних перпендикулярів) R – радіус описаного кола
р = |
|
|
ОІ – інцентр – центр вписаного кола (точка перетину бісектрис) r – радіус вписаного кола
S∆АВС =
S∆АВС =
|
|
|
Н – ортоцентр (точка перетину висот)
М – центроїд (центр тяжіння) – точка перетину медіан |
|
|
Оа, Ов, Ос – центри зовнівписаних кіл трикутника АВС
ra, rb, rc – радіуси зовнівписаних кіл трикутника АВС |
|
|
|
|
|
трикутник ВАС – прямокутний АО – медіана (ma) ma = R
S∆АВС =
|
|
Теорема косинусів: b2=
Теорема синусів:
|
|
Вчитель разом із учнями розбирають зміст таблиці 1, згадуючи і коментуючи при цьому деякі властивості.
Далі пропонується система задач для перевірки готовності учнів до вивчення нового матеріалу.
|
|
Обчисліть усі невідомі кути трикутника АВС. |
|
|
Чому дорівнює |
|
|
а) Якими є трикутники АОВ і АВС? Поясніть.
б)Чому дорівнює в)Чи можна навколо чотирикутника АОВС описати коло? Поясніть. |
|
|
Обчисліть АВ, якщо ОК = 4см, а ОВ = 5см. Поясніть.
|
![]() ІV. Домашнє завдання
ІV. Домашнє завдання
Вчитель: «На наступному уроці ми завітаємо до Піфагора –розглянемо цікаві факти його життя. Тому завданням буде віднайти як найбільше цікавої інформації про цього відомого математика».
Розділ І. Формули для площ трикутників
§ 1.1
Тема. Крокуючи за Піфагором.
Мета дидактична: узагальнити, систематизувати та закріпити знання учнів про теорему Піфагора; вчити знаходити різні способи доведення цієї теореми; показати застосування набутих знань в практичній діяльності;
розвивальна: розвивати вміння аналізувати, робити висновки, знаходити власні оригінальні способи доведення;
виховна: привчати працювати творчо; виховувати охайність та самостійність.
Обладнання: виготовлені креслення та засоби для показу, портрет Піфагора.
Методика введення теми
- Мотивація
Тема нашого уроку пов’язана з ім’ям великого давньогрецького математика і філософа – Піфагора Самоського (див.рис.) (кінець 580р. – кінець 500 р. до н.е.). Він займався і природничими науками, і теорією музики.
Домашнім завданням було віднайти інформацію про цю велику людину. Тому продовжити мою розповідь я пропоную Вам.
 (слова учнів)
(слова учнів)
 Учень. Піфагор, чиїм іменем названо теорему, жив у VI ст. до н. е. в Давній Греції (народився на острові Самос, тому його називають Піфагором Самоським).
Учень. Піфагор, чиїм іменем названо теорему, жив у VI ст. до н. е. в Давній Греції (народився на острові Самос, тому його називають Піфагором Самоським).
Батьком Піфагора був Мнесарх, різьбяр по дорогоцінному камінні. Ім'я ж матері Піфагора невідоме. Тоді математика у греків тільки складалася у теоретичну науку, і молодий учений мав на неї великий вплив.
Учениця. Піфагор багато подорожував, його ім'я було оточене масою легенд, тому важко визначити, що зробив він сам, а що запозичив у інших. У всякому разі, залежність між сторонами прямокутного трикутника була відома ще за 1000 років до Піфагора в Древньому Вавилоні та Єгипті. Піфагору, очевидно, належить заслуга доведення цієї теореми й широкого застосування її під час розв'язування задач.
(можливе доповнення вчителя)
Про життя Піфагора відомо небагато. Ще у дитинстві він проявляв неабиякі здібності, і коли підріс, невгомонній уяві хлопця стало тісно на маленькому острові.
Піфагор перебрався у місто Мілеєт і став учнем Фалеса, якому на той час йшов восьмий десяток. Мудрий учений порадив хлопцеві відправитися до Єгипту, де сам колись вивчав науки.
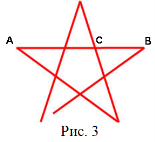 Піфагор відвідав Грецію, де його вразило те, що боги були в образі людей, а єгипетські боги – в образі напівлюдей-напівтварин і побував у Вавилоні, де знайшов місце серед вавилонських мудреців. У сорокалітньому віці Піфагор повернувся на батьківщину і організував таємний союз із молодих представників аристократії. У цей союз вступали з великими церемоніями після довгих випробувань. Кожен, хто вступав, відрікався від свого майна і давав клятву зберігати у таємниці вчення засновника. Піфагорійці, як їх пізніше почали називати, займалися математикою, філософією, природничими науками. Емблемою, або пізнавальним знаком союзу, була пентаграма – п’ятикінцева зірка (рис. 3). Це був геометричний знак п'яти планет (Юпітера, Меркурія, Марса, Сатурну, Венери). Також число променів цієї зірки представлялося піфагорійцями як число кохання: 5 = 2 + 3; 2 – перше жіноче число, 3 – перше чоловіче число. Саме тому пентаграма була символом життя і здоров'я, їй привласнювалася здатність захищати людину від злих духів.
Піфагор відвідав Грецію, де його вразило те, що боги були в образі людей, а єгипетські боги – в образі напівлюдей-напівтварин і побував у Вавилоні, де знайшов місце серед вавилонських мудреців. У сорокалітньому віці Піфагор повернувся на батьківщину і організував таємний союз із молодих представників аристократії. У цей союз вступали з великими церемоніями після довгих випробувань. Кожен, хто вступав, відрікався від свого майна і давав клятву зберігати у таємниці вчення засновника. Піфагорійці, як їх пізніше почали називати, займалися математикою, філософією, природничими науками. Емблемою, або пізнавальним знаком союзу, була пентаграма – п’ятикінцева зірка (рис. 3). Це був геометричний знак п'яти планет (Юпітера, Меркурія, Марса, Сатурну, Венери). Також число променів цієї зірки представлялося піфагорійцями як число кохання: 5 = 2 + 3; 2 – перше жіноче число, 3 – перше чоловіче число. Саме тому пентаграма була символом життя і здоров'я, їй привласнювалася здатність захищати людину від злих духів.
У німецького поета Гете в трагедії “Фауст” описується випадок, коли демон Мефістофель проник в житло вченого Фауста, тому що пентаграма на його будинку була погано накреслена, і в куточку залишився проміжок. Зачитаю вам епізод:
|
Мефістофель: |
Нет, трудновато выйти мне теперь, |
|
Фауст: |
Не пентаграмма ль этому виной? |
|
Мефістофель: |
Изволили ее вы плохо начертить, |
Цей символ з погляду математики цікавий тим, що відношення його відрізків

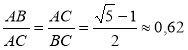
називається «золотим перерізом».
Цей п'ятикутник має цікаву геометричну властивість: поворотну симетрію п'ятого порядку, тобто має п'ять осей симетрії, які співпадають при кожному повороті на 720. Саме цей тип симетрії найбільш поширений в живій природі у квіток незабудки, гвоздики, дзвоника, шипшини (рис. 4), перстачу гусячому (рис.5), вишні (рис. 6), груші, яблуні, малини, горобини тощо. Поворотна симетрія п'ятого порядку зустрічається і у тваринному світі, наприклад, у морської зірки (мал. 7) і панцира морського їжака.
- Засвоєння
Важко знайти людину, у якої ім'я Піфагора не асоціювалося б з – теоремою Піфагора. Сьогодні ми з нею познайомимося ближче. Здавалося б, а що ще цікавого можна дізнатися про теорему Піфагора? Як формулюється знаємо, як доводиться, начебто, теж. Тому зробимо так: я називатиму стверджувальні факти з якими ця теорема пов’язана, а Ви називатимете ті з них, які відомі Вам. Домовились?
Отже,
- теорема Піфагора у учнів середніх віків вважалась дуже важкою і називалась іноді ослиним мостом, або втечею бідних.
 Доповнення: тому що деякі “бідні учні”, які не мали серйозної математичної підготовки, тікали від геометрії. Слабких учнів, які заучували теорему напам’ять без її розуміння називали “ослами”. Вони не в змозі були її “подолати”, тому для них ця теорема була ніби непрохідним мостом.
Доповнення: тому що деякі “бідні учні”, які не мали серйозної математичної підготовки, тікали від геометрії. Слабких учнів, які заучували теорему напам’ять без її розуміння називали “ослами”. Вони не в змозі були її “подолати”, тому для них ця теорема була ніби непрохідним мостом.
- Закінчіть фразу, будь-ласка: “Пифагоровы штаны…”
Доповнення: “…во все стороны равны”. Такі віршики складали учні середніх віків при вивченні теореми Піфагора, і малювали до них шаржі. Наприклад, такі як на рисунку 8.
- Сформулюйте, будь-ласка, теорему Піфагора.
Доповнення: квадрат гіпотенузи дорівнює сумі квадратів катетів. Формулювання цієї теореми є й у віршованій формі:
Если дан нам треугольник
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда легко найдем:
Катеты в квадрат возводим,
Сумму степеней находим –
И таким простым путем
К результату мы придем.
- Теорема Піфагора має більш ніж одне доведення. Скільки?
Доповнення: близько 500 різних доведень. Серед них геометричні, алгебраїчні, механічні тощо.
- Яким методом Ви можете довести цю теорему?
Доповнення: 1. Геометричне д о в е д е н н я
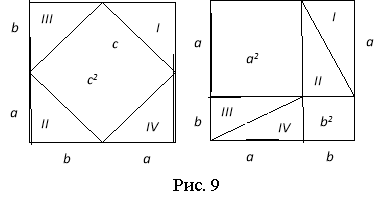
Нехай у прямокутному трикутнику катети дорівнюють а і b, а гіпотенуза с. Побудуємо два квадрати, сторони яких дорівнюють а + b (рис. 9).
![]()
 Очевидно, що площі цих квадратів рівні. Виключаючи трикутники І – IV, бачимо, що с2 = а2 +b2. У першому квадраті виділимо квадрат, побудований на гіпотенузі (дістанемо квадрат і чотири рівні прямокутні трикутники). У другому квадраті виділимо квадрати, побудовані на катетах (дістанемо два квадрати і чотири рівні прямокутні трикутники).
Очевидно, що площі цих квадратів рівні. Виключаючи трикутники І – IV, бачимо, що с2 = а2 +b2. У першому квадраті виділимо квадрат, побудований на гіпотенузі (дістанемо квадрат і чотири рівні прямокутні трикутники). У другому квадраті виділимо квадрати, побудовані на катетах (дістанемо два квадрати і чотири рівні прямокутні трикутники).
Тепер не важко побачити, що площа квадрата, побудованого на гіпотенузі прямокутного трикутника, дорівнює сумі площ квадратів, побудованих на катетах цього трикутника.
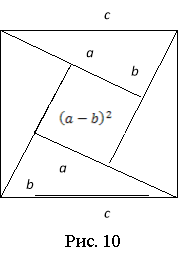
2. Давньоіндійське д о в е д е н н я. У книзі «Вінок знання» індійський математик Бхаскара наводить доведення теореми Піфагора у вигляді креслення (рис.10) з підписом «Дивись!».
Як дістати з креслення Бхаскари доведення теореми Піфагора?
Площа квадрата, побудованого на гіпотенузі с трикутника, рівновелика сумі площ чотирьох прямокутних трикутників і квадрата, довжина сторони якого а – b. Тобто
с2 = ![]() = 2аb+а2 - 2аb+b2 = а2+b2. Звідки с2 = а2+b2.
= 2аb+а2 - 2аb+b2 = а2+b2. Звідки с2 = а2+b2.
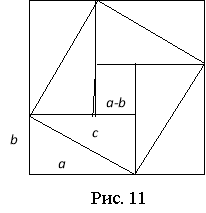 3. Давньокитайське д о в е д е н н я. У коментарі до задачі з «Трактату про мірну віху» квадрат, побудований на сумі катетів a і b прямокутного трикутника, подано як суму площ деяких інших фігур (рис. 11).
3. Давньокитайське д о в е д е н н я. У коментарі до задачі з «Трактату про мірну віху» квадрат, побудований на сумі катетів a і b прямокутного трикутника, подано як суму площ деяких інших фігур (рис. 11).
![]() 4ab + (а – b)2 = 4
4ab + (а – b)2 = 4 ![]() + c2
+ c2
Тому ![]()
![]() .
.
4. Д о в е д е м о теорему методом координат.
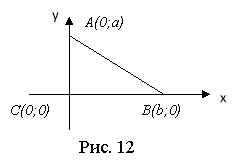 Введемо систему координат: катети трикутника лежать на осях, початок координат у вершині прямого кута.
Введемо систему координат: катети трикутника лежать на осях, початок координат у вершині прямого кута.
Тоді А (0;а), В(b;0), С(0;0). Знайдемо відстані АВ, АС, ВС. Використаємо формулу для обчислення відстані між точками:
![]() , де d – відстань між точками А(х1;у1) і В(х2;у2).
, де d – відстань між точками А(х1;у1) і В(х2;у2).
АВ2 = (0 – b)2 +(a – 0)2 = b 2 +a2, АС2 = (0 – 0)2+(а – 0)2 = а2, BС2 = (b – 0)2 + (0 – 0)2 = b2.
Звідси АВ2 =АС2 +ВС2.
5. Дану теорему можна д о в е с т и і векторним методом (рис.13).
 Нехай
Нехай![]() ,
, ![]() , тобто
, тобто ![]()
![]() Оскільки
Оскільки ![]() то
то ![]() = 0.
= 0.
![]() .
.
![]() =
=![]() +
+![]() = =
= =![]() [40].
[40].
- Застосування
- Застосування теореми Піфагора
а. За її допомогою можна знайти довжини відрізків, не вимірюючи самих відрізків.
Доповнення: наприклад, за допомогою цієї теореми можна знайти діагональ квадрата, прямокутника; висоту трикутника; діагональ куба, паралелепіпеда; висоту піраміди тощо.
Це якби відкриває шлях від прямої до площини, від площини до об’ємного простору тощо. Саме тому теорема Піфагора дуже важлива для людства, яке намагається відкрити все більше вимірів і створити технології в цих вимірах.
Наприклад, у Германії відкрився кінотеатр, де показують кіно в шести вимірах: три були перелічені, а також час, запах і смак. Як це пов’язано з Піфагором? Все дуже “просто”, адже при показі кіно необхідно розрахувати куди і які запахи направляти тощо. Уявіть: на екрані показують джунглі, і Ви відчуваєте запах листя, показують людину, яка обідає, а Ви відчуваєте смак їжі. Захоплює, чи не правда?
b. Теорему застосовують при будівництві споруд.
![]()
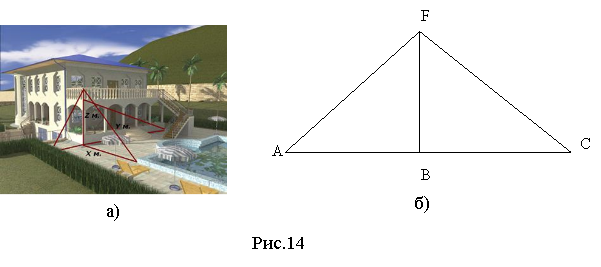 Доповнення: розраховується відстань, центр тяжіння, розташування опор, балок (рис.14-а). Часто постає питання про довжину стропіл для даху, якщо вже виготовлені балки. Наприклад: у будинку задумано побудувати двосхилий дах (форма в перетині). Якої довжини повинні бути стропила, якщо виготовлені балки AС = 8 м і AВ = BF = ВС (рис.14-б).
Доповнення: розраховується відстань, центр тяжіння, розташування опор, балок (рис.14-а). Часто постає питання про довжину стропіл для даху, якщо вже виготовлені балки. Наприклад: у будинку задумано побудувати двосхилий дах (форма в перетині). Якої довжини повинні бути стропила, якщо виготовлені балки AС = 8 м і AВ = BF = ВС (рис.14-б).
Розв’язання.
Трикутник AFC – рівнобедрений. AВ = ВС = 4м, BF = 4 м. Тоді з трикутника FBA: ![]() .
.
c. Теорему застосовують у архітектурі вікон.
Доповнення: У будівлях готичного і романського стилів верхні частини вікон розчленовуються кам'яними ребрами, які не тільки відіграють роль орнаменту, але й сприяють міцності вікон. На рисунку 15 представлений простий приклад такого вікна в готичному стилі. Спосіб побудови його дуже простий. Користуючись рисунком легко знайти центри шести дуг кіл, радіуси яких рівні ширині вікна (b) для зовнішніх дуг і половині ширини (b/2) для внутрішніх дуг. Залишається ще повне коло, що дотикається чотирьох дуг. Оскільки воно розміщене між двома концентричними колами, то його діаметр рівний відстані між цими колами, тобто b/2 і, отже, радіус дорівнює b/4. А тоді, за теоремою Піфагора, можна знайти положення його центру. Вікна в готичному стилі можна побачити у Соборі Паризької Богоматері (рис. 16).
 d. Теорему застосовують у мобільному зв’язку.
d. Теорему застосовують у мобільному зв’язку.
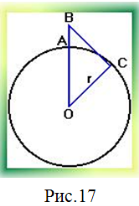 Доповнення: у даний час на ринку мобільного зв'язку йде велика конкуренція серед операторів. Чим надійніший зв'язок, чим більша зона покриття, тим більше споживачів у оператора. При будівництві вежі (антени) часто доводиться вирішувати задачу: яку найбільшу висоту повинна мати антена, щоб передачу можна було приймати в певному радіусі (наприклад радіусі R = 200 км, якщо відомо, що радіус Землі рівний 6380 км).
Доповнення: у даний час на ринку мобільного зв'язку йде велика конкуренція серед операторів. Чим надійніший зв'язок, чим більша зона покриття, тим більше споживачів у оператора. При будівництві вежі (антени) часто доводиться вирішувати задачу: яку найбільшу висоту повинна мати антена, щоб передачу можна було приймати в певному радіусі (наприклад радіусі R = 200 км, якщо відомо, що радіус Землі рівний 6380 км).
Розв’язування
Нехай AВ = x, BС = R = 200 км, OС = r = 6380 км, тоді OB = OA + AB, OB = r + x (рис. 17).
Використовуючи теорему Піфагора, отримаємо відповідь 2,3 км.
- Підведення підсумків
Закінчити наш урок хотілося б з а п о в і д я м и Піфагора:
- Думка – над усе між людьми.
- Знайди собі вірного друга; маючи його, ти можеш обійтися без богів.
- Юні дівчата! Пам’ятайте, що особа лише тоді буває прекрасною, коли вона зображає витончену душу.
- Не ганяйся за щастям: воно завжди знаходиться в тобі самому.
- Роби лише те, що згодом не затьмарить тебе і не змусить розкаюватися.
- Не роби ніколи того, чого не знаєш, але навчися всьому, що потрібно знати.
- Не нехтуй здоров'ям свого тіла.
- Навчися жити просто і без розкоші.
- Через ваги не крокуй – уникай пожадливості.
- Не сідай на хлібну міру – не живи дозвільно.
- Або мовчи, або говори те, що цінніше за мовчання.
- Ластівок в будинку не тримай – не приймай гостей балакучих і не стриманих на мову.
![]() - Не закривай очі, коли хочеш спати, не розібравши всіх своїх вчинків за день.
- Не закривай очі, коли хочеш спати, не розібравши всіх своїх вчинків за день.
- .Домашнє завдання
Розв’яжіть наступні історичні задачі:
|
|
XII століття Бхаскари
|
|
|
|
"Є водоймище шириною в 1 чжан = 10 чи. В його центрі росте очерет, який виступає над водою на 1 чи. Якщо потягнути очерет до берега, то він якраз торкнеться його. Запитується: яка глибина води і яка довжина очерету?" |
|
|
|
Є бамбук заввишки в 1 чжан. Вершину його зігнули так, що вона дотикається землі на відстані 3 чи від кореня (1 чжан = 10 чи). Яка висота бамбука, після того як його зігнули?
|
|
|
|
На глибині 12 футів росте лотос з 13-футовим стеблом. Визначте, на яку відстань квітка може відхилитися від вертикалі, що проходить через точку кріплення стебла до дна. |
|
|
|
Трапилось деякій людині до стіни драбину поставити. Висота тієї стіни є 117 стоп, а драбина завдовжки 125 стоп. І необхідно дізнатись, скільки стоп між нижнім кінцем драбини і стіною. |
§1.2
Тема. Площа трикутника.
Мета дидактична: узагальнити, звести в систему знання та вміння учнів з теми «Площа трикутника»; розширити область їх застосування; ознайомити з цікавими математичними відкриттями;
розвивальна: розвивати навички узагальнення та порівняння, логічне мислення, обчислювальні навички;
виховна: виховувати почуття колективізму, охайність, математичну культуру.
Обладнання: карта світу; плакат з епіграфом уроку; роздатковий матеріал; таблиця з формулами.
Методика введення теми
- Мотивація.
Учитель перевіряє домашнє завдання, відповідає на питання учнів.

 Після цього вчитель нагадує, що більшість доведень теореми Піфагора проводились із використанням формули площі прямокутного трикутника, тому доречно розширити відомості про формули обчислення площі будь-якого трикутника.
Після цього вчитель нагадує, що більшість доведень теореми Піфагора проводились із використанням формули площі прямокутного трикутника, тому доречно розширити відомості про формули обчислення площі будь-якого трикутника.
Учитель: Почнемо з того, що здійснимо подорож. Погляньмо на рисунок 18! На глобусі відмічено такі священні місця: гора Кайлас – рукотворна, священна гора висотою 6666 км, єдина гора, на яку ніколи не ступала нога людини (рис.19); мексиканські піраміди – піраміда Сонця та піраміда Місяця (коли зійдеш на піраміду Сонця, то треба дивитися на Сонце, а якщо на піраміду Місяця – то на Місяць, тому в мексиканських пірамід верхи обрізані) (рис.20); єгипетські піраміди – великі кам'яні блоки, покладені один на одного, що були принесені за десятки кілометрів, а сфінкс, який охороняє піраміду (рис.21), був побудований єгиптянами 4–5 тис. років тому; кажуть, що сфінкс дивиться саме на те місце, де на Землю сходили боги, тобто на схід, де знаходиться Тибет; Стоунхендж – споруда складається з великого каміння, яке встановлено одне на одне, це «висяче каміння» знаходиться у Великій Британії (рис.22); о. Пасхи – на ньому знаходяться великі кам'яні статуї (рис.23) та Бермудські острови (рис.24) – у районі Бермудського трикутника був о. Платона, який поглинуло море 12 000 років тому. Ви запитаєте, а до чого тут це? “Якщо на карті сполучити Кайлас з мексиканськими пірамідами та о. Пасхи, то отримаємо трикутник, що займає ![]() земної кулі. Якщо сполучити мексиканські піраміди з єгипетськими, то ця
земної кулі. Якщо сполучити мексиканські піраміди з єгипетськими, то ця ![]() земної кулі розділиться на два рівні трикутники. Відстані «Кайлас – єгипетські піраміди» та «о. Пасхи – мексиканські піраміди» становлять
земної кулі розділиться на два рівні трикутники. Відстані «Кайлас – єгипетські піраміди» та «о. Пасхи – мексиканські піраміди» становлять ![]() довжини лінії «Кайлас – о. Пасхи». Складається враження, що на Землі існує сувора пірамідально-географічна схема, яка утворена пірамідами та загадковими спорудами давнини. Якщо сполучити Кайлас зі Стоунхенджем, то лінія виводить на о. Пасхи. І ця відстань дорівнює
довжини лінії «Кайлас – о. Пасхи». Складається враження, що на Землі існує сувора пірамідально-географічна схема, яка утворена пірамідами та загадковими спорудами давнини. Якщо сполучити Кайлас зі Стоунхенджем, то лінія виводить на о. Пасхи. І ця відстань дорівнює ![]() відстані «Кайлас – о. Пасхи», а ще через
відстані «Кайлас – о. Пасхи», а ще через ![]() частини на цій самій лінії розміщується Бермудський трикутник. До потопу Північний полюс розміщувався в районі Тибету. Після потопу вісь Землі змістилася на 60°. То чи не була гора Кайлас точкою давнього Північного полюса? Лінія, яка сполучає Кайлас з мексиканськими пірамідами, проходить через Північний полюс” [43]. Ці назви – це географічні назви вершин трикутників, площу яких Ви маєте знайти. І для початку пропоную згадати відомі Вам формули площі трикутника (учням на першому занятті була роздана таблиця 1).
частини на цій самій лінії розміщується Бермудський трикутник. До потопу Північний полюс розміщувався в районі Тибету. Після потопу вісь Землі змістилася на 60°. То чи не була гора Кайлас точкою давнього Північного полюса? Лінія, яка сполучає Кайлас з мексиканськими пірамідами, проходить через Північний полюс” [43]. Ці назви – це географічні назви вершин трикутників, площу яких Ви маєте знайти. І для початку пропоную згадати відомі Вам формули площі трикутника (учням на першому занятті була роздана таблиця 1).
Подивіться уважно на плакат (табл.2). Наведені тут формули є мало- або зовсім невідомими Вам формулами для площі трикутника.
![]() З метою поєднання таблиці 1 і таблиці 2 доведемо (1) та (2) формули з таблиці 1 і перейдемо до таблиці 2. Це дозволить нам застосовувати їх при розв’язанні вище згадуваних задач.
З метою поєднання таблиці 1 і таблиці 2 доведемо (1) та (2) формули з таблиці 1 і перейдемо до таблиці 2. Це дозволить нам застосовувати їх при розв’язанні вище згадуваних задач.
|
|
|
|
|
(4) |
|
|
(5) |
|
|
(6) |
|
|
(7) |
|
|
(8) |
|
|
(9) |
|
|
(10) |
|
|
(11) |
|
|
(12) |
Доведення формули (1). Необхідно згадати теорему синусів:
(13) ![]() ,
,
і відому Вам формулу площі трикутника через дві сторони і кут між ними
(14) ![]() .
.
 З формули (13) нам знадобиться лише підкреслене. Виражаємо
З формули (13) нам знадобиться лише підкреслене. Виражаємо ![]() , і підставляємо у (14), маємо
, і підставляємо у (14), маємо
![]() [11, 32].
[11, 32].
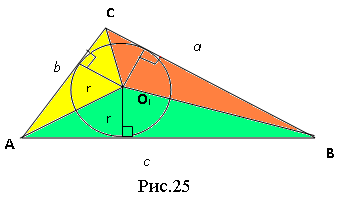
Доведення формули (2). Розглянемо рисунок 25.
Звернемо увагу на площі трикутників АОIС, СОIВ, ВОIА. Сума їх площ буде дорівнювати площі трикутника АВС.
![]()
![]()
 =
=![]() [11, 35].
[11, 35].
Доведення формули (3). Знову скористаємося формулою (13):
![]() ,
, ![]() ,
,
і підставимо ці вирази в (14):
![]() [49, 8].
[49, 8].
Доведення формули (4). З формули (13) маємо:
![]() ,
,
тому ![]() . Підставимо вираз для b в (14), отримаємо
. Підставимо вираз для b в (14), отримаємо
![]() . [49, 8]
. [49, 8]
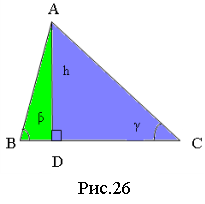 Доведення формули (5). Розглянемо площі трикутників АDC, ADB (рис.26). Сума площ цих трикутників буде дорівнювати площі трикутника АВС.
Доведення формули (5). Розглянемо площі трикутників АDC, ADB (рис.26). Сума площ цих трикутників буде дорівнювати площі трикутника АВС.
Знайдемо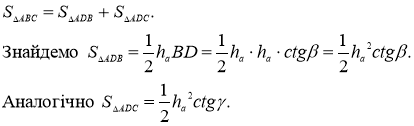 Тоді отримаємо, що
Тоді отримаємо, що ![]() [19, 54].
[19, 54].
Доведення формули (6). Ви знаєте такі формули для обчислення площі трикутника:
(15) ![]()
Перемножимо ліві і праві частини в цих формулах:
![]() З формули (1) виразимо abc:
З формули (1) виразимо abc: ![]() і підставимо у попереднє рівняння:
і підставимо у попереднє рівняння: ![]()
Звідки отримаємо: 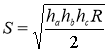 [19, 63].
[19, 63].
Доведення формули (7). Виразимо з формули (15) ![]() :
:
![]() ,
, ![]() ,
, 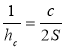 і підставимо у праву частину формули (7),
і підставимо у праву частину формули (7),
маємо: 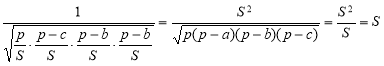 [13, 57].
[13, 57].
Доведення формули (8). Розглянемо рисунок 27. Можна побачити, що
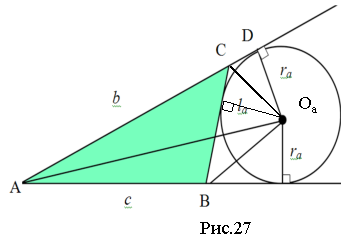
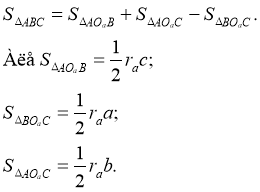
Тоді отримуємо:
![]() [11, 41].
[11, 41].
Доведення формули (9). З формули (8) виражаємо ![]() :
:
(16) 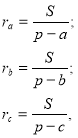
а з формули (2) ![]() . Підставимо отримані вирази в праву частину формули (9):
. Підставимо отримані вирази в праву частину формули (9):
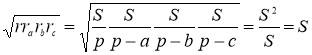 [19, 57].
[19, 57].
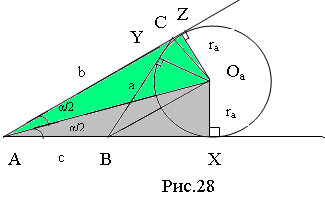 Доведення формули (10). З трикутників AXOa і AZOa (рис.28) виразимо XOa і ZOа, тобто ra :
Доведення формули (10). З трикутників AXOa і AZOa (рис.28) виразимо XOa і ZOа, тобто ra : 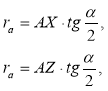 відповідно.
відповідно.
Складемо отримані рівняння:
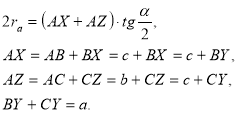
Тоді ![]()
Підставимо в (16): ![]() [19, 57].
[19, 57].
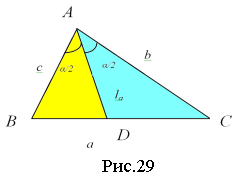 Доведення формули (11). Знову розглянемо площу трикутника АВС, як суму площ трикутників АВD і ADC (рис.29).
Доведення формули (11). Знову розглянемо площу трикутника АВС, як суму площ трикутників АВD і ADC (рис.29).
![]()
![]()
Тоді ![]() [19, 99].
[19, 99].
![]()
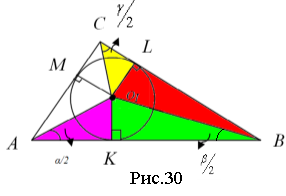 Доведення формули (12). Розіб’ємо
Доведення формули (12). Розіб’ємо ![]() на 6 трикутників (рис.30), і знайдемо лощі:
на 6 трикутників (рис.30), і знайдемо лощі:
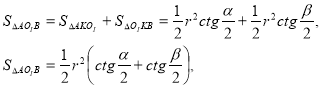
або з формули (5)
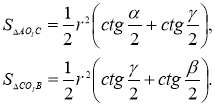
Тому 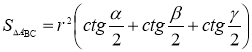 [19, 57].
[19, 57].
- Застосування
 Тепер ми переходимо до розв’язування задач.
Тепер ми переходимо до розв’язування задач.
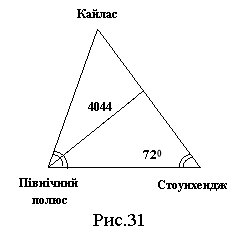
Задача №1.2.1. Якщо з’єднати між собою Кайлас, Північний полюс та Стоунхендж, то отримаємо рівнобедрений трикутник (кути при основі дорівнюють 720). Бісектриса цього кута має довжину 4044 км. Знайдіть площу вищевказаного трикутника, якщо відношення його основи до бічної сторони дорівнює ![]() (рис.31).
(рис.31).
Задача №1.2.2. Якщо з’єднати між собою Єгипетські піраміди, Північний полюс та Стоунхендж, то отримаємо рівнобедрений трикутник (кути при основі дорівнюють 330). Відстань від Єгипетських пірамід до Північного полюсу дорівнює 6666 км. Знайдіть площу вищевказаного трикутника (рис.32).
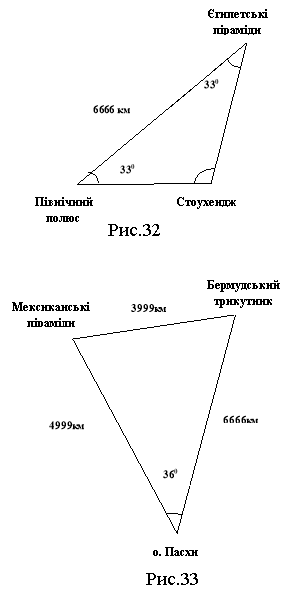 Задача №1.2.3. Якщо з’єднати між собою Мексиканські піраміди, Бермудський трикутник та о. Пасхи, то отримаємо трикутник зі сторонами 3999 км, 6666 км і 4999км відповідно (рис.33). Кут при вершині о. Пасхи має величину 360. Знайдіть площу вищевказаного трикутника.
Задача №1.2.3. Якщо з’єднати між собою Мексиканські піраміди, Бермудський трикутник та о. Пасхи, то отримаємо трикутник зі сторонами 3999 км, 6666 км і 4999км відповідно (рис.33). Кут при вершині о. Пасхи має величину 360. Знайдіть площу вищевказаного трикутника.
-
 Домашнє завдання
Домашнє завдання
Задача №1.2.4. Медіана m поділяє прямий кут у відношенні 1:2. Знайдіть площу трикутника [49, 9].
Задача №1.2.5. Доведіть, що сума відстаней від будь-якої точки всередині правильного трикутника до його сторін дорівнює висоті цього трикутника [49, 9].
Задача №1.2.6. Коло радіуса R проходить через вершини А і В трикутника АВС і дотикається прямої АС у точці А. Знайдіть площу трикутника АВС, якщо кут А дорівнює α, кут В – β [49, 19].
Задача №1.2.7. У прямокутному трикутнику АВС з прямого кута С проведено бісектрису СL,│СL│=а і медіану СМ, │СМ│=b . Знайдіть площу трикутника АВС [49, 22].
Розділ ІI. Навколо чудових точок трикутника
§2.1
Тема: Чудові точки. Теорема Чеви.
Мета дидактична: ознайомити учнів з поняттям “чудові точки”, звести нові знання у чітку систему;
розвивальна: розвивати пізнавальну діяльність, спостережливість, увагу, ініціативність;
виховна: виховувати інтерес до нових знань і прагнення їх набувати.
Обладнання: геометричні рисунки; портрети Джованні Чеви, Лазара Карно.
 Методика введення теми
Методика введення теми
- Вступ
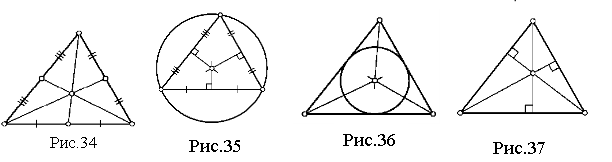
Після організаційного моменту та перевірки домашнього завдання учитель звертається до учнів: спробуймо зрозуміти, а чому той або інший результат геометрії трикутника діє на нас по різному. Узагалі кажучи відповідь на це питання наступна: красива теорема в геометрії трикутника пов'язана, як правило, з чудовими точками, прямими або колами. Але пряма або коло чудові, якщо містять які-небудь чудові точки трикутника. Отже, головними є точки. Але як порівнювати ступінь їх «чудовості» між собою? Очевидно, точка є “більш чудовою”, коли пов’язана з природними та змістовними конфігураціями трикутника. Тому у перший ряд слід поставити, звичайно, таких заслужених “ветеранів” (оскільки ці точки зустрічаються ще у Евкліда), як М – точку перетину медіан (центр тяжіння, центроїд або барицентр) рис. 34, О – центр описаного кола, рис. 35, ОI – центр вписаного кола, рис. 36, Н – точку перетину висот (ортоцентр), рис. 37. Цими точками вичерпується поняття чудових точок. Проте не зіпсує загальної картини і “молодь” (були відкриті близько 200 років тому): точка G Жергонна (рис. 38) і точка N Нагеля (рис. 39).
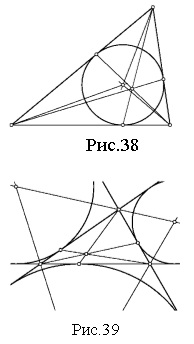
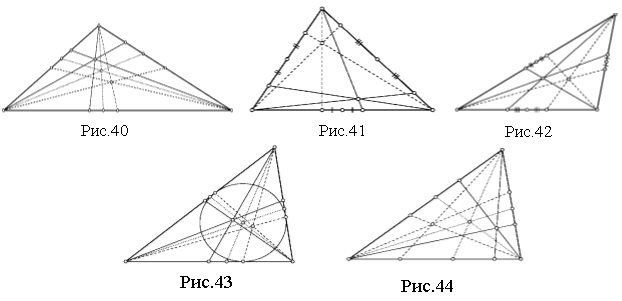
 Також, до спеціальних точок можна віднести точки, які є “похідними” від вищевказаних точок. Тобто отримані з них у результаті якого-небудь перетворення або як перетин яких-небудь чудових ліній першого порядку і так далі. Сюди можна віднести, в першу чергу, точку L Лемуана (точку перетину прямих, симетричних медіанам відносно відповідних бісектрис, таке перетворення називається ізогональним спряженням), рис. 40, антиортоцентр трикутника Нm (точку перетину прямих, що проходять через точки, симетричні основам висот відносно відповідних середин сторін, і протилежні вершини, це перетворення називається ізотомічним спряженням), рис. 41, точку Im перетину антибісектрис (ізотомічно спряжену точці перетину бісектрис), рис. 42, точки Gl і N1 (точки, ізогонально спряжені точкам Жергонна і Нагеля), рис. 43 і 44. Точки третього порядку визначаються аналогічно, як «похідні» точок другого порядку і так далі. Зрозуміло, що із зростанням порядку кількість точок стрімко зростає, а це веде за собою стрімке погіршення їх якості: чим вищий порядок, тим менш виразними є геометричні зв'язки між ними.
Також, до спеціальних точок можна віднести точки, які є “похідними” від вищевказаних точок. Тобто отримані з них у результаті якого-небудь перетворення або як перетин яких-небудь чудових ліній першого порядку і так далі. Сюди можна віднести, в першу чергу, точку L Лемуана (точку перетину прямих, симетричних медіанам відносно відповідних бісектрис, таке перетворення називається ізогональним спряженням), рис. 40, антиортоцентр трикутника Нm (точку перетину прямих, що проходять через точки, симетричні основам висот відносно відповідних середин сторін, і протилежні вершини, це перетворення називається ізотомічним спряженням), рис. 41, точку Im перетину антибісектрис (ізотомічно спряжену точці перетину бісектрис), рис. 42, точки Gl і N1 (точки, ізогонально спряжені точкам Жергонна і Нагеля), рис. 43 і 44. Точки третього порядку визначаються аналогічно, як «похідні» точок другого порядку і так далі. Зрозуміло, що із зростанням порядку кількість точок стрімко зростає, а це веде за собою стрімке погіршення їх якості: чим вищий порядок, тим менш виразними є геометричні зв'язки між ними.
Чудові точки трикутника можуть бути отримані за допомогою наступної процедури.
Нехай у нас є деяке правило, згідно якому ми зможемо вибрати певну точку X на стороні ВС трикутника АВС (або її продовженні). Далі будуємо аналогічні точки Y, Z на двох інших сторонах трикутника. Якщо правило вибору вдале, то прямі АX, ВY, СZ будуть перетинатися в деякій точці К. Наприклад, усі чудові та спеціальні точки рис. 34, рис. 36 – рис. 44 отримуються саме так.
Постає питання: чи можна знайти який-небудь загальний метод, завдяки якому можна було б по положенню точок на сторонах трикутника визначити
|
|
перетинається відповідна трійка прямих в одній точці чи ні.
- Засвоєння
![]() Теорема Чеви: якщо три чевіани AX, BY, CZ перетинаються в одній точці, то відношення, у якому їх основи X, Y і Z ділять сторони трикутника, задовольняють рівності
Теорема Чеви: якщо три чевіани AX, BY, CZ перетинаються в одній точці, то відношення, у якому їх основи X, Y і Z ділять сторони трикутника, задовольняють рівності
![]() [4, 286] (1)
[4, 286] (1)
Рівняння (1) називається умовою Чеви.
Доведення 1. Необхідна умова.
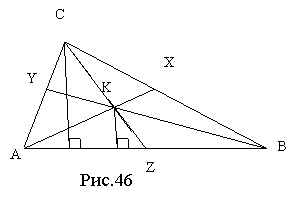 Маємо перетин чевіан в одній точці, треба довести вірність рівності (1).
Маємо перетин чевіан в одній точці, треба довести вірність рівності (1).
Запишемо відношення відрізків ![]() через співвідношення площ.
через співвідношення площ.
Розглянемо трикутники AZC і BZC. Вони мають спільну висоту (рис.46)
![]() ,
, ![]() ,
,
тоді ![]() , (оскільки аналогічною є ситуація і з трикутниками AZK і BZK)
, (оскільки аналогічною є ситуація і з трикутниками AZK і BZK)
Звернемось до співвідношень вигляду:
![]() , тоді
, тоді ![]() ,
, ![]() . Отже,
. Отже, ![]() (перевірити самостійно).
(перевірити самостійно).
Переходячи до площ трикутників, маємо: ![]() .
.
Аналогічно ![]() ,
, ![]() .
.
Отримані рівності перемножуємо і одержуємо необхідне.
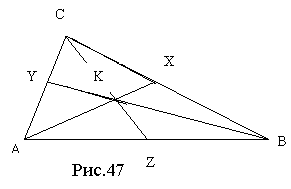 2. Достатня умова.
2. Достатня умова.
З умови Чеви (1) довести, що чевіани перетинаються в одній точці.
Від супротивного: нехай дві чевіани AX і BY перетинаються в точці K і CZ через точку K не проходить за припущенням (рис.47). Проведемо третю чевіана – CZ′ через точку K. Покажемо, що Z′= Z.
Згідно необхідної умови теореми Чеви виконується рівність ![]() , а за умовою (1)
, а за умовою (1) ![]() . Порівняємо ці рівності. Маємо, що
. Порівняємо ці рівності. Маємо, що
(2) ![]() .
.
Розглянемо випадки: 1)точка Z лежить лівіше від Z′;
2) точка Z лежить правіше від Z′.
У 1) випадку ![]() і
і ![]() , тоді
, тоді ![]() .
.
У 2) випадку ![]() і
і ![]() , тоді
, тоді ![]() . А це суперечить умові (2). Тому Z=Z′ [17, 15-16].
. А це суперечить умові (2). Тому Z=Z′ [17, 15-16].
![]() Теорема Чеви у формі синусів
Теорема Чеви у формі синусів
Умову Чеви можна записати також у вигляді
![]() .
.
Доведення еквівалентності цих умов не є складним. Дійсно, застосувавши теорему синусів до трикутників АСZ і BCZ, маємо:
![]() і
і ![]() .
.
Поділивши одну рівність на іншу, матимемо:
![]() .
.
Аналогічно ![]() ,
, ![]() . Врешті-решт отримуємо:
. Врешті-решт отримуємо:
![]() [30, 8-9].
[30, 8-9].
![]() Наслідки
Наслідки
I: три бісектриси трикутника перетинаються в одній точці (рис.36)
(вказівка: застосувати теорему Чеви у формі синусів);
II: три медіани трикутника перетинаються в одній точці (рис.34)
(вказівка: застосувати умову Чеви);
III: три висоти трикутника перетинаються в одній точці (рис.37)
(вказівка: застосувати умову Чеви у формі синусів з використанням відомого співвідношення ![]() записати у вигляді
записати у вигляді ![]() );
);
IV: три серединних перпендикуляри перетинаються в одній точці (рис.35).
![]() Домашнім завданням буде довести перші три наслідки, користуючись вказівками.
Домашнім завданням буде довести перші три наслідки, користуючись вказівками.
А зараз ми детальніше розглянемо IV наслідок. Очевидно, що два серединні перпендикуляри до сторін трикутника перетинаються в точці, рівновіддаленій від усіх трьох вершин трикутника, а тому, ця точка лежить і на третьому серединному перпендикулярі.
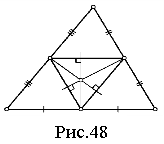 Але як довести цей нескладний факт, користуючись теоремою Чеви? З принципових міркувань хотілося б довести цей факт, але тут виникають труднощі, оскільки за природою своєю теорема Чеви створена для виявлення перетину в одній точці чевіан, а не перпендикулярів до сторін трикутника. Таке ускладнення можна подолати, якщо розглянути трикутник, вершинами якого будуть основи серединних перпендикулярів (рис.48, серединний трикутник — з ним познайомимося далі). Оскільки середні лінії паралельні сторонам вихідного трикутника, серединні перпендикуляри є висотами серединного трикутника. І ми звели завдання до попереднього III наслідку [30, 9].
Але як довести цей нескладний факт, користуючись теоремою Чеви? З принципових міркувань хотілося б довести цей факт, але тут виникають труднощі, оскільки за природою своєю теорема Чеви створена для виявлення перетину в одній точці чевіан, а не перпендикулярів до сторін трикутника. Таке ускладнення можна подолати, якщо розглянути трикутник, вершинами якого будуть основи серединних перпендикулярів (рис.48, серединний трикутник — з ним познайомимося далі). Оскільки середні лінії паралельні сторонам вихідного трикутника, серединні перпендикуляри є висотами серединного трикутника. І ми звели завдання до попереднього III наслідку [30, 9].
Є і змістовніший підхід до цієї проблеми.
|
|
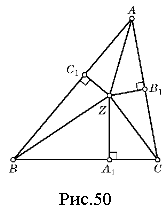
![]() Теорема Карно. Нехай точки А1, В1, С1 лежать на прямих ВС, СА, АВ відповідно. Нехай також ВА1 = х1, СА1 = х2, СВ1 = у1, АВ1 = у2, АС1 = z1, ВC1= z2. Тоді наступні умови рівносильні:
Теорема Карно. Нехай точки А1, В1, С1 лежать на прямих ВС, СА, АВ відповідно. Нехай також ВА1 = х1, СА1 = х2, СВ1 = у1, АВ1 = у2, АС1 = z1, ВC1= z2. Тоді наступні умови рівносильні:
- перпендикуляри до відповідних сторін трикутника проведені з точок А1, В1, С1, перетинаються в одній точці;
-
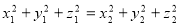 (умова Карно).
(умова Карно).
(Порівняйте з умовою Чеви: х1у1z1 = х2у2z2.)
Доведення спирається лише на теорему Піфагора. Нехай перпендикуляри перетинаються в точці Z. Маємо такі рівності (рис.50):
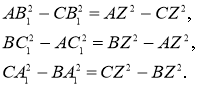
Додаємо їх, і отримуємо умову Карно.
Доведення оберненої теореми Карно (як і оберненої теореми Чеви) використовує пряму теорему: нехай два перпендикуляра перетинаються у деякій точці, опустимо з неї перпендикуляр на третю сторону, запишемо умову Карно і діємо подібно до попередньої теореми.
З теореми Карно наслідок про перетин в одній точці серединних перпендикулярів отримується так же легко, як і II наслідок [30, 10].
- Застосування
|
|
![]() Теорема Жергонна: якщо точки X, Y, Z є точками дотику вписаного кола, то відрізки AX, BY і CZ перетинаються в одній точці G, точці Жергонна, яка в свою чергу не є центром цього кола (рис.51).
Теорема Жергонна: якщо точки X, Y, Z є точками дотику вписаного кола, то відрізки AX, BY і CZ перетинаються в одній точці G, точці Жергонна, яка в свою чергу не є центром цього кола (рис.51).
Доведення (за теоремою Чеви).
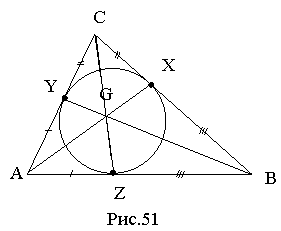
![]() Якщо розглянути відрізки AY і AZ, CY і CX, BX і BZ, то можна сказати, що вони між собою рівні, як дотичні, проведені з однієї точки до кола. Тому буде виконуватись умова Чеви Отже, відрізки AX, BY і CZ мають спільну точку [30, 10].
Якщо розглянути відрізки AY і AZ, CY і CX, BX і BZ, то можна сказати, що вони між собою рівні, як дотичні, проведені з однієї точки до кола. Тому буде виконуватись умова Чеви Отже, відрізки AX, BY і CZ мають спільну точку [30, 10].
-
 Домашнє завдання (додаткове).
Домашнє завдання (додаткове).
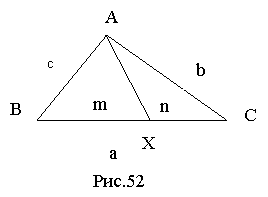
Задача 2.1.1. Нехай AX — чевіана довжиною p, причому BX = m i XC = n, як на рисунку 52. Доведіть, що є вірною рівність
![]() [17, 17].
[17, 17].
|
|
Задача 2.1.2. Доведіть, що середини основ трапеції, точка перетину її діагоналей і точка перетину продовжень бічних сторін лежать на одній прямій [9, 240-241].
§2.2
Тема. Теорема Нагеля. “Чудові відрізки”.
Мета дидактична: узагальнити, систематизувати раніше засвоєний матеріал; ввести поняття “конкурентоспроможних відрізків”; ознайомити з теоремою Нагеля;
розвивальна: розвивати уміння використовувати сформовані знання, навички і уміння у нових ситуаціях; пробуджувати інтерес до історії математики;
виховна: прививати бажання мати якісні глибокі знання; виховувати зібраність, увагу, відповідальність і вимогливість до себе.
Обладнання: інформаційно-комунікативні засоби для показу запланованих рисунків.
Методика введення теми
- Перевірка домашнього завдання
- Вступ
Учитель: крилату фразу літературного персонажа Козьми Пруткова, що “ніхто не обійме неосяжного”, повною мірою можна віднести до геометрії трикутника. Насправді, “світ трикутників”, як криниця прекрасних і вражаючих геометричних конструкцій, невичерпний. Їх неосяжність і багатогранність, що ледве піддаються якій-небудь систематизації, не можуть не захоплювати. Утім, іншим разом ці благородні відчуття переростають у здивоване роздратування, майже в протест: якщо вже з вигляду така «іграшкова» область геометрії настільки складна, то в чому ж тоді взагалі можна розібратися?
Минулого разу ми познайомилися з Дж. Чеви, його теоремою та теоремою Жергонна. Розглянули задачі на застосування цих теорем, але це не все! Сьогодні ми розглянемо теорему Нагеля, яка пов’язана з умовою Чеви.
|
|
- Засвоєння
![]() Теорема Нагеля: якщо точки X, Y, Z є точками дотику зовнівписаних кіл трикутника, то відрізки AX, BY і CZ перетинаються в одній точці N, точці Нагеля (рис.53).
Теорема Нагеля: якщо точки X, Y, Z є точками дотику зовнівписаних кіл трикутника, то відрізки AX, BY і CZ перетинаються в одній точці N, точці Нагеля (рис.53).
Доведення: необхідно довести, що виконується умова Чеви.
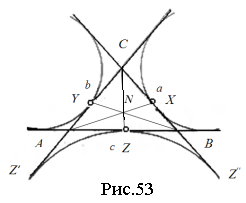 Розглянемо відрізки AZ і AZ′, де точка Z′ є точкою дотику сторони АС трикутника АВС до зовнівписаного кола з центром Ос. Вони рівні (чому?). Так само
Розглянемо відрізки AZ і AZ′, де точка Z′ є точкою дотику сторони АС трикутника АВС до зовнівписаного кола з центром Ос. Вони рівні (чому?). Так само ![]() ,
, ![]() , де точка Z′′ є точкою дотику сторони ВС трикутника АВС до зовнівписаного кола з центром Оа. А
, де точка Z′′ є точкою дотику сторони ВС трикутника АВС до зовнівписаного кола з центром Оа. А ![]() (рис.53), тоді
(рис.53), тоді
![]() .
.
Тому
![]() ,
,![]() ,
,
![]() ,
,![]() , (*)
, (*)
![]() ,
,![]() .
.
Підставимо отримане в (1) і матимемо вірну тотожність [30, 11].
Звернемо увагу на співвідношення (*), отримані при доведенні попередньої теореми. Що це за відрізки ![]() ,
, ![]() ,
, ![]() ? Чим вони можуть нас зацікавити?
? Чим вони можуть нас зацікавити?
Як ми вже знаємо, існують “чудові точки”, “ чудові прямі” (з ними ми зустрінемося наступного разу і познайомимося більш детально). А “чудові відрізки”! Якось про відрізки як про чудове явище геометрії питання не з’являлось. Спробуємо довести, що ці три відрізки можуть скласти “конкуренцію” “чудовим прямим”. І назвемо їх конкурентоспроможними відрізками.
![]() Конкуренція 1. Кожну сторону трикутника можна уявити як суму двох конкурентоспроможних відрізків.
Конкуренція 1. Кожну сторону трикутника можна уявити як суму двох конкурентоспроможних відрізків.
Наприклад:
![]() .
.
 Хоча сума двох конкурентоспроможних відрізків постійна, їх спільна точка на стороні трикутника не одна й та ж сама.
Хоча сума двох конкурентоспроможних відрізків постійна, їх спільна точка на стороні трикутника не одна й та ж сама.
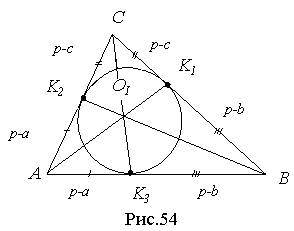
Розглянемо відрізки р - а, р - b, р - с. Якщо кінець конкурентоспроможного відрізка співпаде з відповідною від’ємнику вершиною (р-а з А, р-b з B, р-с з С), то спільною точкою двох відрізків буде точка дотику вписаного в трикутник кола (рис. 54) [21, 9].
![]()
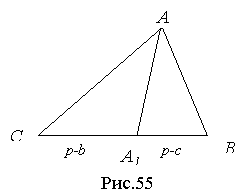 Конкуренція 2. Якщо кінець конкурентоспроможного відрізка не співпадає з відповідною від’ємнику вершиною (наприклад, р-b з В, р-c з С), то спільною точкою двох відрізків буде точка, яка поділяє периметр трикутника навпіл (рис.55). Цю точку будемо позначати відповідно вершині A1, B1 або C1.
Конкуренція 2. Якщо кінець конкурентоспроможного відрізка не співпадає з відповідною від’ємнику вершиною (наприклад, р-b з В, р-c з С), то спільною точкою двох відрізків буде точка, яка поділяє периметр трикутника навпіл (рис.55). Цю точку будемо позначати відповідно вершині A1, B1 або C1.
Є й інші способи побудови напівпериметричної точки.
![]() Другий спосіб. Щоб отримати точку А1, необхідно побудувати зовнівписане коло, до якого буде дотичною сторона ВС.
Другий спосіб. Щоб отримати точку А1, необхідно побудувати зовнівписане коло, до якого буде дотичною сторона ВС.
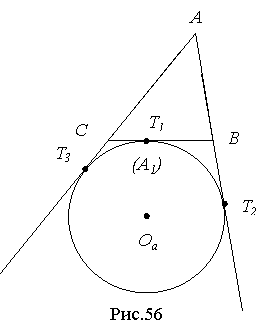 Доведення. Нехай зовні вписане коло з центром Oа дотикається продовжень сторін трикутника АВС в точках Т2 і Т3, а сторони ВС в точці Т1 (рис.56).
Доведення. Нехай зовні вписане коло з центром Oа дотикається продовжень сторін трикутника АВС в точках Т2 і Т3, а сторони ВС в точці Т1 (рис.56).
Позначимо СТ1=x, T1B=y. Тоді АТ2=с+y, АТ3=b+x і
2p = a + b + c = x + y + b + c = b + x + c + y = AT2 + AT3. Але АТ3 = АТ2, тоді 2АТ2 = 2р, звідки
АТ2 = АТ3 = р, (**)
СТ1 = р – b і T1B =р – с,
оскільки СТ1 = СТ3, то АС+СТ1 = р, а тому, Т1 – напівпериметрична точка, яка співпадає з точкою А1.
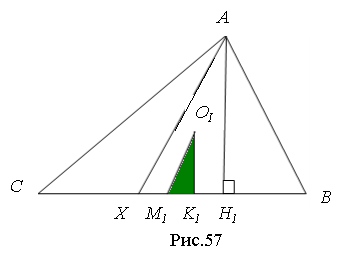
![]() Третій спосіб (конкурентна теорема). Якщо пряма АX (Х
Третій спосіб (конкурентна теорема). Якщо пряма АX (Х![]() ВС) паралельна відрізку ОIM1, то вона напівпериметрична пряма (ОI – інцентр (точка перетину бісектрис), М1 – середина ВС) (рис. 57).
ВС) паралельна відрізку ОIM1, то вона напівпериметрична пряма (ОI – інцентр (точка перетину бісектрис), М1 – середина ВС) (рис. 57).
Доведення. Позначимо BX=x, AH1 – висота трикутника АВС, ХН1=y, H1B=t. Знайдемо відрізок t з трикутників AH1В і AH1С користуючись теоремою Піфагора:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Трикутник ОIM1K1 подібний трикутнику AXH1 (за двома кутами: ![]() , за умовою теореми;
, за умовою теореми; ![]() , за побудовою), тоді
, за побудовою), тоді ![]() . Враховуючи, що
. Враховуючи, що ![]() (М1В =
(М1В = ![]() – за умовою; K1B = p-b – за конкуренцією 1; М1К1 = М1В - K1B ), маємо
– за умовою; K1B = p-b – за конкуренцією 1; М1К1 = М1В - K1B ), маємо ![]() (AH1 =
(AH1 = ![]() – висота; ОIK1 = r =
– висота; ОIK1 = r =![]() ).
).
![]() , BX=x=t+y,
, BX=x=t+y, ![]()
![]() , що і необхідно було довести [21, 9]
, що і необхідно було довести [21, 9]
Формули (*) і (**) часто застосовуються при розв’язуванні планіметричних задач, тому їх корисно запам’ятати.
- Застосування
Пригадаємо, що такі конкурентні відрізки використовуються у формулі Герона ![]() . Тому доречно довести останню формулу, користуючись формулами (*) і (**).
. Тому доречно довести останню формулу, користуючись формулами (*) і (**).
|
|
Доведення формули Герона. Проведемо в трикутнику АВС дотичну MN до вписаного кола, паралельно стороні АВ (рис.59). Трикутник AON прямокутний, оскільки ![]() , при цьому ОК = r ― висота, проведена з вершини прямого кута. Звідси,
, при цьому ОК = r ― висота, проведена з вершини прямого кута. Звідси, 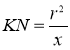 . Аналогічно з прямокутного трикутника BOM матимемо, що
. Аналогічно з прямокутного трикутника BOM матимемо, що 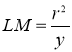 . Тоді,
. Тоді, 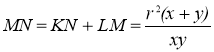 .
.
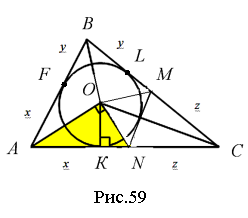 З формул (**) маємо, що z – напівпериметр трикутника MNC. У подібних трикутниках MNC і BAC напівпериметри відносяться як подібні сторони, тому p:z = AB:MN, тобто p:z = (x+y):
З формул (**) маємо, що z – напівпериметр трикутника MNC. У подібних трикутниках MNC і BAC напівпериметри відносяться як подібні сторони, тому p:z = AB:MN, тобто p:z = (x+y): 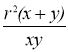 . Звідси p:z = xy:
. Звідси p:z = xy:![]() . Тому має місце рівність:
. Тому має місце рівність:
p![]() = xyz. (***)
= xyz. (***)
Легко побачити, що остання формула еквівалентна формулі Герона: оскільки ![]() , то з урахуванням формул (*) і (***) матимемо
, то з урахуванням формул (*) і (***) матимемо ![]() [6].
[6].
- Домашнє завдання
- Складіть і розв’яжіть задачу на використання однієї з розглянутих сьогодні конкуренцій, користуючись відомостями з попередніх уроків.
- Підготуйте емпатійний твір на тему “Найцікавіша чевіана трикутника” (можливе використання комп’ютерних програм).
Розділ III. Деякі чудові прямі трикутника
§3.1
Тема. Бісектриси.
Мета дидактична: навчити учнів застосовувати здобуті знання; креслити чіткі рисунки, досліджувати їх; виводити необхідні теореми;
розвивальна: розвивати пізнавальну активність учнів; формувати в учнів уміння працювати творчо; удосконалювати уміння аналізувати відповіді інших учнів і уміння виділяти головне;
виховна: виховувати культуру усної та письмової математичної мови, науковий світогляд, самостійність та ініціативність.
Обладнання: інформаційно-комунікаційні засоби для показу запланованих рисунків, схем.
Методика введення теми
І. Вступ
Ми вже з Вами обговорювали поняття “чудові прямі” трикутника та їх залежність від “чудових точок”. Представити її можна схематично (схема 1):
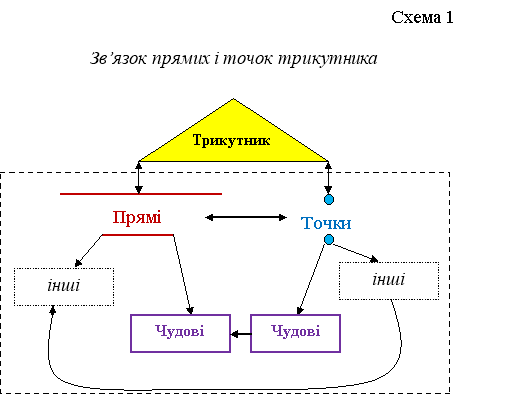
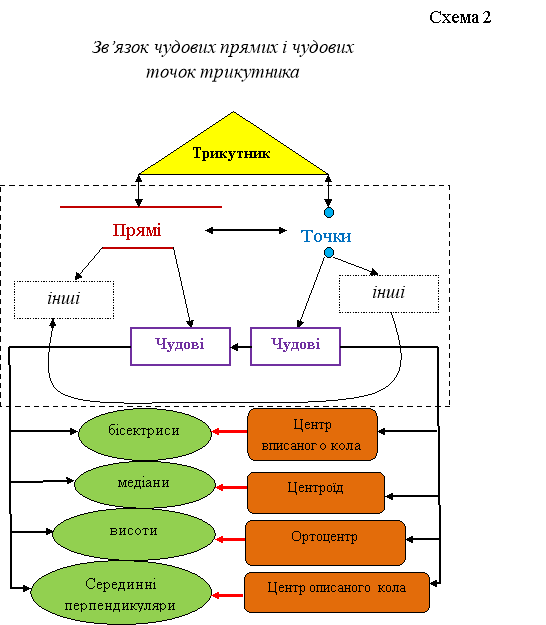 Згідно схеми, пряма трикутника буде чудовою у випадку, якщо “сімейство” цих прямих у трикутнику при перетині утворить чудову точку. Наприклад, бісектриса є чудовою прямою, адже усі бісектриси трикутника у перетині утворюють чудову точку, а саме інцентр (центр вписаного кола). Назвіть відомі Вам чудові прямі. Відповідь поясніть. (Висота, медіана, серединний перпендикуляр тощо.) Тепер ми можемо доповнити нашу схему (схема 2):
Згідно схеми, пряма трикутника буде чудовою у випадку, якщо “сімейство” цих прямих у трикутнику при перетині утворить чудову точку. Наприклад, бісектриса є чудовою прямою, адже усі бісектриси трикутника у перетині утворюють чудову точку, а саме інцентр (центр вписаного кола). Назвіть відомі Вам чудові прямі. Відповідь поясніть. (Висота, медіана, серединний перпендикуляр тощо.) Тепер ми можемо доповнити нашу схему (схема 2):
На сьогодні Ви приготували емпатійні твори про ці чудові прямі та авторські задачі. (Бажаючі читають свої твори.)
Наприклад: “Я бісектриса”.
 Учень: перш ніж я розкажу про себе, свою вагомість – відгадайте хто я, користуючись ребусом (рис.60).
Учень: перш ніж я розкажу про себе, свою вагомість – відгадайте хто я, користуючись ребусом (рис.60).
Отже, я – бісектриса. Моя назва у перекладі з латинської мови bis – “двічі” і seco – “розсікаю”.
Дуже часто мені дають “жартівливе означення”: “Бісектриса – це криса, яка бігає по кутам і ділить їх навпіл (рис.61)”.
 Щоб побачити, чим я корисна, розв’яжіть задачу.
Щоб побачити, чим я корисна, розв’яжіть задачу.
Задача. Перед Вами частина карти острова, на якому колись пірати зарили скарби (рис.62). На жаль, на карті не відмічене місце, де вони заховані, але збереглись орієнтири (камінь на розвилці доріг і три дуба) [16, 58]. Відомо, що скарби зариті у місці, однаково віддаленому від дубів і, одночасно, від двох доріг [16, 58]. За якої умови, користуючись даним орієнтиром, Ви зможете віднайти скарб?
 Відповідь. Скарби зариті у місці перетину бісектрис кутів, утворених дубами, за умови, що це місце знаходиться на бісектрисі кута, утвореного дорогами (рис.63).
Відповідь. Скарби зариті у місці перетину бісектрис кутів, утворених дубами, за умови, що це місце знаходиться на бісектрисі кута, утвореного дорогами (рис.63).
Учитель: cьогодні ми присвятимо наше заняття саме бісектрисам трикутника.
Давайте згадаємо математичне означення цьому поняттю:
Бісектрисами називають закріплені всередині трикутника відрізки прямих (чевіан), які ділять навпіл його кути. |
На рис.64 показана одна така бісектриса AL.
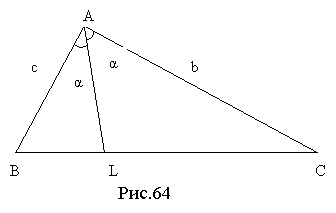
II. Засвоєння
Давайте, застосуємо теорему синусів до трикутників ABL і ALC (кути яких в точці L, являючись доповнювальними, мають рівні синуси). Будемо мати:
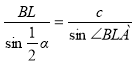 ,
, 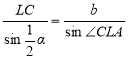
sin![]() BLA = sin
BLA = sin![]() CLA,
CLA,
тоді, ![]() . Аналогічний результат можна отримати для бісектрис кутів В і С. Таким чином, нами доведена теорема.
. Аналогічний результат можна отримати для бісектрис кутів В і С. Таким чином, нами доведена теорема.
Теорема 3.1.1.
![]() Бісектриса внутрішнього кута трикутника поділяє протилежну сторону на відрізки, довжини яких пропорційні довжинам прилеглих сторін [11, 19]. (Обернена теорема теж вірна.)
Бісектриса внутрішнього кута трикутника поділяє протилежну сторону на відрізки, довжини яких пропорційні довжинам прилеглих сторін [11, 19]. (Обернена теорема теж вірна.)
Наслідок:
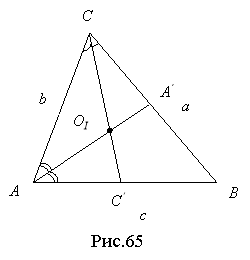
![]() Кожна бісектриса внутрішнього кута трикутника, точкою перетину, ділиться (рахуючи від вершини кута) у відношенні, яке відповідає відношенню суми прилеглих сторін до протилежної ( рис.65).
Кожна бісектриса внутрішнього кута трикутника, точкою перетину, ділиться (рахуючи від вершини кута) у відношенні, яке відповідає відношенню суми прилеглих сторін до протилежної ( рис.65).
![]()
Доведення: За теоремою 3.1.1.:
![]()
![]() =
= ![]() .
.
Виділимо наступні властивості бісектрис трикутника:
-
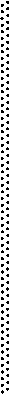 У довільному трикутнику ABC має місце залежність
У довільному трикутнику ABC має місце залежність 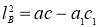 , де lB – довжина бісектриси кута В; а, с – довжини сторін ВС і ВА відповідно; а1,с1 – довжини відрізків, на які бісектриса кута В поділяє сторону АС, прилеглих до сторін ВС і ВА відповідно (рис.67). Цю рівність називають формулою Лагранжа [3, 125].
, де lB – довжина бісектриси кута В; а, с – довжини сторін ВС і ВА відповідно; а1,с1 – довжини відрізків, на які бісектриса кута В поділяє сторону АС, прилеглих до сторін ВС і ВА відповідно (рис.67). Цю рівність називають формулою Лагранжа [3, 125].
-
У довільному трикутнику ABC довжина lB бісектриси кута В виражається формулою
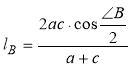 (рис.67) [11, 24].
(рис.67) [11, 24].
- Якщо у трикутнику АВС АА1 і СС1 – бісектриси, які перетинаються в точці Е (рис.68), то має місце рівність
![]() [11, 27].
[11, 27].
|
“Лагранж – найвеличніша піраміда наук”, – так оцінив Наполеон Бонапарт видатного вченого і найскромнішого математика XVIII ст. Жозефа Луї Лагранжа (1736 – 1813рр.), якого він зробив сенатором, графом імперії і командором ордена Почесного легіону (рис.66). У 14 років Лагранж уже мав наукові роботи, а у 19 – став професором математики.
Його останні слова: “Я зробив свою справу: досяг деяких успіхів у математиці. Я ніколи не відчував ненависті, не робив нічого поганого…” |
Тепер наше завдання: довести ці властивості і розглянути приклади їх застосування.
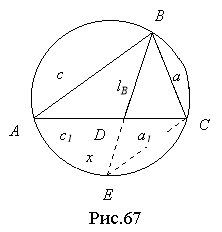 Доведення властивості 1. Навколо трикутника АВС опишемо коло і продовжимо бісектрису BD кута В до перетину з колом у точці Е (рис.67). З’єднаємо точки Е та С. Позначимо, DE = x. Кути ВАС і ВЕС спираються на одну дугу ВС, тому вони рівні.
Доведення властивості 1. Навколо трикутника АВС опишемо коло і продовжимо бісектрису BD кута В до перетину з колом у точці Е (рис.67). З’єднаємо точки Е та С. Позначимо, DE = x. Кути ВАС і ВЕС спираються на одну дугу ВС, тому вони рівні.
У трикутниках ВАD і ВЕС ![]() ,
, ![]() . Тоді трикутники ВАD і ВЕС подібні, і
. Тоді трикутники ВАD і ВЕС подібні, і 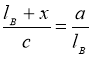 .
.
З останньої рівності маємо ![]() . А оскільки трикутники BAD і CЕD подібні, то
. А оскільки трикутники BAD і CЕD подібні, то ![]() . Тоді
. Тоді ![]() .
.
Аналогічні вирази можна записати для lc і la.
Доведення властивості 2. Нехай бісектриса кута В перетинає сторону АС в точці D (рис.67). Очевидно, що ![]() або
або
![]() .
.
Поділивши обидві частини останнього рівняння на ![]() , одержимо:
, одержимо:
![]() , звідки
, звідки 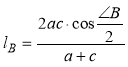 .
.
Аналогічні формули можна вивести для бісектрис lc і la.
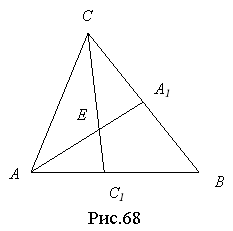 Доведення властивості 3. Розглянемо трикутник АЕС (рис.68). У ньому
Доведення властивості 3. Розглянемо трикутник АЕС (рис.68). У ньому
![]() .
.
Тоді ![]() .
.
Але ![]() .
.
Тому, ![]() .
.
III. Застосування
Задача 3.1.1. Знайдіть бісектрису кута В трикутника АВС і визначте у якому відношенні центр вписаного у трикутник кола поділяє цю бісектрису, якщо AB = 4, BC = 5 і AC = 6.
Задача 3.1.2. У трикутнику АВС кут А вдвічі більший за кут В, а довжини сторін, що лежать навпроти цих кутів, відповідно дорівнюють 12 см і 8 см. Знайдіть довжину третьої сторони трикутника [11, 22].
Задача 3.1.3. У трикутнику АВС виконується співвідношення
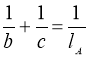 ,
,
де b, c ― довжини сторін трикутника, а lA ― довжина бісектриси кута, утвореного цими сторонами. Знайдіть величину кута між даними сторонами [11, 25].
Задача 3.1.4. Задано дві сторони трикутника a, b і кут ![]() між ними. Знайдіть радіус кола, що проходить через кінці третьої сторони і центр вписаного в цей трикутник кола [11, 28].
між ними. Знайдіть радіус кола, що проходить через кінці третьої сторони і центр вписаного в цей трикутник кола [11, 28].
![]() IV. Домашнє завдання
IV. Домашнє завдання
Задача 3.1.5. Задано дві сторони трикутника a, b і довжина l бісектриси кута між ними. Знайдіть третю сторону трикутника [11, 23].
Задача 3.1.6. У трикутнику KLM проведені бісектриси KN і LP, що перетинаються у точці Q (рис.). Відрізок PN має довжину 1 м і вершина М лежить на колі, що проходить через точки P, Q і N. Знайдіть кути трикутника PQN [11, 28].
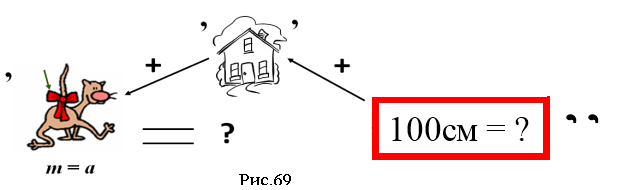 Задача 3.1.7. Розв’яжіть ребус (рис.69). Тим самим Ви дізнаєтесь ключове слово теми нашого наступного заняття.
Задача 3.1.7. Розв’яжіть ребус (рис.69). Тим самим Ви дізнаєтесь ключове слово теми нашого наступного заняття.
§3.2
Тема. Медіани та серединний трикутник.
Мета дидактична: розширити та поглибити знання учнів з теми “Медіани та серединний трикутник”; навчити їх застосовувати здобуті знання;
розвивальна: розвивати пізнавальну активність учнів; формувати в учнів уміння працювати творчо;
виховна: виховувати культуру усної та письмової математичної мови, науковий світогляд, самостійність та ініціативність.
Обладнання: інформаційно-комунікаційні засоби для показу запланованих рисунків, властивостей медіан.
Методика введення теми
- Перевірка домашнього завдання
- Мотивація
Учитель. Хто виконав домашнє завдання, знають, що ключове слово теми сьогоднішнього уроку – медіана. Медіана у перекладі з латинської мови mediana – “середня”. Давайте згадаємо означення медіан трикутника:
|
|
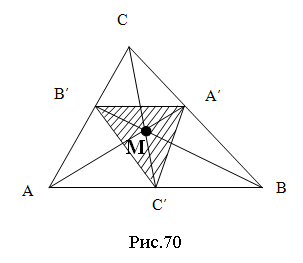
Якщо з’єднати між собою основи медіан (середини сторін трикутника), то отримаємо серединний трикутник (∆В̕А̕С̕) або його ще називають додатковим трикутником (рис.70) [14, 18].
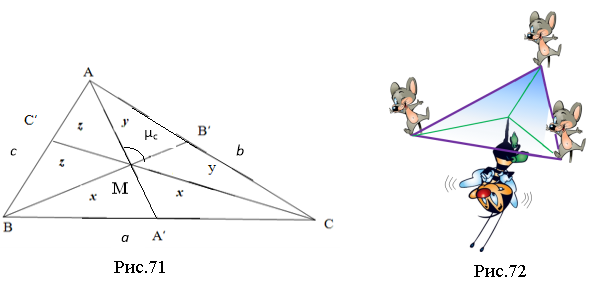 Яку з властивостей медіан Ви вже знаєте? (Згідно теореми Чеви, медіани перетинаються в одній точці. Ця точка (М) має назву – центроїд, центр мас або барицентр (рис.71).)
Яку з властивостей медіан Ви вже знаєте? (Згідно теореми Чеви, медіани перетинаються в одній точці. Ця точка (М) має назву – центроїд, центр мас або барицентр (рис.71).)
 Чим можна пояснити такі назви утвореної точки? Справа в тому, що якщо однорідну трикутну пластинку поставити на шпильку таким чином, щоб вістря останньої потрапило точно в центроїд, то пластинка буде знаходитись у рівновазі (рис.72). Цікаво те, що центр мас дротяного трикутного контуру співпадає з іншою точкою – з центром вписаного кола його серединного трикутника [52, 284]. (Вдома практично перевірте цей факт.)
Чим можна пояснити такі назви утвореної точки? Справа в тому, що якщо однорідну трикутну пластинку поставити на шпильку таким чином, щоб вістря останньої потрапило точно в центроїд, то пластинка буде знаходитись у рівновазі (рис.72). Цікаво те, що центр мас дротяного трикутного контуру співпадає з іншою точкою – з центром вписаного кола його серединного трикутника [52, 284]. (Вдома практично перевірте цей факт.)
Давайте детальніше розглянемо рис. 71.
S∆МBA̕ = S∆МA̕C, оскільки ці трикутники мають рівновеликі основи і спільну висоту. Позначимо ці площі через x.
З тих же міркувань, маємо:
S∆МCB̕ = S∆МB̕A і S∆МAC̕ = S∆МC̕B.
Ці площі позначимо через y і z відповідно.
Також маємо, що S∆CAC̕ = S∆CC̕B, тобто 2y + z = z + 2x , звідси, x = y . Аналогічно, S∆ABA̕ = S ∆AA̕C , звідси, y = z . Отже, ми показали, що x = y = z, і тим самим довели теорему 3.2.1.
ІІІ. Засвоєння
![]() Теорема 3.2.1 Медіани трикутника поділяють його на шість рівновеликих трикутників.
Теорема 3.2.1 Медіани трикутника поділяють його на шість рівновеликих трикутників.
Розглядаємо рис.71 далі. Зазначимо, що S∆МAB = 2S∆МBA̕. Оскільки ці трикутники мають спільну висоту, то AМ = 2МA̕. Аналогічно, BМ = 2МB' і СМ = 2МС', тобто має місце теорема 3.2.2.:
![]() Теорема 3.2.2. Точка перетину медіан ділить їх у відношенні 2:1, рахуючи від вершин.
Теорема 3.2.2. Точка перетину медіан ділить їх у відношенні 2:1, рахуючи від вершин.
Бажаючим розглянути інші доведення цієї теореми необхідно звернутися до [13].
![]() Розглянемо ще деякі властивості медіан:
Розглянемо ще деякі властивості медіан:
|
S∆ABC = |
-
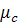 – це кут між медіанами, що не проведені до сторони с.
– це кут між медіанами, що не проведені до сторони с.
|
|
2. .
|
S∆ABC = |
3.
|
|
4.
|
|
![]() 5..
5..
Властивостями 1 і 3 можна доповнити таблицю 2 (Додаток Б).
Доведення 1. (див. рис. 71) Як вже відомо, S∆A̕МB = ![]() а S∆A̕МB =
а S∆A̕МB = 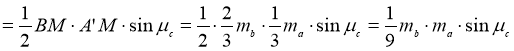 .
.
Отже, S∆ABC = 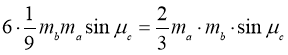 .
.
Доведення 2. Користуючись властивістю 1, запишемо:
S∆ABC =![]() .
.
Отже,
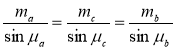
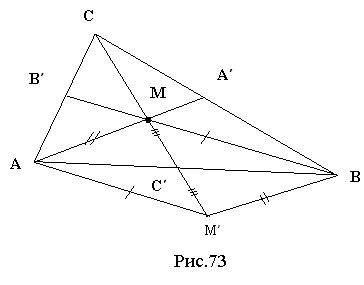
Доведення 3. AМBМ̕ – паралелограм (рис.73).
Розглянемо ∆BММ̕:
МB = ![]()
![]() , М̕B =
, М̕B = ![]() , ММ̕ =
, ММ̕ = ![]() (за теоремою 3.2.2).
(за теоремою 3.2.2).
 Тоді,
Тоді,
S∆BММ̕ =![]() S∆ABC =
S∆ABC = ![]() S∆ABC.
S∆ABC.
Позначимо через
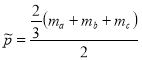 ,
,
і підставимо у формулу Герона:
S∆ABC = 3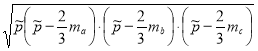 .
.
Після зведення подібних, отримаємо необхідне.
Доведення 4. Користуючись рисунком 73, запишемо:
![]() =
= ![]() ,
, ![]() =
= ![]() .
.
Тоді, з ∆М̕BМ:
![]() .
.
Звідси,
![]() .
.
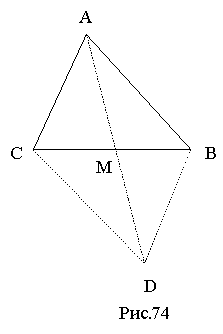 Доведення 5. Добудуємо трикутник АВС, у якому АМ – медіана, до паралелограма (рис.74). Тоді кут
Доведення 5. Добудуємо трикутник АВС, у якому АМ – медіана, до паралелограма (рис.74). Тоді кут ![]() і МD = ma. Застосуємо теорему косинусів до ∆ABD і ∆ABC.
і МD = ma. Застосуємо теорему косинусів до ∆ABD і ∆ABC.
Тоді ![]() і
і ![]() .
.
Якщо скласти ці рівності, то матимемо ![]() або
або 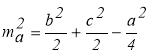 , що й необхідно було довести.
, що й необхідно було довести.
Аналогічно доводяться інші співвідношення [11, 30].
Також зазначимо, що для серединного трикутника (рис.70) (перевірити самостійно):
|
S∆A̕B̕C̕ = |
1.
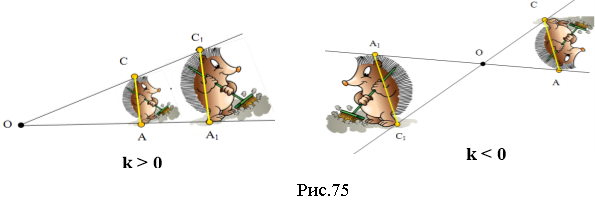
2. ∆A̕B̕C̕ – гомотетичний ∆ABC, якщо центр гомотетії – центроїд (точка М), то ![]() – коефіцієнт гомотетії.
– коефіцієнт гомотетії.
Пригадаємо, що таке гомотетія.
|
|
ІV. Застосування
Задача 3.2.1. Медіани трикутника дорівнюють 5см, ![]() см і
см і ![]() см. Доведіть, що трикутник прямокутний [11, 30].
см. Доведіть, що трикутник прямокутний [11, 30].
Задача 3.2.2. Визначіть сторони трикутника, якщо його медіани дорівнюють ![]() ,
, ![]() і
і ![]() .
.
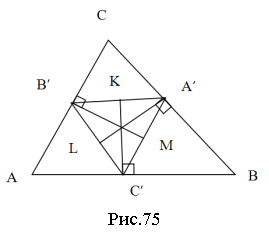
Задача 3.2.3. У трикутнику АВС (рис.75) В̕М, А̕L, С̕К – серединні перпендикуляри. Їх лінійні виміри відповідно 3, 4 і 5. Знайдіть площу трикутника АВС.
![]() IV. Домашнє завдання
IV. Домашнє завдання
Задача 3.2.4. Виразіть довжину медіани AA̕ (рис. 71) через a,b,c, користуючись теоремою Стюарта (див. задачу 2.1.1).
Задача 3.2.5. У трикутнику АВС, АВ = 8, ВС = 14 і АС = 18, проведено медіану ВМ, що поділяється точкою Е у відношенні ВЕ : EM = 8 : 9. Знайдіть відстань від точки Е до вершини А [11, 31].
Задача 3.2.6. Приховане у ребусі слово – це “перепустка” на наступне заняття.

§3.3
Тема: Висоти та ортотрикутник.
Мета дидактична: розширити та поглибити знання учнів з теми “Висоти та ортотрикутник ”;
розвивальна: розвивати пізнавальну активність учнів; формувати в учнів уміння працювати творчо, уміння вбачати красу тверджень, формул, гіпотез, доведень тощо; сприяти глибокому та активному засвоєнню знань через естетичне сприйняття навчального матеріалу;
виховна: виховувати культуру усної та письмової математичної мови, науковий світогляд, самостійність та ініціативність.
Обладнання: інформаційно-комунікаційні засоби для показу запланованих рисунків.
Методика введення теми
- Перевірка домашнього завдання
- Вступ
Учитель: на минулих заняттях ми з Вами розглядали бісектриси, медіани, їх місце і роль у трикутнику. Сьогодні ми присвятимо наше заняття, як Ви вже здогадалися, висотам трикутника. Спочатку пригадайте означення цього поняття, а потім – запитання “на засипку”.
Означення можна сформулювати у такому вигляді:
|
|
Запитання: як Ви гадаєте, якщо провести бісектрису, медіану і висоту з однієї вершини у довільному трикутнику, то яким буде їх взаємне розташування?
Відповідь запишемо, як теорему 3.3.1.
![]() Теорема 3.3.1. У нерівнобедреному трикутнику бісектриса завжди міститься між його висотою і медіаною, проведеними з тієї самої вершини [3, 29].
Теорема 3.3.1. У нерівнобедреному трикутнику бісектриса завжди міститься між його висотою і медіаною, проведеними з тієї самої вершини [3, 29].
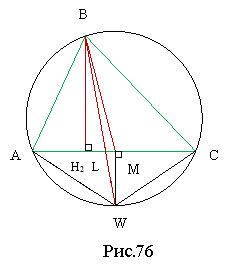
Доведення. Нехай продовження бісектриси lB трикутника АВС перетинає коло, описане навколо цього трикутника, у точці W (рис.76). Відрізок BW перетинає АС у точці L. Проекції його кінців на пряму АС є основою висоти hB і точкою М відрізка АС. Покажемо, що точка М є серединою відрізка АС. Для цього розглянемо такі кути:
![]() CBW =
CBW = ![]() CAW =
CAW = ![]()
![]() АBС, як вписані, що спираються на дугу WC;
АBС, як вписані, що спираються на дугу WC;
![]() ABW =
ABW = ![]() ACW =
ACW = ![]()
![]() АBС, як вписані, що спираються на спільну дугу AW.
АBС, як вписані, що спираються на спільну дугу AW.
Тоді ![]() CAW =
CAW = ![]() ACW =
ACW = ![]()
![]() АBС. Звідси, трикутник АWC – рівнобедрений і WМ у трикутнику АWC буде медіаною, а точка М – серединою відрізка АС.
АBС. Звідси, трикутник АWC – рівнобедрений і WМ у трикутнику АWC буде медіаною, а точка М – серединою відрізка АС.
Оскільки точки В і W лежать у різних півплощинах відносно прямої АС, то точка L буде внутрішньою точкою відрізка HM. Теорема доведена.
Тепер, коли ми з’ясували взаємне розміщення бісектриси, медіани і висоти, проведених з тієї самої вершини, повернемось до теми заняття. Що ще Ви знаєте про висоти трикутника? (Перетинаються в одній точці за теоремою Чеви.)
Розглянемо наступне означення:
|
|
Ортоцентр має незвичайні та цікаві властивості. Ця точка досліджується вже протягом багатьох століть. За цей час вона стала однією з найважливіших точок у геометрії трикутника. Тож давайте напнемо вітрила нашого корабля і вирушимо назустріч труднощам, здивуванням і новим відкриттям!
ІIІ. Засвоєння
![]() Властивості ортоцентра:
Властивості ортоцентра:
1. Точки, симетричні ортоцентру відносно сторін трикутника, належать описаному навколо трикутника колу (рис. 77).
2. Відрізки АН і АО (т.О – центр описаного кола) утворюють рівні кути з бічними сторонами трикутника (ри.78).
3. Кожну з точок А, В, С, Н (де А, В, С — вершини трикутника АВС, а Н – ортоцентр цього трикутника) можна розглядати як ортоцентр трикутника, утвореного трьома іншими.
4. Якщо три чевіани, проведені з вершин трикутника АВС, перетнулися в одній точці і утворили рівні кути так, як показано на рис. 79, то ці три чевіани є висотами, а точка їх перетину співпадає з ортоцентром трикутника АВС.
![]() 5. Якщо коло, описане навколо трикутника АВС, дзеркально відобразити відносно сторін трикутника, то здобуті три кола перетнуться в ортоцентрі трикутника (рис. 80) [12, 16].
5. Якщо коло, описане навколо трикутника АВС, дзеркально відобразити відносно сторін трикутника, то здобуті три кола перетнуться в ортоцентрі трикутника (рис. 80) [12, 16].
Доведення 1. Позначимо точку D, симетричну ортоцентру відносно сторони a (рис.77). ![]() H2HH3 = 180o –
H2HH3 = 180o – ![]() A (з чотирикутника AH2HH3, 360о –
A (з чотирикутника AH2HH3, 360о – ![]() AH2H –
AH2H – ![]() AH3H –
AH3H – ![]() BAC = 360o – 90o – 90o –
BAC = 360o – 90o – 90o – ![]() A).
A). ![]() BHC =
BHC = ![]() H2HH3 = 180˚ –
H2HH3 = 180˚ – ![]() A (вертикальні). ∆ВНС = ∆BDC (згідно симетрії). Звідси маємо, що
A (вертикальні). ∆ВНС = ∆BDC (згідно симетрії). Звідси маємо, що ![]() BDC = 180˚ –
BDC = 180˚ – ![]() A. Оскільки сума протилежних кутів чотирикутника ABDC дорівнює 180˚ (
A. Оскільки сума протилежних кутів чотирикутника ABDC дорівнює 180˚ (![]() BAC +
BAC + ![]() BDC = 180˚ –
BDC = 180˚ – ![]() A +
A + ![]() A = 180˚), то цей чотирикутник є вписаним в деяке коло, а це рівнозначно тому, що точка D належить описаному навколо трикутника ABC колу, що й треба було довести.
A = 180˚), то цей чотирикутник є вписаним в деяке коло, а це рівнозначно тому, що точка D належить описаному навколо трикутника ABC колу, що й треба було довести.
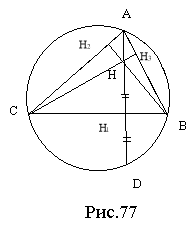 Аналогічно доводиться ця властивість для двох інших сторін.
Аналогічно доводиться ця властивість для двох інших сторін.
Зауважимо, що у випадку, коли трикутник ABC буде тупокутним, ця властивість зберігається, незважаючи на те, що ортоцентр розташований за межами трикутника. Доведіть цей факт самостійно.
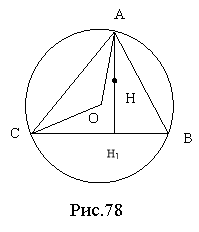 Доведення 2. Користуючись рис.78,
Доведення 2. Користуючись рис.78, ![]() ВАН1 = 90˚ –
ВАН1 = 90˚ – ![]() В (з трикутника АВН1).
В (з трикутника АВН1). ![]() АОС = 2
АОС = 2![]() В (чому?). Оскільки трикутник АОС рівнобедрений (АО = ОС – радіус описаного кола), то
В (чому?). Оскільки трикутник АОС рівнобедрений (АО = ОС – радіус описаного кола), то ![]() САО =
САО = 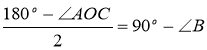 . Звідси маємо, що
. Звідси маємо, що ![]() САО =
САО = ![]() ВАН1, що й треба було довести.
ВАН1, що й треба було довести.
Доведення 3. Необхідно розглянути такі випадки (рис.77):
∆АВС з ортоцентром Н (1);
∆ВНС з ортоцентром А (2);
∆АНВ з ортоцентром С (3);
∆ АНС з ортоцентром В (4).
(1): ![]() ,
, ![]() ,
, ![]() , АH1, ВH2, СH3 перетинаються в одній точці H. Доведено.
, АH1, ВH2, СH3 перетинаються в одній точці H. Доведено.
(2): BH2 – продовження сторони BH, CH3 – продовження сторони СH, BH3 – висота на CH, CH2 – висота на BH, HH1 – висота на BC. Доведено.
Самостійно розібратися з (3) і (4).
Доведення 4. Нехай X — точка перетину чевіан; ![]() — основи чевіан, проведених відповідно до сторін a,b,с трикутника АВС (рис.79). Позначимо рівні кути через α, φ та β (відповідно до кількості дужок). Оскільки сума кутів трикутника дорівнює 180˚, то 2α + 2β + 2φ = 180˚. Звідси маємо, що α + β + φ = 90˚
— основи чевіан, проведених відповідно до сторін a,b,с трикутника АВС (рис.79). Позначимо рівні кути через α, φ та β (відповідно до кількості дужок). Оскільки сума кутів трикутника дорівнює 180˚, то 2α + 2β + 2φ = 180˚. Звідси маємо, що α + β + φ = 90˚
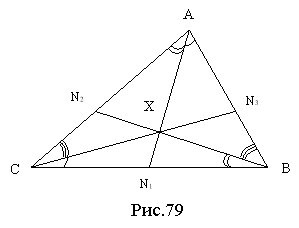 Тепер розглянемо трикутник
Тепер розглянемо трикутник ![]()
![]() :
:
![]()
Отже, ![]() — висота, проведена до сторони а трикутника АВС. Аналогічно доводиться, що
— висота, проведена до сторони а трикутника АВС. Аналогічно доводиться, що ![]() , та
, та ![]() — теж висоти. Отже, точка їх перетину – точка Х – співпадає з ортоцентром трикутника АВС.
— теж висоти. Отже, точка їх перетину – точка Х – співпадає з ортоцентром трикутника АВС.
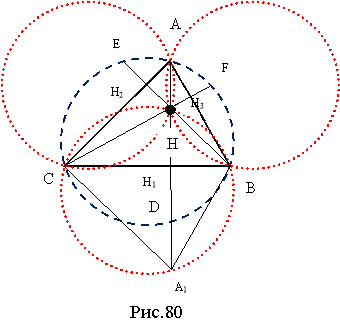 Доведення 5. Нехай D, Е, F — точки, симетричні ортоцентру відносно сторін а, b, с (рис.80). Доведемо, що коло, дзеркально відображене відносно сторони а, пройде через ортоцентр трикутника АВС – точку Н. Знаючи, що точка D, симетрична ортоцентру відносно сторони а, належить і описаному навколо трикутника АВС колу (за властивістю №1), ми можемо з упевненістю сказати, що точка D буде ортоцентром трикутника, дзеркально відображеного відносно сторони а (на рисунку – трикутника
Доведення 5. Нехай D, Е, F — точки, симетричні ортоцентру відносно сторін а, b, с (рис.80). Доведемо, що коло, дзеркально відображене відносно сторони а, пройде через ортоцентр трикутника АВС – точку Н. Знаючи, що точка D, симетрична ортоцентру відносно сторони а, належить і описаному навколо трикутника АВС колу (за властивістю №1), ми можемо з упевненістю сказати, що точка D буде ортоцентром трикутника, дзеркально відображеного відносно сторони а (на рисунку – трикутника ![]() ). А точка Н буде для цього трикутника точкою, симетричною ортоцентру D відносно його сторони ВС, і, отже, коло, описане навколо трикутника
). А точка Н буде для цього трикутника точкою, симетричною ортоцентру D відносно його сторони ВС, і, отже, коло, описане навколо трикутника ![]() ВС, пройде через точку Н.
ВС, пройде через точку Н.
Аналогічно доводиться, що два інших кола також пройдуть через точку Н.
Отже, оскільки ми довели, що всі три кола, дзеркально відображені відносно сторін трикутника АВС, пройдуть через точку Н, то вони дійсно перетинаються в точці Н. Властивість доведено.
Окрім того, що з висотами пов’язаний ортоцентр, вони слугують фундаментом для поняття ортотрикутник.
|
|
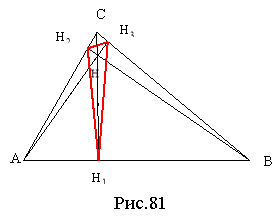
Ортотрикутник можна зустріти у графіці “Порядок и хаос” талановитого білоруського математика Ігара Жука (1950 – 2002 рр.) (рис.82).
Що, на Вашу думку намагався донести своєю картиною І. Жук? Що саме він відносить до “порядку”, а що до “хаосу”?

Для кращого осмислення зображеного (учитель вказує на графіку), ознайомимося з поняттям ортотрикутник, його властивостями і застосуванням детальніше.
Повернемося до рисунка 81. Розглянемо трикутники АНН1 і СНН3. Які вони між собою? (Подібні.) Чому?
Тоді
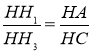 ,
,
і АН∙НН3 = НН1∙СН. Аналогічно, для трикутників АH2H і ВН3Н
АН∙НН3 = ВН∙НH2
Тому має місце рівність для трикутника АВС:
|
АН∙НН3 = ВН∙НН2 = СН∙НН1 |
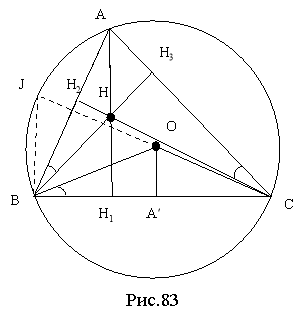 Можна багато дізнатись, досліджуючи рис. 83. Пояснимо, чому позначено декілька кутів на рисунку однією кількістю дуг, що мають значення 90˚ –
Можна багато дізнатись, досліджуючи рис. 83. Пояснимо, чому позначено декілька кутів на рисунку однією кількістю дуг, що мають значення 90˚ – ![]() А. По-перше, трикутник ОА̕С подібен трикутнику JBC (Чому?). Тоді
А. По-перше, трикутник ОА̕С подібен трикутнику JBC (Чому?). Тоді ![]() А̕ОС =
А̕ОС = ![]() А (Чому?). Таким чином, величина кожного з кутів при основі рівнобедреного трикутника ОВС дорівнює 90˚ –
А (Чому?). Таким чином, величина кожного з кутів при основі рівнобедреного трикутника ОВС дорівнює 90˚ – ![]() А. З прямокутних трикутників АВН3 і АСН2 отримуємо ті ж самі значення для кутів
А. З прямокутних трикутників АВН3 і АСН2 отримуємо ті ж самі значення для кутів ![]() Н3ВА і
Н3ВА і ![]() АСН2.
АСН2.
Використовуючи чотирикутники ВН1НН2 і СН3НН1, які є вписаними (Чому?), знаходимо, що
![]() НН1Н2 =
НН1Н2 = ![]() НВН2 =
НВН2 = ![]() Н3ВН2 =
Н3ВН2 = ![]() Н3СН =
Н3СН = ![]() Н3Н1Н
Н3Н1Н
Таким чином, відрізок Н1Н є бісектрисою кута ![]() Н3Н1Н2. Із тих же міркувань отримуємо, що відрізок Н3Н поділяє навпіл кут
Н3Н1Н2. Із тих же міркувань отримуємо, що відрізок Н3Н поділяє навпіл кут ![]() Н2Н3Н1, а відрізок НН2 – кут
Н2Н3Н1, а відрізок НН2 – кут ![]() Н1Н2Н3. Тому ми можемо сформувати наступний, досить таки цікавий результат: висоти в трикутнику є бісектрисами його ортотрикутника. Цей результат можна сформулювати так:
Н1Н2Н3. Тому ми можемо сформувати наступний, досить таки цікавий результат: висоти в трикутнику є бісектрисами його ортотрикутника. Цей результат можна сформулювати так:
![]() Теорема 3.3.2: Ортоцентр гострокутного трикутника є центром кола, вписаного в його ортотрикутник [17, 28].
Теорема 3.3.2: Ортоцентр гострокутного трикутника є центром кола, вписаного в його ортотрикутник [17, 28].
Ми вже відмітили на рисунку 83, що ![]() НН1Н2 =
НН1Н2 = ![]() Н1ВО. А оскільки відрізок НН1 перпендикулярний відрізку Н1В, то відрізок Н2Н1 має бути перпендикулярний відрізку ОВ. Аналогічно можна відмітити, що перпендикулярні відрізки Н1Н2 і ОС, Н3Н2 і ОА.
Н1ВО. А оскільки відрізок НН1 перпендикулярний відрізку Н1В, то відрізок Н2Н1 має бути перпендикулярний відрізку ОВ. Аналогічно можна відмітити, що перпендикулярні відрізки Н1Н2 і ОС, Н3Н2 і ОА.
Далі звернемося до теореми Фаньяно, доведення якої було опубліковано у 1755р.
|
|

![]() Теорема Фаньяно. Серед усіх трикутників, вписаних у даний гострокутний трикутник, найменший периметр має ортотрикутник.
Теорема Фаньяно. Серед усіх трикутників, вписаних у даний гострокутний трикутник, найменший периметр має ортотрикутник.
 Цей результат можна пояснити за допомогою законів фізики. Згадаємо, що висоти трикутника є бісектрисами його ортотрикутника. Тому промінь світла, пущений уздовж однієї із сторін ортотрикутника відіб'ється послідовно від усіх сторін трикутника ABC і повернеться у початкову точку. Таким чином, контур ортотрикутника є замкнутою траєкторією променя світла, а, як відомо, світло поширюється по найкоротшому шляху. Якщо розмістити три дзеркала так, щоб вони утворили гострокутний трикутник, то промінь світла, що йтиме по сторонам ортотрикутника, замкнеться і ніколи не вийде назовні. Математики говорять, що сторони ортотрикутника утворюють більярд для даного трикутника (рис.85) [36, 6].
Цей результат можна пояснити за допомогою законів фізики. Згадаємо, що висоти трикутника є бісектрисами його ортотрикутника. Тому промінь світла, пущений уздовж однієї із сторін ортотрикутника відіб'ється послідовно від усіх сторін трикутника ABC і повернеться у початкову точку. Таким чином, контур ортотрикутника є замкнутою траєкторією променя світла, а, як відомо, світло поширюється по найкоротшому шляху. Якщо розмістити три дзеркала так, щоб вони утворили гострокутний трикутник, то промінь світла, що йтиме по сторонам ортотрикутника, замкнеться і ніколи не вийде назовні. Математики говорять, що сторони ортотрикутника утворюють більярд для даного трикутника (рис.85) [36, 6].
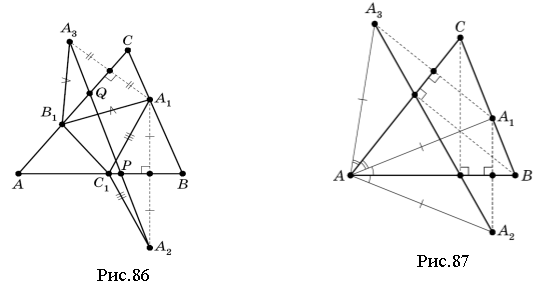 Доведення теореми Фаньяно. Нехай точки A1, B1, C1 лежать на сторонах трикутника ABC (A1 – на стороні BC і т. д.). Відобразимо точку A1 симетрично відносно сторін AB і AC, отримаємо точки A2 і A3 відповідно (рис. 86). Довжина трьохланкової ламаної A3B1C1A2 дорівнює периметру трикутника A1В1С1. Для того, щоб периметр був найменшим (дорівнював відрізку A2А3), необхідно, щоб вершини B1 і C1 лежали у точках перетину відрізка A2А3 зі сторонами трикутника AB і AC. Залишилося зрозуміти, як вибрати точку A1 на стороні BC так, щоб довжина відрізка A2А3 була найменшою. Зазначимо, що трикутник A2АА3 – рівнобедрений (A3А = А2А = А1А), а кут при його вершині A:
Доведення теореми Фаньяно. Нехай точки A1, B1, C1 лежать на сторонах трикутника ABC (A1 – на стороні BC і т. д.). Відобразимо точку A1 симетрично відносно сторін AB і AC, отримаємо точки A2 і A3 відповідно (рис. 86). Довжина трьохланкової ламаної A3B1C1A2 дорівнює периметру трикутника A1В1С1. Для того, щоб периметр був найменшим (дорівнював відрізку A2А3), необхідно, щоб вершини B1 і C1 лежали у точках перетину відрізка A2А3 зі сторонами трикутника AB і AC. Залишилося зрозуміти, як вибрати точку A1 на стороні BC так, щоб довжина відрізка A2А3 була найменшою. Зазначимо, що трикутник A2АА3 – рівнобедрений (A3А = А2А = А1А), а кут при його вершині A: ![]() і тому не залежить від вибору точки A1 (рис. 87).
і тому не залежить від вибору точки A1 (рис. 87).
Отже, рухаючи точку A1 по стороні BC, кут A2АА3 не змінюється. А його лінійні розміри будуть найменшими, коли найменшою буде сторона A2А, що дорівнює A1А. Отже, A1А – висота, проведена до сторони BC.
Помічаємо, що існує єдиний вписаний трикутник найменшого периметра, його вершина A1 – основа висоти. Якщо провести такі ж міркування з вершинами B1 і C1, отримаємо, що вони теж є основами висот (оскільки трикутник мінімального периметру – єдиний!)
ІV. Застосування
Задача 3.3.1. У трикутнику ABC кут В дорівнює 70˚. Знайдіть інші кути трикутника, якщо відомо, що кут між відрізками АН і АО (де т. Н – ортоцентр, т. О – центр описаного кола) дорівнює 400 [12, 16].
Задача 3.3.2. Висота і медіана трикутника, проведені всередині нього з однієї вершини, різні й утворюють однакові кути зі сторонами, що виходять з тієї самої вершини. Визначте радіус описаного кола та величину кута, з якого вони виходять, якщо відомо, що медіана дорівнює m [12, 18].
Задача 3.3.3. Відновити трикутник АВС за точками А, О, Н [12, 17].
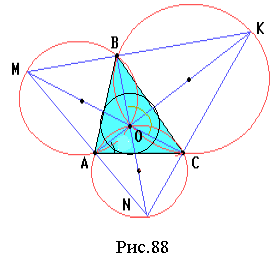 Задача 3.3.4. Доведіть, що радіуси описаних кіл трикутників АВС, ВНС, АНС та АНВ рівні (рис.80) [12, 20].
Задача 3.3.4. Доведіть, що радіуси описаних кіл трикутників АВС, ВНС, АНС та АНВ рівні (рис.80) [12, 20].
Задача 3.3.5. Точка O належить трикутнику ABC і має властивість: прямі АО, BO і CO проходять через центри описаних кіл трикутників BCO, ACO і ABO (рис.88). Доведіть, що O – центр вписаного кола трикутника ABC.
![]() V. Домашнє завдання
V. Домашнє завдання
Задача 3.3.6. Основи висот гострокутного трикутника АВС утворюють трикутник ![]() (рис.81). Доведіть, що
(рис.81). Доведіть, що ![]() АН1Н2 =
АН1Н2 = ![]() Н3Н1В,
Н3Н1В, ![]() Н1Н3В =
Н1Н3В = ![]() Н2Н3С,
Н2Н3С, ![]() Н3Н2С =
Н3Н2С = ![]() АН2Н1.
АН2Н1.
Задача 3.3.7. Доведіть, що трикутники АН3Н2, Н1ВН2, Н1Н3С, АВС подібні (рис. 83) [17, 28].
Задача 3.3.8. Намалюйте інший варіант рисунка 83, на якому кут при вершині А – тупий. Яке з вищевказаних висновків (фактів) мають бути змінені [там само]?
Задача 3.3.9. Доведіть, що ортоцентр тупокутного трикутника є центром зовнівписаного кола до ортотрикутника [там само].
Розділ IV. “Світ Ейлера”
Мета дидактична: ознайомити учнів з прямою та колом Ейлера; навчити їх застосовувати здобуті знання;
розвивальна: розвивати пізнавальну активність учнів; формувати в учнів уміння вбачати красу тверджень, формул, гіпотез, доведень тощо;
виховна: виховувати культуру усної та письмової математичної мови, науковий світогляд, самостійність та ініціативність.
Обладнання: інформаційно-комунікаційні засоби для показу запланованих рисунків та тесту.
Методика введення теми
- Перевірка домашнього завдання
- Тест “Цікаві відомості” (на 10хв.).
1. Який великий російський письменник склав задачник з арифметики
л) О. С. Пушкін
с) Л. М. Толстой
к) М. В. Гоголь
о) О. С. Грибоєдов
р) Ф. М. Достоєвський
2. Розповідають, що Птолемей одного разу запитав Евкліда, чи немає в геометрії коротшого шляху, ніж його 13 книг «Початки», на що той відповів... Отже, що відповів Евклід?
в) У геометрії немає царських доріг.
а) Геометрія – це загадка.
д) Хто шукає, той завжди знаходить.
м) Немає нічого неможливого.
є) Працюйте, і всі вершини будуть ваші.
3.У якому європейському місті є вулиці Піфагора, Архімеда, Ньютона, Коперника?
ф) Барселона,
ц) Берлін,
ю) Мюнхен,
о) Прага,
і) Амстердам.
- Сойєр стверджував, що «У завданнях, які ставить перед нами життя, екзаменатором є..?». (Продовжіть.)
п) Бог.
д) Ти сам.
р) Саме життя.
т) Сама природа.
с) Всесвіт.
5. На якій будівлі було написано «Той, хто не знає геометрію, не може увійти сюди».
є) на будівлі школи Піфагора
е) на будівлі академії Платона
у) на будівлі школи Демокріта
о) на будівлі Мілетської школи
а) на будівлі Елєйської школи
6. Яке число є основним у ряді Священних чисел?
ь) число 1,
и) число 2,
й) число 3,
к) число 4,
я) число 5,
Коментар: число 3 означає:
1) Минуле, сьогодення і майбутнє; 2) Народження, життя і смерть; 3) У сім'ї: отець, мати і дитина; 4) Людина, як і Бог, єдина в трьох особах (тіло, душа і дух).
7. У відомій казці цар послав Андрія за «тридев'ять земель»: «Піди туди не знаю куди, принеси те – не знаю що». Тридев'ять – це скільки?
л) 3∙9,
к) 39,
п) 93,
х) ![]() ,
,
н) ![]() .
.
8. Як з числом 3 пов'язаний тризубець?
є) Тризубець - символ потрійного життя.
а) Тризубець - символ сили, духу і мужності; символ Власті.
ф) Тризубець - символ повітря, землі і води.
в) Тризубець - символ морського володарства.
е) Тризубець - символ потрійного вогню: стихія неба, повітря і води; символ Вічності.
9. Кому належать слова: “Математичний талант – це перш за все наполеглива добре організована праця”.
р) С. Ковалевській,
о) Евкліду,
к) Платону,
ж) Канту,
у) Піфагору.
10. Що в перекладі означає слово хорда.
о) дорога,
с) коротший шлях,
ч) під радугою,
я) співучий народ,
а) тятива лука.
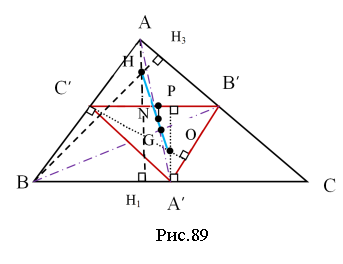 Учитель: Якщо Ви вірно дали відповіді на запитання, то поєднавши обрані Вами літери у слова, Ви прочитаєте назву теми сьогоднішнього заняття – “Світ Ейлера”. (Учитель коментує вірні відповіді.)
Учитель: Якщо Ви вірно дали відповіді на запитання, то поєднавши обрані Вами літери у слова, Ви прочитаєте назву теми сьогоднішнього заняття – “Світ Ейлера”. (Учитель коментує вірні відповіді.)
Далі пригадаємо, що таке серединний трикутник і розглянемо рисунок 89. На ньому трикутник А̕В̕С̕ є серединним трикутником. Дві медіани АА̕ і ВВ̕ перетинаються у точці G (чим ця точка є для трикутника АВС?), дві висоти трикутника АВС – в точці Н і дві висоти трикутника А̕В̕С̕ – в точці О (чому?) (т.О – центр описанного навколо трикутника АВС кола). Дивно, як багато цікавого можна знайти, лише досліджуючи рисунок.
По-перше, сторони трикутника А̕В̕С̕ паралельні сторонам трикутника АВС (чому?), тому ці трикутники подібні. Далі, С̕В̕ = ![]() ВС (чому?), тому відношення довжин будь-яких відповідних відрізків (а не лише відповідних сторін) буде дорівнювати 1:2. Доречі, точка Р – середина відрізка С̕В̕ – водночас середина відрізка АА̕ (оскільки АС̕А̕В̕ паралелограм). Тому медіани трикутника А̕В̕С̕ лежать на медіанах трикутника АВС, а це означає, що обидва трикутника мають один і той же центроїд G.
ВС (чому?), тому відношення довжин будь-яких відповідних відрізків (а не лише відповідних сторін) буде дорівнювати 1:2. Доречі, точка Р – середина відрізка С̕В̕ – водночас середина відрізка АА̕ (оскільки АС̕А̕В̕ паралелограм). Тому медіани трикутника А̕В̕С̕ лежать на медіанах трикутника АВС, а це означає, що обидва трикутника мають один і той же центроїд G.
Висоти трикутника А̕В̕С̕ є серединними перпендикулярами трикутника АВС. А тому точка О – ортоцентр трикутника А̕В̕С̕ – і є в той же час центром кола, описаного навколо трикутника АВС.
Оскільки точка Н – ортоцентр трикутника АВС, а точка О – ортоцентр подібного йому трикутника А̕В̕С̕, то АН = 2ОА̕. Згадаймо, що точка перетину медіан ділить їх у відношенні 2:1, рахуючи від вершин. Тому АG= 2GA̕.
І останнє, з того, що АН і ОА̕ перпендикулярні стороні ВС, випливає, що вони паралельні. Тому,
![]() НАG =
НАG =![]() ∆НАG подібен ∆ОА̕G
∆НАG подібен ∆ОА̕G
і ![]() .
.
Ми показали, що точки O,G,H колінеарні (лежать на одній прямій) і HG = 2GO, тобто має місце наступна теорема.
ІІI. Засвоєння
![]() Теорема 4.1. Ортоцентр, центроїд і центр описаного кола довільного трикутника лежать на одній прямій. Центроїд поділяє відстань від ортоцентра до центра описаного кола у відношенні 2:1 [17, 28].
Теорема 4.1. Ортоцентр, центроїд і центр описаного кола довільного трикутника лежать на одній прямій. Центроїд поділяє відстань від ортоцентра до центра описаного кола у відношенні 2:1 [17, 28].
|
Пряма, на якій лежать ортоцентр, центроїд і центр описаного кола довільного трикутника, називається прямою Ейлера цього трикутника |
Ім’я Ейлера з’являється так часто і в таких різноманітних областях математики, що слід сказати про нього декілька слів.
“Ейлер обчислював без жодних видимих зусиль, як людина дихає або як орел летить над землею” – писав Д. Араго.
“Ейлер у математиці – це Моцарт у музиці, Пушкін в поезії, Мікеланджело в живопису” – наголошував М. І. Кованцов.
|
|
Повертаємося до рисунку 89. Ми відмітили точку N, де пряма Ейлера НО перетинає пряму, що проходить через точку Р перпендикулярно відрізку В̕С̕. Усі три прямі AH, PN і A̕O паралельні (чому?). Оскільки АР = РА̕, то пряма PN рівновіддалена від прямих АН і A̕O. Тому, точка N – середина відрізка НО.
Якщо провести ті ж самі міркування для будь-якої іншої сторони трикутника А̕В̕С̕, то відрізок НО залишатиметься тим же, і він ділитиметься навпіл серединним перпендикуляром до нової сторони. А тому усі серединні перпендикуляри трикутника А̕В̕С̕ перетинаються у точці N, тобто N – центр описаного навколо трикутника А̕В̕С̕ кола. Його радіус дорівнює половині радіуса описаного навколо трикутника АВС кола (бо ці трикутники подібні і точка N – середина відрізка НО).
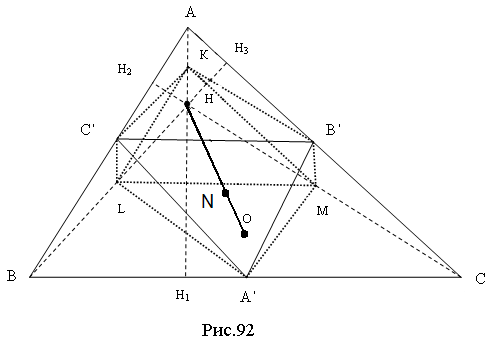 Розглянемо рисунок 91, на якому K, L, M – середини відрізків АН, ВН, СН. Оскільки ВС – спільна сторона трикутників АВС і НВС, а точки С̕, В̕ і L, M – середини інших їх сторін відповідно, то відрізки С̕В̕ і LM паралельні прямій ВС ( а їх довжини дорівнюють половині відрізка ВС).
Розглянемо рисунок 91, на якому K, L, M – середини відрізків АН, ВН, СН. Оскільки ВС – спільна сторона трикутників АВС і НВС, а точки С̕, В̕ і L, M – середини інших їх сторін відповідно, то відрізки С̕В̕ і LM паралельні прямій ВС ( а їх довжини дорівнюють половині відрізка ВС).
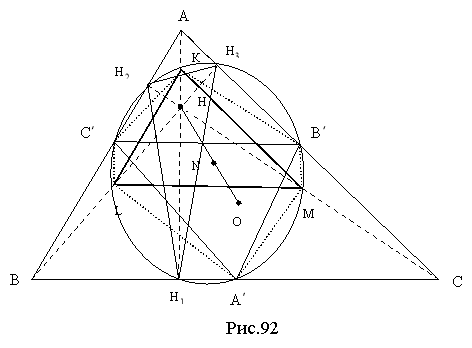 Звідси, С̕L і B̕M – паралельні прямій АН (а їх довжини дорівнюють половині відрізка АН). Тому, B̕C̕LM – прямокутник, аналогічно А̕В̕KL і C̕A̕MK. Тому A̕K, B̕L, C̕M – діаметри кола (рис. 92).
Звідси, С̕L і B̕M – паралельні прямій АН (а їх довжини дорівнюють половині відрізка АН). Тому, B̕C̕LM – прямокутник, аналогічно А̕В̕KL і C̕A̕MK. Тому A̕K, B̕L, C̕M – діаметри кола (рис. 92).
Оскільки ![]() A̕Н1K – прямий, це коло (побудоване на відрізку А̕K, як на діаметрі) проходить через точку
A̕Н1K – прямий, це коло (побудоване на відрізку А̕K, як на діаметрі) проходить через точку ![]() . Аналогічно, воно пройде через точки
. Аналогічно, воно пройде через точки ![]() і
і ![]() . Узагальнюючи вищесказане, сформулюємо теорему.
. Узагальнюючи вищесказане, сформулюємо теорему.
![]() Теорема 4.2. Основи трьох висот довільного трикутника, середини трьох сторін і середини трьох відрізків, що з’єднують його вершини з ортоцентром, належать одному колу радіуса
Теорема 4.2. Основи трьох висот довільного трикутника, середини трьох сторін і середини трьох відрізків, що з’єднують його вершини з ортоцентром, належать одному колу радіуса ![]() , де R – центр описаного кола [17, 30].
, де R – центр описаного кола [17, 30].
Словами Ейлера: серединний трикутник і ортотрикутник мають спільне описане коло, центром якого буде точка N (див. раніше).
Згідно Ж. В. Понселе, воно називається колом дев’яти точок цього трикутника.
Європейці часто називають це коло «колом Ейлера».
|
ПОНСЕЛЕ Жан Віктор (1788 – 1867рр.) (рис.93) – французький математик і інженер, чл. Парижської АН (1834р.).
|
Пізніше частинний результат Ейлера перевідкрив К. Фейєрбах і тим самим описав нову властивість, яка настільки «чудова», що дехто називає коло дев’яти точок «колом Фейєрбаха».
|
|
![]()
Теорема Фейєрбаха. Коло дев’яти точок дотикається вписаного та усіх зовнівписаних кіл трикутника (у випадку, якщо трикутник рівносторонній, воно співпадає з вписаним колом) (рис. 95) (без доведення) [2, 31].
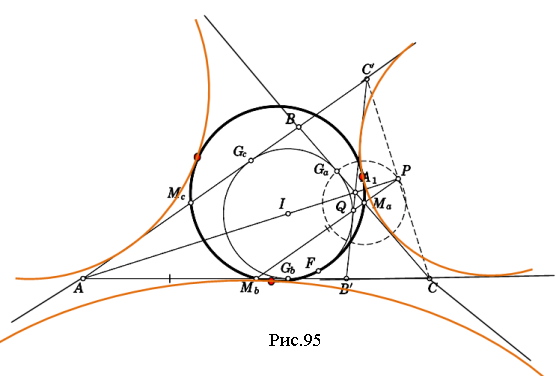 Точку дотику вписаного кола і кола Ейлера називають точкою Фейєрбаха (точка F). Точками Фейєрбаха також іноді називають точки дотику зовнівписаних кіл з колом Ейлера (точки Fa, Fb і Fc) (див. рис. 95).
Точку дотику вписаного кола і кола Ейлера називають точкою Фейєрбаха (точка F). Точками Фейєрбаха також іноді називають точки дотику зовнівписаних кіл з колом Ейлера (точки Fa, Fb і Fc) (див. рис. 95).
ІV. Застосування
Задача 4.1. Доведіть, що ∆АВС є ортотрикутником для ∆ОаОbОc.
Задача 4.2. Доведіть, що R ![]() 2r, де R – радіус описаного кола, r – радіус вписаного кола.
2r, де R – радіус описаного кола, r – радіус вписаного кола.
Задача 4.3. Доведіть, що якщо у трикутнику АВС пряма Ейлера паралельна стороні ВС, то tg![]() B∙ tg
B∙ tg![]() C = 3.
C = 3.
![]() V. Домашнє завдання
V. Домашнє завдання
Задача 4.4. Доведіть, що має місце рівність: ОН2 = 9R2 – a2 – b2 – c2 [17, 31].
Задача 4.5. Доведіть, що чотирикутник АКA̕O (див. рис.91) є паралелограмом [17, 33].
Задача 4.6. Доведіть, що коло описане навколо трикутника АВС, є колом дев’яти точок трикутника ОаОbОc.
 Завдання 4.7. Розгадайте ребус. Запропонуйте свою версію зашифрування прихованого словосполучення.
Завдання 4.7. Розгадайте ребус. Запропонуйте свою версію зашифрування прихованого словосполучення.
Розділ V. Педальний трикутник
Мета дидактична: формувати уміння і навички розв’язування нестандартних задач; ознайомити учнів з педальним трикутником; навчити їх свідомо застосовувати отримані теоретичні відомості до розв’язування задач;
розвивальна: розвивати логічне мислення, пізнавальну активність учнів, самостійність, творчість, ініціативу; пробуджувати інтерес до історії математики;
виховна: виховувати графічну культуру; формувати цікавість до математики.
Обладнання: інформаційно-комунікаційні засоби для показу запланованих рисунків.
Методика введення теми
- Перевірка домашнього завдання
- Вступ
Перш ніж розпочинати нову тему, вчитель пропонує учням “завдання для розігріву”.
№1. Скільки трикутників зображено на рисунку 96?
Відповідь: 24 трикутника.
 №2. Якщо побудувати рівносторонній трикутник зі стороною у п’ять більярдних куль (рис.97), то в такий трикутник можна помістити три кулі. Скільки куль можна буде помістити у трикутник зі стороною у вісім куль? Із скількох куль складатиметься отриманий трикутник?
№2. Якщо побудувати рівносторонній трикутник зі стороною у п’ять більярдних куль (рис.97), то в такий трикутник можна помістити три кулі. Скільки куль можна буде помістити у трикутник зі стороною у вісім куль? Із скількох куль складатиметься отриманий трикутник?
Відповідь: у трикутник зі стороною у вісім куль поміститься 15 куль; отриманий трикутник складатиметься з 36 куль.
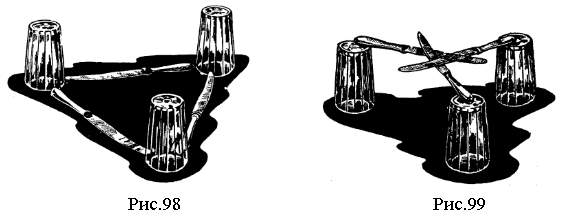 №3. Три стакани розміщені так, що відстань між ними більша довжини кожної з лінійок, які лежать між ними (рис.98). Зробіть з цих трьох лінійок мости, що з’єднували б усі три стакани.
№3. Три стакани розміщені так, що відстань між ними більша довжини кожної з лінійок, які лежать між ними (рис.98). Зробіть з цих трьох лінійок мости, що з’єднували б усі три стакани.
Відповідь: необхідно розмістити лінійки так, як показано на рисунку 99. Кожна лінійка упирається одним кінцем в стакан, а протилежним – в іншу лінійку, що в свою чергу, упирається також у лінійку. Лінійки взаємно підтримують одна одну.
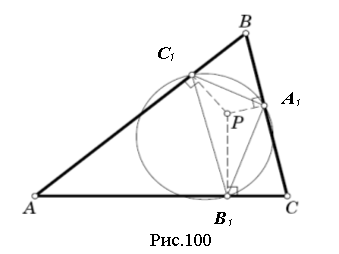 Учитель: ми продовжуємо вивчати захоплюючу фігуру – трикутник, і сьогодні на занятті ми узагальнимо поняття ортотрикутника і серединного трикутника. Для цього розглянемо будь-яку точку Р всередині даного трикутника АВС, і проведемо перпендикуляри РА1, РВ1 і РС1 з точки Р на сторони ВС, СА і АВ відповідно (рис. 100).
Учитель: ми продовжуємо вивчати захоплюючу фігуру – трикутник, і сьогодні на занятті ми узагальнимо поняття ортотрикутника і серединного трикутника. Для цього розглянемо будь-яку точку Р всередині даного трикутника АВС, і проведемо перпендикуляри РА1, РВ1 і РС1 з точки Р на сторони ВС, СА і АВ відповідно (рис. 100).
|
|
На запитання, звідки така назва: “подерний (педальний) трикутник”, відповісти можна лише таким чином: подера (у перекладі з грецької мови – нога) кривої l відносно точки Р – це множина основ перпендикулярів, проведених з точки Р на дотичні до кривої l [28, 465]. Отже, основи перпендикулярів асоціюються зі словом нога (подера), а, оскільки, педальний трикутник утворений з трьох основ перпендикулярів, то і назва його відповідна.
Точку Р можна також обрати ззовні трикутника АВС, при умові, що вона не належатиме описаному навколо трикутника АВС колу (цей випадок розглянемо пізніше).
Якщо точка Р – ортоцентр (Р = Н), то отримаємо ортотрикутник, а якщо вона – центр описаного кола (Р = О), то отримаємо серединний трикутник.
Повертаючись до рисунка 100, видно, що прямі кути в точках С1 і В1 вказують на те, що ці точки належать колу з діаметром АР; іншими словами, точка Р належить колу, описаному навколо трикутника АВ1С1 (Чому?). Застосуємо до цього трикутника і трикутника АВС теорему синусів:
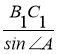 = АР,
= АР, ![]() = 2R.
= 2R.
Звідси В1С1 = 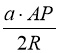 . Аналогічно С1А1 =
. Аналогічно С1А1 = ![]() і А1В1=
і А1В1= ![]() .
.
ІІI. Засвоєння
Таким чином, нами доведена теорема.
![]() Теорема 5.1. Якщо відстані від педальної точки до вершини трикутника АВС є рівними x, y, z, то довжини сторін педального трикутника дорівнюють:
Теорема 5.1. Якщо відстані від педальної точки до вершини трикутника АВС є рівними x, y, z, то довжини сторін педального трикутника дорівнюють: ![]() ,
, ![]() ,
, ![]() , де R – радіус описаного кола навколо трикутника АВС[17, 35].
, де R – радіус описаного кола навколо трикутника АВС[17, 35].
![]() Зауваження
Зауваження
У окремому випадку, коли точка Р є центром описаного кола (x =y = z = r), довжини сторін педального трикутника дорівнюють:
![]() ,
, ![]() ,
, ![]() .
.
![]()
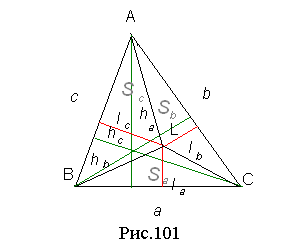 Теорема 5.2. Якщо з точки L у трикутнику АВС проведені перпендикуляри la, lb, lс, відповідно на сторони а, b, с трикутника, то
Теорема 5.2. Якщо з точки L у трикутнику АВС проведені перпендикуляри la, lb, lс, відповідно на сторони а, b, с трикутника, то
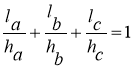 .
.
Доведення. З'єднаємо точку L з вершинами трикутника. Трикутник АВС розіб'ється на три трикутники (рис.101). Позначимо площі цих трикутників Sа, Sb, Sc. Тоді:
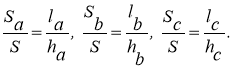
Склавши ліві і праві частини рівностей, отримаємо
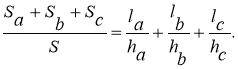
Оскільки Sa + Sb + Sc = S, то 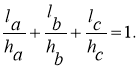
![]() Наслідок. У рівносторонньому трикутнику сума відстаней від довільної точки, узятої в трикутнику, до його сторін, є величина постійна, що дорівнює висоті трикутника. (Перевірити самостійно.)
Наслідок. У рівносторонньому трикутнику сума відстаней від довільної точки, узятої в трикутнику, до його сторін, є величина постійна, що дорівнює висоті трикутника. (Перевірити самостійно.)
Далі, перейдемо до дуже цікавої задачі, в якій розглядаються педальні трикутники педальних трикутників. Вона в той же час чудово демонструє роль уяви в геометрії.
|
|
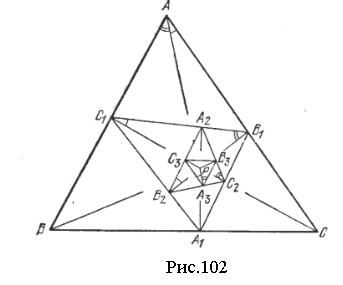
На рисунку 102 внутрішня точка Р використана для визначення трикутника ![]()
![]()
![]() (першого) педального трикутника трикутника АВС. Та ж сама педальна точка Р використовується для визначення «другого педального трикутника»
(першого) педального трикутника трикутника АВС. Та ж сама педальна точка Р використовується для визначення «другого педального трикутника» ![]()
![]()
![]() трикутника
трикутника ![]()
![]()
![]() і «третього педального трикутника»
і «третього педального трикутника» ![]()
![]()
![]() трикутника
трикутника ![]()
![]()
![]() . В цих термінах відкриття Нейберга можна виразити наступним чином:
. В цих термінах відкриття Нейберга можна виразити наступним чином:
![]() Теорема 5.3. Тертій педальний трикутник подібний первинному.
Теорема 5.3. Тертій педальний трикутник подібний первинному.
Доведення. Необхідно з’єднати точки Р і А. Якщо розглянути кола, описані навколо трикутників АВ1![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() , то точка Р належить кожному з них, тому
, то точка Р належить кожному з них, тому
![]()
![]() АР =
АР = ![]()
![]()
![]() Р =
Р = ![]()
![]()
![]() Р =
Р = ![]()
![]()
![]() Р =
Р = ![]()
![]()
![]() Р =
Р = ![]()
![]()
![]() Р
Р
і
![]() РА
РА![]() =
= ![]() Р
Р![]()
![]() =
= ![]() Р
Р![]()
![]() =
= ![]() Р
Р![]()
![]() =
= ![]() Р
Р![]()
![]() =
= ![]() Р
Р![]()
![]() .
.
Іншими словами, дві частини, на які пряма АР ділить кут А, мають двійників: одна – при вершині ![]() , а інша – при вершині
, а інша – при вершині ![]() , далі – при вершинах
, далі – при вершинах ![]() і
і ![]() , і, нарешті, обидві – при вершині
, і, нарешті, обидві – при вершині ![]() . Звідси, трикутник АВС і трикутник
. Звідси, трикутник АВС і трикутник ![]()
![]()
![]() мають рівні кути при вершинах А і
мають рівні кути при вершинах А і ![]() . Аналогічно, вони мають рівні кути при вершинах В і
. Аналогічно, вони мають рівні кути при вершинах В і ![]() . Отже, трикутник АВС подібний до трикутника А3В3С3.
. Отже, трикутник АВС подібний до трикутника А3В3С3.
Цікаво простежити на рисунку «хід кутів» з положення А у положення ![]() – такий же чіткий, як і маневри вимуштруваної команди.
– такий же чіткий, як і маневри вимуштруваної команди.
|
Він з’ясував, що n-й педальний n-кутник будь-якого n-кутника подібен первинному n-кутнику. |
ІV. Застосування
Задача 5.1. Задано рівносторонній трикутник АВС і довільна точка Р. Доведіть, що з відрізків АР, ВР, і СР можна скласти трикутник (теорема Помпейю).
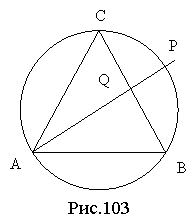 Задача 5.2. Доведіть, що якщо продовження чевіани AQ (рис.103) рівностороннього трикутника АВС перетинає описане коло в точці Р, то
Задача 5.2. Доведіть, що якщо продовження чевіани AQ (рис.103) рівностороннього трикутника АВС перетинає описане коло в точці Р, то
![]() +
+ ![]() =
= ![]() [17, 37].
[17, 37].
Задача 5.3. Нехай АВС – рівнобедрений трикутник з кутами 80˚ при вершинах В і С. Чевіана BD поділяє кут В на кути в 60˚ і 20˚, а чевіана СЕ поділяє кут С на кути в 30˚ і 50˚, як на рисунку104. Знайдіть ![]() EDB [17, 38].
EDB [17, 38].
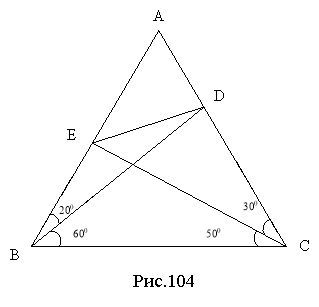
![]() V. Домашнє завдання
V. Домашнє завдання
Завдання на дослідження. Проведіть побудову для четвертого педального чотирикутника деякого чотирикутника, подібну як для третього педального трикутника для трикутника АВС (рис. 102). Простежте «хід кутів».
Задача 5.4. Визначте сторони педального трикутника точки OI (центра вписаного кола) відносно трикутника АВС.
Задача 5.4. Визначте сторони педального трикутника точки G (центра тяжіння трикутника) відносно трикутника АВС.
Розділ VI. Прямі Сімсона
Мета дидактична: навчити учнів поєднувати математичну і нематематичну інформацію, продовжувати формувати в учнів уміння розв’язувати геометричні задачі, свідомо застосовуючи теоретичні відомості;
розвивальна: удосконалювати уміння виділяти головне, розвивати уміння узагальнювати, аналізувати, співставляти;
виховна: виховувати науковий світогляд; удосконалювати уміння користуватися інформаційно-комунікційними засобами.
Обладнання: інформаційно-комунікаційні засоби для показу запланованих рисунків, слайда.
Методика введення теми
- Перевірка домашнього завдання
- Вступ
 Учитель: ми з Вами розглядали багато прикладів використання трикутників у житті людей. Насправді, це лише незначна їх частина. Сьогодні ми розглянемо комбінацію двох трикутників та їх практичне значення. Перш за все, наведіть приклади фігур, що утворені комбінацією трикутників взагалі і комбінацією двох трикутників зокрема (випуклі та невипуклі багатокутники).
Учитель: ми з Вами розглядали багато прикладів використання трикутників у житті людей. Насправді, це лише незначна їх частина. Сьогодні ми розглянемо комбінацію двох трикутників та їх практичне значення. Перш за все, наведіть приклади фігур, що утворені комбінацією трикутників взагалі і комбінацією двох трикутників зокрема (випуклі та невипуклі багатокутники).
Розглянемо рисунок 105. Заданий чотирикутник, утворений з двох рівнобедрених трикутників. Яку назву має задана фігура? Що вона Вам нагадує, і де її можна зустріти?
![]() Учитель: ця фігура має назву дельтоїд. Його форма нагадує повітряного змія.
Учитель: ця фігура має назву дельтоїд. Його форма нагадує повітряного змія.
Змій повітряний – прив'язний літальний апарат, що важчий за повітря. Підтримується у повітрі тиском вітру на поверхню, спрямовану під деяким кутом до напряму руху вітру і яку утримує леєр із землі.
![]() Перші згадки про повітряних зміїв зустрічаються ще у II столітті до н.е., у Китаї (так званий змій-дракон).
Перші згадки про повітряних зміїв зустрічаються ще у II столітті до н.е., у Китаї (так званий змій-дракон).

 Довгий час змії не знаходили практичного застосування. З другої половини XVIII ст. їх починають широко використовувати при проведенні наукових досліджень атмосфери. У 1749 р. шотландський астроном А. Вільсон (1714—1786рр.) за допомогою повітряного змія проводив вимірювання температури повітря на висоті. У 1752 р. американський вчений Б. Франклін (1706–1790рр.) провів експеримент, в якому за допомогою змія виявив електричну природу блискавки і надалі, завдяки отриманим результатам, винайшов громовідвід. Російський вчений світового значення М. В. Ломоносов (1711–1765рр.) проводив аналогічні експерименти і незалежно від Франкліна отримав такі ж результати.
Довгий час змії не знаходили практичного застосування. З другої половини XVIII ст. їх починають широко використовувати при проведенні наукових досліджень атмосфери. У 1749 р. шотландський астроном А. Вільсон (1714—1786рр.) за допомогою повітряного змія проводив вимірювання температури повітря на висоті. У 1752 р. американський вчений Б. Франклін (1706–1790рр.) провів експеримент, в якому за допомогою змія виявив електричну природу блискавки і надалі, завдяки отриманим результатам, винайшов громовідвід. Російський вчений світового значення М. В. Ломоносов (1711–1765рр.) проводив аналогічні експерименти і незалежно від Франкліна отримав такі ж результати.
 Досліди атмосферної електрики були надзвичайно небезпечними. 26 червня 1753 року при запуску змія у грозу загинув колега М. В. Ломоносова, російський академік Г. В. Ріхман (1711–1753рр.).
Досліди атмосферної електрики були надзвичайно небезпечними. 26 червня 1753 року при запуску змія у грозу загинув колега М. В. Ломоносова, російський академік Г. В. Ріхман (1711–1753рр.).
У XIX столітті змії також широко застосовувалися для метеорологічних спостережень.
На початку XX сторіччя повітряні змії використано при створенні радіо. Російський фізик і електротехнік О. С. Попов (1859–1906рр.) використовував змій для підйому антен на значну висоту.
Важливо відзначити використання повітряних зміїв при розробці перших літаків. Зокрема, контр-адмірал, піонер авіації О. Ф. Можайський (1825–1890рр.), перш ніж почати будівництво свого літака, провів серію випробувань з повітряними зміями, які тягнула упряжка коней. На підставі результатів цих випробувань були вибрані розміри літака, що забезпечили йому достатню підйомну силу.
Практичні можливості повітряного змія привертали увагу військових. У 1848 р. російський вчений і винахідник в області артилерії, ракетної техніки К. І. Константинов (1818–1871рр.) розробив систему порятунку суден, що потерпають невдач поблизу берега, за допомогою повітряних зміїв. Під час першої світової війни війська різних країн застосовували змій для підйому на висоту спостерігачів-корегувальників артилерійського вогню, розвідки ворожих позицій.
Трикутники не припиняють дивувати. Доречи, ми ще зустрінемося сьогодні з назвою дельтоїда.
- Засвоєння
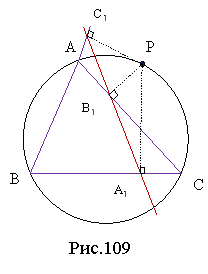 Повернемося до педального трикутника і розглянемо випадок, коли точка Р (педальна точка) належить описаному колу (рис. 109). Для визначеності будемо вважати, що точка Р належить дузі СА, що не містить точку В.
Повернемося до педального трикутника і розглянемо випадок, коли точка Р (педальна точка) належить описаному колу (рис. 109). Для визначеності будемо вважати, що точка Р належить дузі СА, що не містить точку В.
Усі інші випадки можуть бути отримані перепозначенням вершин літерами А, В, С. Оскільки кути РА1С, РВ1С, РС1 А– прямі, то точка Р також належить колам, описаним навколо трикутників А1ВС1, А1В1С і АВ1С1.
Тому ![]() АРС = 1800 –
АРС = 1800 – ![]() В =
В = ![]() С1РА1
С1РА1
І, віднімаючи ![]() АРА1, маємо, що
АРА1, маємо, що
![]() А1РС =
А1РС = ![]() С1РА.
С1РА.
Але оскільки точки А1,С,Р,В1 належать описаному навколо трикутника А1В1С колу, то
![]() А1РС =
А1РС = ![]() А1В1С
А1В1С
Оскільки точки А, В1, Р, С1 належать описаному навколо трикутника А1ВС1 колу, маємо ![]() С1РА =
С1РА = ![]() С1 В1А. Таким чином,
С1 В1А. Таким чином, ![]() А1 В1С =
А1 В1С = ![]() С1В1А. Звідси, точки А1 ,В1, С1 – колінеарні, тобто педальний трикутник «вироджується». Навпаки, якщо точка Р розміщена таким чином, що педальний трикутник трикутника АВС вироджується, то точка Р повинна лежати в одному з кутів трикутника АВС і поза протилежною йому стороною. Перепозначивши вершини, якщо це необхідно, ми можемо припустити, що цей «один кут» є кутом В і що точка С1 належить продовженню сторони ВА за точку А(рис. 109). Повторюючи вищевикладене про кути, але в оберненому порядку, ми можемо отримати, що точка Р належить описаному навколо трикутника АВС колу. Цим ми довели теорему.
С1В1А. Звідси, точки А1 ,В1, С1 – колінеарні, тобто педальний трикутник «вироджується». Навпаки, якщо точка Р розміщена таким чином, що педальний трикутник трикутника АВС вироджується, то точка Р повинна лежати в одному з кутів трикутника АВС і поза протилежною йому стороною. Перепозначивши вершини, якщо це необхідно, ми можемо припустити, що цей «один кут» є кутом В і що точка С1 належить продовженню сторони ВА за точку А(рис. 109). Повторюючи вищевикладене про кути, але в оберненому порядку, ми можемо отримати, що точка Р належить описаному навколо трикутника АВС колу. Цим ми довели теорему.
![]() Теорема 6.1. Основи перпендикулярів, проведених з точки на сторони трикутника колінеарні (лежать на одній прямій) тоді і тільки тоді, коли ця точка належить описаному навколо даного трикутника колу [17, 54].
Теорема 6.1. Основи перпендикулярів, проведених з точки на сторони трикутника колінеарні (лежать на одній прямій) тоді і тільки тоді, коли ця точка належить описаному навколо даного трикутника колу [17, 54].
|
|
|
|
Пряма Сімсона має багато цікавих властивостей. Розглянемо рис.110, який повторює рис.109, за винятком перпендикуляра РА1, продовженого до перетину з описаним колом у точці U, і додатково добудованою прямою АU.
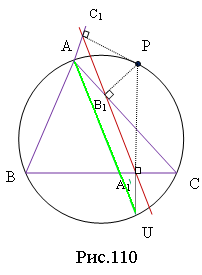 Оскільки РАUC і РВ1А1С – вписані чотирикутники, то
Оскільки РАUC і РВ1А1С – вписані чотирикутники, то
![]() РUА =
РUА = ![]() РАС =
РАС =![]() РСВ1 =
РСВ1 = ![]() РА1В1.
РА1В1.
Тому відрізок АU паралельний прямій Сімсона (проходить через точки А1, В1).
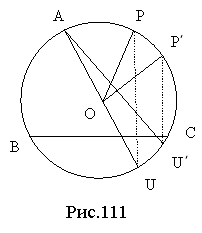 Порівняємо пряму Сімсона точки Р з прямою Сімсона іншої точки Р΄ (належить тому ж описаному колу). Кут між цими двома прямими Сімсона дорівнює куту UАU΄ між паралельними їм прямими АU і АU΄ (рис.111). Дві хорди РU і Р΄U΄ перпендикулярні відрізку ВС, паралельні одна одній і відтинають рівні дуги РР΄ і UU΄. Таким чином,
Порівняємо пряму Сімсона точки Р з прямою Сімсона іншої точки Р΄ (належить тому ж описаному колу). Кут між цими двома прямими Сімсона дорівнює куту UАU΄ між паралельними їм прямими АU і АU΄ (рис.111). Дві хорди РU і Р΄U΄ перпендикулярні відрізку ВС, паралельні одна одній і відтинають рівні дуги РР΄ і UU΄. Таким чином,
![]() UАU΄ =
UАU΄ = ![]() UОU΄ =
UОU΄ = ![]() РОР΄.
РОР΄.
Або, якщо ми розрізняємо додатні та від’ємні кути, то
![]() UАU΄ =
UАU΄ = ![]() UОU΄ =
UОU΄ = ![]() РОР΄.
РОР΄.
Таким чином, нами доведена теорема.

![]() Теорема 6.2. Величина кута між прямими Сімсона двох точок Р і Р΄, що належать описаному колу, дорівнює кутовій мірі величини дуги РР΄ [там само].
Теорема 6.2. Величина кута між прямими Сімсона двох точок Р і Р΄, що належать описаному колу, дорівнює кутовій мірі величини дуги РР΄ [там само].
Якщо ми уявимо, що точка Р рівномірно рухається по описаному колу (учитель показує заготовлений слайд – Додаток С на діску), то пряма АU буде рівномірно обертатися навколо точки А з вдвічі меншою кутовою швидкістю, що і направлена у протилежну сторону; при цьому вона змінює початковий напрямок на протилежний до 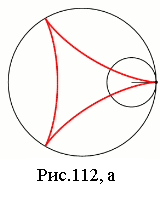 того моменту, коли точка опише повне коло. Тим часом, пряма Сімсона буде рухатися навколо неперервно змінювального центру обертання. Насправді, пряма Сімсона рухаючись, постійно дотикається симетричної
того моменту, коли точка опише повне коло. Тим часом, пряма Сімсона буде рухатися навколо неперервно змінювального центру обертання. Насправді, пряма Сімсона рухаючись, постійно дотикається симетричної 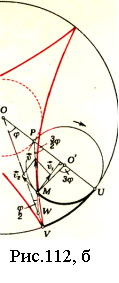 кривої, яка називається дельтоїдою або «гіпоциклоїдою Штейнера» (рис.112, а). А коло з центром у точці О і радіусом ОР – є колом Ейлера (рис.112, б) [7].
кривої, яка називається дельтоїдою або «гіпоциклоїдою Штейнера» (рис.112, а). А коло з центром у точці О і радіусом ОР – є колом Ейлера (рис.112, б) [7].
Дельтоїда (гіпоциклоїда Штейнера) – плоска крива, що описується фіксованою точкою кола, що котиться по внутрішній стороні іншого кола, радіус якого втричі більший за радіус першого.
![]() Назву крива отримала за схожість з грецькою літерою ∆. Її властивості вперше вивчалися Л. Ейлером у XVIII столітті, а потім Я. Штейнером у XIX ст.
Назву крива отримала за схожість з грецькою літерою ∆. Її властивості вперше вивчалися Л. Ейлером у XVIII столітті, а потім Я. Штейнером у XIX ст.
|
|
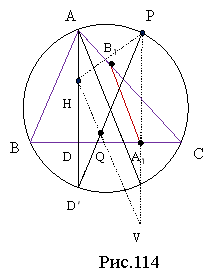 Далі розглянемо рис.114. Оскільки відрізки НD΄ (Н – ортоцентр трикутника АВС) і PV перпендикулярні стороні ВС, то маємо що трикутники QHD΄ і QPV є рівнобедреними. Іншими словами, відрізок HV є образом відрізка D΄P при симетрії відносно прямої ВС. Оскільки
Далі розглянемо рис.114. Оскільки відрізки НD΄ (Н – ортоцентр трикутника АВС) і PV перпендикулярні стороні ВС, то маємо що трикутники QHD΄ і QPV є рівнобедреними. Іншими словами, відрізок HV є образом відрізка D΄P при симетрії відносно прямої ВС. Оскільки
![]() D΄HV =
D΄HV = ![]() PVH =
PVH = ![]() D΄PU =
D΄PU = ![]() D΄AU,
D΄AU,
то пряма HV паралельна прямій AU, яка паралельна прямій Сімсона у точці Р.
І, нарешті, відзначимо, що у трикутнику PHV пряма Сімсона А1В1 паралельна стороні HV і ділить навпіл відрізок PV (у точці А1). Тому, вона також повинна поділяти навпіл сторону PH. Маємо теорему.
![]() Теорема 6.3. Пряма Сімсона точки (що лежить на описаному колі) поділяє навпіл відрізок, що з’єднує цю точку з ортоцентром [там само].
Теорема 6.3. Пряма Сімсона точки (що лежить на описаному колі) поділяє навпіл відрізок, що з’єднує цю точку з ортоцентром [там само].
- Застосування
Задача 6.1. Якщо чотирикутник вписаний у коло, то сума добутків довжин двох пар його протилежних сторін дорівнює добутку довжин його діагоналей (теорема Птолемея). Доведіть [17, 56].
|
|
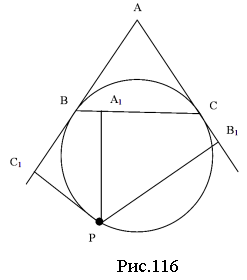 Задача 6.2. Дано дві дотичні до кола, що дотикаються його у точках В і С та перетинаються в точці А. Нехай А1, В1, С1 – педальний трикутник рівнобедреного трикутника АВС для довільної точки Р на цьому колі (див. рис.116). Доведіть, що тоді виконується рівність:
Задача 6.2. Дано дві дотичні до кола, що дотикаються його у точках В і С та перетинаються в точці А. Нехай А1, В1, С1 – педальний трикутник рівнобедреного трикутника АВС для довільної точки Р на цьому колі (див. рис.116). Доведіть, що тоді виконується рівність: ![]() [там само].
[там само].
Задача 6.3. Доведіть, що прямі Сімсона діаметрально протилежних точок описаного кола перпендикулярні між собою і перетинаються на колі дев’яти точок [17, 59].
Задача 6.4. Нехай через точку М, що є серединою хорди РQ деякого кола, проведені дві довільні хорди АВ і СD. Хорди AD і ВС перетинають відрізок PQ у точках X і Y. Доведіть, що точка М є серединою відрізка XY (теорема про метелика) [там само].
- Домашнє завдання
Задача 6.5. Нехай трикутник АВС – рівносторонній трикутник, вписаний у коло з центром О, і нехай Р – довільна точка на цьому колі. Доведіть, що тоді пряма Сімсона точки Р поділяє навпіл радіус ОР [там само].
Задача 6.6. Чи потребує наше доведення теореми 6.1 яких-небудь змін для випадку, коли трикутник АВС – тупокутний?
Задача 6.7. Яка точка кола має пряму СА своєю прямою Сімсона?
Задача 6.8. Чи існують які-небудь точки, що лежать на своїй прямій Сімсона? Якими прямими вони можуть бути у цьому випадку?
 Завдання 6.9. Підготуйте доповідь про легендарну людину, прізвище якої зашифроване (під літерами приховані цифри, а під цифрами літери):
Завдання 6.9. Підготуйте доповідь про легендарну людину, прізвище якої зашифроване (під літерами приховані цифри, а під цифрами літери):
, , при умові, що А = 2.
Розділ VII. Трикутники Наполеона
Мета дидактична: ознайомити учнів з трикутниками Наполеона та їх застосуванням;
розвивальна: розвивати пізнавальну активність учнів, пам’ять, увагу, творчість; формувати інтерес до знань; установлювати міжпредметні зв’язки;
виховна: виховувати прагнення до різнобічного розвитку особистості за рахунок видатної історичної постаті, самостійність, ініціативність, наполегливість у роботі.
Обладнання: інформаційно-комунікаційні засоби для показу запланованих рисунків.
Методика введення теми
- Перевірка домашнього завдання
Учні виступають з докладами про людину-легенду – Наполеона Бонапарта (біографічні відомості, його захоплення, свої враження тощо).
Наприклад:
|
|
Відомо, що Наполеон Бонапарт займався математикою, й особливо він цікавився геометрією. Розповідають, що одного разу Наполеон, тоді ще не правитель Франції, дискутував з великими математиками Лагранжем і Лапласом. Під час якої Лаплас його різко перервав: “Менш за все ми хочемо від вас, генерал, уроку з геометрії”. Надалі Лаплас став його головним воєнним інженером.
Доповнення учителя: теорему, яку ми сьогодні розглянемо, приписують Наполеону, хоча є сумнівними його знання з геометрії, аналогічно як і знання англійської мови для формулювання відомого паліндрома:
ABLE WAS I ERE I SAW ELBE.
Сенс цього паліндрома можна перевести так: “я був сильним, доки не побачив Ельбу (річка у Німеччині)”.
Завдання: проявити творчість, і придумати якомога більше слів, словосполучень, фраз – паліндромів. Виконання цього завдання буде оцінено на наступному занятті.
- Засвоєння
Розглянемо просту теорему, яка дивним чином була упущена математиками з виду.
![]() Теорема 7.1. Нехай на сторонах довільного трикутника побудовані на зовнішню сторону деякі трикутники, із властивість, що сума їх “віддалених” кутів дорівнює 1800. Тоді кола, описані навколо цих трикутників, мають спільну точку [17, 81].
Теорема 7.1. Нехай на сторонах довільного трикутника побудовані на зовнішню сторону деякі трикутники, із властивість, що сума їх “віддалених” кутів дорівнює 1800. Тоді кола, описані навколо цих трикутників, мають спільну точку [17, 81].
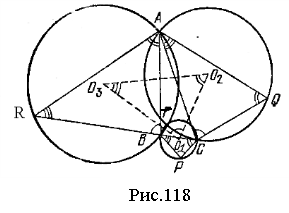 Доведення. Нехай маємо, як на рисунку 118, трикутники СВР, АСQ, ВАR, побудовані на сторонах заданого трикутника АВС і підібрані так, що кути Р, Q, R задовольняють умові
Доведення. Нехай маємо, як на рисунку 118, трикутники СВР, АСQ, ВАR, побудовані на сторонах заданого трикутника АВС і підібрані так, що кути Р, Q, R задовольняють умові ![]() P +
P + ![]() Q +
Q + ![]() R = 1800. Кола, описані навколо трикутників СВР і АСQ, перетинаються у точці С, а другу точку їх перетину позначимо через Т. З’єднаємо точку Т з точками А, В, С. Маємо
R = 1800. Кола, описані навколо трикутників СВР і АСQ, перетинаються у точці С, а другу точку їх перетину позначимо через Т. З’єднаємо точку Т з точками А, В, С. Маємо
![]() ВТС = 1800 –
ВТС = 1800 – ![]() Р,
Р, ![]() СТА = 1800 –
СТА = 1800 – ![]() Q,
Q,
тому
![]() АТВ = 3600 – (
АТВ = 3600 – (![]() ВТС +
ВТС + ![]() СТА) = 3600 – (1800 –
СТА) = 3600 – (1800 – ![]() Р + 1800 –
Р + 1800 – ![]() Q) =
Q) =
= ![]() Р +
Р + ![]() Q =1800 –
Q =1800 – ![]() R.
R.
Отже, точка Т належить не лише колу, описаному навколо трикутників СВР і АСQ, але і колу, описаному навколо трикутника ВАR.
Далі, розглянемо випадок, коли на сторонах довільного трикутника побудовані рівносторонні трикутники. Підкреслимо, що теорема 7.1 для такого випадку справедлива (поясніть чому?). Тоді описані навколо рівносторонніх трикутників кола називаються колами Торрічеллі, а точка їх перетину – точкою Торрічеллі [15]. Вона має таку властивість, що сума відстаней від неї до трьох даних точок є мінімальною.
 Питання про знаходження такої точки має давню історію. Ним цікавилися найвидатніші вчені епохи Відродження – італійський математик Кавальєрі (1598–1647рр.), Торрічеллі та ін. Така властивість точки Торрічеллі застосовується при вирішенні різних техніко-економічних завдань. Наприклад, розглянемо таке завдання: у місцях Р1, Р2, Р3 здобуваються деякі матеріали, що споживають на центральній станції Р. Де необхідно побудувати Р, щоб вартість доставки вантажів з Р1, Р2, Р3 до пункту Р була найменшою? Відповідь: Р – точка Торрічеллі для трикутника Р1 Р2 Р3.
Питання про знаходження такої точки має давню історію. Ним цікавилися найвидатніші вчені епохи Відродження – італійський математик Кавальєрі (1598–1647рр.), Торрічеллі та ін. Така властивість точки Торрічеллі застосовується при вирішенні різних техніко-економічних завдань. Наприклад, розглянемо таке завдання: у місцях Р1, Р2, Р3 здобуваються деякі матеріали, що споживають на центральній станції Р. Де необхідно побудувати Р, щоб вартість доставки вантажів з Р1, Р2, Р3 до пункту Р була найменшою? Відповідь: Р – точка Торрічеллі для трикутника Р1 Р2 Р3.
|
У 1644 році розвинув теорію атмосферного тиску, довів можливість отримання так званої «торічеллієвої порожнечі» і винайшов ртутний барометр. У основній праці з механіки «Про рух вільно падаючих і кинутих важких тіл» (1641р.) розвивав ідеї Галілея про рух, сформулював принцип руху центрів тяжіння, заклав основи гідравліки, довів формулу для швидкості закінчення ідеальної рідини з судини.
Окрім виготовлення зорових труб і телескопів, займався конструюванням простих мікроскопів, що складаються всього з однієї крихітної лінзи, яку він отримував з краплі скла (розплавляючи над полум'ям свічки скляну паличку). Саме такі мікроскопи набули потім широкого використання. На його честь названа одиниця тиску торр (міліметр ртутного стовпа). |
П’єр Ферма з’ясував, що при з’єднанні віддалених вершин рівносторонніх трикутників, побудованих на довільному трикутнику, з протилежними їм вершинами заданого трикутника, утворені прямі перетинаються у точці Торрічеллі. Тому, цю точку ще називають точкою Ферма.
|
Праці П. Ферма надихали любителів математики всього світу протягом трьох століть. |
Якщо розглянути вписані чотирикутники РВТС, ВТАR і АТСQ, їх кути (рис.121):
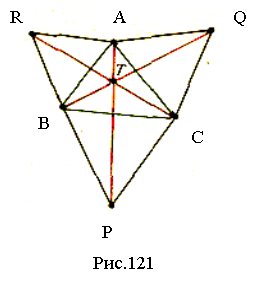
![]() Р =
Р = ![]() R =
R = ![]() Q = 600,
Q = 600,
то має місце рівність:
|
|
Далі, сформулюємо теорему.
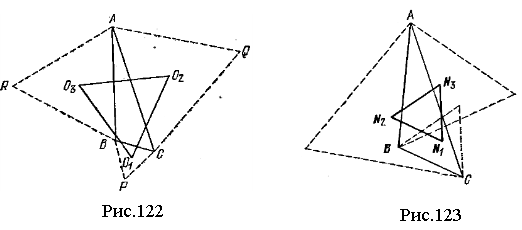
![]() Теорема 7.2. Якщо на сторонах довільного трикутника (∆АВС) на зовнішню сторону побудовані рівносторонні трикутники (СВР, АСQ, ВАR), то їх центри (О1, О2, О3) утворюють рівносторонній трикутник (рис.122) [там само].
Теорема 7.2. Якщо на сторонах довільного трикутника (∆АВС) на зовнішню сторону побудовані рівносторонні трикутники (СВР, АСQ, ВАR), то їх центри (О1, О2, О3) утворюють рівносторонній трикутник (рис.122) [там само].
Саме цю теорему приписують Наполеону.
|
Трикутник з центрів О1О2О3 називають зовнішнім трикутником Наполеона для трикутника АВС (рис.122).
|
Тому, теорему 7.2 можна переформулювати у наступному вигляді:
Зовнішній трикутник Наполеона є рівностороннім.
Доведемо цю теорему методом російського математика і педагога, автора відомих навчальних і освітніх книг з математики І. М. Яглома (1921-1988рр.). Він цікавий тим, що з його допомогою також доводиться аналогічна теорема.
![]() Теорема 7.3. Внутрішній трикутник Наполеона є рівностороннім.
Теорема 7.3. Внутрішній трикутник Наполеона є рівностороннім.
Доведення. Оскільки АО2 – радіус кола, описаного навколо рівностороннього трикутника зі стороною СА = b, то його довжина дорівнює ![]() . Аналогічно, АО3 =
. Аналогічно, АО3 = ![]() .
.
Окрім того, ![]() О3АО2 =
О3АО2 = ![]() А + 600.
А + 600.
За теоремою косинусів для трикутника АО3О2 маємо:
![]()
Оскільки вершини N2 і N3 внутрішнього трикутника Наполеона можна одержати з точок О2 і О3 симетрією відносно прямих СА і АВ відповідно, а ![]() N3AN2 =
N3AN2 = ![]() А – 600, то маємо
А – 600, то маємо
![]()
Віднімаючи між собою останні дві рівності, отримаємо
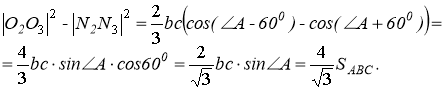
Аналогічно,
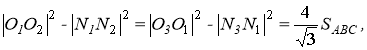
а оскільки ![]() , отримаємо
, отримаємо
![]() .
.
Якщо пригадати, що площа рівностороннього трикутника дорівнює ![]() , помноженому на квадрат довжини його сторони, можемо сформулювати проміжний результат:
, помноженому на квадрат довжини його сторони, можемо сформулювати проміжний результат:
![]() Теорема 7.4. Різниця площ зовнішнього і внутрішнього трикутників Наполеона довільного трикутника АВС дорівнює площі трикутника АВС.
Теорема 7.4. Різниця площ зовнішнього і внутрішнього трикутників Наполеона довільного трикутника АВС дорівнює площі трикутника АВС.
- Застосування
Задача 7.1. Із позначень рисунка 122 доведіть, що:
а) прямі РО1, QО2, RО3 проходять через точку О – центр кола, описаного навколо трикутника АВС;
б) прямі АО1, ВО2, СО3 конкурентні;
в) відрізки АР, ВQ, СR рівні між собою (відрізки, що розглядав Ферма) [17, 82].
Задача 7.2. У позначеннях рисунка 123 прямі АN1, BN2, CN3 конкурентні. Доведіть [там само].
Задача 7.3. Зовнішній і внутрішній трикутники Наполеона мають спільний центр. Доведіть [там само].
- Домашнє завдання
Підготуватися до тестування за темою “Геометрія трикутника”.
Розділ VIII. Підсумкове заняття
Мета дидактична: за допомогою моделювання реальних життєвих ситуацій узагальнити і перевірити знання і уміння учнів з теми “Геометрія трикутника”, навчитися застосовувати отримані знання для розв’язання практичних завдань;
розвивальна: встановити між предметні зв’язки; розширити світогляд студентів; розвинути уявлення про математику як частину загальнолюдської культури, підкреслити значущість математичних знань в історії цивілізації і сучасному суспільстві; розвиток навичок спільної діяльності, комунікативних умінь, відповідальності за колективне рішення;
виховна: виховувати прагнення до різнобічного розвитку особистості за рахунок цікавих завдань, самостійність, ініціативність, наполегливість у роботі.
Обладнання: інформаційно-комунікаційні засоби для показу запланованих рисунків.
Методика проведення підсумкового заняття
- Перевірка домашнього завдання
- Комп’ютерний тест
Учні за комп’ютером відповідають на запитання тесту (Додаток Е).
Час, що залишається відводиться на гру.
 Гра: “Цей чудернацький світ трикутника”
Гра: “Цей чудернацький світ трикутника”
Клас ділиться навпіл. Кожна половина самостійно визначається, хто з учнів потрапить до складу команди (більша кількість учнів), а хто – до складу її помічників.
Гра передбачає наявність двох команд, підтримку кожної команди, незалежне журі (можливо учні старших класів або вчителі різних предметів) і ведучого, яким є вчитель математики.
Гру краще проводити з використанням мультимедійного проектора.
Учні визначаються з назвами своїх команд, які мають бути пов’язані з курсом “Геометрія трикутника”. Напередодні гри кожна команда має скласти завдання для суперників (або запитання по курсу, або задача для розв’язання з курсу, або завдання творчого характеру – продемонструйте…, прокоментуйте…, опишіть…тощо з ілюстраціями та відповіддю для журі), що буде оцінюватись у 10 балів для команди, яка виконала завдання і у 10 балів за оригінальність для команди, що запропонувала це завдання.
Правила гри: команди мають можливість користуватися формулами, що виписані в окрему таблицю (зошит, блокнот тощо). Команди працюють самостійно. Якщо необхідна допомога зі сторони
- помічників, то команда при цьому віддає 2 бали своїм суперникам,
- ведучого, то кожна його підказка оцінюється 2 балами для суперників.
Помічники, окрім того, що можуть допомагати команді при необхідності, будуть отримувати свої завдання.
Якщо команда виконує завдання II туру швидше, то за швидкість команді додається 1 бал.
I тур. РОЗМИНКА
“Задача на швидкість” для двох команд (1 хв. на виконання):
 з шести сірників або рівних паличок складіть чотири рівносторонніх трикутника. (Фігуру необхідно будувати не на площині, а у просторі.) (3 бали)
з шести сірників або рівних паличок складіть чотири рівносторонніх трикутника. (Фігуру необхідно будувати не на площині, а у просторі.) (3 бали)
Відповідь: розв’язком задачі є рис.1. Розкладіть на столі з трьох спічин трикутник, а інші три поставте так, щоб вони своїми нижніми кінцями упирались в кути трикутника, що лежить на столі, а верхніми кінцями з’єдналися над його серединою, – і Ви виконаєте завдання.
Доповнення ведучого: на мал.1 зображене геометричне тіло – правильна трьохгранна піраміда, або її ще називають “тетраедром”, що обмежений чотирма рівними між собою рівносторонніми трикутниками [Игнатьев Е.И. В царстве смекалки: В 3 книгах – книга 1. – 4-е изд. – С.-Петербург, 1914, 275с.].
Для помічників команд (1 хв. на виконання):
На листі формата А4 зробити змістовний малюнок з використанням трикутників. Переможе той, у кого малюнок буде найбільш реальний (2 бала) і буде використано найбільшу кількість трикутників (1 бал).
II тур. У СВІТІ ІСТОРІЇ (на виконання кожного завдання 5 хв.)
- “Задача на увагу”. Учитель читає історичні відомості, серед яких буде одна з умов задачі. Учні мають уважно прослухати інформацію, занотувати собі, на їх погляд найважливіше, і необхідне використати при розв’язанні задачі. (5 балів)
 Передмова. МЕГАЛІТИ. У III-II тисячоліттях до н.е. з'явилися споруди з величезних кам'яних брил - мегаліти (від греч. «мегас» – «великий» і «літос» – «камінь»). До мегалітічних споруд відносяться менгіри – камені, що стоять вертикально, заввишки більше двох метрів (рис.2); дольмени - декілька заритих в землю каменів, перекритих кам'яною плитою (рис.3); кромлехи - складні споруди у вигляді кругових огорож діаметром до ста метрів з величезних кам'яних брил. Мегаліти були широко розповсюджені: вони знайдені в Західній Европі, Північній Африці, на Кавказі та в інших районах земної кулі. Лише у Франції їх знайдено близько чотирьох тисяч. Призначення цих споруд невідоме.
Передмова. МЕГАЛІТИ. У III-II тисячоліттях до н.е. з'явилися споруди з величезних кам'яних брил - мегаліти (від греч. «мегас» – «великий» і «літос» – «камінь»). До мегалітічних споруд відносяться менгіри – камені, що стоять вертикально, заввишки більше двох метрів (рис.2); дольмени - декілька заритих в землю каменів, перекритих кам'яною плитою (рис.3); кромлехи - складні споруди у вигляді кругових огорож діаметром до ста метрів з величезних кам'яних брил. Мегаліти були широко розповсюджені: вони знайдені в Західній Европі, Північній Африці, на Кавказі та в інших районах земної кулі. Лише у Франції їх знайдено близько чотирьох тисяч. Призначення цих споруд невідоме.
Найзнаменитіша з них – кромлех Стоунхендж (II тисячоліття до н. е.), недалеко від міста Солсбері в Англії. (З цією спорудою Ви вже знайомі.) Стоунхендж побудований зі ста двадцяти кам'яних глиб вагою до семи тонн кожна, а в діаметрі складає тридцять метрів.
Цікаво, що гори Преселлі в Південному Уельсі, звідки, як вважалося, доставляли будівельний матеріал для цієї споруди, знаходяться в двохстах восьмидесяти кілометрах від Стоунхенджа. Проте сучасні геологи вважають, що кам'яні брили потрапили в округ Стоунхенджа з льодовиками з різних місць [Энциклопедия для детей. Т. 7. Искусство. Ч. 1 /Глав. Э68 ред. М.Д. Аксёнова. — М.: Аванта+, 1997. — 688 с.: ил.].
Переходимо до задач. Розглянемо Стоунхендж після реконструкції (рис.4).
Командам пропонуються задачі.
I к. Якщо з’єднати між собою деякі три глиби Стоухенджа, то кути що утворяться, матимуть такі градусні міри: 300, 300, 1200. Знайдіть площу утвореного трикутника.
 Відповідь:
Відповідь: 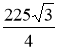 м2 (необхідно використати формулу площі трикутника
м2 (необхідно використати формулу площі трикутника ![]() ).
).
II к. Якщо з’єднати між собою деякі три глиби Стоухенджа, то відстань між ними матиме такі величини: 15м, 20м, 20м. Знайдіть площу утвореного трикутника.
Відповідь: 100 м2 (необхідно використати формулу площі трикутника ![]() ).
).
- “Задача на орієнтування”. Кожній команді надається рисунок 5 (або проектується за допомогою комп’ютерних засобів) і умова задачі. (5 балів)
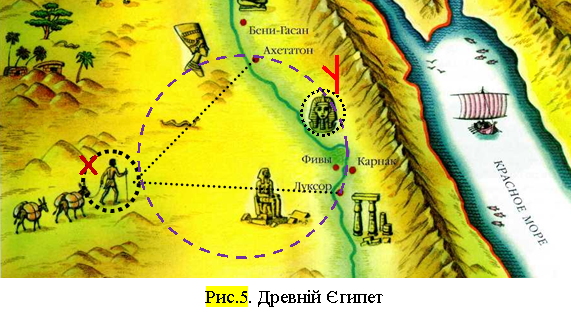 I к. Користуючись рис.5, визначіть відношення відстаней: Y – Ахетатон і Y – Луксор, якщо відомо, що Сфінкс (Y) знаходиться на перетині бісектриси кута Ахетатон – X – Луксор з описаним навколо нього колом.
I к. Користуючись рис.5, визначіть відношення відстаней: Y – Ахетатон і Y – Луксор, якщо відомо, що Сфінкс (Y) знаходиться на перетині бісектриси кута Ахетатон – X – Луксор з описаним навколо нього колом.
Відповідь: відношення відстаней Y – Ахетатон і Y – Луксор дорівнює 1 (якщо рис.5 схематично подати у вигляді рис.6 де Y – це точка W, Ахетатон – точка С, Луксор – точка А, X – точка В, то:
![]() CBW =
CBW = ![]() CAW =
CAW = ![]()
![]() B, як вписані, що спираються на спільну дугу WC;
B, як вписані, що спираються на спільну дугу WC;
![]() ABW =
ABW = ![]() ACW =
ACW = ![]()
![]() B, як вписані, що спираються на спільну дугу AW. Тоді
B, як вписані, що спираються на спільну дугу AW. Тоді ![]() CAW =
CAW = ![]() ACW =
ACW = ![]()
![]() B. Звідси, трикутник АWC – рівнобедрений).
B. Звідси, трикутник АWC – рівнобедрений).
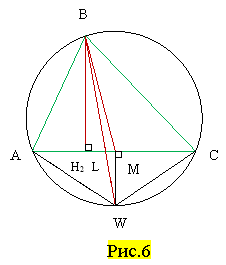 II к. Користуючись рис.5, визначіть відношення кутів: Y – Ахетатон – X і Y – Луксор – X, якщо відомо, що Сфінкс (Y) знаходиться на перетині бісектриси кута Ахетатон – X – Луксор з описаним навколо нього колом.
II к. Користуючись рис.5, визначіть відношення кутів: Y – Ахетатон – X і Y – Луксор – X, якщо відомо, що Сфінкс (Y) знаходиться на перетині бісектриси кута Ахетатон – X – Луксор з описаним навколо нього колом.
Відповідь: відношення кутів Y – Ахетатон– X і Y – Луксор – X дорівнює 1 (пояснення аналогічне).
Помічникам пропонуються умови інших задач (5 балів):
 Помічникам I к. На площадці для дресирування коней виставлені три перепони таким чином, щоб дресирувальник, стоячи на одному місці, міг утримувати коней на відстані 4м (рис. 7). Відомо, що перепона 3 утворює з іншими перепонами кут 300, а відстань від перепони 2 до відрізка, кінцями якого є перепони 1 і 2, дорівнює 4 м. Знайдіть відстані між перепонами.
Помічникам I к. На площадці для дресирування коней виставлені три перепони таким чином, щоб дресирувальник, стоячи на одному місці, міг утримувати коней на відстані 4м (рис. 7). Відомо, що перепона 3 утворює з іншими перепонами кут 300, а відстань від перепони 2 до відрізка, кінцями якого є перепони 1 і 2, дорівнює 4 м. Знайдіть відстані між перепонами.
Відповідь: 8м, 4м, ![]() м (Необхідно використати формули: S∆ =
м (Необхідно використати формули: S∆ = ![]() a∙ha =
a∙ha = ![]() ab∙sinγ,
ab∙sinγ, ![]() , побачити, що трикутник з перепон прямокутний і застосувати теорему Піфагора).
, побачити, що трикутник з перепон прямокутний і застосувати теорему Піфагора).
Помічникам II к. На площадці для дресирування коней виставлені три перепони таким чином, щоб дресирувальник, стоячи на одному місці, міг утримувати коней на відстані 6м (рис. 7). Відомо, що перепона 3 утворює з іншими перепонами кут 300, а відстань від перепони 2 до відрізка, кінцями якого є перепони 1 і 2, дорівнює 3 м. Знайдіть відстані між перепонами.
Відповідь: 6м, 6м, ![]() м (Необхідно використати формули: S∆ =
м (Необхідно використати формули: S∆ = ![]() a∙ha =
a∙ha = ![]() ab∙sinγ,
ab∙sinγ, ![]() побачити, що трикутник з перепон рівнобедрений і застосувати теорему Піфагора).
побачити, що трикутник з перепон рівнобедрений і застосувати теорему Піфагора).
- “Задача про піраміду” (7 балів)
 Передмова: піраміда Хеопса (рис.8) побудована у XXVII ст. до н.е. Її творець - племінник фараона Хеміун. Піраміда (заввишки близько ста сорока семи метрів, зі стороною основи двісті тридцять три метри) складена з блоків золотистого вапняку вагою від двох з половиною до трідцяти тонн. Вони утримуються на місці силою власного тяжіння. Нез'ясовна навіть у наш час та неймовірна точність, з якою кам’яні блоки оброблялися і ставилися один на одного. Зазори між ними не перевищують пів мілліметра. На північній стороні піраміди Хеопса непомітний вхід веде в тісний, а потім більш просторіший коридор (рис.9). Пройшовши по ним, можна потрапити в маленьку ретельно приховану на глибині піраміди похоронну камеру з гранітним, давно спустошеним саркофагом фараона. По вентиляційній системі в камеру потрапляло сухе повітря пустелі, яке сприяло збереженню мумії фараона.
Передмова: піраміда Хеопса (рис.8) побудована у XXVII ст. до н.е. Її творець - племінник фараона Хеміун. Піраміда (заввишки близько ста сорока семи метрів, зі стороною основи двісті тридцять три метри) складена з блоків золотистого вапняку вагою від двох з половиною до трідцяти тонн. Вони утримуються на місці силою власного тяжіння. Нез'ясовна навіть у наш час та неймовірна точність, з якою кам’яні блоки оброблялися і ставилися один на одного. Зазори між ними не перевищують пів мілліметра. На північній стороні піраміди Хеопса непомітний вхід веде в тісний, а потім більш просторіший коридор (рис.9). Пройшовши по ним, можна потрапити в маленьку ретельно приховану на глибині піраміди похоронну камеру з гранітним, давно спустошеним саркофагом фараона. По вентиляційній системі в камеру потрапляло сухе повітря пустелі, яке сприяло збереженню мумії фараона.
Цікаво, що основа піраміди Хеопса в два рази більша ширини Червоної площі у Москві [там само].
I к. Розгляньте переріз піраміди Хеопса (рис.9), яким є рівнобедрений трикутник з висотою – 147 м і основою – 233 м. Якщо погребальну камеру розмістити на перетині бісектрис, то наскільки високо вона опиниться над землею (відповідь округліть до одиниць)?
Відповідь: 56 м. Необхідно використати теорему: кожна бісектриса внутрішнього кута трикутника, точкою перетину, поділяється (рахуючи від вершини кута) у відношенні, що відповідає відношенню суми прилеглих сторін до протилежної.
II к. Розгляньте переріз піраміди Хеопса (рис.9), яким є рівнобедрений трикутник з висотою – 147 м і основою – 233 м. Якщо погребальну камеру розмістити на перетині бісектрис, то наскільки низько вона опиниться від вершини піраміди (відповідь округліть до одиниць)?
Відповідь: 91 м (пояснення аналогічне).
Журі підбиває підсумки за два тури, повідомляє бали команд.
III тур. КРОК У МИСТЕЦТВО
-
 “Задача на швидкість” для двох команд (3 бали)
“Задача на швидкість” для двох команд (3 бали)
Вступ. Ви вже знаєте що таке золоте відношення, а що таке золотий трикутник? Золотим називається такий рівнобедрений трикутник, основа і бічна сторона якого знаходяться в золотому відношенні.
Треба сказати, що в епоху Відродження золотий переріз був дуже популярний серед художників, скульпторів і архітекторів. Чернець Лука Пачолі написав книгу «Божествена пропорція». Леонардо да Вінчі, що знає про вплив золотої пропорції на людину, виконав до цієї книги ілюстрації. Його особа – одна із загадок історії. Сам Леонардо да Вінчі говорив: «Нехай ніхто, не будучи математиком, не наважиться читати мої праці». Немає сумнівів, що Леонардо да Вінчі був великим художником, це визнавали навіть його сучасники, але його особа і діяльність будуть покритими таємницею, оскільки він залишив нащадкам не зв'язний виклад своїх ідей, в якому говориться «про все на світі».
Портрет Монни Лізи (Джоконди) (рис.10) довгий час привертає увагу дослідників, які виявили, що композиція малюнка заснована на золотих трикутниках, що є частинами правильного зірчастого п'ятикутника.
Скульптори, архітектори, художники використовували і використовують золотий переріз у своїх працях, оскільки пропорції золотого перерізу створюють враження гармонії і краси.
Завдання: на портреті Монни Лізи знайдіть чотири однакових золотих трикутника (1 бал) і поясніть їх утворення з геометричної точки зору (2 бали).
Відповідь: чотири однакових золотих трикутника утворюють один великий золотий трикутник. Утворились з великого трикутника проведенням у ньому середніх ліній.

- Завдання: “Я мистецтвознавець” (6 балів) (на 2 хв.)
Командам надається рисунок 11 (або проектується за допомогою комп’ютерних засобів).
Передмова: цей період у творчості В. Кандинського зазвичай називають «холодним» або «класичним». У його роботах пляма все більше поступалася місцем лінії, живопис – сухому геометризму, динаміка – рівновазі…
Завдання: уявіть себе мистецтвознавцем, який презентує композицію на аукціоні відомих людей і продовжіть опис композиції. (Завдання оцінююється за кількістю слів опису (2 бали), цікавістю і нестандртністю презентації (4 бали).)
Помічникам команд пропонується завдання “на швидкість”.
 Необхідно розв’язати “ребусний лабіринт” (рис.12). (3 бали)
Необхідно розв’язати “ребусний лабіринт” (рис.12). (3 бали)
Журі підбиває підсумки за третій тур, повідомляє бали команд.
IV тур. ТВОРЧА ДУЕЛЬ
Кожна команда демонструє свою неординарність, творчим завданням для суперника, яке для кожної команди оцінюється у 10 балів. За цей тур команди мають можливість отримати 20 балів.
У той час помічники команд отримують 2 творчих завдання на вибір (10 балів):
-
 Складіть ребус із зашифрованим словом чи фразою – пов’язаний з курсом “Геометрія трикутника”.
Складіть ребус із зашифрованим словом чи фразою – пов’язаний з курсом “Геометрія трикутника”.
- За одним із заданих малюнків (рис.13) складіть задачу.
- а) напишіть казку геометричного змісту, що була б пов’язана з темою нашого курсу,
- б) будь-яке означення (теорему, властивість, факти) зарифмуйте у жартівливій формі,
- в) зробіть малюнок, тема якого
-“Незвичайне поєднання світу і трикутника”,
-“Хто б міг подумати, що…”,
- своя тема.
Журі підбиває підсумки за всі тури, висловлює враження від роботи учнів і гри загалом, і повідомляє остаточні бали команд. Визначається команда-знавців I cтупеня (переможці гри) і команда II cтупеня (переможені). Командам вручаються дипломи (Додаток E).
ДОДАТКИ
Додаток А
- Загальний опис теми елективного курсу “Геометрія трикутника” для учнів 9 класу

 Курс “Додаткові розділи планіметрії” дає можливість доповнити свою “бібліотеку” знань з такого поняття як “трикутник” і розширити область його практичного застосування. Оскільки “рано чи пізно будь-яка правильна математична ідея знаходить застосування в тій або іншій справі” (О. М. Крилов), то доречним буде на вступному занятті висвітлити значимість трикутників у сфері діяльності людей, тим самим умотивувати вивчення учнями даного курсу. Здійснити сказане можна за допомогою розробленої презентації [54] (рис.1).
Курс “Додаткові розділи планіметрії” дає можливість доповнити свою “бібліотеку” знань з такого поняття як “трикутник” і розширити область його практичного застосування. Оскільки “рано чи пізно будь-яка правильна математична ідея знаходить застосування в тій або іншій справі” (О. М. Крилов), то доречним буде на вступному занятті висвітлити значимість трикутників у сфері діяльності людей, тим самим умотивувати вивчення учнями даного курсу. Здійснити сказане можна за допомогою розробленої презентації [54] (рис.1).
 Ця презентація дозволяє зацікавити учнів до вивчення матеріалу елективного курсу. Для ефективного сприймання нового матеріалу, бажано відтворити у їхній пам’яті необхідні позначення, твердження, формули, факти тощо для подальшої праці. А саме: означення трикутника, його елементи, складові (чудові точки та прямі), види, формули для площі, теореми косинусів, синусів і їх позначення. На цьому етапі можна використати такі математичні програми як: [55] (рис.2), [56] (рис.3), [57] (рис.4), [58] (рис.5), або зкомпановану заздалегідь електронну таблицю.
Ця презентація дозволяє зацікавити учнів до вивчення матеріалу елективного курсу. Для ефективного сприймання нового матеріалу, бажано відтворити у їхній пам’яті необхідні позначення, твердження, формули, факти тощо для подальшої праці. А саме: означення трикутника, його елементи, складові (чудові точки та прямі), види, формули для площі, теореми косинусів, синусів і їх позначення. На цьому етапі можна використати такі математичні програми як: [55] (рис.2), [56] (рис.3), [57] (рис.4), [58] (рис.5), або зкомпановану заздалегідь електронну таблицю.
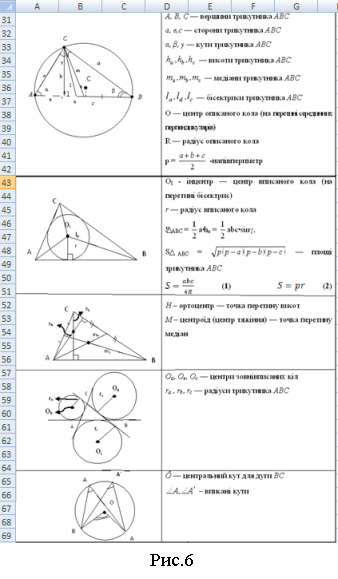
 Оскільки даний курс містить у собі багато нової цікавої для учнів інформації, яка підтримується різноманітними рисунками, то її можна для ефектності та кращого сприйняття і запам’ятовування продемонструвати за допомогою програм [54] та [60] (рис.7).
Оскільки даний курс містить у собі багато нової цікавої для учнів інформації, яка підтримується різноманітними рисунками, то її можна для ефектності та кращого сприйняття і запам’ятовування продемонструвати за допомогою програм [54] та [60] (рис.7).
Кожна з тем даного курсу закріплюється задачами та вправами, які потребують побудови рисунків (елементів трикутників, комбінацій їх з колом та чотирикутником, спеціальних точок тощо). У цьому випадку, на допомогу можуть прийти програми : [56] (рис.8 – інтерактивне геометричне креслення використовується в курсі для показу вирішення завдань крок за кроком, для демонстрації роликів геометричних побудов, для вирішення завдань на побудову), [59] (рис.9), [58] (рис.10 – Редактор чертежей, побудова, як і у попередніх випадках виконється самостійно), [55] (рис.11 – розв’язання підкріплюється заготовленими рисунками) – остання, навіть, зі звуковим супроводом.
Елективний курс містить достатню кількість нової, позашкільної інформації. Деяку її частину можна знайти в [55], [56], [58]. Тому можливі ситуації:
-супроводу нового матеріалу його електронним змістом, рисунками, анімаціями;
-домашнє завдання з використанням ІКТ (задачі з рисунками, можливо, розв’язаннями – для розгляду, повторення вивченого матеріалу);
-самостійний розгляд певної підтеми, з метою продуктивної праці на уроці та кращого засвоєння при розповіді її вчителем.
- Етап актуалізації знань
 Ми пропонуємо актуалізацію знань до уроку з теми “Крокуючи за Піфагором” проводити з використанням інформаційно-комунікаційних технологій. Мета – повторення раніше вивченого матеріалу. Учні заздалегідь готують виступи з використанням презентацій, де можна побачити інформацію про Піфагора, розглянути опорний сигнал (одне із доведень теореми Піфагора (рис.11)) та ін. Якщо необхідно, то вчитель доповнює виступ учнів.
Ми пропонуємо актуалізацію знань до уроку з теми “Крокуючи за Піфагором” проводити з використанням інформаційно-комунікаційних технологій. Мета – повторення раніше вивченого матеріалу. Учні заздалегідь готують виступи з використанням презентацій, де можна побачити інформацію про Піфагора, розглянути опорний сигнал (одне із доведень теореми Піфагора (рис.11)) та ін. Якщо необхідно, то вчитель доповнює виступ учнів.
 Продовжується етап актуалізації розв’язуванням задач. Для цього можна використати програмний продукт [58] (рис.12). Якщо є можливість розсадити учнів по одному за ком’ютер, тоді кожен працює самостійно, в іншому випадку – робота або групова, або колективна, під керівництвом учителя.
Продовжується етап актуалізації розв’язуванням задач. Для цього можна використати програмний продукт [58] (рис.12). Якщо є можливість розсадити учнів по одному за ком’ютер, тоді кожен працює самостійно, в іншому випадку – робота або групова, або колективна, під керівництвом учителя.
Також, останнє можна здійснити за допомогою [57]. Спочатку звернутися до тренажеру (рис.13), а потім до залікових завдань у вигляді тесту (рис.14).
![]()
 Актуалізацію знань до теми “Теорема Нагеля. Чудові відрізки” можна якісно провести за допомогою [56], [58]. В основі нового матеріалу лежить теорема Чеви, яка була розглянута на попередньому занятті. Тому виникає необхідність відтворити ці дані як у: 1) теоретичному вигляді, так і у 2) практичному. Щодо першого пункту, то можна скористатись програмою [56]: а) учні разом формулюють теорему; б) перевіряють відповідь на ПК і при необхідності доповнюють; в) намагаються відтворити доведення цієї теореми; г) порівнюють з доведенням на ПК при натисканні на гіперпосилання Доказательство (рис.16).
Актуалізацію знань до теми “Теорема Нагеля. Чудові відрізки” можна якісно провести за допомогою [56], [58]. В основі нового матеріалу лежить теорема Чеви, яка була розглянута на попередньому занятті. Тому виникає необхідність відтворити ці дані як у: 1) теоретичному вигляді, так і у 2) практичному. Щодо першого пункту, то можна скористатись програмою [56]: а) учні разом формулюють теорему; б) перевіряють відповідь на ПК і при необхідності доповнюють; в) намагаються відтворити доведення цієї теореми; г) порівнюють з доведенням на ПК при натисканні на гіперпосилання Доказательство (рис.16).

Для здійснення другого пункту (застосування теореми Чеви), можна запропонувати учням відтворити домашнє завдання з поясненнями. В завершення перевірити його правильність програмою [58], можна навіть прослухати, як діяти при розв’язуванні даної задачі (рис.17).
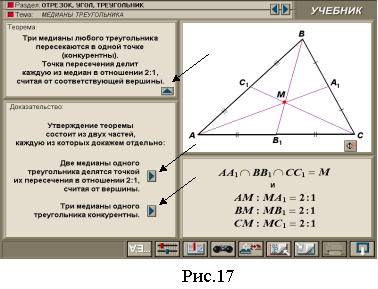
- Етап ознайомлення з новим матеріалом на лекційному занятті
Даний етап розглянемо на прикладі однієї з тем курсу, а саме: “Медіани трикутника”. Для того, щоб провести лекційне заняття з використанням ІКТ, необхідна інтерактивна дошка. Учитель перш ніж розповідати новий матеріал, мотивує учнів, подає цікаву інформацію. Коли настає час нових означень та теорем, учням пропонується програма [58], де є 1 означення, 5 теорем і одна формула з вище згадуваної теми (рис.18). Учитель, спочатку дає можливість учням прослухати деяку інформацію (рис.19), потім звертається до коментарів, пояснень, дискусій.
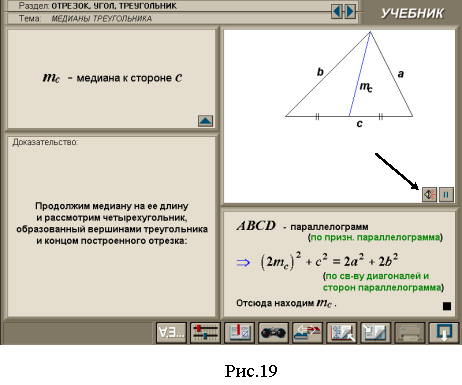
Продемонструвати матеріал з рисунками можна програмою [54]. Наприклад, див. рис.20.
- Етап закріплення вивченого матеріалу на практичному або лабораторному занятті
Оскільки теми, які розглядуються в елективному курсі не входять до шкільних програм, розроблено незначну кількість програмних засобів. Тому етап закріплення вивченого матеріалу пропонуємо провести лише за допомогою програми [58]. ЇЇ можна застосувати при вивченні наступних тем курсу: бісектриси трикутника (рис.21, а), висоти трикутника (рис.21, б) і медіани трикутника (рис.21, в). Для кожної теми пропонуються задачі. Учні самостійно розв’язують завдання, при необхідності отримують консультацію учителя. Після вправ, учням пропонується кросворд з нововивченої теми (рис.22).
5. Етап узагальнення та систематизації знань
Даний етап зазвичай проводиться на завершальному занятті курсу. Виникає необхідність підведення підсумків: узагальнення та систематизації знань. Учитель послідовно повторює основні твердження та теореми курсу. Після чого проводить тест з вивченого курсу за допомогою програми [61] (рис.23).
На завершення учитель проводить дискусію з теми “Мій улюблений урок”. Учні аргументують свої відповіді. Далі, щоб продемонструвати учням використання геометричних фігур у психології, проводиться психогеометричний тест “Типологія особистості”, який можна оформити у вигляді презентації [24].
Додаток В
Відповіді та вказівки до задач.
- Висота тополя 8 футів.
- Глибина ― 12чи, довжина комишу ― 13чи.
-
Висота бамбука ―
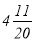 чи.
чи.
- Квітка може відхилитися від вертикалі на 5м.
- Між нижнім кінцем драбини і стіною 44 стопи.
§1.2
- Скористатися формулою (11).
- Скористатися формулою (4).
- Скористатися формулою (10).
-
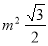 (зробити рисунок за умовою, і виконати додаткову побудову — описати навколо вихідного трикутника коло).
(зробити рисунок за умовою, і виконати додаткову побудову — описати навколо вихідного трикутника коло).
- Розбити заданий трикутник на три трикутники, і для кожного записати формулу площі.
-
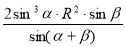 (для знаходження сторін трикутника скористатися теоремою синусів).
(для знаходження сторін трикутника скористатися теоремою синусів).
-
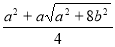 (позначивши катети трикутника через x та y, отримаємо систему:
(позначивши катети трикутника через x та y, отримаємо систему: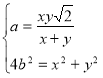 , з якої знайдемо xy).
, з якої знайдемо xy).
§2.1
- Складіть вираз для косинусів двох доповнювальних кутів у точці Х через сторони трикутників ABX і СAX, відповідно.
-
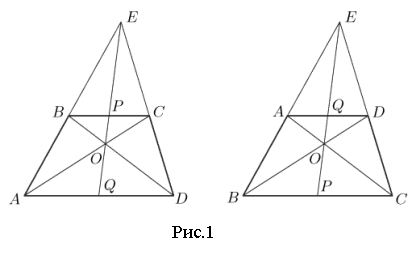 Розглянемо трапецію ABCD з основами AD і ВС, діагоналі якої перетинаються в точці О, а продовження бічних сторін — в точці Е. Проведемо пряму ЕО і позначимо літерами P і Q точки перетину цієї прямої з основами BC і AD (рис.1).
Розглянемо трапецію ABCD з основами AD і ВС, діагоналі якої перетинаються в точці О, а продовження бічних сторін — в точці Е. Проведемо пряму ЕО і позначимо літерами P і Q точки перетину цієї прямої з основами BC і AD (рис.1).
Ми бачимо, що на сторонах трикутника АED (або їх продовженнях) взято точки В, С і Q так, що прямі ВD, АС і EQ перетинаються в одній точці. За теоремою Чеви ![]() .
.
Але згідно теореми Фалеса, ![]() , тому
, тому ![]() . Звідси,
. Звідси, ![]() і тому Q — середина відрізка AD.
і тому Q — середина відрізка AD.
Аналогічно, з точкою P, яка є серединою відрізка ВС.
§3.1
-
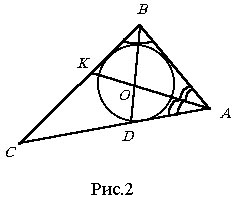 Відповідь:
Відповідь: 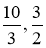
Розв’язання. Нехай BD і AK – бісектриси кутів B і A трикутника ABC (рис.2) і O – центр вписаного кола. Оскільки AB = 4 і BC = 5, то за теоремою 3.1.1. про бісектрису: AD = 4t і CD = 5t, тому AC = 6 = 4t + 5t, тобто ![]() , і тоді
, і тоді ![]() . Тепер знайдемо за теоремою косинусів
. Тепер знайдемо за теоремою косинусів ![]() і
і ![]() . Отже,
. Отже, ![]() .
.
За теоремою 3.1.1. про бісектрису трикутника BAD, знайдемо в якому відношенні точка O поділяє відрізок BD:
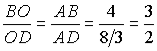
- Відповідь: 10 см.
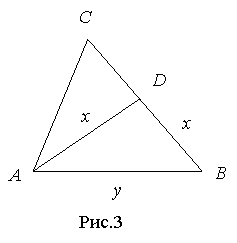 Розв’язання. Проводимо бісектрису AD кута А (рис.3). Трикутник ABD рівнобедрений. Позначимо DA = DB = x см і АВ = y см. За теоремою 3.1.1. про бісектрису матимемо:
Розв’язання. Проводимо бісектрису AD кута А (рис.3). Трикутник ABD рівнобедрений. Позначимо DA = DB = x см і АВ = y см. За теоремою 3.1.1. про бісектрису матимемо: ![]() , звідки
, звідки 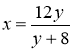 . Запишемо властивість 1 бісектриси у вигляді
. Запишемо властивість 1 бісектриси у вигляді ![]() . З останніх двох рівностей матимемо, що y = 10 см або АВ = 10 см.
. З останніх двох рівностей матимемо, що y = 10 см або АВ = 10 см.
- Відповідь: 1200
Розв’язання. З умови ![]() . Підставивши у властивість № 2 бісектриси, отримаємо
. Підставивши у властивість № 2 бісектриси, отримаємо ![]() .
.
-
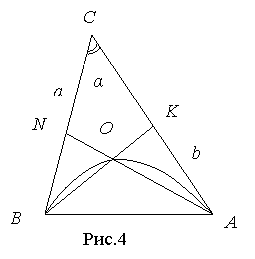 Відповідь:
Відповідь: 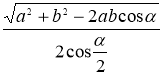
Розв’язання. У трикутнику АВС: ВС = а, АС = b і ![]() (рис.4). Тоді за теоремою косинусів
(рис.4). Тоді за теоремою косинусів ![]() . Точка О ― точка перетину бісектрис BK і AN. Згідно властивості 3 бісектриси,
. Точка О ― точка перетину бісектрис BK і AN. Згідно властивості 3 бісектриси, ![]() . Далі за теоремою синусів для трикутника АОВ отримаємо радіус кола, що проходить через ці точки.
. Далі за теоремою синусів для трикутника АОВ отримаємо радіус кола, що проходить через ці точки.
-
Відповідь:
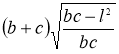
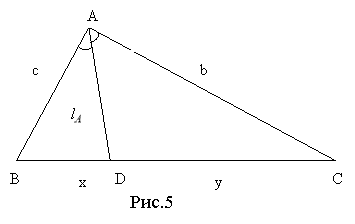 Розв’язання. У трикутнику АВС, згідно умови , АВ = с, АС = b і бісектриса AD =l (рис.5). Позначимо BD = x і СD = y. На основі теореми 3.1.1. про бісектрису та її властивость № 1, запишемо систему
Розв’язання. У трикутнику АВС, згідно умови , АВ = с, АС = b і бісектриса AD =l (рис.5). Позначимо BD = x і СD = y. На основі теореми 3.1.1. про бісектрису та її властивость № 1, запишемо систему 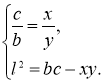 Знайшовши x і y, маємо ВС = x + y.
Знайшовши x і y, маємо ВС = x + y.
- Відповідь: 300
Розв’язання. Позначимо ![]() . Тоді
. Тоді ![]() . Оскільки чотирикутник MNQP вписаний у коло, то
. Оскільки чотирикутник MNQP вписаний у коло, то ![]() , або
, або ![]() . Тому α = 600 і
. Тому α = 600 і ![]() . З умови, що MQ ― бісектриса, випливає, що
. З умови, що MQ ― бісектриса, випливає, що ![]() .
.
§3.2
3.2.1. Доведення. Позначимо довжини сторін трикутника, що відповідають медіанам 5см, ![]() см і
см і ![]() см, через a см, b см і c см. Тоді за властивістю №5 медіан, маємо:
см, через a см, b см і c см. Тоді за властивістю №5 медіан, маємо:
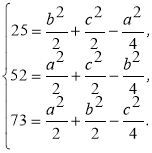
Розв’язуючи цю систему, знаходимо: а2 = 100, b2 = 64 і с2 = 36, тобто b2+ с2 = а2.
За оберненою теоремо Піфагора, робимо висновок, що заданий трикутник – прямокутний.
3.2.2. Відповідь: 4; 6 і 8
Розв’язання. У властивості №5 медіан, позначимо а2 = x, b2 = y і с2 = z. Після піднесення обох частин до квадрату матимемо
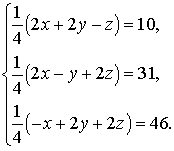
Звідси x = 16, y = 36 и z = 64, а тому сторони треугольника дорівнюють 4; 6 і 8.
3.2.3. Відповідь: ![]() .
.
План розв’язання. 1. У §2.1. при доведенні факту, що серединні перпендикуляри перетинаються в одній точці, йшла мова про те, що вони для серединного трикутника є висотами.
- За формулою (7) таблиці 2 знаходимо площу серединного трикутника.
- За властивістю №1 для серединного трикутника, знаходимо площу вихідного трикутника.
3.2.4. Відповідь: ![]() .
.
Розв’язання. Обчислимо медіану BD за її властивістю №5:
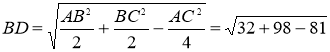 =7.
=7.
Якщо з’єднати точки А та Е, то за оберненою теоремою про властивість бісектриси внутрішнього кута (теорема 3.1.1) трикутника, помічаємо, що АЕ – бісектриса кута А. Тому з трикутника АВD маємо:
![]() ,
, ![]() .
.
За властивістю №1 для бісектриси, знаходимо ![]() .
.
§3.3
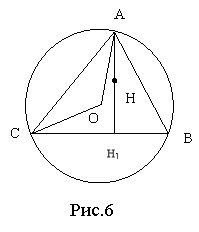 3.3.1. Відповідь:
3.3.1. Відповідь: ![]() А =80°,
А =80°, ![]() С = 30°.
С = 30°.
Розв'язання. Див. рисунок 6. Оскільки відомо, що ![]() CAO =
CAO = ![]() BAH1 = 90° –
BAH1 = 90° – ![]() В, то
В, то
![]() ВАС=2 (90о –
ВАС=2 (90о – ![]() В) + 40° = 80°.
В) + 40° = 80°.
З ∆ABC ![]() ACB = 180˚ –
ACB = 180˚ – ![]() А –
А – ![]() В = 30°.
В = 30°.
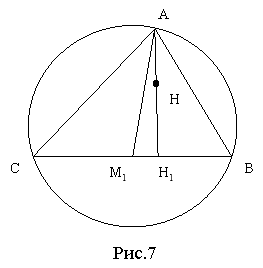 3.3.2. Відповідь: Радіус описаного кола – m; кут, з якого виходять медіана і висота, – 90˚.
3.3.2. Відповідь: Радіус описаного кола – m; кут, з якого виходять медіана і висота, – 90˚.
Розв'язання. Звернемо увагу на рис.7. Оскільки відомо, що відрізки АО і АН утворюють рівні кути з бічними сторонами, то точка О лежить на прямій АМ1. Але відомо також, що точка О належить серединному перпендикуляру до сторони а. Отже, знайдемо точку перетину цих двох прямих. Це точка М1. Отже, М1 ![]() О, радіус описаного кола дорівнює медіані, проведеної до сторони а. Звідси маємо, що радіус описаного кола дорівнює m, і
О, радіус описаного кола дорівнює медіані, проведеної до сторони а. Звідси маємо, що радіус описаного кола дорівнює m, і ![]() А = 90°.
А = 90°.
3.3.3. Розв'язання. Позначимо точку, симетричну ортоцентру відносно сторони а через D (рис.8). З’єднаємо точку А з О. Будуємо коло з центром у точці О і радіусом, що дорівнює АО. З’єднаємо А з Н і продовжимо до перетину з колом у точці D. Серединний перпендикуляр до НD перетне коло в точках В і С, що будуть вершинами шуканого трикутника АВС. З’єднаємо А, В і С. Дістанемо шуканий трикутник АВС.
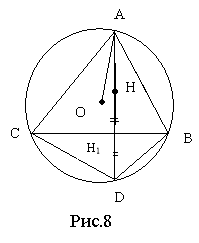 3.3.4. Доведення. Позначимо D точку, симетричну ортоцентру відносно сторони а. R – радіус описаного кола. Спочатку доведемо, що RАВС = RВНС.
3.3.4. Доведення. Позначимо D точку, симетричну ортоцентру відносно сторони а. R – радіус описаного кола. Спочатку доведемо, що RАВС = RВНС.
З міркувань симетрії, ∆ВНС = ∆ВDС. Оскільки чотирикутник АВDС – вписаний, то коло, описане навколо трикутника ВDС, буде одночасно колом трикутника АВС. А оскільки ∆ВНС = ∆ВDС, то RАВС = RВНС.
Аналогічно доводимо, що RАВС = RАНС і RАВС = RАНВ. Звідси маємо, що радіуси описаних кіл трикутників АВС, ВНС, АНС і АНВ рівні.
3.3.5. Доведення. Нехай M, N і K – точки перетину прямих CO, BO і АО з описаними колами трикутників AOB, AOC і ВОС. Оскільки
![]() OAM =
OAM = ![]() OAN =
OAN = ![]() OCN =
OCN = ![]() OCK =
OCK = ![]() OBK =
OBK = ![]() OBM = 90o
OBM = 90o
(як вписані кути, що спираються на діаметри), то МС, NB і KA – висоти трикутника MNK. Тому ABC – ортотрикутник трикутника MNK. Отже, АО, BO і CO – бісектриси кутів трикутника ABC, а точка О – центр вписаного кола трикутника ABC.
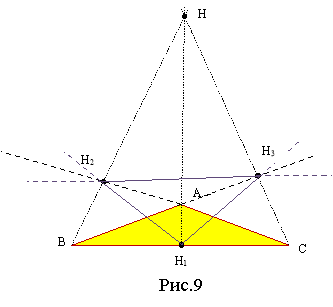 3.3.6. Доведення.
3.3.6. Доведення. ![]() СН1А =
СН1А = ![]() СН1В = 900 (оскільки СН1 – висота, опущена з вершини С на сторону АВ). Також
СН1В = 900 (оскільки СН1 – висота, опущена з вершини С на сторону АВ). Також ![]() Н2Н1С =
Н2Н1С = ![]() СН1Н3, оскільки СН1 – бісектриса кута Н2Н1Н3.
СН1Н3, оскільки СН1 – бісектриса кута Н2Н1Н3.
Тому, ![]() АН1Н2 = 900 –
АН1Н2 = 900 – ![]() Н2Н1С = 900 –
Н2Н1С = 900 – ![]() СН1Н3 =
СН1Н3 = ![]() Н3Н1В. Тоді,
Н3Н1В. Тоді, ![]() АН1Н2 =
АН1Н2 = ![]() Н3Н1В.
Н3Н1В.
Аналогічно, ![]() Н1Н3В =
Н1Н3В = ![]() Н2Н3С,
Н2Н3С, ![]() Н3Н2С =
Н3Н2С = ![]() АН2Н1.
АН2Н1.
3.3.7. Доведення. Оскільки чотирикутник ВСН3Н2 є вписаним (оскільки ![]() ВН3С =
ВН3С = ![]() ВН2С = 900), то
ВН2С = 900), то ![]() АН3Н2 =
АН3Н2 = ![]() В і ∆АН3Н2 подібен ∆АВС. Аналогічно для інших трикутників.
В і ∆АН3Н2 подібен ∆АВС. Аналогічно для інших трикутників.
3.3.8. Розв’язання. Точка Н лежить на внутрішній бісектрисі кута Н3Н1Н2 і на зовнішніх бісектрисах кутів Н1Н3Н2 і Н1Н2Н3 (рис.9).
3.3.9. З попереднього завдання, точка Н – на перетині двох зовнішніх і однієї внутрішньої бісектриси ортотрикутника Н1Н2Н3. А це означає, що точка Н є центром зовнівписаного кола для ортотрикутника.
§4
4.1. Доведення: Покажемо, що ![]() В
В ![]()
![]()
![]() (рис.10).
(рис.10).
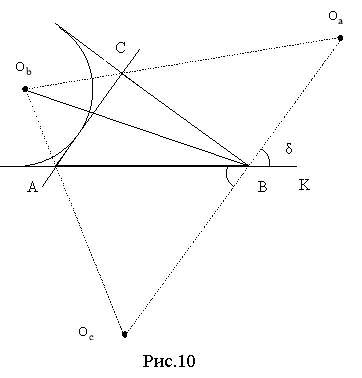 В
В![]() – бісектриса
– бісектриса ![]() СВК.
СВК. ![]() В – бісектриса
В – бісектриса ![]() АВС, тому
АВС, тому ![]()
![]() В
В![]() = 90˚. Аналогічно і з
= 90˚. Аналогічно і з ![]()
![]() А
А![]() і
і ![]()
![]() С
С![]() . Тому ∆АВС – ортотрикутник для ∆
. Тому ∆АВС – ортотрикутник для ∆![]()
![]()
![]() .
.
4.2.Доведення: Побудуємо серединний трикутник A̕B̕C̕ (рис.11). Опишемо навколо нього коло, радіуса ![]() , оскільки це буде коло Ейлера (центр точка N).
, оскільки це буде коло Ейлера (центр точка N).
Якщо це коло не виходить за межі трикутника АВС, то точки A̕, B̕, C̕ співпадають з точками дотику вписаного кола до сторін трикутника (що можливо лише у рівносторонньому трикутнику).
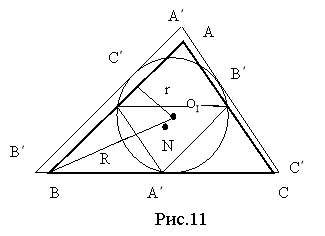 У трикутнику загального вигляду це коло вийде за межі трикутника АВС ( див. рис.11). Проведемо дотичні до кола Ейлера, паралельно відповідним сторонам трикутника. Отримаємо ∆A̕̕B̕̕C̕̕. Усі розміри ∆A̕̕B̕̕C̕̕не менші відповідних розмірів ∆АВС. Тоді радіус r1, вписаного в ∆A̕̕B̕̕C̕̕кола не менший за r , тобто
У трикутнику загального вигляду це коло вийде за межі трикутника АВС ( див. рис.11). Проведемо дотичні до кола Ейлера, паралельно відповідним сторонам трикутника. Отримаємо ∆A̕̕B̕̕C̕̕. Усі розміри ∆A̕̕B̕̕C̕̕не менші відповідних розмірів ∆АВС. Тоді радіус r1, вписаного в ∆A̕̕B̕̕C̕̕кола не менший за r , тобто ![]()
![]() r. А
r. А ![]() =
= ![]() . Тому
. Тому ![]()
![]() r, R
r, R ![]() 2r.
2r.
4.3.Доведення: якщо пряма Ейлера паралельна відрізку ВС, то вона ділить відрізок АD у відношенні 2:1, так що
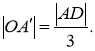
Далі замінимо ![]() наступними виразами:
наступними виразами:
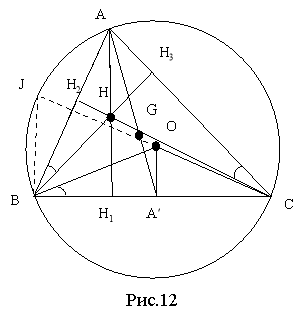
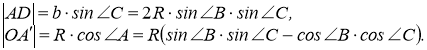
4.4.Доведення: зрозуміло, що (рис.12) 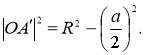 Позначимо
Позначимо ![]() тоді
тоді ![]() і
і ![]() За властивістю медіани, запишемо:
За властивістю медіани, запишемо:
![]()
Застосовуючи теорему Стюарта до трикутника ОАА̕, отримаємо
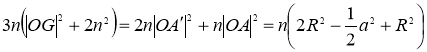
і ![]()
4.5.Доведення: ![]() відрізок ОА̕ паралельний відрізку АК. Тому АКA̕O є паралелограмом.
відрізок ОА̕ паралельний відрізку АК. Тому АКA̕O є паралелограмом.
4.6.Доведення: трикутник АВС є ортотрикутником трикутника ∆ОаОbОc. А описане навколо ортотрикутника коло є колом дев’яти точок.
4.7. Відповідь: педальний трикутник.
§5
-
Доведення. Позначимо СР через z, РВ = y, АР = x. Розглянемо педальний трикутник
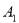
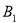
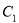 з педальною точкою Р (рис.13).
з педальною точкою Р (рис.13).
За теоремою про відстань від педальної точки до вершин трикутника:
![]()
![]() =
= ![]() ,
, ![]()
![]() =
= ![]() ,
, ![]()
![]() =
= ![]() .
.
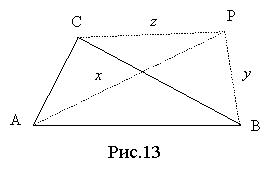 Оскільки, a = b = c = k∙2R (за теоремою синусів)
Оскільки, a = b = c = k∙2R (за теоремою синусів) ![]()
![]() = kz,
= kz, ![]()
![]() = kx,
= kx, ![]()
![]() = ky.
= ky.
Таким чином x ,y, z пропорційні сторонам трикутника А̕В̕С̕ , тобто можна скласти трикутник зі сторонами x, y, z . І він буде подібним до трикутнику А̕В̕С̕.
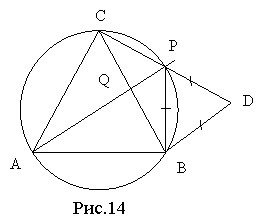 5.2. Доведення. Продовжимо відрізок СР так, щоб виник рівносторонній трикутник BDP (рис.14). Оскільки трикутник DCB подібен до трикутника PCQ, то
5.2. Доведення. Продовжимо відрізок СР так, щоб виник рівносторонній трикутник BDP (рис.14). Оскільки трикутник DCB подібен до трикутника PCQ, то
![]() =
= ![]() = 1 +
= 1 + ![]() .
.
Розділивши останню рівність на DB = PB = DP, отримаємо, що ![]() =
= ![]() +
+ ![]() .
.
5.3. Відповідь: ![]() EDB = 30˚.
EDB = 30˚.
Розв’язання. Проведемо відрізок DF паралельно ВС. Він перетинає відрізок АВ у точці F. Нехай відрізок CF перетинає BD у точці G. Оскільки трикутник BCG рівносторонній, то BG = BC. З того, що трикутник CBE рівнобедрений, випливає що ВЕ = ВС. Звідси, трикутник BGE рівнобедрений, ![]() BGE= 80˚,
BGE= 80˚, ![]() FGE = 40˚. Оскільки
FGE = 40˚. Оскільки ![]() EFG = 40˚, то трикутник FEG рівнобедрений і FE = FG і DF = DG. Тому, трикутник GDE подібне до трикутника FDE, пряма DE поділяє кут FDG навпіл, a
EFG = 40˚, то трикутник FEG рівнобедрений і FE = FG і DF = DG. Тому, трикутник GDE подібне до трикутника FDE, пряма DE поділяє кут FDG навпіл, a ![]() EDB = 30˚.
EDB = 30˚.
5.4. Доведення. Нехай А1В1С1 – педальний трикутник, тоді за теоремою про відстань від педальної точки до вершин трикутника:
![]()
З прямокутного трикутника АВ1Р маємо: АР2 = (p-a)2 + r2,
оскільки АВ1= (р-а), і В1Р = r, де р =![]()
Тоді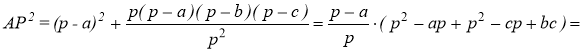
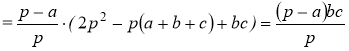 .
.
Тому, 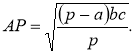
В1С1= а1=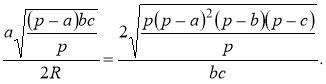
Тому, В1С1= а1=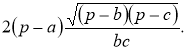
Аналогічно, С1А1= 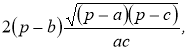 A1B1=
A1B1= 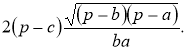
- Доведення. Нехай А1В1С1 – педальний трикутник. Нехай сторони педального трикутника дорівнюють а1, b1, с1.
За теоремою про відстань від педальної точки до вершин трикутника:
![]()
Оскільки, ![]() то
то 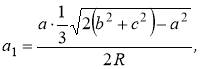
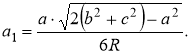
Аналогічно 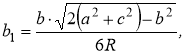
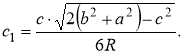
§6
6.1. Доведення. Розглянемо рисунок 109. Не зважаючи на те, що “педальний трикутник” А1В1С1 вироджений, довжини його сторін можна знайти за допомогою теореми про обчислення сторін педального трикутника:
![]()
Оскільки А1В1 + В1С1 = А1С1, маємо, що с∙СР + а∙АР = b∙BP, тобто
АВ∙СР + ВС∙АР = АС∙BP. А АВСР – вписаний чотирикутник.
6.2. Доведення. Проведемо відрізки РВ, РС, С1А1, А1В1. З того, що чотирикутники А1РВ1С і А1ВС1Р вписані, маємо:
![]() А1В1Р =
А1В1Р = ![]() А1СР =
А1СР = ![]() ВСР =
ВСР = ![]() С1ВР =
С1ВР = ![]() С1А1Р,
С1А1Р,
![]() РА1В1 =
РА1В1 = ![]() РСВ1 =
РСВ1 = ![]() РВС =
РВС = ![]() РВА1 =
РВА1 = ![]() РС1А1
РС1А1
і трикутники РА1В1, РС1А1 – подібні.
6.3. Доведення. Нехай ОН – пряма Ейлера трикутника АВС і РР̕ – діаметр описаного навколо нього кола. За теоремою про пряму Сімсона точки, що поділяє навпіл відрізок, який з’єднує цю точку з ортоцентром, прямі Сімсона точок Р і Р̕ поділять навпіл відрізки НР і НР̕, у точках М і М̕ відповідно. Оскільки точки О, М, М̕, N – середини відрізків РР̕, НР, НР̕, ОН, то точка N теж середина відрізка ММ̕. Оскільки NM = ![]() ОР =
ОР = ![]() R є радіусом кола дев’яти точок (теорема 4.2), то відрізок ММ̕ – діаметр. Якщо прямі Сімсона перетинаються у точці X, то
R є радіусом кола дев’яти точок (теорема 4.2), то відрізок ММ̕ – діаметр. Якщо прямі Сімсона перетинаються у точці X, то ![]() MXM̕ = 900 (теорема 6.2), і точка X належить колу дев’яти точок.
MXM̕ = 900 (теорема 6.2), і точка X належить колу дев’яти точок.
6.4. Доведення. Спочатку проведемо перпендикуляри x1 і y1 з точок X і Y на пряму CD (рис.15). Для зручності позначимо а = РМ = MQ, x= XM, y = MY. Якщо розглянути пари подібних трикутників Mx1 (трикутник з вершиною М і протилежною їй стороною х1) і My1, Мх2 і Мy2, Ах1 і Сy2, Dx2 і By1, то можна записати, що
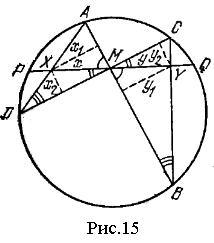
![]()
![]()
![]()
![]()
Звідси,
![]()
і x = y.
6.5. Доведення: у рівносторонньому трикутнику ортоцентр і центр описаного кола співпадають.
6.6. Відповідь: ні.
6.7. Відповідь: точка, діаметрально протилежна точці В.
6.8. Відповідь: вершини трикутника лежать на своїх власних прямих Сімсона.
6.9. Відповідь: Наполеон.
§7
7.1. а) Доведення: РО1, QО2, RО3 – серединні перпендикуляри до сторін трикутника АВС.
б) Доведення: Нехай відрізки АО1, ВО2, СО3 перетинають сторони трикутника АВС у точках X, Y, Z. Тоді
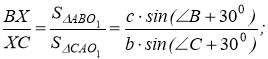
аналогічно для виразів ![]() і
і ![]() , що дає нам можливість застосувати теорему, обернену до теореми Чеви.
, що дає нам можливість застосувати теорему, обернену до теореми Чеви.
в) Доведення: оскільки трикутники РСА і ВСQ рівні за другою ознакою (РС = ВС, АС = СQ – за умовою побудови трикутників Наполеона; ![]() РСА =
РСА = ![]() ВСQ), то РА =ВQ, ВQ = СR.
ВСQ), то РА =ВQ, ВQ = СR.
7.2. Доведення: використати теорему, обернену до теореми Чеви, як у задачі 7.1, б.
7.3. Доведення: уявіть собі, що рисунки 122 і 123 з’єднали. Оскільки шість трикутників BO1N1, CN1O1, CO2N2, AN2O2, AO3N3 i BN3O3 є рівносторонніми, а інші шість трикутників АN3O2, AO3N2, O3BN1, N3BO1, N2O1C, O2N1C подібні трикутнику АВС, то:
N3O2 = O3N2 = BN1 = BO1 = O1С = CN1 = ![]() ,
,
O3N1 = O1N3 = СN2 = СO2 = O2А = N2А = ![]() ,
,
O1N2 = O2N1 = АN3 = АO3 = O3В = N3В = ![]() .
.
З того, що
![]() О1ВО3 =
О1ВО3 = ![]() O1BN1 +
O1BN1 + ![]() N1BO3 = 600 +
N1BO3 = 600 + ![]() B
B
і
![]() ВО3N2 =
ВО3N2 = ![]() BO3A –
BO3A – ![]() N2O3A = 1200 –
N2O3A = 1200 – ![]() B,
B,
слідує, що чотирикутник BO1N2O3 (протилежні сторони якого рівні) є паралелограмом. Якщо через X позначити середину відрізка О2О3, а через В̕ – середину відрізка СА (яка є також серединою відрізка O2N2), то можемо довести, що пряма XB̕ паралельна прямій O3N2 і прямій ВО1. Оскільки ВО1 = 2XB̕, то прямі O1X і ВВ̕ перетинаються у точці G (О1G = 2GX і ВG = 2GВ̕). Але прямі O1X і ВВ̕ є медіанами трикутника О1О2О3 і трикутника АВС. Тому, для цих двох трикутників точка G є їх спільним центроїдом. Змінюючи паралелограм BO1N2O3 на паралелограм BN1O2N3, аналогічно знаходимо, що точка G є також центроїдом трикутника N1N2N3.
Додаток С
Розподіл годин курсу по темах
|
№ n/n |
Назва розділу і теми |
Кількість годин |
Форма контролю |
|
1 |
Вступне заняття |
1 |
- |
|
2 |
Формули для площ трикутників |
4 |
Складання довідкової таблиці |
|
- Крокуючи за Піфагором |
|||
|
- Площа трикутника |
|||
|
3 |
Навколо чудових точок трикутника |
4 |
Співбесіда з учнями |
|
- Чудові точки. Теорема Чеви |
|||
|
- Теорема Нагеля. Чудові відрізки |
|||
|
4 |
Деякі чудові прямі трикутника |
6 |
Написання емпатійного твору |
|
- Бісектриси |
|||
|
- Медіани та серединний трикутник |
|||
|
- Висоти та ортотрикутник |
|||
|
5 |
“Світ Ейлера” |
2 |
Творче завдання на вибір учня |
|
6 |
Педальний трикутник |
2 |
|
|
7 |
Прямі Сімсона |
2 |
|
|
8 |
Трикутники Наполеона |
2 |
|
|
9 |
Підсумкове заняття |
1 |
Тест + гра |
|
Усього |
- |
24 |
- |
Додаток D
|
|
(1) |
|
|
(2) |
|
|
(3) |
|
|
(4) |
|
|
(5) |
|
|
(6) |
|
|
(7) |
|
|
(8) |
|
|
(9) |
|
|
(10) |
|
|
(11) |
|
|
(12) |
|
|
(13) |
|
|
(14) |
|
S= |
(15) |
|
S = |
(16) |

![]()



![]()


СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ
1. Адамар Ж. Элементарная геометрия: Учеб. пособие для высш. пед. учеб. заведений и преподавателей средней школы. – 3-е изд., планиметрия. – М., 1948. – 608с.
- Акопян А.В. Заславский А.А. Геометрические свойства кривих второго порядка. – М.: МЦНМО, 2007. – 136с.
3. Апостолова Г.В. Геометрія: Підручник для 8-го кл. загальноосвіт. навч. закл. – К.: Генеза, 2005. – 256с.
4. Бевз Г.П. Люблю геометрію // Математика в школах України. – 2005. – №10(94) – С.2-8.
5. Белл Э.Т. Творцы математики: Предшественники соврем. Математики. Пособие для учителей. – М.: Просвещение, 1979. – 256с.
6. Белый А.Д. Формула Герона // Квант. – 1986. – №10 – С.20-21.
- Березин В. Дельтоида // Квант. – 1977. – №3 – С.19.
- Буданов В.Г. Синергетичні стратегії в освіті // Вища освіта України. – 2003. – № 2. – С. 7-12.
- Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Шестаков С.А., Юдина И.И. Планиметрия. Пособие для углубленного изучения математики. – М., 2005. – 488с.
- Вакарчук І.О. Сучасна фізико-математична освіта і наука: тенденції та перспективи // Математична газета. – 2008. – №11-12. – С. 1-10.
- Габович И.Г. Алгоритмический поход к решению геометричкеских задач. – К.: Радянська школа, 1989. – 160с.
- Древаль М. Властивості ортоцентра трикутника // Математика в школах України. – 2005. – №34(54) – С.16-20.
- Дубровский В. Шесть доказательств теоремы о медианах // Квант. – 1978. – №4 – С.36-38.
- Ефремов Д. Новая геометрия треугольника. – Одесса: Типография Бланкоиздательства М. Шпенцера, 1902. – 350с.
- Калейдоскоп // Квант. – 1986. – №10 – С.32-33.
- Карпушина Н. М. Развивающие задачи по геометрии. 7 класс. – М.: Школьная Пресса, 2004. – 80 с.
- Коксетер Г.С., Грейтцер С.Л. Новые встречи с геометрией. – М: Наука, 1978. – 224с.
- Концепція профільного навчання в старшій школі / Уклад. Л.Березівська, Н.Бібік, М.Бурда та ін. // Інформаційний збірник Міністерства освіти і науки України. – 2003. – №24. –С.3-15.
- Куланін Є.Д., Федін С.Н. Геометрія трикутника в задачах. – М., 1990. – 144с.
- Курант Р., Роббинс Г. Что такое математика? – 3-е изд., испр. и доп. – М.: МЦНМО, 2001. – 568с.
- Кушнир И.А. Способноконкурирующие отрезки // Математика в школах України. – 2005. – №31(115) – С.9-12.
- Лосєва Н. М., Луковська К. С. Використання комп’ютерних технологій при вивченні спеціальних дисциплін вищої школи // Сучасні тенденції розвитку вищої освіти, трансформація навчального процесу у технологію навчання / Матеріали конференції 23-24 жовтня 2008 року. – К.: Видавництво ДУІКТ, 2008. – С.89.
- Лосєва Н. М., Луковська К. С. Елективні курси з математики як основний інструмент // Проблеми математичної освіти / Матеріали міжнародної науково-методичної конференції 7-9 квітня 2009 року. Черкаси: Вид. від. ЧНУ ім. Б. Хмельницького, 2009. – С. 65-66.
- Лосєва Н. М. Саморозвиток викладача вищої школи: Навчальний посібник. – Донецьк: ДонНУ, 2003. – 336с.
- Луковська К. С. Вивчення геометрії на елективних курсах // Евристика і дидактика математики / Міжнародна науково-методична дистанційна конференція 2009 року.
- Луковська К. С. Прийоми підвищення інтересу учнів до вивчення геометрії на елективних курсах // Якісна освіта ХХІ століття: проблеми і пошуки / Збірник матеріалів Всеукраїнської науково–методичної конференції 14 березня 2009 року: українською та російською мовами (за заг. ред. докт. пед. наук Н. М. Лосєвої). – У 2-х томах. – Том 1. – Донецьк: Вид-во ДонНУ, 2009. – С. 335-338.
- Маралов В. Г. Основы самопознания и саморазвития: Учеб. пособие для студ. сред. пед. учеб, заведений. – 2-е изд., стер. – М.: Издательский центр «Академия», 2004. – 256 с.
- Математика: “Энциклопедия / Под ред. Ю.В.Прохорова. – М.: Большая Российская энциклопедия, 2003. – 845с.
- Мойсеюк Н.Є. Педагогіка. Навчальний посібник. 3-є видання, доповнене, 2001. – 608с.
- Мякишев А.Г. Элементы геометрии треугольника. – М., 2002. – 32с.
- Освітні технології: Навчально-методичний посібник. – К.: А.С.К., 2001. – 256с.
- Педагогічні технології. Досвід. Практика: Довідник. – Полтава: ПОІПОПП, 1999. – 376с.
- Понарин Я.П. Элементарная геометрия: В 2т. – Т. 1: Планиметрия, преобразования плоскости. – М.: МЦНМО, 2004. – 312с.
- Прасолов В.В. Задачи по планиметрии: Учеб. Пособие. – 5-е изд. испр. и доп. – М.: МЦНМО, 2006. – 640с.
- Програма для загальноосвітніх навчальних закладів. Математика. 5-12 класи. – К. – Ірпінь: Перун, 2005. – С.6.
- Протасов В. Ю. Максимумы и минимумы в геометрии. – М.:МЦНМО, 2005. – 56с.
- Рыбников К.А. История математики: В 2т. – Т. 1. – М., 1963. – 335с.
- Рыбников К.А. История математики: В 2т. – Т. 2. – М., 1963. – 335с.
- Савин А.П. Я познаю мир – М.: ООО “Издательство АСТ-ЛТД”, 1998. – 480с.
- Сенчишин О.Ю. Крокуючи за Піфагором // Математика в школах України. – 2005. – №2(86) – С.18-24.
- Сисоєва С.О.Основи педагогічної творчості: Підручник. – К.: Міленіум, 2006. – 344 с.
- Слєпкань З.І. Методика навчання математики. – К.: Зодіак ЕКО, 2000. – 512 с.
- Тимків Ю. Трикутні несподіванки // Математика в школах України. – 2007. – №11(411) – С.12-20.
- Тихомиров В.М. Великие математики прошлого и их великие теоремы. – М.: МЦНМО, 1999. – 24с.
- Улин Б. Цели и методы обучения математике. – М.: Народное образование. – 2006. – 336с.
- Фетисов А.И. Геометрия в задачах. Пособие для учащихся школ и классов с углубл. теоретическим и практическим изучением математики. М.: Просвещение, 1977. – 192с.
- Філіпповський Г. Пряма Ейлера, коло Ейлера і нерівність R ≥ 2r – якомога раніше // Математика в школах України. – 2004. – №14(62) – С.11-12.
- Чистяков В.Д. Старинные задачи по элементарной математике. – 3-е изд., испр.
- Шаригин И.Ф. Задачи по геометрии (планиметрия). – М.: Наука, 1982. – 160с.
- Шмигевський М.В. Видатні математики. – Харків: Вид. гр.. “Основа”, 2004. – 176с. – (Б-ка ж. “Математика в школах України”; Вип. 6(18)).
- Шклярский Д.О., Ченцов Н.Н., Яглом И.М. Избранные задачи и теоремы элементарной математики. – М., 1952. – 320с.
- Энциклопедия для детей. Т.11.Математика / Глав. Ред. Э68 М.Д. Аксенова. – М.: Аванта+, 2002. – 688с.
- Ягупов В.В. Педагогіка: Навч. посібник. – К.: Либідь, 2003. – 560с.
Список використаних комп’ютерних програм
- MS PowerPoint
- “TeachPro: Математика 7-11”
- “Открытая математика – Планиметрия 2.5. Планиметрия”
- “Уроки геометрии 8” (виробник “Кирило і Мефодій”)
- “Планиметрия” (виробник “Кудіц”)
- DG
- Windows Movie Maker
- ИКТС 1.21
1


про публікацію авторської розробки
Додати розробку

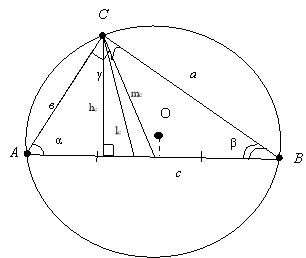
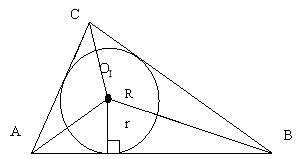
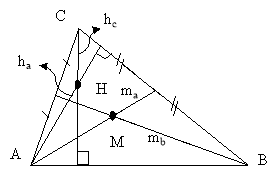
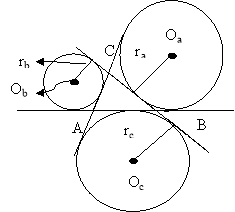
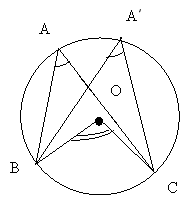
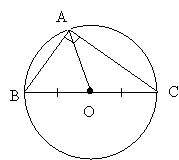
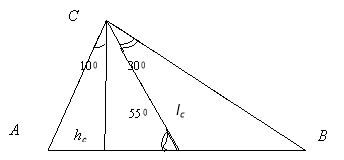
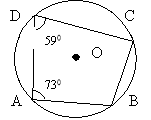
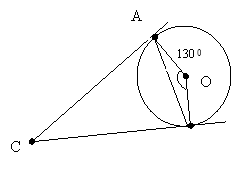
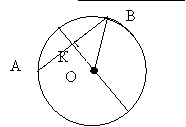

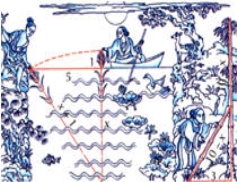
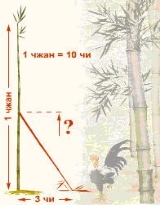
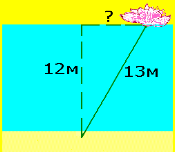
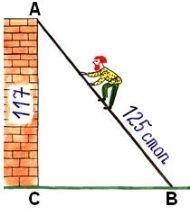
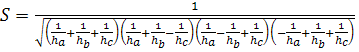




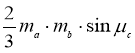
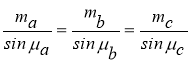
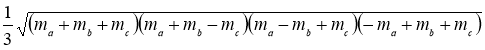
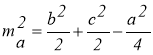 ,
, 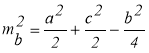 ,
,