ВИХОВАННЯ ПРАГНЕННЯ УЧНІВ ДО САМОРОЗВИТКУ ПРИ ВИВЧЕННІ ТЕМИ „ПРАВИЛЬНІ МНОГОГРАННИКИ”

Наталія ЛОСЄВА, Катерина Полозенко

ВИХОВАННЯ ПРАГНЕННЯ УЧНІВ ДО САМОРОЗВИТКУ

ПРИ ВИВЧЕННІ ТЕМИ „ПРАВИЛЬНІ МНОГОГРАННИКИ”

Основний сучасний орієнтир освіти – виховати вільну і відповідальну особистість, яка прагне саморозвитку, творчо ставиться до своєї справи і до світу в цілому. Однією з цілей вивчення геометрії є розвиток у внутрішній гармонії мислення, почуттів і волі учнів, щоб випускник школи, увійшовши в доросле життя, був здатний саморозвиватися, перетворювати навколишній світ, зважено приймати обґрунтовані рішення.

Питання саморозвитку особистості, зокрема й у навчальній діяльності на уроках математики, досліджували В. Андреєв, В. Бевз, І. Бех, Л. Виготський, В. Давидов, Л. Занков, О. Леонтьєв, Л. Петерсон, Д. Пойя, В. Роменець, С. Рубінштейн, О. Скафа, Н. Тарасенкова, В. Успенський, Р. Хмелюк та інші.

Математика загалом і геометрія зокрема мають великі можливості для вирішення різноманітних педагогічних завдань, а саме завдання саморозвитку учня, оскільки розвиває такі особистісні якості, що не виховуються засобами інших дисциплін. Особливо цінною є закладена в ній “можливість розвивати в учнів довіру до власного мислення, довіру, яка виникає завдяки досвіду внутрішньої впевненості та ясності” [7, 289].

Освітяни вже зрозуміли, що значна частина недоліків фізико-математичної підготовки школярів пов’язана з її традиційною орієнтацією на запам’ятовування певних алгоритмів дій, а не на організацію пошукової діяльності учнів. Труднощі засвоєння, на нашу думку, полягають і в тому, що учень здебільшого сприймає інформацію у готовому вигляді і механічно запам’ятовує її. Психологи ж давно довели, що знання не може бути пересаджене з голови в голову механічно, воно виникає у людини лише в результаті її власної діяльності, спрямованої як на предмет пізнання, так і на саморозвиток особистості. Учені-психологи підкреслюють, що істотними для розвитку особистості є лише знання, сконструйовані самим індивідом, а не передані від однієї людини до іншої.

Мета статті – на прикладі конкретної теми висвітлити один з можливих підходів до вивчення геометрії, який орієнтований на власне конструювання знань старшокласниками та їх саморозвиток.

Ми вважаємо, що саме такий підхід до навчання дозволяє зробити навчальний матеріал максимально наочним і доступним для багатьох учнів, подолати серйозний бар’єр між теоретичною і практичною складовими у курсі стереометрії й завдяки використанню методів моделювання суттєво вплинути не лише на конструювання знань школяра і розвиток його просторового мислення, а й на розвиток особистості.

Досвідчені педагоги знають, що завдяки певній організації навчального процесу навіть посередні учні з багатою, живою уявою можуть досягти успіхів у вивченні математики. Ми погоджуємося з думкою психологів, що мислення учнів активізується через цікавий для них матеріал і власну діяльність. Проте, підготовка і „проведення уроків діяльнісного спрямування, коли учень стає суб’єктом навчальної діяльності, є для педагогів однією з найважчих і найактуальніших проблем” [5, 8].

У цьому сенсі важливим, на нашу думку, є питання: чи готові ми спроектувати такий урок, що залучає учня до діяльності, стимулює розібратися в основах математики, зацікавлює і не потребує якихось особливих знань. Вважаємо, що суттєву роль за таких умов може відіграти звернення до конкретного, оскільки світ шкільної геометрії надає можливості постійного звернення до наочних моделей, конструювання фігур, як одного з найцікавіших шляхів створення образів плоских чи просторових геометричних фігур, накопичення практичного досвіду роботи з ними.

Розглянемо деякі аспекти уроку за темою “Правильні многогранники”, опрацьованого авторами для учнів 11-го класу. Ми визначаємо цей урок як урок відкриття нових знань, що базується на реалізації діяльнісного методу навчання й забезпечує включення учня до самостійного здобуття цих нових знань. На такому уроці відбувається  не лише відкриття нових знань, а й поглиблення вже наявних знань, творчого їх застосування, удоско­налення вмінь і навичок учня.

Підкреслимо, що при проведенні цього уроку вчитель орієнтується на вже відоме учням визначення правильного многогранника, його види та зображення. До цього уроку учням пропонується домашнє завдання, що полягає у підготовці емпатійного твору „Я – найдивовижніший правильний многогранник”. Зауважимо, що домашнє завдання надає учню можливості зробити вільний вибір многогранника, який слід описати, продемонструвати власні знання і творчі здібності, пробуджує самоповагу, надає навчанню особистісного смислу і надихає на саморозвиток особистості.

Навчальна мета: розширення понятійної бази учня за рахунок включення до неї нових елементів; узагальнення і систематизація відомостей учнів про правильні многогранники; перевірка засвоєння учнями основних даних про правильні многогранники, формування навичок моделювання правильних многогранників.

Розвивальна мета: формування здатності учня до нового способу дій; формування вміння виявляти закономірності, порівнювати, узагальнювати; розвиток логічного мислення, просторової уяви, світогляду учня; демонстрація загальнокультурного та естетичного потенціалу математики, висвітлення міждисциплінарного характеру стереометрії і взаємозв’язку теми уроку з історією розвитку людства.  

Виховна мета: розвиток самостійності і творчості; виховання активності, наполегливості, потягу до нових знань (смак нових знань); формування дослідницьких навичок і пізнавального інтересу до невідомого.

Тип уроку: урок діяльнісного спрямування і відкриття нових знань.

І. Етап самовизначення

Створюються умови включення учня до навчальної діяльності на особистісно значущому рівні: виникнення внутрішньої потреби („хочу”) і, виходячи з наявних знань, складаються орієнтири діяльності („можу”).

Умова „хочу” актуалізується у діалозі вчителя і учнів чи повідомлення педагога, наприклад, у такому вигляді.

Вступне слово вчителя. Відомі математики підкреслювали, що теорія многогранників, зокрема опуклих многогранників, є одним з найзахоплюючих розділів геометрії. І Ви в цьому переконаєтесь.

Ще піфагорійців настільки вражала краса правильних многогранників, що вони називали їх космічними тілами. Грецькою мовою слово “космос” означає “прикраса, порядок” (зверніть увагу на спільний корінь із словом “косметика”). Пізніше вчення піфагорійців про правильні многогранники виклав у своїх працях інший старогрецький учений Платон. З того часу правильні многогранники також називають платоновими тілами.

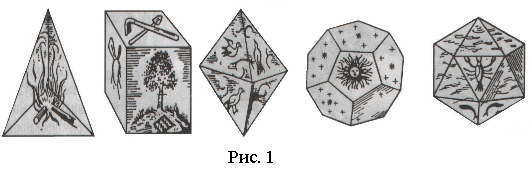Платон вважав, що світ побудований на чотирьох «стихіях» – вогонь, земля, повітря й вода, а атоми цих «стихій» мають форму чотирьох правильних многогранників. Тетраедр був втіленням вогню, оскільки його вершина спрямована вгору, як у полум'я, що розгорілося; ікосаедр – як найбільш обтічний – води; куб – найстійкіша з фігур – землі, а октаедр – повітря. П'ятий многогранник – додекаедр – символізує Всесвіт і вважається найголовнішим (рис. 1). Уже в середні віки додекаедр називали “п'ята сутність” або “квінта есенція” (латинською), звідки походить цілком сучасне слово «квінтесенція», що означає все найголовніше, дійсну сутність чогось.

Послухаємо Ваші емпатійні твори „Я – найдивовижніший правильний многогранник” (реалізується потреба учнів „хочу включитися до спільної роботи” і „можу продемонструвати власні творчі доробки”).

ІІ. Етап актуалізації знань і фіксації ускладнень у діяльності

Перевіряється домашнє завдання у вигляді емпатійного твору „Я – найдивовижніший правильний многогранник”, проводиться діалог з учнями, що готує їх до осмислення потреби у побудові нових способів дій, фіксує наявні ускладнення. На відміну від актуалізації знань традиційного уроку, де йдеться про повторення матеріалу, пройденого раніше, тут здійснюється підготовка мислення учнів до самостійної побудови нового способу дій.

Наведемо уривки з емпатійних творів учнів.

Наприклад, твір учня: “Я – додекаедр”.

Я – додекаедр (від грецького dodeka – дванадцять і hedra – грань), складений з дванадцяти правильних п'ятикутників. Отже, я маю 12 граней, 20 вершин і 30 ребер. Кожна моя вершина є вершиною трьох правильних п'ятикутників і тому сума плоских кутів при кожній вершині дорівнює 324°.

Кристал піриту (сірчистий колчедан FеS) (рис. 2), вірус поліомієліту – мої природні моделі. На мікроскопічному рівні, я та ікосаедр служимо параметрами ДНК, на якій побудовано все життя. Можна побачити також мої зв’язки з кубом, оскільки молекулу ДНК розглядають як куб, що обертається. При повороті куба послідовно на 72° за певним алгоритмом, маємо ікосаедр, який становить мою пару. Тобто, подвійна нитка спіралі ДНК побудована за принципом двосторонньої відповідності: за ікосаедром слідую я, потім знову ікосаедр, і так далі. Це обертання через куб створює молекулу ДНК.

Я – найестетичніша і найтаємничіша поверхня. Саме на моєму фоні Сальвадор Далі у картині «Тайна вечеря» зобразив Ісуса Христа зі своїми учнями (рис. 3), а також Моріс Ешер намалював мене у своїй “метаморфозі” “Рептилії” (рис. 4) [6, 219-220].

Твір “Я – ікосаедр”.

Я – ікосаедр (від грецького ico – шість і hedra – грань), складений з 20 правильних трикутників. Я маю 20 граней, 12 вершин і 30 ребер. Кожна моя вершина є вершиною п'яти правильних трикутників, і тому сума плоских кутів при кожній вершині дорівнює 300°.

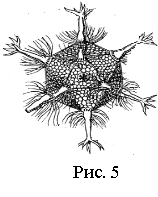
Скелет одноклітинного організму феодарії має мою форму (рис. 5) [2]. І саме я є центром дискусії біологів щодо форми вірусів. Дослідники виявили, що вірус не може бути круглим, як вважалося раніше. Щоб встановити його форму, брали різні многогранники, направляли на них світло під тими ж кутами, що й на вірус. Виявилося, що лише один многогранник має таку ж саму тінь – і це я.

Розмірковуємо разом. Учитель пропонує учням записати відомості про правильні многогранники в таблицю і проаналізувати результат (після заповнення будемо мати табл. 1).

Таблиця 1

Учні помічають, що для куба і октаедра, додекаедра та ікосаедра кількість граней і вершин змінюються місцями. Учитель пропонує пояснити такі результати.

ІІІ. Етап виявлення причин ускладнень, постановка цілей діяльності і побудова проекту виходу з ускладнень

З метою пояснення подібних “збігів” учитель пропонує учням дослідити, що відбудеться, якщо заточувати кути куба до того моменту, коли його квадратні грані перетворяться в точки?

Учнями обирається шлях подолання ускладнення, на основі обраного методу висуваються та обґрунтовуються гіпотези, використовуються моделі многогранників, а ускладнення, що виникають, долаються за допомогою нових способів дій. На цьому етапі вчителю треба добре продумати організацію діяльності учнів, він бере активну участь в обговоренні і організації процесу роботи учнів.

Підкреслимо, що принциповою відмінністю цього етапу від традиційного формулювання теми і мети заняття є осмислення учнем необхідності вирішення того чи іншого завдання, формулювання мети власної діяльності і включення до діяльності на особистісно значущому рівні. Від етапу пояснення нового матеріалу на традиційному уроці принциповою відмінністю також є те, що учні знаходять новий спосіб дій у результаті власної діяльності.

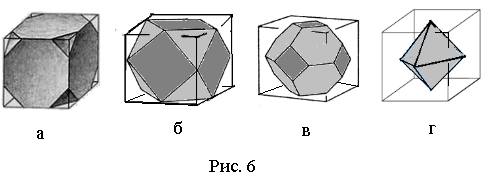
На початковому етапі заточування кутів куба виникає многогранник (рис. 6 а), який має назву зрізаний куб. Далі показані перехідні стадії (рис. 6 б,в) – мить, коли заточувальні поверхні становлять правильні трикутники і шестикутники відповідно. Ці моделі многогранників набули назви кубооктаедр і зрізаний октаедр. І остання, завершальна модель (рис. 6 г) – октаедр, шість вершин якого є центрами шести квадратних граней куба, а вісім трикутних граней отримані з восьми вершин куба.

Учитель показує заздалегідь виготовлені моделі многогранників (рис. 6 а-г). Тепер стають зрозумілими взаємозв’язки куба і октаедра, що виявилися у таблиці 1. Окрім того, учні наочно переконалися в тому, що октаедр – правильний многогранник (заточування проводилося рівномірно і симетрично).

Далі вчителем (або учнями!) пропонується розв’язати нове дослідницьке завдання: який отримаємо многогранник у результаті сточування кутів октаедра? Можливо, це буде нове платонове тіло? Уявіть, що ми заточуємо кути до тих пір, поки не залишаться лише центральні точки восьми трикутних граней. У результаті ми маємо отримати многогранник із вісьмома вершинами.

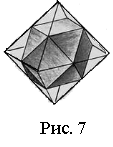
На одному із кроків заточування з’явиться вже знайомий нам многогранник (рис. 7) – кубооктаедр, тому й не дивно, що на останньому кроці з’явиться куб.

Учитель зазначає, що, мабуть, недаремно Іоганн Кеплер (1571-1630) в етюді «Про сніжинку» підкреслював, що серед правильних тіл куб є найголовнішим, початком і батьком усіх інших, а його так би мовити „дружиною” є октаедр, бо в нього стільки кутів, скільки у куба граней.

ІV. Первинне закріплення і включення у систему знань

Передбачаються типові завдання на новий спосіб дії з вербальною фіксацією властивостей, алгоритма тощо. Краще за все роботу на закріплення нових знань організувати в парах, „ланцюжку”, грі, змаганні тощо. Доцільно організувати самостійну роботу учнів із самоперевіркою за еталоном.

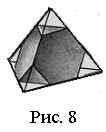Учитель пропонує учням провести аналогічне дослідження для тетраедра,  сточуючи кути тетраедра до тієї миті, поки залишаться лише центральні точки трикутних граней. На перехідній стадії матимемо модель многогранника (рис. 8) з вісьмома гранями. З них чотири грані – правильні шестикутники і чотири – правильні трикутники. Він має назву зрізаний тетраедр. Рухаючись далі, дійдемо до тетраедра, але вже “перевернутого”.

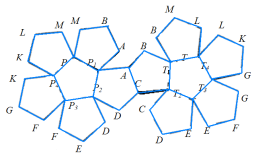
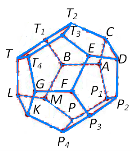
За таблицею, наступний многогранник, у якого маємо заточувати кути – ікосаедр. Дослідимо, що відбудеться, якщо заточувати ікосаедр таким чином, щоб від трикутних граней залишилися лише центральні точки. Неважко побачити, що в результаті отримаємо многогранник з 20 вершинами і 12 гранями – додекаедр, оскільки вершини грані повинні лежати у центрах п’яти трикутників, які утворюють многогранний кут ікосаедра. А це означає, що грані нового тіла мають п’ять кутів і до того ж є правильними. Вони розташовані так, щоб зустрітися по три у кожній вершині. Отже, додекаедр є спорідненим до ікосаедра у тому ж сенсі, як спорідненими один до одного є куб і октаедр. Учитель підкреслює, що такі парні правильні многогранники називаються двоїстими. Тетраедр, який під час заточування перетворювався сам у себе, називається самодвоїстим [7, 159].

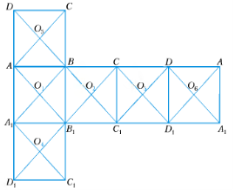
Далі вчитель зазначає, що многогранники не є об'єктами лише наукових досліджень. Їх форми – досконалі і химерні, широко використовуються в декоративному мистецтві. Чи можна виготовити ці химерні форми власними руками? Зазвичай моделі многогранників конструюють з розгорток. Пригадаємо, що поверхня многогранника розрізана по ребрах і розгорнута таким чином, щоб усі многокутники, які належать поверхні, лежали в одній площині, отримаємо фігуру, що називається розгорткою. Зауважимо, що поверхню одного й того самого многогранника можна розгорнути різними способами [6, 10].

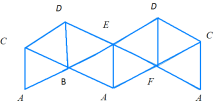
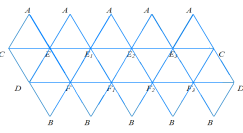
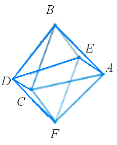
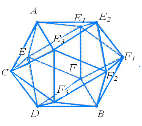
На таблиці вчитель показує можливі розгортки правильних многогранників: куба, тетраедра, октаедра, ікосаедра, додекаедра (табл.2) і пропонує учням побудувати ці моделі (учні працюють у парах, допомагаючи один одному). Після того, як клас упевниться, що дані розгортки і є розгортками правильних многогранників, розв’язується декілька типових задач.

Зазначимо, що на цьому етапі організовується комунікативна взаємодія учнів, інтеріоризація нового способу дій, самоперевірка власних рішень з еталоном, виявляються помилки, надається можливість їх виправлення, створюється ситуація успіху. Ситуація успіху сприяє формуванню в учня позитивного самовизначення на подальше навчання.

V. Рефлексія діяльності

Організується самооцінювання діяльності, фіксується ступінь відповідності результатів діяльності і поставленої мети, визначаються завдання для домашньої роботи з елементами вибору, творчості. Саме на цьому етапі всі ланки уроку поєднуються в єдину систему і виховується здатність учня до рефлексії власної діяльності.

Таблиця 2

Учитель пропонує учням оцінити результати уроку, відповісти на такі питання: Що для Вас було новим на сьогоднішньому уроці? Що найбільше зацікавило? Яка користь від конструювання моделей многогранників? Що ще хотілося б дізнатися про многогранники? Чи плануєте Ви подальшу діяльність, яка була б пов’язана з многогранниками?

Зауважимо, що для з’ясування рівня досягнення мети діяльності можна використовувати спеціальні сигнали – колір, шкала, знаки тощо.

Домашнє завдання: № 728, 733, 736, 748 [4] і № 4, 5, 9-12 [6, 18].

За бажанням учні також можуть виконати евристичні завдання. Наприклад:

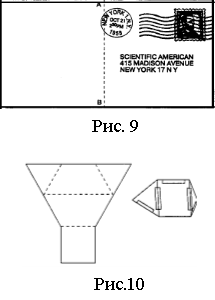
1. Яким чином розрізати заклеєний конверт (рис. 9) і скласти з нього тетраедр? [3].

2. (Головоломка). Розгортку, зображену на рис. 10 зліва, можна вирізати з пластика або щільного паперу. Зробіть дві такі розгортки. (На кресленні всі пунктирні лінії, окрім однієї, яка є довшою за інші, мають однакову довжину.) Складіть розгортку, зігнувши її за вказаними на кресленні лініями. Грані, що перетинаються між собою уздовж ребер, показаних на кресленні суцільною лінією, склейте липкою стрічкою. У результаті Ви отримаєте геометричне тіло (рис.10 справа). З двох таких тіл слід скласти тетраедр [там само].

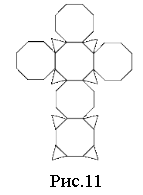
3. Побудуйте модель зрізаного куба, користуючись даною розгорткою (рис.11).

Підкреслюючи, що метою навчання є саморозвиток учнів, їх інтелект, розум, знання, здатність до їх практичного застосування, зауважимо, що ця мета є нездійсненною без інтересу учнів до навчання загалом і конкретного заняття зокрема. Каталізатором процесу пізнання завжди є інтерес, функції якого не обмежуються конкретним уроком, а стимулюють розвиток особистості, спрямовані на самовдосконалення і самореалізацію учня. Викликати інтерес до уроку нелегко, і вчителю необхідно подбати про виникнення в учня яскравих і глибоких мотивів, що потребують активних дій, допомагають долати ускладнення й рухатися впевнено до поставленої мети.  Ми погоджуємося також з думкою, що „не можна проникнути в суть геометрії, якщо не бачити краси геометричних форм, формул, тверджень” [1, 17]. Саме тому, на нашу думку, проведення уроків діяльнісного спрямування є вкрай необхідним, оскільки такі уроки дозволяють розкритися фантазії, уяві, мисленню учня, формують настанову на пошук нової інформації, актуалізують його творчий потенціал і прагнення до саморозвитку і самореалізації.

Література

1. Бевз В., Величко Л., Сверчевська І. Синергетичні принципи в освіті. Нестабільність. Відкритість // Математика в школі. – 2008. – № 4. – С. 14-17.
2. Вейль Г. Симметрия. –  М.: Наука. – 1968. – 192 с.
3. Гарднер М. Математические головоломки и развлечения. – М.: Мир. – 1999. – 447 c.
4. Геометрія: Підруч. для учнів 10‑11 кл. з поглибл. вивч. математики в серед. загальноосвіт. закладах / Г. П. Бевз, В. П. Бевз, В.М. Владіміров, Н. Г. Владімірова. – К.: Освіта. – 2000. – 239 с.
5. Кубышева М. А. Реализация технологии деятельностного метода на уроках разной целевой направленности. – М.: УМЦ «Школа 2000…». – 2005. – 32 с.
6. Лосєва Н.М. Геометричні тіла. – Донецьк: ДонНУ. – 2006. – 240с.
7. Улин Б. Цели и методы обучения математике. – М.: Народное образование. – 2006. – 336с.