контрольна робота "Перпендикулярність прямих і площин у просторі"

Контрольна робота «Перпендикулярність прямих і площин у просторі»

Варіант 1

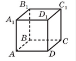1) Знайти відстань від вершини А₁ куба АВСДА₁В₁С₁Д₁ до площини ВСС₁, якщо ребро куба дорівнює 5 см.

А) 5 см  Б) см  В) 10 см

2) Площа многокутника дорівнює 20 см². Знайдіть площу ортогональної проекції цього многокутника на площину, яка утворює кут 30° із площиною многокутника. 

А) 20 см²  Б) см²  В) 10 см²  Г) см²

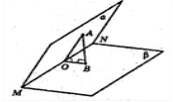3) Дано двогранний кут, міра якого 60°. AO MN, BO MN,

АВ β, АВ = 12 см. Знайдіть АО.

А) 24 см  Б) см В) см  Г) см

4) У просторі дано площину і точку А поза нею. Скільки можна провести через точку А прямих, перпендикулярних до площини ?

А) одну  Б) жодної  В) дві  Г) багато

5) З точки А до площини проведено похилі АВ і АС і перпендикуляр АМ,

АВ = 15 см, АС = 30 см. Порівняйте довжини проекцій цих похилих.

    А) МВ >МС  Б) МВ=МС  В) МВ<МС  Г) МВ=2МС

6) Із точки до площини проведено похилу АВ і перпендикуляр АО. Знайдіть АВ, якщо ВО = 6 см, АО = 8 см.

А) 6 см  Б) 7 см  В) 8 см  Г) 10 см

7) Із точки А проведено до площини α перпендикуляр АС та похилі АВ і АD. Знайдіть довжину похилої AВ, якщо ∠АВС=45⁰, АD=20 см, СD=12 см.

8) Відрізок DA – перпендикуляр до площини трикутника АВС, АВ = 10 см,

АС = 17 см, ВС = 21 см. Знайти відстань від точки D до прямої ВС, якщо відстань від точки D до площини АВС дорівнює 15 см.

9) З точки до площини проведено дві похилі, відношення яких 17:10.  Їх проекції 15 см і 6 см. Знайти відстань від точки до площини.

Контрольна робота «Перпендикулярність прямих і площин у просторі»

Варіант 2

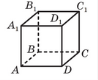
1) Знайти відстань від вершини А₁ куба АВСДА₁В₁С₁Д₁ до площини DСС₁, якщо ребро куба дорівнює 7 см.

А) 7 см  Б) см  В) 14 см

2) Знайдіть площу ортогональної проекції многокутника, площа якого дорівнює 100 см², а кут між площинами самого многокутника та його проекції 60⁰.

А) 50 см²  Б) см²  В) см²  Г) см²

3) Дано двогранний кут, міра якого 45°. AO MN, BO MN, АВ β, АВ = 12 см. Знайдіть АО.

А) 14 см       Б) см  В) см  Г) см

4) У просторі дано площину і точку А поза нею. Скільки можна провести через точку А прямих, перпендикулярних до площини ?

А) одну  Б) жодної  В) дві  Г) багато

5) З точки А до площини проведено похилі АВ і АС і перпендикуляр АМ,

АВ = 20 см, АС = 10 см. Порівняйте довжини проекцій цих похилих.

      А) МВ >МС  Б) МВ=МС  В) МВ<МС  Г) МВ=2МС

6) Із точки до площини проведено похилу АВ і перпендикуляр АО. Знайдіть ОВ, якщо АВ = 10 см, АО = 6 см.

А) 6 см   Б) 7 см   В) 8 см   Г) 10 см

7)  Із точки А проведено до площини α перпендикуляр АС та похилі АВ і АD. Знайдіть проекцію похилої AD, якщо ∠ВАС=45⁰, АВ=8 см, АD=9 см.

8) Відрізок DA – перпендикуляр до площини трикутника АВС, кут АВС = 120⁰,

АВ = 14 см. Знайдіть відстань від точки D до площини АВС, якщо ця точка віддалена від прямої ВС на см.

9) З точки до площини проведено дві похилі, відношення яких 5:6. Їх проекції 7 см і 18 см. Знайти відстань від точки до площини.