Факультативний урок .Штучні способи розв’язування рівнянь вищих степенів.

Тема:  Штучні способи розв’язування  рівнянь вищих степенів.

Мета: Ознайомити учнів з деякими штучними методами                                                              розв’язування рівнянь вищих степенів; формувати практичні            вміння та навички; розвивати вміння творчо мислити; розвивати спостережливість у процесі визначення типів рівнянь; виховувати працьовитість, культуру розумової праці; на прикладі розгляду різних методів і вправ виховувати інтерес до математики.

 

Тип: урок формування знань, умінь і навичок.

 

Обладнання: картки для індивідуальної роботи біля дошки; картки – завдання для роботи в групах.

 

Хід уроку

І. Організаційний момент.

 

ІІ. Повідомлення теми і мети уроку.

    Ми продовжуємо вивчення теми «Способи розв’язування рівнянь вищих степенів». Розв’язування будь – якої задачі є послідовним застосуванням певних знань до умови цієї задачі. Для цього потрібно добре знати і пам’ятати всі означення, правила, формули, теореми з курсу математики.

   Інколи розв’язування задачі спрощується, якщо знайти її специфічні особливості і стандартний спосіб розв’язування, розроблений для таких задач. Деякі з цих способів проілюструємо на конкретних прикладах.

ІІІ. Перевірка домашнього завдання.

а)Три учні на дошці виконують завдання, подібні до д/з.

б)Два учні працюють біля дошки з інд. завданням на повторення.

в)Індивідуальні творчі завдання сильним дітям.

 

   На уроці ми  повторимо ті способи розв’язування рівнянь вищих степенів, що вже вивчили.

а)1) (х+3)(х+1)(х+5)(х+7) = - 16

             Розв’язання:

    (х+1)(х+7)(х+3)(х+5) = - 16;

    (х²+8х+7)(х²+8х+15)= - 16;

    Заміна: х²+8х = t; тоді

    (t +7)( t+15)= - 16;

    t² + 22 t+105+16 =0;

    t² + 22 t+121 =0;

    (t +11)² = 0; t = -11;

    х² + 8х = -11

    х² + 8х +11= 0;

   Д = 64 – 44 =20;

   х_1,2= = = .

Відповідь: х_1,2= -4±√5.

 

 2) 5х⁴ -12х³ + 14х²-12х + 5 = 0;

Симетричне рівняння парного степеня, тому ділимо на х²≠0;

5х² -12х + 14 - +   = 0;

5(х² + ) -12(х+) +14=0;

Заміна х+ = t; х²+ = t²-2, маємо:

   5(t² -2)-12 t+14 = 0;

   5 t² – 10 - 12 t+14 =0;

   5 t² -12 t+4=0;

  Д = 144 –80=64;

  t _1,2= =  ;

 t₁=2; t₂=;

 а) х+ =2;                                             б) х+ = ;                                              

     х + -2=0;                                           х + -=0;                                          

   ^х/х+ -   ^х/2=0;                                      ^х/х+ -   ^х/=0;   

   =0;                                              =0;           

 (х-1)²=0;                                           Д=4-4∙5∙5<0

  х≠0;                                               розв’язків немає.

  х=1;

  х≠0;

Відповідь: х=1.

3)2(х– 1)² - 5(х – 1)(х - 2)+ 2(х– 2)² =0;

  Якщо х – 2 =0, то х-1=0, але одночасно дорівнювати нулю вони не  можуть, бо х–2=х–1; 0≠1. Отже, х – 2 ≠0.

    =0;

    =0;

    Заміна = t; 2 t²-5t+2=0,

    Д = 25-16=9     t_1,2= =  ;  t₁=2; t₂ =  ;

а) = 2;                                     б) ^2/ =^х-2/;

  – ^х-2/2= 0;                               =0;

  = 0;                                =0;

                                                                               

Відповідь: 0;3.

б) 1)розв’язати рівняння способом розкладання на множники ділення «кутом»

     х³ – 4х² +8 = 0;

    х = 2 – корінь

    х³ – 4х² +8|

  х³-2х²

     -2х²+8

     -2х²+4х

            -4х+8

            -4х+8

                    0           

(х -2)(х²- 2х-4) =0;

 х₁=2; х²- 2х-4 =0; х_2,3= = = ;

 х_2,3 =1± .

2)Розв’язати рівняння способом розкладання на множники  за допомогою схеми

   Горнера.

 х³ – 4х² + 8 = 0;

 х = 2 – корінь.

 

	1	-4	0	8
2	1	-2	-4	0

P₃ (х)

P₂ (х);     R (х) = 0.

(х-2) (х² - 2х - 4) =0;

Відповідь: 2; 1± .

в) 1.Знайти многочлен ІІІ степеня, що має корені: - 1; 2; -3.

   (х+1)(х-2)(х+3) = (х²-х-2)(х+3) = х³+3х²-х²-3х-2х-6= х³+2х²-5х-6;

  2. Знайти многочлен IV степеня, що має один двократний корінь – 1, та два простих корені 2; - 3:

   (х-1)²(х-2)(х+3) = (х²-2х+1)(х²+х - 6) = х⁴+х³-6х²-2х³-2х²+12х+х²+х - 6= х⁴-х³-7х²+13х-6.

IV. Актуалізація опорних знань.

Робота з класом – фронтальне опитування:

1. Сформулювати означення цілого раціонального рівняння п – го степеня з одним невідомим? (написати на дошці: а_пх⁴+а_п-1х^п-1+ . . .+а₁х+а₀=0)
2.  Сформулювати означення раціонального рівняння вищого степеня.
3. Що називається степенем раціонального рівняння?
4. Які способи розв’язування рівнянь вищих степенів ви знаєте?

5⁰. Алгоритм розв’язування зведеного та повного рівняння.

5. Сформулювати означення симетричного рівняння.

6. Алгоритм розв’язування симетричних рівняння.

7. Сформулювати означення кососиметричного рівняння.

8. Алгоритм розв’язування кососиметричного рівняння.

9. Які рівняння називаються однорідними?

10. Алгоритм розв’язування однорідних рівнянь.

11. Як розв’язувати рівняння №6,№5,№8 - ?

(Відповіді учнів супроводжуються поясненням алгоритму розв’язування на  прикладах рівнянь, записаних на дошці).

1. 5х⁴ - 8х³ + 9х²- 8х + 5 = 0;

2. х³ +3х² +7х +5 = 0;

3.4х⁴+ 4 х ³+ 3х² - х - 1 = 0;

4.4х⁵+ х⁴ -5 х ³- 5х² + х + 4 = 0;

5.х²  +( )² =9;

6.3х⁴ - 2х³ - 9х²- 4х + 12 = 0;

7.(2х² – 3х + 1)(2х² + 5х +1)= 9х²; (№18)

8.(х+3)(х+1)(х+5)(х+7) = - 16;

9. + + =0;                  (№31)

10. =                      (№23)

Софізм: «Усі числа рівні»

      Нехай а і в – довільні числа; а≠в;

      а-в=с; а= в+с │∙(а-в);

                а(а-в) =(в+с)(а-в);

               а²-ав=ав-в²+ас-вс;

              а²-ав-ас=ав-в²-вс;

              а(а-в-с)=в(а-в-с); │:(а-в-с)

             а=в

 Знайдіть помилку (а-в-с=0, а на 0 ділити не можна).

V. Сприйняття нового матеріалу. Проблема.

1. Запропонуйте спосіб розв’язування рівняння №7.

   (2х²-3х+1)(2х²+5х+1) = 9х².

а) перемножити многочлен на многочлен отримаємо рівняння 4 степеня;

б) зробити заміну 2х² + 1=t. Як бути з доданками -3х; 5х?

Відповідь на це запитання готувала Хандрига М.

(х + 2) (х+12) (х+3) (х+8)=4х²;

(х² +14х +24)=4х²  |:х²≠ 0;

. = 4;

(х + 14+ ) (х + 11+) = 4;

Заміна: х + = t; тоді маємо:

(t + 14) (t + 11) = 4;

t² + 25t + 154 – 4 = 0;

t² + 25t + 150 = 0;

t₁ - -10; t₂ - -15;

а) х + = -10;                                      б) х + = -15;

   х² + 10х + 24 = 0;                              х² + 15х + 24 = 0;  

х₁ = -6; х₂ = -4                                       Д = 225 – 96 = 129;

                                                                 х_3,4 = .

Відповідь: -6; -4; .

2. Запропонуйте спосіб розв’язання  рівняння:

+ =

1. Розв’язати як дробове раціональне рівняння .
2. Штучний спосіб запропонує Чубченко А.

           + = ;                            5t² + 5t – 60 = 0;

          х ≠ 0;                                                      t² + t – 12 = 0;

         + = ;

       Заміна =t;                                                        а) х + = -4;       б) х + = 3;

      ^4(t+1)/ +^4(t-4)/ + ^(t+1)(t-4)/ =0;              =0;          

    = 0;                               х₁=1; х₂=2.

                Д= 8;

                                                                                   х_1,2=         

                                                                                 х_1,2= -2±

Відповідь: 1;2; -2±.

3. Запропонуйте спосіб розв’язування рівняння виду + =А.

(обговорення способів розв’язування даного рівняння).

VI. Осмислення вивченого:

Розв’язання записати на зворотній дошці, діти розв’язують самостійно, а потім    перевіряють.

= ;

х≠0;

= ;

Заміна х+ 15/х =t, маємо:

= ;

=0;

=0;

 

;

       t₁ = 10; t₂=12.

а) х+15/х=10;                                             б) х+15/х = 12;

    х²-10х+15=0;                                              х²-12х+15=0   

Д= 100 -60 =40;                                             Д= 144 -60= 84;

Х_1,2= = 5±.                                 Х_3,4= = 6±.

Д/з. 1. Доповнити довідничок новими методами(Через 4 уроки здати довідники)

      2.   №18,№31(№23 закінчити)

        3.  Творче завдання: (ах+в)²(сх+d)(x+c) =А. Спосіб розв’язування

 

 

 

 

 

 

 

VII. Підсумок уроку (рефлексія)

      Для підведення підсумку уроку попрацюймо у групах. Кожна група одержує картку з 5 рівняннями вищих степенів. Завдання:  записати номер рівняння в такому порядку:

      1. Рівняння, що розв’язується способом розкладання на множники.

      2. Симетричне рівняння.

      3. Однорідне рівняння.

      4. Рівняння, що розв’язується способом ділення чисельника та знаменника на х≠0.

      Групи отримують картки для розкодування слова.

      Ми отримали такі ключові слова:

      Я хочу!

      Я можу!

      Я знаю!

      Я дію!

      Я це зроблю!

      А тепер дайте відповіді на такі запитання:

• Які знання,  вміння були відтворенні на початку уроку?
• Які нові знання ви набули на уроці?
• Що корисного для навчання, подальшого життя ви винесли з уроку?

      Для відповіді кожна група використає своє ключове слово. Для обдумування відповідей – 2хв.

Вчитель:  Я вірю, що все так і станеться, кожен з Вас доб’ється своєї мети.

 

 

Всім дякую за урок, до побачення.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

№ 1

1. х⁴ – 2х² - 8х - 3 = 0;
2. х⁴ + 2х²(х - 6) – 3(х – 6)² = 0;
3. = ;
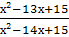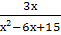4. 4х⁴ +1 2х³ - 47х²+12х +4 = 0;
5. 12х⁵ - 56х⁴ +107х³ - 107х²+56х -12 = 0;

№ 2

1. х⁴ + х ³- 8х² + 3х + 5 = 0;
2. 2х⁴ + 3х³ – 16х² +3х +2 = 0;
3. х⁴ +4х³ - 18х²-12х + 9 = 0;
4. (х² – 2х + 2)² +3х(х² – 2х +2)= 10х²
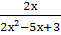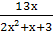5. + =6;

№ 3

1. х⁵- 7 х ³-12х² +63х + 36 = 0;
2. (х² + х +1)⁴ -3х²(х² + х +1)²+2х⁴ = 0
3. х⁴ - 2х³ –х² - 2х +1 = 0;
4. 3х⁴ - 2х³ - 9х²- 4х + 12 = 0;
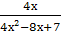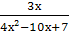5. + =1;

№ 4

1. х⁷+2х⁶ -5х⁵ -13х⁴ –13х³ - 5х² + 2х +1 = 0;
2. 4х⁴ + 4х³ - 11х²- 12х + 9 = 0;
3. 2(х²+х + 1)² – 7(х – 1)² =13(х – 1) (х²+х + 1);
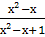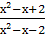4. -  =1;
5. х³ - х²-21х +45 = 0;

№ 5

1. 4х⁵+ х⁴ -5 х ³- 5х² + х + 4 = 0;
2. 2(х– 1)² - 5(х – 1)(х - 2)+ 2(х– 2)² =0;
3. х³ – х² - 4х +4 = 0;
4. 4х⁴ -16х³ + 7х²-32х + 16 = 0;
5. = ;

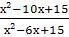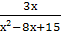№ 6

1. + =;
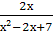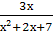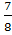2. х⁴ + х³ –х² - 7х - 6 = 0;
3. 4х⁴- 8 х ³+ 3х² - 8х + 4 = 0;
4. х² (х - 1)² +х(х² -1)=2(х+1)²;
5. 4х⁴ - 16х³ + 7х²- 32х + 16 = 0.

 

 

 

 

 

 

 

 

 

Я хочу:

• Добре знати математику;
• Знати багато способів розв’язування рівнянь;
• Поступити у вуз, тому навчаюсь в класі математичного профілю;
• Щоб набуті на уроці знання допомогли справитися із зовнішнім тестуванням.

Я можу:

• Розв’язувати рівняння вищих степенів способом  розкладання на множники, способом заміни змінних;
• Розв’язувати спеціальні типи рівнянь : симетричні, кососиметричні, зворотні, однорідні, які ми повторювали на уроці.
• Я можу поділитися цими знаннями з іншими.

Я знаю:

• Штучні способи розв’язування рівнянь вищих степенів, з якими я познайомився сьогодні на уроці;
• Що мені знадобляться набуті знання при вступі у вуз;
• Що уміння розв’язувати рівняння вищих степенів допоможуть мені при розв’язуванні інших математичних задач.

Я дію:

• Я вивчаю способи розв’язування рівнянь за підручником, в додатковій літературі, за конспектом, що дає вчитель;
• Сьогодні на уроці я вивчаю тему за повідомленнями моїх однокласників;
• Я стараюсь поглибити знання з математики.

Я це зроблю:

• Я вивчу нові способи розв’язування рівнянь;
• Я буду розвивати навики та уміння;
• Я добре напишу тематичну атестацію;
• Я справлюсь із зовнішнім тестуванням;
• Я доб’юся своєї мети.

 

 

 

 

 

 

 

 

 

 

 

 

Алгоритм розв’язування цілого раціонального рівняння з цілими коефіцієнтами

а₀хⁿ + а₁х^n-1 + а₂х^n-2 +. . . + а_n-1х +а_n = 0

1. Якщо а₀= 1, то знаходимо дільники вільного члена і перевіряємо які з них будуть коренями рівняння.

2. Якщо а₀≠1, то шукаємо корені серед нескоротних дробів , де q – дільники старшого коефіцієнта а₀, а p – дільники вільного члена а_n.

3. переходимо до рівняння нижчого степеня. Застосовуючи схему Горнера, або ділення кутом.

4. Якщо рівняння не має раціональних коренів, то розкладаємо многочлен лівої частини на множники    

     методом невизначених коефіцієнтів.

5.  Розв’язування спеціальних типів цілих раціональних рівнянь:

 а) симетричні рівняння а_n xⁿ + а_{n – 1} x^n-1 + . . . +  а₂x² +а₁x +а₀ = 0, а_n≠0 непарного степеня завжди має корінь х = -1, тому його розв’язування зводиться до розв’язування симетричного рівняння парного степеня;

б) симетричне рівняння парного степеня ділимо на х² ≠0, та робимо заміну х+ = t;

в) кососиметричне  а_n x⁴ + а_{n – 1} x^n-1 + . . . -  а₂x² - а₁x - а₀ = 0, а_n≠0 рівняння непарного степеня має корінь х=1;

г) кососиметричне рівняння парного степеня ділимо на х² ≠0 та робимо заміну х -  = t;

д) зворотне рівняння виду  а x⁴ + в x³ + сx² + dx +e = 0, де = ² ділимо на х² ≠0;

е) однорідне рівняння виду af²(x)+ bf(x)∙q(x)+cq²(x) = 0 ділимо на q² ≠0:

+ +c = 0;

Заміна = t; at²+bt+c = 0/

6. Штучні методи :

    а) рівняння виду: х² + = в.

       До обох частин рівняння додамо подвійний добуток одержимо:

       х² -  + = в - ;

       ² + – в =0;

       Заміна : =t, маємо : t²+ 2at – в = 0.

    Б) Рівняння виду :

        (ах²+ вх + с₁) (ах²+ вх + с₂) = А

        Де а≠0; в≠0.

        Заміна ах² + вх = t

        (t + c₁) (t + c₂) = А.