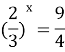Підсумковий урок "Показникові та логарифмічні функції, рівняння та нерівності"

   Показникові та логарифмічні функції, рівняння та  нерівності

Формування компетентностей:

• предметна компетентність:

сприяти узагальненню і систематизації матеріалу з теми «Показникова і логарифмічна функція, рівняння і нерівності», розвивати вміння узагальнювати, мислити логічно, робити висновки, чітко висловлювати свою думку, відтворити вміння розв’язувати завдання із даної теми;

• ключові компетентності:

- математична компетентність – розв’язувати показникові та логарифмічні рівняння та  нерівності, аналізувати особливості показникових та логарифмічних функцій, будувати і досліджувати найпростіші математичні моделі реальних об’єктів, інтерпретувати та оцінювати результати;

- спілкування державною мовою – доречно та коректно вживати математичну термінологію, поповнювати свій словниковий запас, робити висновки на основі отриманої інформації, чітко, лаконічно та зрозуміло формулювати думку;

- інформаційно – цифрова компетентність – структурувати дані, визначати достатність даних для розв’язування завдань;

- основні компетентності у природничих науках і технологіях – розпізнавати проблеми, що виникають у довкіллі, і які можна розв’язати засобами математики;

- соціальна та громадянська компетентності – співпрацювати у команді, виділяти та виконувати власну роль у командній роботі ;

- уміння вчитися впродовж життя – визначати мету навчальної діяльності, відбирати і застосовувати потрібні знання та способи діяльності для досягнення мети;

- ініціативність і підприємливість – генерувати нові шляхи розв’язання поставлених проблем, ухвалювати оптимальні рішення,  аргументувати свою позицію.

Тип уроку: урок узагальнення і систематизації знань, умінь, навичок

Обладнання: підручник, посібник, кінопроектор, ноутбук, екран, роздатковий матеріал

Хід уроку

І. Мотивація навчальної діяльності учнів, повідомлення теми, мети і завдань уроку (слайд 1,2)

На попередньому уроці ми закінчили вивчати поняття показникових і логарифмічних функцій, рівнянь і нерівностей. А сьогодні систематизуємо і узагальнимо знання по даній темі.

Знання про показникові функції, рівняння і нерівності потрібні не лише для розв’язування вправ, їх використовували багато років назад у різних сферах діяльності. А допоможе нам переконатися в цьому невеличкий блок реклами.

Реклама (слайд 3).

1. Логарифмічна функція. (слайд 4)

- К. Ціолковський вивів формулу для розрахунку абсолютної швидкості, якої досягає ракета, коли з неї витече все паливо (слайд 5-7).

- Будова слухового апарату людини відповідає властивостям цієї функції. Тому діапазон, що сприймає вухо, низький – від шелесту листя до гуркоту грому (слайд 8-11).

- Під час наповнення ставків необхідно враховувати кількість води, що прибуватиме в період повені. Розрахунки проводяться саме за допомогою цієї функції  (слайд 12-13).

- Якщо вас цікавить закон зміни роботи газу і закон зміни сили відчуття від сили збудження (психофізичний закон Вебера); закон зміни тиску від зміни висоти; тривалість хімічної реакції, зверніться до логарифмічної функції (слайд 14).

- Саме вона допоможе вам дізнатися багато цікавого навколо нас!!! (слайд 15).

2.  Логарифмічні рівняння і нерівності (слайд 16).

 Я – Логарифмічне рівняння, тобто рівняння, яке містить змінну під знаком логарифма (слайд 17).

 Розв’язуючи мене, пам’ятай, що область визначення логарифмічної функції – додатні числа, що   розглядають для а>0, а≠1 (слайд 18).

 Розв’язуючи мене, пам’ятай про методи розв’язування логарифмічних рівнянь: за означенням логарифму, за властивостями, введення нової змінної, логарифмування та графічний (слайд 19).

 Увага! Акція! Саме ці методи ти використовуєш, розв’язуючи логарифмічну нерівність, але стережись підводних рифів! Ніколи не забувай про область допустимих значень нерівності та про те, що при а>1 функція у=log_{_а} х  зростає, а при 0<а<1 – спадає (слайд 20-22).

 Якщо тобі набридло сидіти без діла, розв’язуй логарифмічні рівняння і нерівності, це є запорука успішного життя!!! (слайд 23-24).

Логарифми широка використовуються у повсякденному житті (слайд 25). Логарифми проникають і в галузь психології. Досліди показали, що організм людини ніби “логарифмує”  отримані ним подразнення, тобто величина відчуття приблизно пропорційна десятковому логарифму величини подразнення.

В астрономії гучність шуму й яскравість зірок оцінюється однаковим чином за  логарифмічною шкалою.  «Величина» зірки  являє собою  логарифм її фізичної яскравості (слайд 26). Гучність виражена в белах дорівнює десятковому логарифму відповідної фізичної величини. За логарифмічною спіраллю  закручено багато галактик, у тому числі і Сонячна система              (слайд 27).

Раковини багатьох молюсків, равликів, а також роги таких ссавців як архари (гірські кози), закручені за логарифмічною спіраллю. Можна сказати, що ця спіраль є математичним символом відношення форм росту.

 Великий німецький поет Іоганн Вольфганг Гете вважав її математичним символом життя й духовного розвитку. У соняшника зернята розташовані також за дугами, близькими до логарифмічної спіралі (слайд 28). Один з найбільш поширених павуків, епейра, сплітаючи павутину, закручує нитки навколо центра за логарифмічною спіраллю. Хіба це не цікаво?

3. Показникові рівняння і нерівності (слайд 29).

- Вони допоможуть математикам розширити область визначення показника степеня(слайд 30).

- За їх допомогою було узагальнено поняття степеня (слайд 31).

- за їх допомогою Леонард Ейлер відкрив показникові і логарифмічні кількості (слайд 32).

- Якщо ви хочете пов’язати своє життя з наукою, то вивчайте показникові рівняння і нерівності та методи їх розв’язання!

- Вам потрібно дізнатися про радіоактивний розпад?

- Ви хочете розрахувати приріст деревини?

- Вам потрібно визначити зміну атмосферного тиску? (слайд 33).

- Тоді вам до показникових рівнянь і нерівностей!!!

- Вони допоможуть вам  разв’язати багато практичних проблем (слайд 34).

4. Показникова функція (слайд 35).

- Вона допомогла людям описати такі процеси, як радіоактивний розпад, розмноження бактерій, утворення нейтронів у ланцюговій реакції, інформаційний бум (слайд 36).

- Без неї не були б розв’язані задачі на зміну атмосферного тиску, приріст деревини (слайд 37).

- І навіть сума вашого внеску до банку підлягає закону, який описує цю функцію (слайд 38).

- Ви прагнете бути активним учасником сучасного життя? Тоді докладніше вивчайте тему «Показникова функція» (слайд 39).

Отож, тема нашого уроку «Показникові та логарифмічні функції, рівняння і нерівності» (слайд 40)

 

Епіграф уроку (слайд 41)

«Знання збільшуються, а вміння вдосконалюються, коли ними ділишся!»

Оноре де Бальзак

 

ІІ. Відтворення і корекція опорних знань

1. Знайди правильну відповідь (слайд 42 - 52).

1. Функція у = 9^х називається:

А) показниковою

Б) логарифмічною

В) степеневою

2. Якщо а > 1, то функція у=25^х  на всій області визначення:

А) стала

Б) зростає

В) спадає

3. Укажіть правильну нерівність:

А) (0,7)⁶ >(0,7)^0,3

Б) ()^0,7  ()^0,9

В) 2 ⁸ > 2⁶

4. Функція у=(6х²+9)⁵   називається:

А) показниковою

Б) лінійною

В) степеневою

5. Функція у =    називається:

А) тригонометричною

Б) логарифмічною

В) степеневою 

6. Яка з наведених рівностей є основною логарифмічною тотожністю:

А)

Б)

В) = p

7. Логарифм добутку двох додатних множників дорівнює:

А) добутку логарифмів множників

Б) сумі логарифмів множників

В) різниці логарифмів множників

8. Логарифм частки двох додатних чисел дорівнює:

А) добутку логарифмів множників

Б) сумі логарифмів множників

В) різниці логарифмів діленого і дільника

9. Значення виразу         дорівнює:

А) 22

Б) 18

В) 20

10. Укажіть область визначення функції у=

А) (-3;5)

Б) (- ∞;-3) U (5;+∞)

В) (5;+∞)

К л ю ч

 

1	А	6	Б
2	Б	7	Б
3	В	8	В
4	В	9	А
5	Б	10	А

 

2. Бліц – опитування (слайд 53 - 54).

1. Якою є область визначення  показникової функції?

(множина всіх дійсних чисел)

2. Якою є область значень показникової функції?

(область значень показникової функції є всі додатні числа)

3. При якій умові  показникова функція спадає?

(показникові функція спадає, якщо основа лежить в межах від 0 до 1)

4. У якій точці графік показникової функції перетинає вісь ординат?

(0;1)

5. Як називається показникова функція в математиці та багатьох прикладних науках?

(експонента)

6. Яким є графік логарифмічної функції по відношенню до графіка показникової функції?

(симетричний йому відносно бісектриси першого координатного кута)

7. При якій умові логарифмічна функція зростає?

(якщо основа логарифма набуває значень, більших за 1)

8. В якій точці графік логарифмічної функції перетинає вісь ординат?

(графік не перетинає вісь ординат, бо підлогарифмічний вираз не можу бути рівний нулю)

ІІІ. Повторення і аналіз основних фактів, подій, явищ.

3. Знайди відповідність (слайд 55 - 56).

1. аm∙ аn  + 3. 4. аm: аn 5. 6. (аm)n 7. 8. (a b) n 9. а1 10. ( 11. 12. а-n 13. 14. а0

А.  аmn Б.  аm-n В.  an bn Г.  аm+n Д. Е. - Є.  Ж. у З. И.  1 І.    0 Ї.    b Й.  а К.

 

К л ю ч

 

1	Г	8	В
2	Ж	9	Й
3	З	10	Є
4	Б	11	Ї
5	Е	12	К
6	А	13	І
7	Д	14	И

 

4. Знайди помилку (слайд 57 - 61).

1. На рисунку зображено графік функції у=

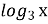
(Якщо основа логарифма більша за 1, то графік функції буде зростати).

2. 

.

: .

(Якщо основа показникової функції лежить в межах від 0 до 1, то, опускаючи основу, знак нерівності змінюємо на протилежний).

3. 

 х              

Відповідь:.

(Не враховано ОДЗ, тоді х є (0;36)).

4. 

    х=4.

Відповідь: 4.

(Щоб подати дріб за основою 2, потрібно поставити показник степеня  -4).

5.  .

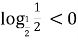(Логарифм, у якого основа і під логарифмічний вираз дорівнюють одному і тому самому числу, дорівнює 1, а 1 не може бути меншою за 0).

 

ІУ. Повторення, узагальнення і систематизація понять, засвоєння відповідної системи знань, провідних ідей і основних теорій.

5. Наздожени лідера (індивідуальна робота за рівнями) (слайд 62 - 63).

а) > 81,

 б) - 8 + 7 =0,

 в) - <15,

г) = ,

д)

 е) ,

є)

ж) .

Перевір сусіда (учні обмінюються зошитами , перевіряють і оцінюють роботу один одного)

а) х є

б) 1 ; 0

в) х є

г) – 2

д) х є

е) 6; - 3

є) х є

ж) 0,0001 ;  10

 

6. Розв’язок біля дошки ( 1 учень з кожної групи) (слайд 64).

Розв’язати рівняння:

,

3^х+3+3^х+4+3^х+5=13 ,

Розв’язати нерівність:

2^х+3+ 10 11^х+2 11^х+3+ 2^х+2,

1+.

 

7. Доміно (слайд 65).

 

			2
	3		9
2х=32	0	ех=е	5
	1
-4	lg1000	3
12		25	3х=81
4		-2

 

У. Підсумок уроку

     8. Показниково – логарифмічний вінегрет (слайд 66 - 67).

Розділити на 2 колонки способи розв’язання показникових та логарифмічних рівнянь

1. За означенням

2. Зведення до спільної основи

3. Приведення рівняння до квадратного

4. За властивостями

5. Введення нової змінної

6. Логарифмування

7. Графічний

8. Зведення до спільного показника

9. Винесення спільного множника за дужки

 

Перевір себе

Показникові 1.Зведення до спільної основи 2. Зведення до спільного показника 3. Винесення спільного  множника за дужки 4. Приведення рівняння до квадратного 5. Графічний

Логарифмічні      1.За означенням      2.За властивостями      3. Введення нової  змінної       4. Графічний       5.Логарифмування

 

8. Заморочки з бочки (слайд 68).

1. Хто винайшов логарифми?                (Непер)

2. Яку назву має графік логарифмічної функції?   (логарифміка)

3. Коли таблиці логарифмів були перекладені на російську мову?           (в 1703 році)

4. Із зазначених функцій назвіть логарифмічні і показникові?

1)  у=4х 2)у=3)у= 

4) у= 5)у==+

(логарифмічна  -  3,  показникова – 4)

5. Обчислити

(-5)

6. Який графік є графіком функції у=

(г)

 

 

 

 

 

УІ. Домашнє завдання (слайд 69  - 71).

Рівень А  №87, №94, №174 (а,в)

Рівень Б  №91, №103, №183

Рівень В  № 111, №115 (а, г), №191

 

Використані джерела.

1. https://svitppt.com.ua/algebra/logarifmichna-funkciya-ii-grafik-ta-vlastivosti.html
2. https://naurok.com.ua/prezentaciya-na-temu-algebra-11-klas-logarifmichna-funkciya-v-zhitti-lyudini-14438.html
3. Математика . Шкільний світ. №14 (266) 2004 р. ст..7-10.
4. Математика . Шкільний світ. №44 (344) 2005 р. ст..10-12.
5. Математика . Шкільний світ. №7 (403) 2007 р. ст..15-17.
6. Математика . Шкільний світ. №15 (459) 2008 р. ст..11-14.
7. Математика . Шкільний світ. №7 (547) 2010 р. ст..6-15.
8. Математика . Шкільний світ. №18 (606) 2011 р. ст..15-17.