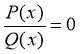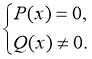Рівняння, що зводяться до квадратних

Тема. Рівняння, що зводяться до квадратних

Мета: засвоєння учнями основних видів цілих рівнянь, розв'язан­ня яких зводиться до розв'язування квадратних рівнянь, та схем їх роз­в'язування; сформувати вміння виділяти вивчені види рівнянь серед інших рівнянь, а також використовувати відомі схеми для розв'язуван­ня названих видів рівнянь.

Тип уроку: засвоєння знань та вмінь.

Наочність та обладнання: опорний конспект «Рівняння, що зво­дяться до квадратних».

Хід уроку

I. Організаційний стан

II. Перевірка домашнього завдання

Оскільки завдання домашньої роботи були такого самого типу, як і вправи класної роботи, то під час перевірки приділяємо увагу лише завданням підвищеної складності (традиційно це завдання на розкла­дання виразів вищих степенів на множники, у розв'язуванні яких ви­користовується прийом заміни змінних).

ІІІ. Формулювання мети і завдань уроку

Вчитель ще раз нагадує учням про те, що вміння розв'язувати квад­ратні рівняння є одним із найважливіших для подальшого вивчення не тільки алгебри, але й багатьох суміжних дисциплін. Так, тема цілком присвячена вивченню питання про сферу застосування набутих умінь під час розв'язування завдань, передбачених програмою з математики у 8 класі.

На цьому уроці буде вивчено питання про застосування вмінь розв'я­зувати квадратні рівняння в розв'язуванні деяких інших видів рівнянь.

IV. Актуалізація опорних знань та вмінь

 З метою успішного сприйняття учнями навчального матеріалу уроку слід активізувати такі знання і вміння: застосовувати основні поняття, пов'язані з поняттям рівняння з однією змін­ною; виконання арифметичних дій з дійсними числами; алго­ритм розв'язання найпростіших дробово-раціональних рів­нянь; застосування різних способів розв'язання квадратних рівнянь різних видів.

Виконання усних вправ

1. Скоротіть дроби:

; ; ; ; ; .

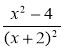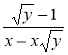2. Знайдіть корені рівнянь:

х² – 64 = 0; у² + 49 = 0; 2р² – 7р = 0; т² = 0; 2х² + 4х – 1 = 0; х² + 3х + 4 = 0.

3. При яких значеннях змінної х вираз 3х – 1 набуває значень: 0; -2; 3; ?
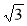4. Виконайте множення:

(x + 1)(x – 1); (x + 1)(x – 3); (x + 1)(x + 2); (x – 1)(x – 4).

V. Засвоєння знань

План вивчення нового матеріалу

1. Приклади рівнянь, що зводяться до квадратних шляхом уведен­ня нової змінної (заміною змінних). Як розв'язувати такі рів­няння?
2. Яке рівняння називають біквадратним рівнянням? Як розв'язати біквадратне рівняння?
3. *Як розв'язати рівняння виду

(х + а)(х + b)(х + с)(х + d) = A,

де a + d = b + c?

 Програмою з математики в розділі «Рівняння, що зводяться до квадратних» передбачено вивчення способів розв'язування цілих рівнянь, що зводяться до квадратних шляхом введення нової змінної, а також дробово-раціональних рівнянь.

На уроці проводиться ознайомлення учнів із загальною схемою розв'язання рівнянь, що перетворюються на квадратні шляхом введен­ня нової змінної. Якщо на попередньому уроці учні добре засвоїли прийом переходу до нової змінної у ході розкладання виразів на множ­ники, то на цьому уроці в учнів не повинно бути проблем із ро­зумінням схеми розв'язування рівнянь шляхом уведення нової змін­ної – схема розв'язування рівнянь таким методом майже співпадає зі схемою перетворення виразів (додається один пункт – після виконан­ня оберненої заміни розв'язати здобуте рівняння).

Що стосується біквадратних рівнянь, то їх можна розглядати як особ­ливий випадок рівнянь, що були розглянуті вище, тому слід зауважити, що складена вище схема використовується і під час розв'язування цих рівнянь (можна наголосити на тому, що, на відміну від інших подібних рівнянь, у біквадратних рівняннях завжди «спрацьовує» заміна х² = t).

Якщо учні мають високий рівень навчальних досягнень, їх можна ознайомити зі способом перетворення рівнянь виду

(х + a)(х + b)(х + с)(х + d) = А,

де a + d = b + c, до рівнянь виду аР²(х) + bР(х) + с = 0, де Р(х) – многоч­лен від однієї змінної, з тим, щоб потім розв'язати утворене рівняння розглянутим вище способом.

VI. Формування вмінь

Виконання усних вправ

1. Яку заміну слід виконати в рівнянні, щоб дістати квадратне рівняння:
   а) (х² + 6х + 9) – 2(х + 3) – 3 = 0; б) (х² + 6х + 9)² – 2(х + 3)² – 3 = 0;

в) (х² + 6х)² – 2(х² + 6х) – 3 = 0.

2. Які квадратні рівняння дістанемо в завданні 1, якщо виконаємо
   відповідну заміну?

Виконання письмових вправ

Для реалізації дидактичної мсти уроку слід розв'язати завдання та­кого змісту:

1. Розв'язування рівнянь різного виду, що зводяться до квадратних уведенням нової змінної. Розв'яжіть рівняння:

а) (х² – 1)² – 11(х² – 1) + 24 = 0; б) (х² + 2х)² – 2(х² + 2х) – 3 = 0.

2. Розв'язування біквадратних рівнянь.

Розв'яжіть рівняння: а) 2х⁴ – 9х² + 4 = 0; б) 36х⁴ – 7х² – 4 = 0.

3. Логічні вправи та завдання підвищеного рівня складності для учнів,
   які мають достатній та високий рівні знань.

1) Розв'яжіть рівняння:

а) (х² + 5х)(х² + 5х – 2) = 24; б) (2х² + х + 1)(2х² + х + 3) = 8;

в) (х² – 5х + 7)² – (х – 2)(х – 3) = 1; г) (х – 1)(х – 2)(х – 3)(х – 4) = 120;

д) (x – 1)x(x + 1)(x + 2) = 24; e) (х + 3)²(х + 2)(х + 4) = 12.

2) Розв'яжіть рівняння: а) ; б) .

3) Розв'яжіть рівняння: а) х – 6 + 5 = 0; б) х + – 6 = 0;

в) ; г) ; д) ;

є) .

4) Знайдіть пропущений вираз:

4. На повторення: завдання на перетворення раціональних виразів; на розв'язування дробових рівнянь (такого рівня складності, як було розв'язано в темі «Раціональні вирази»).

 У ході розв'язування письмових вправ на відпрацювання вмінь застосовувати схему, що передбачає введення нової змінної для переходу від даного рівняння до квадратного, слід вимагати від учнів урахування кількох важливих моментів:

• якщо вводити заміну то тільки ефективну (щоб у результаті переходу до нової змінної рівняння з неквадратного перетворилось на квадратне);
• розв'язувати новоутворене квадратне рівняння відносно його змінної (типова помилка учнів - виконання подібних записів: t² + 4t + 3 = 0,

х₁ = -1, х₂ = -3);

• обов'язковим етапом розв'язування рівняння шляхом введення но­вої змінної є виконання оберненої заміни (звісно, у випадку, коли рівняння, здобуте після заміни, має корені).

Вправи на повторення є підготовчими до сприйняття матеріалу на­ступного уроку.

VII. Підсумки уроку

В якому випадку правильно виконано записи?

а) х⁴ – 3х² + 2 = 0. Заміна: х² = t, х⁴ = t², тоді t² – 3t + 2 = 0; x₁ = 1, х₂ = 2.

Відповідь. 1; 2.

б) х⁴ – 3х² + 2 = 0. Заміна: х² = t, х⁴ = t², тоді t² – 3t + 2 = 0, t₁ = 1, t₂ = 2.

Обернена заміна: х² = 1 або х² = 2, маємо: х₁ = 1, х₂ = .

Відповідь. 1; .

в) х⁴ – 3х² + 2 = 0. Заміна: х² = t (t ≥ 0), тоді t² – 3t + 2 = 0; t₁ = 1, t₂ = 2;

обернена заміна: х² = 1 або х² = 2, маємо: х = ±1, х = .

Відповідь. ±1; .

VIII. Домашнє завдання

1. Вивчити схеми розв'язання рівнянь, що зводяться до квадратних уведенням нової змінної.
2. Розв'язати вправи на застосування вивченої схеми.
3. На повторення: завдання на перетворення раціональних виразів; на розв'язування дробових рівнянь (такого рівня складності, як було розв'язано під час вивчення теми «Раціональні вирази»).