Квадратний тричлен та його корені. Розкладання квадратного тричлена на лінійні множники

Тема. Квадратний тричлен та його корені. Розкладання квадратного тричлена на лінійні множники

Мета: домогтися засвоєння учнями означення квадратного три­члена та його коренів, а також формулу розкладання квадратного тричлена на лінійні множники; сформувати вміння відтворювати вив­чені означення і формули та використовувати їх для розв'язування за­вдань на знаходження коренів квадратного тричлена, розкладання квадратного тричлена на лінійні множники.

Тип уроку: засвоєння знань та вмінь.

Наочність та обладнання: опорний конспект «Квадратний тричлен».

Хід уроку

I. Організаційний етап

На цьому етапі уроку слід надати учням інформацію про:

• орієнтовний план вивчення розділу;
• кількість навчальних годин;
• приблизний зміст матеріалу;
• основні вимоги до знань та вмінь учнів;
• приблизний зміст завдань, що будуть винесені на контроль.

(Цю інформацію можна помістити на стенді «Довідково-інфор­маційний куточок» у кабінеті математики та для економії часу запро­понувати учням для самостійного ознайомлення у позаурочний час).

II. Перевірка домашнього завдання

Зібрати зошити учнів на перевірку якості виконання аналізу кон­трольної роботи.

III. Формулювання мети і завдань уроку

Вчитель повідомляє учням про те, то вміння розв'язувати квадрат­ні рівняння є одним із найважливіших для подальшого вивчення не тільки алгебри, але й багатьох суміжних дисциплін. Так, тема цілком присвячена вивченню питання про сферу застосування вмінь розв'язу­вати квадратні рівняння під час виконання завдань, передбачених про­грамою з математики у 8 класі.

Метою цього і наступного уроків є вивчення способу застосування квадратного рівняння для розкладання многочленів на множники.

IV. Актуалізація опорних знань та вмінь

 З метою успішного сприйняття учнями навчального матеріалу слід активізувати такі знання і вміння учнів: виконання ариф­метичних дій з раціональними числами; виконання арифме­тичних дій з раціональними виразами; застосування різних способів та прийомів розв'язання квадратних рівнянь різних видів.

Виконання усних вправ

1. Розкладіть на множники вираз:  а) х² – 144; б) 7 – у²; в) а³ + 2а² +а;

г) т³ + 1; д) b² – 10b + 25; е) b² – а² + b – а; ж) (m – 1)² – 4.

2. Чи має квадратне рівняння корені? Якщо має, то скільки:
   a) x² – 2x + 1 = 0; б) x² – 5 = 0; в) х² + 1 = 0; г) 3x – x² = 0.

V. Засвоєння знань

План вивчення нового матеріалу

1. Що таке квадратний тричлен?
2. Що називається коренем квадратного тричлена? Як знайти всі ко­рені квадратного тричлена?
3. За якою формулою можна розкласти квадратний тричлен на множни­ки? Які дії слід виконати, щоб розкласти даний квадратний тричлен на лінійні множники (якщо це можливо на множині дійсних чисел)?

 Вивчаючи матеріал уроку за поданим планом, учні мають засвої­ти означення квадратного тричлена та вміти відрізняти його се­ред інших виразів, а також наводити свої приклади квадратних тричленів (цьому сприяє виконання відповідних усних вправ).

Крім того, учні мають усвідомити, що задача про відшукання ко­ренів квадратного тричлена зводиться до розв'язування відповідного квадратного рівняння (тому перед вивченням теми слід організувати повторення матеріалу, пов'язаного з розв'язуванням квадратного рів­няння — див. етап актуалізації...). Слід підкреслити, що розкладання квадратного тричлена на лінійні множники за формулою є ще одним зі способів розкладання многочленів на множники, який широко засто­совується в курсі алгебри.

Учні мають знати означення квадратного тричлена, означення ко­реня квадратного тричлена, формулу розкладання квадратного тричле­на на лінійні множники. Усвідомленому сприйняттю учнями нового матеріалу може сприяти інтерактивна форма запису конспекту уроку: у вигляді діалогу — питання – відповідь.

VI. Формування вмінь

Виконання усних вправ

1. Чи є число 1; 0; 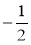коренем квадратного тричлена:

а) 2х² – 5х + 3; б) ; в) х² – х?

2. Доведіть, що квадратний тричлен х² + 2 не має коренів.
3. Чи має квадратний тричлен корені і якщо має, то скільки:

а) х² + 2х + 1; б) х² + 5; в) х² – 1; г) -3х + х²?

4. Відомо, що а — перший коефіцієнт, a х₁ і х₂ — корені деякого квадратного тричлена. Подайте тричлен у вигляді добутку, якщо:

а) а = 1; х₁ = 2; х₂ = -3; б) а =3; ; .

Виконання письмових вправ

Для реалізації дидактичної мети уроку слід розв'язати завдання та­кого змісту:

1. Знаходження коренів квадратного тричлена.
   Знайдіть корені квадратного тричлена:

а) x² + х – 12; б) х² – 2х – 35; в) 3х² + 16х + 5; г) 7х² – 96х – 28;

д) х² – 10х + 18; є) 16х² + 24х + 3; ж) 4х² – 28х + 49; з) х² + 3х + 5.

2. Знаходження кількості коренів квадратного тричлена.
3. Розкладання на множники квадратного тричлен. Чи можна роз­класти на лінійні множники квадратний тричлен?

1) Розкладіть на множники квадратний тричлен:

а) а² – 13а + 22; б) -b² + 2b + 24; в) 100с² – 50c + 6; г) ;

д) ; е) т² – 6m – 1; ж) 4х² – 20х + 25; з) -3х² + 7х – 5.

2) При яких значеннях а можна розкласти на лінійні множники квадратний тричлен:

а) 2х² + 7х – а; б) ах² + 4х + 8; в) 3х² – 5ах – 1; г) (a – 1)х² + 6ах + 6?

4. Логічні вправи та завдання підвищеного рівня складності для учнів, які мають достатній та високий рівні знань.

1) Розкладіть на множники тричлен:

а) х² – 2ху + 63у²; б) 2а² + 7аb + 3b²; в) 3m² +11тп – 4п².

2) Знайдіть пропущений вираз:

5. На повторення: виділити квадрат двочлена з виразу.

 Розв'язування завдань на знаходження коренів, дослідження існування коренів квадратного тричлена зводиться до розв'язу­вання відповідного квадратного рівняння (відповідні відомості активізовано на етапі актуалізації). Перед розв'язуванням за­вдань, що вимагають розкладання квадратного тричлена на лінійні множники, доречно спочатку з'ясувати, чи можливе воно, тобто визначити знак дискримінанта квадратного три­члена, і тільки після цього виконувати розкладання на множ­ники, якщо воно можливе.

Завдання на повторення має на меті підготувати учнів до сприй­няття деяких властивостей квадратного тричлена, про які мова піде на­ступного уроку.

VII. Підсумки уроку

Укажіть правильну відповідь.

1) Корінь тричлена 3х² – 13х +4: а) 4; ; б) ; 4; в) 1; 12; г) - 1; - 12.

2) Розклад тричлена 3х² – 13х + 4 на лінійні множники має вигляд:

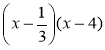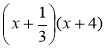а) ; б) ; в) 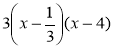; г) (3х – 1)(х + 4).

VIII. Домашнє завдання

1. Вивчити зміст основних нових понять, вміти відповідати на запи­тання (див. конспект).
2. Розв'язати вправи на знаходження коренів квадратного тричлена та на розкладання квадратного тричлена на лінійні множники.
3. На повторення: теорема Вієта та обернена теорема, їх застосування для розв'язування квадратних рівнянь; розв'язати завдання на виді­лення повного квадрата.