Формули з алгебри для підготовки до ЗНО
|
|
|
Основна властивість дробу |
|
1. Якщо
|
|
Приклад. Скоротити дріб |
|
Розв'язання |
|
1) Розкладемо чисельник і знаменник дробу на множники: |
|
2) Поділимо чисельник і знаменник здобутого дробу на спільний множник (а+ 3); маємо:
Отже: |
|
2. Якщо
|
|
Приклад. Скоротити дріб |
|
1) Розкладемо чисельник і знаменник раціонального дробу на множники:
|
|
2) Помітивши, що (3 – с) і (с – 3) — протилежні вирази, скористаємось правилом знаків: поміняємо, знак перед дробом, і наприклад, знак множника
(3 –с) у чисельнику: |
|
3) Скоротивши даний дріб на спільний множник чисельника і знаменника (с–3); маємо: |
|
Отже, |
|
3. Якщо
Приклад. Звести дріб |
|
Розв'язання |
|
1) Розкладемо новий знаменник на множники: х(х+у). 2) Знайдемо додатковий множник; для цього новий знаменник поділимо на знаменник даного дробу.
3) Помножимо чисельник і знаменник даного дробу на х (додатковий множник): |
|
Конспект 4 |
||
|
Множення і ділення раціональних дробів |
||
|
|
1. Для будь-яких А, В,С і D де В ≠ 0, D≠ 0, справджується рівність:
|
|
|
|
||
|
|
2. Для будь-яких А і В, В≠ 0, справджується рівність:
|
|
|
|
||
|
|
3. Для будь-яких А, В, С і D де B ≠ 0,C≠ 0, D ≠ 0, справджується рівність: |
|
|
Зауваження. Дріб, яким записується добуток або частка дробів необхідно (якщо це можливо) скоротити! Записувати його раціональним дробом — тільки виходячи з умови завдання |
||
|
Конспект 5 |
|
Тотожні перетворення раціональних виразів |
а) встановлюємо (визначаємо), які дії з раціональними дробами слід виконати, виходячи з умови завдання; б) виконуємо ці дії або у порядку спадання дії, або користуючись законами(властивостями) арифметичних дій (перестановка + і; сполучна + і; розподільна) та властивостями раціональних дробів (основною властивістю дробу) |
|
|
Конспект 7 |
|
|
|
Степінь з цілим від'ємним показником. Стандартний вигляд числа |
|
|
1 |
Якщо п— натуральне число (п > 2) і а — будь-яке число, то
Зауваження: a1 = a, 1n = 1, 0n = 0 для будь-якого а |
|
|
|
|
|
|
2 |
Якщо п — ціле від'ємне (протилежне натуральному числу) і а ≠ 0, то Зауваження:a0 = 1, для а ≠ 0 |
|
|
|
|
|
|
Конспект 8 |
|
|
Функції |
|
|
1. Числова функція — замість змінної .у від змінної х, за якої кожному значенню змінної х з деякої множини (область визначення функції) відповідає єдине значення vз деякої множини (область значень функції). х — аргумент; у — функція (значення функції). |
|
|
2. Найчастіше функції задають формулами. |
|
|
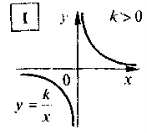
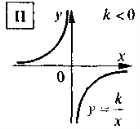
3. Функція виду (задана формулою) |
|
|
4. Властивості функції а) область визначення: х ≠ 0; б) множина значень: у≠ 0; в) графік — гіпербола — крива, що складається із двох частин (віток), симетричних відносно (0;0): |
|
|
|
|
|
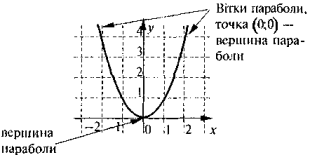
5. Функція у = х2мас такі властивості:
а)область визначення: б)множина значень: у ≥ 0: (у — невід'ємне число); в) графік — парабола. |
|
|
Конспект 9 |
|
Арифметичний квадратний корінь і його властивості |
|
1. Означення: |
|
а) якщо число х с коренем рівняння х2= а,тох — квадратний корінь з числа а: |
|
б) якщо число х ≥ 0 є коренем рівняння х2= а, то х — арифметичний квадратний корінь х числа а. |
|
Записують: |
|
Запам'ятай! Запис |
|
2. Властивості. Якщо а ≥ 0, b ≥ 0, то справджується рівність: |
|
а) |
|
б) якщо а ≥0 і b>0, то |
|
в) для будь-яких а: |
|
г) |
|
3. Застосування |
|
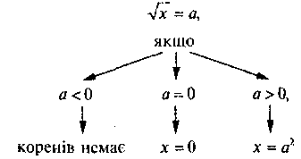
а) Розв'язування рівняння |
|
|
|
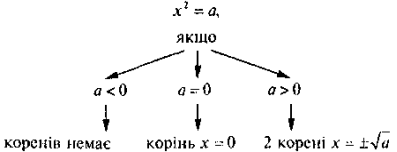
б) Розв'язування рівняння х2= а: |
|
|
|
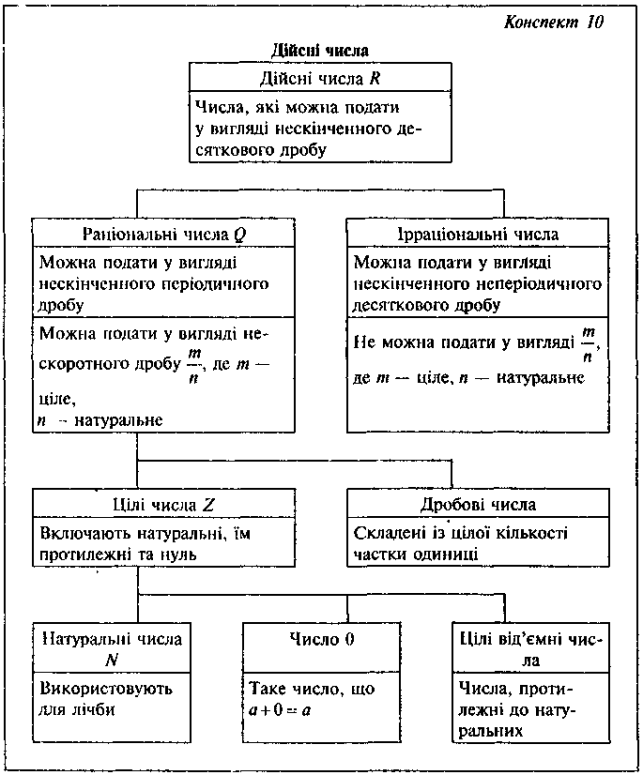
Конспект 11 |
||
|
Перетворення ірраціональних виразів |
||
|
1. Винесення множника з-під знака кореня. |
||
|
|
Якщо b ≥ 0, то |
|
|
2. Внесення множника під знак кореня. |
||
|
|
Якщо b≥ 0, то |
|
|
3. Арифметичні дії з виразами, що містять арифметичний квадратнийкорінь. |
||
|
а) Алгебраїчне додавання: |
||
|
б) множення: |
||
|
|
||
|
|
||
|
в) ділення: |
||
|
г) позбавлення від ірраціональності в знаменнику дробу: |
||
|
|
||
|
Конспект 12 |
||||||||
|
Квадратні рівняння |
||||||||
|
1. Означення: |
||||||||
|
|
ах2 + bх + с=0, а ≠0, bі с — будь-які дійсні числа |
|
||||||
|
↓ Квадратні рівняння 2. Види квадратних рівнянь: |
||||||||
|
|
Неповні квадратні рівняння: |
|
||||||
|
|
b = 0,ах2 + с=0 |
c=0,ax2 + bx=0 |
с = b = 0,ах2=0 |
|
||||
|
Якщо b = 0 або с = 0 або b= с = 0 ↑ |
||||||||
|
|
ах2 + bx + c =0, а ≠ 0 |
|
||||||
|
↓ Якщо а = 1 |
||||||||
|
|
Зведене квадратне рівняння |
|
||||||
|
|
х2 + px+q=0 |
|
||||||
|
|
||||||||
|
|
Конспект 13 Теорема Вієта |
||||
|
1. |
Для зведеного квадратного рівняння: |
||||
|
|
Якщо х2 + рх + q= 0 має корені х1 і х2(D>0), то |
|
|||
|
|
|
|
|||
|
|
х1 +х2 = -р;х1· х2 =q |
|
|||
|
2. |
Для квадратних рівнянь загального вигляду: |
|
|||
|
|
Якщо ах2 + Ьх + с =0 має корені х, і х2(D>0), то |
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
3. Обернена теорема: |
|||||
|
|
Якщо числа т і п такі, що m + n = -p,mn = q, то |
|
|||
|
|
|||||
|
|
тіп — корені рівняння х2+ pх + q=0 |
|
|||
|
4. Застосування: |
|||||
|
а) розв'язування зведених квадратних рівнянь «підбором»? |
|||||
|
х2 – 2х– 3=0:
х1 + х2 = 2, х1 · х2 = -3 |
|||||
|
б) розв'язування рівнянь ах2 + bх +с = 0,де |
|||||
|
|
а + с= b, |
|
а + с= - b, |
|
|
|
|
|
|
|
|
|
|
|
x1 = -1, |
|
x1 = 1, |
|
|
|
|
3х2 + 2х–1=0, 3–1= 2,
х1 =-1, |
|
3х2–2х–1=0, 3–1= 2 =-(-2),
х1 =1, |
|
|
|
|
Конспект |
||||
|
1. |
Квадратний тричлен Означення: |
||||
|
|
ах2 + bх + с, а ≠ 0 |
— квадратний тричлен |
|
||
|
2. |
Корені квадратного тричлена: |
|
|||
|
|
якщо х таке, що ах2 + bх + с = 0, то |
|
|||
|
|
|
|
|||
|
|
х — корінь квадратного тричлена ах2 + bх + с |
|
|||
|
3. |
Розкладання квадратного тричлена на лінійні множники: |
|
|||
|
|
якщо x1і х2 — корені тричлена ах2 + bх + с, то |
|
|||
|
|
|
|
|||
|
|
ах2+ bx + c= а(х–х1)(х–х2) |
|
|||
|
|
|
|
|||
|
1. |
Конспект Рівняння, що зводяться до квадратних Шляхом виконання заміни змінних: |
|
|
a) |
У рівнянні аР2n(х) + bРn(х) + с = 0, де а ≠ 0, |
|
|
|
Р(х)— многочлен від змінної х |
|
|
|
Заміна: Рn(х)=t(t≥ 0), тоді Р2n(х)=t2, |
|
|
|
тоді |
|
|
|
аР2n(х) + bРп(х)с=0 |
|
|
|
Особливий випадок: |
|
|
|
ах4 + bх2+ с = 0 — біквадратне рівняння |
|
|
|
Заміна: х2=t (t≥ 0) |
|
|
|
ах4 + bх2 + с =0 |
|
|
б) |
У рівнянні виду: |
|
|
|
(х + a)(х + b)(х + с)(х+ d) = m |
|
|
|
Якщо a+d= b+с, то помножити парами (х + a)(х + d) і (х + b)(х + с) |
|
|
|
Заміна: х2 + (а + d)x=t, |
|
|
|
тоді |
|
|
|
(х + a)(х + b)(х + с)(х + d)= т |
|
|
2. |
Шляхом рівносильних перетворень: дробово-раціональні рівняння: |
|
|
|
рівняння вигляду |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доведення нерівностей |
|
1.Довести нерівність: |
|
Доведення. Знайдемо різницю лівої та правої частин нерівності:
Сума додатних взаємно обернених чисел не менша за 2. |
|
Зауваження:рівність має місце при а = b. |
|
2.Довести нерівність: |
|
Доведення. Знайдемо різницю лівої та правої частин нерівності:
|
|
Зауваження:рівність має місце лише при а = bабо а = b = 0. |
|
Приклад. Доведемо нерівність |
|
Доведення. Подамо вираз |
|
Основні властивості числових нерівностей |
|
1.Якщо a > b, то b< a. |
|
Доведення |
|
a >b |
|
2.Якщо a<b, b<c, то a<c. |
|
Доведення |
|
a<b
(a–b)+(b–c) = a–b+ b–c= a–c<0 |
|
3.Якщо а<b, ас — будь-яке число, то а + с<b + с. |
|
Доведення |
|
a<b |
|
4.Якщо a<b, c>0, то aс <bс і
Якщо а<b, с<0, то ас>bc; |
|
Доведення |
|
a<b Отже, якщо а<bі с>0, то ас<bc; c<0, то ас>bс.
Нерівності |
|
Наслідки з властивостей числових нерівностей |
|
1.Якщо а<b + с, то а–с<b. |
|
Доведення
a<b + c |
|
2.Якщо а>0іb>0,іa<b,то |
|
Доведення
a<b
|
|
Приклад. Відомо, що а<b. Порівняємо значення виразів: 2а + 3і 2b+5. |
|
Розв'язання а<b | ∙2;оскільки 2>0, то 2а<2b|+3; 2а + 3<2b+3. 3<5|+2b; оскільки 2>0, то 2b + 3 < 2b+5.
Отже, |
|
Якщо точне значення величини х не відоме, але можна визначити, між якими числами а і Ь це значення міститься на числовій прямій (тобто a< х < Ь ), то кажуть, що значення величини оцінено х. |
|
Приклад. Відомо, що -1 <х <3. Оцінимо значення виразу 2x–5. |
|
Розв'язання |
|
Встановимо послідовність дій у виразі 2х–5: спочатку х помножимо на 2, а потім додамо до цього виразу -5: х |
|
Помножимо всі частини одержаної нерівності -1 <х <3 на 2 > 0, при цьому знак нерівності не зміниться: -2 <2х < 6. |
|
Додамо до всіх частин нерівності число -5, при цьому знак нерівності не зміниться: -7<2х–5<1. |
|
Теорема (властивість) про почленне додавання числових нерівностей |
||||||
|
Якщо а<bі c<d, то a + c<b+d. |
||||||
|
Доведення
|
||||||
|
Теорема (властивість) про почленне множення числових нерівностей |
||||||
|
Якщо 0<а<b і 0<c<d, то ac<bd. Доведення
Наслідок. Якщо 0<а<b, то an<bn, де п — натуральне число. |
||||||
|
Доведення |
||||||
|
|
(за теоремою про почленне множення числових нерівностей). |
|||||
|
Приклад 1. Відомо, що 3<а<4; 2 <b< 3. Оцінимо значення виразу:
1)а + b;2) а-b;3) аb;4) Розв'язання |
||||||
|
1) |
|
2)а- b = а+(-b) 2<b <3| ∙ (-1) - 2>-b>-3
|
3) |
|
4) (0<)2<b <3
|
|
|
Приклад 2. Доведемо нерівність (т + п)(тп + 1)>4тп, якщо т>0, п>0. |
||||||
|
Доведення
Використавши нерівність |
||||||
|
т + п ≥ 2
тп+1 ≥ 2 |
||||||
|
За теоремою про почленне множення нерівностей перемножимо нерівності (1) і (2) почленно. Тоді маємо:
(т + п)(тп + 1) ≥ 2 |
||||||
|
(т + п)(тп + 1) ≥ 4 (т + п)(тп + 1) ≥ 4тп, де m≥ 0, п ≥ 0. |
||||||
|
Нерівності з однією змінною та їхні системи і сукупності |
|
1.Нерівність з однією змінною Якщо двавиразизі змінноюпоєднатиодниміззнаків > (більше); < (менше); ≥ (більше або дорівнює); ≤ (менше або дорівнює), то отримаємо нерівність з однією змінною. |
|
Наприклад: х2 + 1>х–1;3х–1 ≥ x + 2;
Розв'язком нерівності зі змінною називається значення змінної, при якому дана нерівність перетворюється на правильну числову нерівність. Наприклад, для нерівності |
|
2.Система нерівностей з однією змінною Якщо треба знайти спільні розв'язки нерівностей з однією змінною, то кажуть, що треба розв'язати систему нерівностей. Систему нерівностей записують за допомогою фігурної дужки. |
|
Наприклад: |
|
Розв'язком системи нерівностей з однією змінною є значення змінної, яке є розв'язком кожної з нерівностей системи. |
|
Наприклад:х = 3є розв'язком системи 3 –3<1 і 2 ∙ 3 –1>3 є правильними нерівностями (х = 3є розв'язком кожної з нерівностей). |
|
3.Сукупність нерівностей з однією змінною Якщо ставиться завдання знайти значення змінної, яке є розв'язком хоча б однієї з даних нерівностей, то кажуть, що слід розв'язати сукупність нерівностей. Сукупність нерівностей записують за допомогою квадратної дужки. |
|
Наприклад: Розв'язком сукупності нерівностей з однією змінною називається таке значення змінної, яке є розв'язком хоча б однієї з нерівностей сукупності. |
|
Наприклад: х = 1є розв'язком сукупності є розв'язком нерівності 2х–1<3 (при х = 1ця нерівність перетворюється на правильну: 2 ∙ 1 –1< 3). |
|
Розв'язати нерівність (систему нерівностей або сукупність нерівностей) означає знайти всі її розв'язки або довести, що їх немає. |
|
|
Числовий проміжок — вид запису множин, що є розв'язками нерівностей з однією змінною. Види числових проміжків |
|
|
|
|
Проміжок |
Приклад |
|
|
|
1. а<х< b
|
2<x <3
|
|
|
|
2. а ≤ х ≤ b
|
2 ≤ х ≤ 3
|
|
|
|
3. х>а
|
х> -2
|
|
|
|
4. х ≥ а
|
х ≥ -2
|
|
|
|
5. х<а
|
х<3
|
|
|
|
6. х ≤ а
|
х ≤ 3
|
|
|
|
Переріз і об'єднання проміжків
Приклад 1. Розв'яжемосистему нерівностей
|
|
|
|
Розв'язання.(3;5)—спільна частина проміжків(3; + ∞) і (-∞; 5), тому (3;5) — це переріз проміжків (3; + ∞) і (-∞; 5)(розв'язок системи
Відповідь: (3; + ∞) |
|||
|
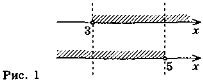
Приклад 2. Розв'яжемо систему нерівностей |
|||
|
|
|||
|
Розв'язання. Проміжок (-1;3) складається з чисел, які є розв'язком хоча б однієї з нерівностей 2 <х <3 або -1 <х <2,5, тому є об'єднанням цих проміжків (розв'язком сукупності).
Відповідь: (2; 3) |
|||
|
Дві нерівності називають рівносильними, якщо вони мають ті самі розв'язки. |
|
|
Деякі рівносильні перетворення нерівностей |
|
|
1.Якщо з однієї частини нерівності перенести в іншу частину доданки з протилежними знаками, то утвориться нерівність, рівносильна даній. Наприклад: 2x –3>6 і 2х>9 —рівносильні нерівності. |
|
|
2.Якщо обидві частини нерівності помножити (або поділити) на те саме додатне число, то утвориться нерівність, рівносильна даній.
Наприклад: 2x>6 і х>3, |
|
|
3.Якщо обидві частини нерівності помножити (поділити) на те саме від'ємне число і змінити знак нерівності на протилежний, то утвориться нерівність, рівносильна даній. |
|
|
Наприклад: -3х>6 і х<-2; |
|
|
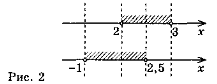
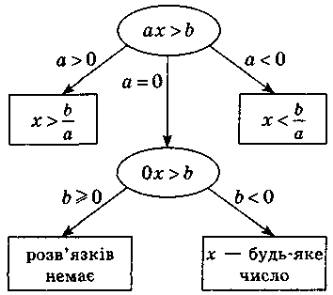
Лінійна нерівність з однією змінною— нерівність виду ах>b, або ах<b, або ах ≥ b, або ах ≤ b, де а,b— дані числа, ах — змінна. Наприклад: 3х>1; -x<-3; 0х>3; 0х<0 —лінійні нерівності. |
|
|
Схема розв'язування лінійної нерівності |
|
|
|
|
|
Приклад розв'язування нерівності, що зводиться до лінійної: |
|
|
Розв'язати нерівність 9(х–1)+5х<17х–11 |
Коментар |
|
9х–9+5х<17х–11 14х–9<17х–11 |
1. Виконаємо тотожні перетворення лівої(і правої) частин нерівності. |
|
14х–17х<-11 + 9 -3х< -2 |
2.Перенесемо відомі доданки в однучастину нерівності, а невідомі — в іншу. Тотожно перетворимо обидві частини. |
|
х >
x
Відповідь: |
3. Оскільки коефіцієнт при х у лівій частині утвореної нерівності не дорівнює нулю, поділимо на нього обидві частини нерівності, змінивши її знак на протилежний (бо -3<0). Запишемо відповідний числовий проміжок — це і є відповідь — розв'язок даної нерівності. |
|
Основні кроки розв'язування нерівностей з однією змінною |
|
|
1.Якщо нерівність містить дроби, то множимо обидві частини нерівності на найменший спільний знаменник усіх дробів, які входять у нерівність. |
|
|
2.Якщо в нерівності є дужки, то розкриваємо їх. |
|
|
3.Переносимо доданки зі змінною в одну частину нерівності, а інші доданки — у другу частину. |
|
|
4.Зводимо подібні доданки,одержуємо лінійну нерівність. Розв'язуємо лінійну нерівність за схемою (див.опорний конспект № 8). |
|
|
Приклад. Розв'яжемо нерівність: |
|
|
3(у + 1)+2у– 1 <6у; 3у + 3 + 2у–1<6у; |
5y+2<6y; 5у–6у<-2; -у<-2; у>2. |
|
Відповідь: y |
|
|
Основні кроки розв'язування системи нерівностей з однією змінною |
|
1. Розв'язуємо кожну нерівність системи. 2. Зображуємо множину розв'язків кожної нерівності на однійкоординатній прямій. 3. Знаходимо переріз числових проміжків, записуємо відповідь. |
|
Приклад. Розв'яжемо систему нерівностей Розв'язання
|
|
Основні кроки розв'язування сукупності нерівностей з однією змінною 1. Розв'язуємо кожну нерівність сукупності. 2. Зображуємо множину розв'язків кожної нерівності на однійкоординатній прямій. 3. Знаходимо об'єднання числових проміжків, записуємо відповідь. |
|
Приклад. Знайдемо розв'язок сукупності нерівностей |
|
Розв'язання
|
|
Відповідь: x |
|
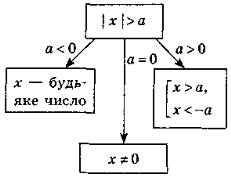
Найпростіші нерівності з модулем |
|
|
|
|
|
Наприклад: |x –1|<3;
x |
Наприклад: |x – 1|> 3;
x |
|
Приклад 1. Визначимо, при яких значеннях змінної має зміст вираз
Розв'язання |
|
|
Вираз |
|
|
|
|
|
Відповідь: [-1,5; 4,5). |
|
|
Приклад 2. Розв'яжемо нерівність | 7х + 8 |<2. |
|
|
Розв'язання |
|
|
Дана нерівність рівносильна системі: |
|
|
Відповідь: |
|
|
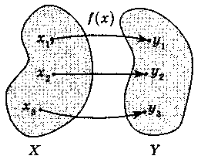
Функція — це залежність змінної у від змінної х, при якій кожному значенню х відповідає єдине значення у. |
|||||
|
|
Позначається: y = f(x), де х — аргумент (незалежна змінна); у — функція, значення функції (залежна змінна);f(x0) — значення функції в точці х0. |
||||
|
Приклад. Дано функцію f(x) = x2-3х + 2. Знайдемо: 1) f(0)2) f(-1);3) f(а). Розв’язання |
|||||
|
1)f (0) = 02–3 ∙ 0 + 2 = 2; 2)f (-1) = (-1)2–3 ∙ (-1)+2 = 6; 3)f(a) = a2– 3a + 2. |
|||||
|
|
Область визначення функції D(f)— це множина всіх значень, яких набуває аргумент. |
|
|||
|
|
Як знайти область визначення функціїy = f(x) |
|
|||
|
|
1.Якщо f(x) — многочлен, то D(f) = R. |
|
|||
|
2.Якщо |
|||||
|
3.Якщо |
|||||
|
Приклад.Знайдемо область визначення функції: |
|||||
|
|
Розв'язання |
|
|||
|
|
1) 3х2–х+ 1— многочлен, тому D(y) = R;
2)
3)
Отже, D(y)= (-∞; 0) |
|
|||
|
|
Область значень функції E(f)— множина всіх значень змінної у, яких вона може набувати при всіх значеннях аргументу, взятих з D(f). |
|
|||
|
|
Приклад. Знайдемо область значень функції у = Розв'язання |
|
|||
|
|
При всіх x |
|
|||
|
|
Числовою функцієюназивають функцію, область визначення й область значень якої є числовими множинами. |
|
|||
|
|
Графіком функціїy = f(x)називають множину всіх точок координатної площини з координатами (х; f(x)), де х «пробігає» всю область визначення f(x) (ay — відповідне значення функції / у точці х). |
|
|||
|
|
Деякі елементарні функції та їхні графіки |
|
|||
|
|
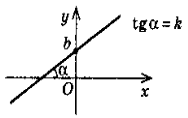
1. y = kx + b—лінійна функція
|
2. у = x2
|
|
||
|
|
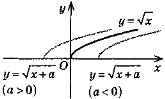
3.у =
|
4.y =
|
|
||
|
|
|
|
|
||
|
|
Найпростіші перетворення графіків функцій |
|
|||
|
|
№ з/п |
Формула залежності |
Приклад |
Перетворення |
|
|
|
1 |
y = -f(х) |
|
Симетрія відносно осі Ох |
|
|
|
2 |
y = f(х)+ a |
|
Паралельне перенесення вздовж осі Оу на а одиниць (якщо а> 0, то вгору, якщо а< 0, то вниз) |
|
|
|
3 |
y = f(х + a) |
|
Паралельне перенесення вздовж осі Ох на +а одиниць (якщо а> 0— вліво, якщо а< 0 — вправо) |
|
|
|
4 |
y = kf(х)(k >0) |
|
Той самий вигляд, що і y = f(x), тільки розтяг-нуто, якщо k> 1, і стиснуто, якщо 0<k<1 |
|
|
|
|
|
|
|
|
|
Функція виду у = ax2+ bx + c, де а |
|||
|
Наприклад: |
|||
|
Графік квадратичної функції — парабола, вітки якої напрямлені вгору, якщо а > 0, і вниз — якщо а < 0 . |
|||
|
Координати вершини (х0;у0)параболи графіка у = ах2 + bх + с обчислюються за формулами: |
|||
|
|
|||
|
Наприклад: у функціїу = х2+2х–3, яка є квадратичною, графік — парабола. Вітки параболи напрямлені вгору (а = 1 > 0), а координати вершини: |
|||
|
|
|||
|
або y0 = f (-1) = (-1)2+2 ∙ (-1)–3= 1–2–3= -5 + 1 = -4. |
|||
|
Тобто вершина параболи (-1; - 4). |
|||
|
|
Побудова графіка функції у = ах2 + bх + с, а |
|
|
|
|
Спосіб1 |
Спосіб2 |
|
|
|
1.Обчислити абсцису вершини |
1.Виділити повний квадрат:
ах2 +bх + с = а |
|
|
|
2.Підставити х0у рівнянняі знайти у0. 3. Побудувати параболу у = ах2з вершиною в точці (х0;у0).Якщо а >0, вітки параболи напрямлені вгору, якщоа <0— вниз. 4. Для більшої точності побудови знайти точки перетинуграфіка з координатнимиосями. |
= а 2.Використавши схему геометричних перетворень графіківфункцій, виконати побудовупараболи у= х2, потім її розтягнення (або стиснення) до параболи у= ах2, а потім виконатипаралельне перенесення у= ах2вздовж осі Ох на –ті вздовжосі Оуна п. |
|
|
|
|
|
|
|
|
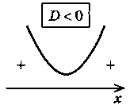
Нерівності виду ах2+ bх + с>0 (<0; ≥ 0;≤ 0) називаються квадратними, якщо а |
|
||
|
|
Приклад.3х2–2х–1>0,x2–9 ≥ 0,х2–2х<0,-х2>0— квадратні нерівності (з різними значеннями коефіцієнтів квадратного тричлена в лівій частині). |
|
||
|
|
Схема розв'язування квадратних нерівностей |
|
||
|
|
1.Знайти дискримінант D, а потім корені x1,x2квадратного тричлена (якщо вони існують). |
|
||
|
|
2.Побудуватиескізграфікаквадратичноїфункції у= ах2+ bх + с (з урахуванням знака коефіцієнта а та знайденого знака дискримінанта Dі коренів). |
|
||
|
|
3.Для випадку >0 відповідно отримаємо проміжок, для якого точки параболи лежать вище осі Ох, для випадку < 0 відповідно отримаємо проміжки, для яких точки параболи лежать нижче осі Ох. |
|
||
|
|
Схема розв'язування нерівності ах2+ bx + c>0залежно від а і D |
|
||
|
|
ax2+bx + c>0(D = b2– 4ac)
|
|
||
|
|
x |
x |
x |
|
|
|
|
|
||
|
Рівняння з двома змінними Приклади: х2 + у2= 25, ху = 4, х + ху = 1. |
|||||||||
|
Супутні поняття |
|||||||||
|
1.Розв'язок рівняння з двома змінними х і у — це впорядкована пара (х;у), яка перетворює рівняння на правильну рівність. |
|||||||||
|
Наприклад, пара (2;3) є розв'язком рівняння ху = 6, бо при х = 2іy = 3 дане рівняння має вигляд 2 ∙ 3 = 6, тобто утворюється правильна рівність. |
|||||||||
|
2.Степінь цілого рівняння з двома змінними р(х;у) = 0визначається як степінь многочлена Р(х;у), якщо він зведений до стандартного вигляду. Наприклад, х2+ ху + у = 0— рівняння другого степеня. |
|||||||||
|
Графік рівняння з двома змінними х і у — це множина точок координатної площини з координатами (х; у), де пара (х; у) є розв'язком даного рівняння з двома змінними. |
|||||||||
|
Як побудувати графік рівняння з двома змінними 1.Якщо рівняння можна звести до вигляду (х–a)2 +(y–b)2 =R2,де а, b— довільні числа, aR>0, то графіком цього рівняння буде коло з центром (а;b)і радіусом R. |
|||||||||
|
2.В інших випадках (якщо немає модуля) виражаємо у через х і будуємо графік утвореної функції y = f(x). |
|||||||||
|
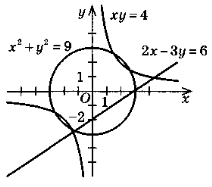
Приклад.Побудуємо графік рівняння:1)2x–3у = 6;2) х2 + у2=9;3) ху= 4. |
|||||||||
|
Розв'язання (див. рисунок)
|
|||||||||
|
1)2х–3у = 6 |
|||||||||
|
|
х |
0 |
3 |
|
|
||||
|
|
y |
-2 |
0 |
|
|||||
|
2)х2 + у2= 9 = 32 —рівняння колаз центром (0;0) і радіусом 3.
3)ху = 4;у = |
|||||||||
|
|
х |
-4 |
-2 |
-1 |
1 |
2 |
4 |
|
|
|
|
у |
-1 |
-2 |
-4 |
4 |
2 |
1 |
|
|
|
|
|||||||||
|
Системи рівнянь з двома змінними |
|
Якщоставитьсязавданнязнайтивсіспільнірозв'язки двох (і більше) рівнянь з двома змінними, то кажуть, що треба розв'язати систему рівнянь з двома змінними. |
|
Розв'язком системи рівнянь з двома змінними х і у називається така пара значень змінних (х;у), яка є розв'язком кожного з рівнянь системи. |
|
Наприклад,пара(2;3)єрозв'язкомсистемирівнянь |
|
Розв'язати систему рівнянь з двома змінними означає знайти всі її розв'язки, або довести, що їх немає. ! Якщо система не має розв'язків, її називають несумісною. |
|
Як розв'язати систему рівнянь з двома змінними хі у графічним способом |
|
1.Будуємо графіки кожного з рівнянь системи втій самійпрямокутній системі координат. 2. Знаходимо всі точки перетину побудованих графіків і визначаємо їхні координати. Ці координати є розв'язками даноїсистеми рівнянь. |
|
Розв'язування систем рівнянь з двома змінними способом підстановки |
|
Якщо в системі рівнянь з двома змінними одне з рівнянь є рівнянням першого степеня (лінійним), то таку систему можна розв'язати способом підстановки.
Приклад.Розв'яжемо систему рівнянь Розв'язання |
|
1.3х–у= 2— рівняння першого степеня, виразимо у через х із цього рівняння: у = 3х–2. |
|
2.Підставимозамістьуудругерівняннявираз3х–2і розв'яжемо одержане рівняння зі змінною х: 3x2+(3x–2)2=28; 3х2 + 9x2–12х + 4–28 = 0;12x2–12х–24 = 0; х2–х–2= 0; х1=-1; х2 =2. |
|
3.За формулою у = 3х–2знайдемо відповідні значення змінної у: у1=3х1–2= 3 ∙ (-1)–2= -5; у2=3х2–2= 3 ∙ 2–2= 4.Отже, система має розв'язки: х1 = -1; у1=-5;х2 = 2;у2 = 4. Відповідь: (-1;-5);(2; 4). |
|
(Закінчення опорного конспекту № 20 див. у наступному уроці.) |
|
Як розв'язати задачу, склавши систему рівнянь з двома змінними |
|
1. Виділяємо в умові задачі дві невідомі величини (шукані або ті, через які можна виразити шукані величини) і позначаємо їх буквами х і у. |
|
2. За умовою задачі складаємо два рівняння зі змінними х і y. |
|
3.Розв'язуємо систему цих рівнянь. |
|
4. Розтлумачуємо знайдені розв'язки відповідно до умови задачі. Записуємо відповідь. |
|
Відсотком (процентом) називається сота частина цілого (яке приймається за одиницю).
1 % від числа а дорівнює Основні задачі на відсотки |
|
1.Знаходження відсотка від числа. р%від числа а дорівнює
Приклад.7% від числа 300 дорівнює |
|
2.Знаходження числа за заданою величиною його відсотка. Якщо р%якого-небудь числа становить b, то все число дорівнює
Приклад.Число, 30% якого дорівнює 24,— це число х = 24:
= |
|
3.Знаходження відсоткового відношення двох чисел.
Число а від числа bстановить Приклад. Число 26 від числа 65 становить
Банківські відсотки— відсоткові гроші по банківських вкладах, що нараховуються: |
|
а)щомісяця (протягом року).
|
|
б)щорічно (під певний відсоток річних).
|
|
Випадкова подія— подія, яка може або відбутися, або не відбутися (за певних обставин) при багаторазовому випробуванні. |
|
Приклади: а) назавтра піде дощ; б) виграш у лотерею 10 грн. Якщо подія обов'язково відбудеться при багаторазовому випробуванні, то вона називається вірогідною. |
|
Приклади: а) після четверга наступає п'ятниця; б) сонце сходить на сході. |
|
Якщо подія не відбудеться при багаторазовому випробуванні, то вона називається неможливою. |
|
Приклад:а) після зими настає літо; б) з ящика, у якому є тільки білі кульки, витягують чорну кульку. |
|
Ймовірність(випадкової події) — це число, яке показує відношення числа випробувань, у яких дана подія відбулась, до числа всіх випробувань. |
|
Р(А)= |
|
Властивості ймовірності будь-якої події |
|
1. 0 ≤ Р(А) ≤ 1. 2. Якщо А — вірогідна подія, то Р(А) = 1. 3. Якщо А — неможлива подія, то Р(А) = 0. 4. Якщо А — випадкова подія, то 0<Р(А)<1. |
|
Математична статистика — розділ математики, який присвячений методам збору й обробки математичних даних та їх використанню для наукових і практичних спостережень. |
||||||||
|
Основні поняття математичної статистики |
||||||||
|
1. Статистичні дані — сукупність чисел, які дають кількіснухарактеристику ознак певних об'єктів та явищ, що насцікавлять. 2. Відібрану для спостереження сукупність об'єктів називаютьвибірковою сукупністю або вибіркою. 3. Кількість об'єктівсукупності називають об'ємом сукупності. 4. Числа, що є значеннями ознак кожної групи, на які можнаподілити вибірку, називають варіантами; послідовність варіант називають варіаційним рядом. 5. Частоти— числа, які показують, скільки разів повторювалось кожне значення ознаки сукупності. 6. Відношення частоти до об'єму вибірки називають відносноючастотою. |
||||||||
|
Приклад.Нехай дано вибірку: 2; 2; 2; 3; 3; 3; 3; 3; 4; 4; 4; 4; 4; 4; 5; 5; 5; 5; 5; 6. х1=2; х2=3; х3=4; х5 =5; х6= 6 — варіанти вибірки; 2; 3; 4; 5; 6 — варіаційний ряд. |
||||||||
|
Частота варіанти х1дорівнює 3; варіанти х2— 5; варіанти х3— 6; варіанти х4 — 5; варіанти х5— 1. Відносна частотаваріанти х1 дорівнює |
||||||||
|
Для обробки статистичних даних виконують їх зведення, тобто упорядковують, узагальнюють статистичні дані. |
||||||||
|
Способи зведення статистичних даних: 1) складання статистичного ряду; 2) складання статистичної таблиці розподілу вибірки; 3) складання полігона частот; 4) складання гістограм. |
||||||||
|
Приклад.Економіст, аналізуючи тарифні розряди працівників одного із цехів заводу, вибрав документи 20 робітників і виписав з них послідовність чисел, що вказують на тарифні розряди: 4; 4; 3; 2; 5; 2; 3; 5; 4; 3; 3; 2; 5; 4; 5; 4; 6; 3; 4; 5 — вибірка, що піддається обробці. |
||||||||
|
Статистичний ряд цієї вибірки: 2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 6; Статистична таблиця розподілу вибірки: |
||||||||
|
|
Тарифний розряд х1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
|
Кількість робітників п |
3 |
5 |
6 |
5 |
1 |
|
|
|
|
||||||||
|
|
|
|||||||
|
Вибірки характеризуються центральними тенденціями:середнім значенням, модою і медіаною |
|
Середнє арифметичне значення
|
|
Зважене середнє арифметичне значення
|
|
Мода вибірки— це значення ознаки, яка найбільш часто повторюється у вибірці. |
|
Медіаною вибірки називається варіанта, яка розміщена посередині варіаційного ряду. |
|
Приклад.Дано вибірку вимірювання повітря температури (t, °С) у першу декаду квітня: 5; 6; 4; 3; 4; 5; 6; 2; 4; 6. Складіть статистичний ряд; визначте варіанти та їхні частоти; складіть варіаційний ряд, для якого знайдіть середнє зважене значення, моду та медіану. |
|
Розв'язання Статистичний ряд даної вибірки: 2, 3, 4, 4, 4, 5, 5, 6, 6, 6. Варіанти, варіаційний ряд: 2, 3, 4, 5, 6; частоти відповідно дорівнюють 1, 1, 3, 2, 3. |
|
Середнє зважене значення:
|
|
Мода дорівнює 4 і 6, бо 4 і 6 повторюються найчастіше — по 3 рази. |
|
Оскільки у варіаційному ряді 5 чисел: 2, 3, 4, 5, 6, то медіана дорівнює 4. |
|
|
Арифметична прогресія — числова послідовність, у якій кожний наступний член, починаючи з другого, дорівнює попередньому члену, до якого додається те саме число.Це число називають різницею арифметичної прогресії. |
|
|
|
Приклад. 1; 3; 5; 7; 9 — арифметична прогресія. 3 – 1= 5 – 3 = 7 – 5= 9 – 7= 2; 2 — різниця арифметичної прогресії. |
|
|
|
Рекурентна формула арифметичної прогресії |
|
|
|
ап+1=ап+d, d— різниця арифметичної прогресії. d = aп+1– ап. |
|
|
|
|
|
|
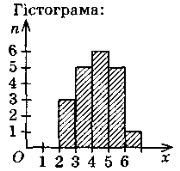
Властивості арифметичної прогресії |
||
|
1. ап— п-йчлен арифметичної прогресії, є середнім арифметичним двох сусідніх за ним членів. |
||
|
2.Якщо (ап) — арифметична прогресія (скінченна), то: |
||
|
|
||
|
Сума двох членів скінченної арифметичної прогресії, які рівновіддалені від її кінців дорівнює сумі крайніх членів цієї прогресії. |
||
|
3.Теорема*. Будь-яка арифметична прогресія(ап) може бути задана формулоюan=kn + b, де kі b— деякі числа; і навпаки, якщо послідовність (ап) задана формулою an=kn + b, де kі b— деякі числа, то ця послідовність є арифметичною прогресією. |
||
|
Сума перших п членів арифметичної прогресії |
|
1.Якщо a1 і an — перший і п-й члени арифметичної прогресії (аn), то сума Snперших п членів цієї прогресії дорівнює:
|
|
2.Якщо a1і d— перший член і різниця арифметичної прогресії (ап), то сума Snперших п її членів дорівнює:
|
|
Приклад.Знайдемо суму перших десяти членів арифметичної прогресії (аn), у якої: 1)a1 =10, а2=-10;2)а1 =2, d = -3. Розв'язання |
|
1)S10= |
|
2)S10 = = -23 ∙ 5 = -115. Відповідь: 1) 0; 2)-115. |
|
Геометричною прогресією називається послідовність відмінних від нуля чисел, кожний член якої, починаючи з другого, дорівнює попередньому, помноженому на те саме число (знаменник геометричної прогресії). |
|
Приклад. 3; 9; 27; 81; 243; ... — геометрична прогресія, бо а2=а1∙ 3; а3=а2 ∙ 3; а4=а3∙ 3; ... . (3 — знаменник цієї прогресії). |
|
Рекурентна формула геометричної прогресії |
|
Якщо (bп)— геометрична прогресія, то bn+1 = bnq, де bп— п-йчлен; q— знаменник геометричної прогресії.
З рекурентної формули випливає: |
|
Властивості геометричної прогресії: |
|
а) для кожного члена геометричної прогресії, починаючи з другого: |
|
б) якщо (bп)— скінченна геометрична прогресія, то b1∙ bn= b2 ∙ bn-1 = b3 ∙ bn-2= const(b1і bn— крайні члени цієї прогресії). |
|
Формули суми перших п членів геометричної прогресії |
|
Якщо(bп)— геометрична прогресія,q— її знаменник, aSn— сума перших п її членів, то:
або ! Зауваження: якщо q = 1, тоSn= b1 ∙n(b1 =b2=... = bn). |
|
Приклад 1. Знайдемо суму перших восьми членів геометричної прогресії (bn):3; -6; 12; ... . Розв'язання
Маємо b1 =3, q =
S8 = Відповідь: -255. |
|
Приклад 2. Знайдемо перший член геометричної прогресії (bп), якщо її четвертий член утричі більший за третій, а сума перших п'яти членів дорівнює -12,1. Розв'язання
Оскількиb4= 3b3,тоq = 3.ЗаумовоюS5=-12,l,тому,оскільки Відповідь: -0,1. |
|
Нескінченна геометрична прогресія, у якої | q| < 1 |
|
Приклади:
а)1;
б)3;
в)100; 10; 1;
г)32; 0,32; 0,0032; ...q= |
|
Якщо(bn)— нескінченна геометрична прогресія, у якої | q| < 1, то сума всіх її членів Sобчислюється за формулою
|
|
Приклад 1. Знайдемо суму нескінченної геометричної прогресії (bn): 6; -2; ... . Розв'язання
За умовою b1= 6; b2 = -2, отже, q=
Відповідь; 4,5. |
|
Приклад 2. Запишемо число 0,(7) у вигляді звичайного дробу. Розв'язання Запис 0,(7) означає нескінченний періодичний дріб 0,7777....
Його можна подати як нескінченну суму Доданки цієї суми є членами нескінченної геометричної прогресії, у якої
b1=
Відповідь: |


про публікацію авторської розробки
Додати розробку

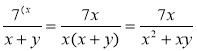 .
.
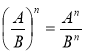
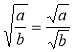 і навпаки,
і навпаки,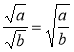 ;
;
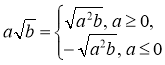
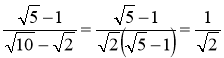 ;
;
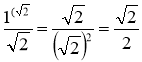 ;
; 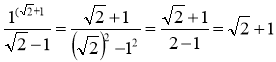 .
.
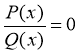 , де P(х) і Q(х) — многочлени від однієї змінної, рівносильні системі:
, де P(х) і Q(х) — многочлени від однієї змінної, рівносильні системі:
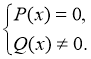
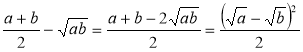 . Оскільки
. Оскільки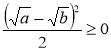 ,тобтонерівність
,тобтонерівність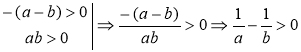 .
.
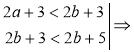 2а + 3<2b + 5.
2а + 3<2b + 5.
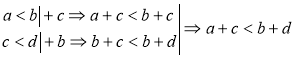 .
.
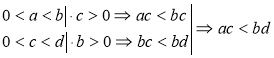 .
.
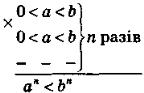
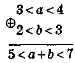
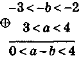
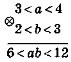
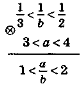

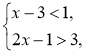 бо прих = 3
бо прих = 3
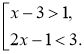
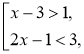 бо х = 1
бо х = 1
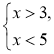 (рис. 1).
(рис. 1).
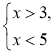 ).
).
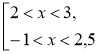 (рис. 2).
(рис. 2).
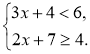
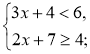
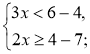
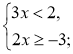
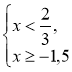 (див. рисунок).
(див. рисунок).  Відповідь: х
Відповідь: х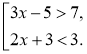
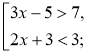
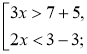
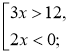
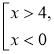 (див. рисунок).
(див. рисунок).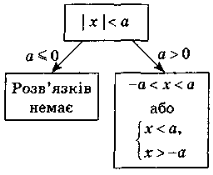
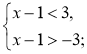
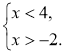
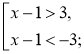
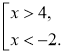
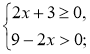
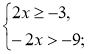
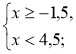 х є [-1,5; 4,5).
х є [-1,5; 4,5).
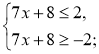
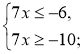
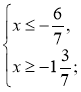
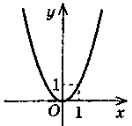
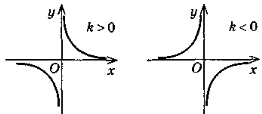
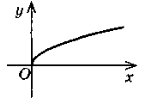
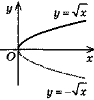
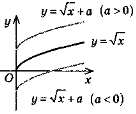
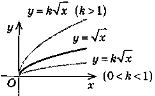
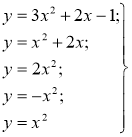 — квадратичні функції.
— квадратичні функції.
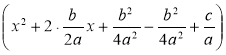 =
=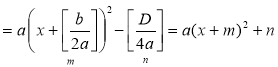 .
.
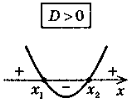
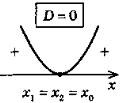
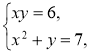 бо х = 2і у= 3 є розв'язком кожного, з рівнянь системи.
бо х = 2і у= 3 є розв'язком кожного, з рівнянь системи.
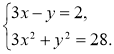
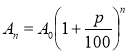 — формула складних відсотків, де A
— формула складних відсотків, де A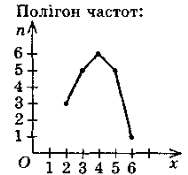
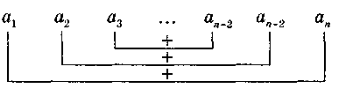
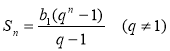 (2)
(2)
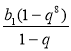 =
= 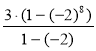 =
= 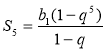 ,тобто
,тобто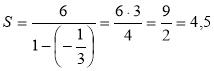 .
.
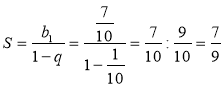 . Тому 0,(7)=
. Тому 0,(7)=