Формування базових компетентностей на уроках математики

Про матеріал

Методичний посібник «Формування базових компетентностей на уроках математики» містить вимоги оновленої навчальної програми з математики для учнів 5-9 класів (2017 рік) та навчальної програми з математики для учнів 10-11 класів загальноосвітніх навчальних закладів щодо формування десяти компетентностей.

Перегляд файлу

Гімназія с. Мишлятичі

Формування

базових компетентностей на уроках математики

2022

Укладач: Падяк Марія Йосифівна – вчитель математики, спеціаліст вищої категорії, відмінник освіти.

Рецензенти: спеціаліст вищої категорії, старший учитель гімназії с. Мишлятичі Строган Л.І., спеціаліст вищої категорії, старший учитель Гусаківського ЗЗСО I-III ступенів Кушнір О.Є.

Дано коротку характеристику чотирьох наскрізних ліній; поради вчителю, щодо формування компетентностей на уроках математики.

У посібнику зібрані прикладні задачі, задачі історичного та краєзнавчого змісту, задачі з природничим сюжетом, інформаційні задачі.

Є фрагменти уроків та позакласних заходів.

Рекомендовано на допомогу педагогам.

ЗміСТ

ЗМІСТ

ВСТУП

РОЗДІЛ 1. КОМПЕТЕНТІСНИЙ ПІДХІД ПРИ ВИВЧЕННІ МАТЕМАТИКИ

РОЗДІЛ 2. ЗАДАЧІ ДЛЯ ФОРМУВАННЯ КЛЮЧОВИХ КОМПЕТЕНТНОСТЕЙ

РОЗДІЛ 3. ФРАГМЕНТИ РОЗРОБОК УРОКІВ ТА ПОЗАКЛАСНИХ ЗАХОДІВ

ВИСНОВКИ

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

ВСТУП

Освіта, яка не вчить успішно жити в суспільстві, не має жодної цінності

Випускник основної школи — це патріот України, який знає її історію; носій української культури, який поважає культуру інших народів; компетентний мовець, що вільно спілкується державною мовою, володіє також рідною (у разі відмінності) й однією чи кількома іноземними мовами, має бажання і здатність до самоосвіти, виявляє активність і відповідальність у громадському й особистому житті, здатний до підприємливості та ініціативності, має уявлення про світобудову, бережно ставиться до природи, безпечно й доцільно використовує досягнення науки і техніки, дотримується здорового способу життя.

Провідним засобом реалізації вказаної мети є запровадження компетентнісного підходу у навчально-виховний процес загальноосвітньої школи шляхом формування предметних і ключових компетентностей.

Компетентісний підхід до освіти – це спроба звести у відповідність освіти і потреби ринку праці. Він не є чимось новим, штучно створеним, а гармонійно поєднує традиційний підхід викладання, головним завданням якого є формування сталих знань, вмінь та навичок і особистісно-орієнтовану форму навчання, метою якої є створення умов для розвитку та самореалізації кожного учня.

Оскільки компетентність – це не проста сума знань, умінь та навичок, а психосоціальна риса, яка надає учневі сили та впевненості у власній успішності, можливості ефективно взаємодіяти з навколишнім середовищем, то задля формування компетентностей в учнів виникає потреба змінювати підходи до викладання предметів, форми роботи, змісту освіти, оцінюванню результативності роботи педагога.

РОЗДІЛ 1. КОМПЕТЕНТІСНИЙ підхід при вивченні математики

Курс математики основної школи логічно продовжує реалізацію завдань математичної освіти учнів, розпочату в початкових класах, розширюючи і доповнюючи ці завдання відповідно до вікових і пізнавальних можливостей школярів. В основу побудови змісту та організації процесу навчання математики покладено компетентнісний підхід, відповідно до якого кінцевим результатом навчання предмета є сформовані певні компетентності, як здатності учня застосовувати свої знання в навчальних і реальних життєвих ситуаціях, повноцінно брати участь в житті суспільства, нести відповідальність за свої дії.

В основу побудови змісту та організації процесу навчання математики покладено компетентнісний підхід, відповідно до якого кінцевим результатом навчання предмета є сформовані певні компетентності, як здатності учня застосовувати свої знання в навчальних і реальних життєвих ситуаціях, повноцінно брати участь в житті суспільства, нести відповідальність за свої дії.

Нині людина живе і працює у світі, що постійно змінюється. Для того щоб учень став активним учасником створення нового і прогресивного в майбутньому, навчання і виховання мають спрямовуватися на формування творчої особистості, здатної до самовдосконалення.

Завдання вчителя не доносити істину, а вчити її знаходити. Дитину спочатку потрібно зацікавити, навчити хотіти й прагнути, а вже потім — знати й уміти. Процес навчання є своєрідним процесом самостійного «відкриття» учнем уже відомих у науці знань.

Під час навчання математики необхідно систематично розвивати та зміцнювати пізнавальний інтерес учнів. Важливим завданням вчителя формування в учнів стійких компетентностей на уроках математики та в позаурочний час. Це має вагоме освітнє та виховне значення.

Навчання математики має зробити певний внесок у формування ключових компетентностей.

Таблиця 1. Ключові компетентності

№	Ключові компетентності	Компоненти
1	Спілкування державною мовою	Уміння: ставити запитання і розпізнавати проблему; міркувати, робити висновки на основі інформації, поданої в різних формах (у таблицях, діаграмах, на графіках); розуміти, пояснювати і перетворювати тексти математичних задач (усно і письмово), грамотно висловлюватися рідною мовою; доречно та коректно вживати в мовленні математичну термінологію, чітко, лаконічно та зрозуміло формулювати думку, аргументувати, доводити правильність тверджень; поповнювати свій словниковий запас. Ставлення: розуміння важливості чітких та лаконічних формулювань. Навчальні ресурси: означення понять, формулювання властивостей, доведення теорем.
2	Спілкування іноземними мовами	Уміння: спілкуватися іноземною мовою з використанням числівників, математичних понять і найуживаніших термінів; ставити запитання, формулювати проблему; зіставляти математичний термін чи буквене позначення з його походженням з іноземної мови, правильно використовувати математичні терміни в повсякденному житті. Ставлення: усвідомлення важливості вивчення іноземних мов для розуміння математичних термінів та позначень, пошуку інформації в іншомовних джерелах. Навчальні ресурси: тексти іноземною мовою з використанням статистичних даних, математичних термінів.
3	Математична компетентність	Уміння: оперувати числовою інформацією, геометричними об’єктами на площині та в просторі; встановлювати відношення між реальними об’єктами навколишньої дійсності (природними, культурними, технічними тощо); розв’язувати задачі, зокрема практичного змісту; будувати і досліджувати найпростіші математичні моделі реальних об'єктів, процесів і явищ, інтерпретувати та оцінювати результати; прогнозувати в контексті навчальних та практичних задач; використовувати математичні методи у життєвих ситуаціях. Ставлення: усвідомлення значення математики для повноцінного життя в сучасному суспільстві, розвитку технологічного, економічного й оборонного потенціалу держави, успішного вивчення інших дисциплін. Навчальні ресурси: розв'язування математичних задач, зокрема таких, що моделюють реальні життєві ситуації.
4	Основні компетентності у природничих науках і технологіях	Уміння: розпізнавати проблеми, що виникають у довкіллі і які можна розв’язати засобами математики; будувати та досліджувати математичні моделі природних явищ і процесів. Ставлення: усвідомлення важливості математики як універсальної мови науки, техніки та технологій. Навчальні ресурси: складання графіків та діаграм, які ілюструють функціональні залежності результатів впливу людської діяльності на природу
5	Інформаційно- цифрова компетентність	Уміння: структурувати дані; діяти за алгоритмом та складати алгоритми; визначати достатність даних для розв’язання задачі; використовувати різні знакові системи; знаходити інформацію та оцінювати її достовірність; доводити істинність тверджень. Ставлення: критичне осмислення інформації та джерел її отримання; усвідомлення важливості ІКТ для ефективного розв’язування математичних задач. Навчальні ресурси: візуалізація даних, побудова графіків та діаграм за допомогою програмних засобів.
6	Уміння вчитися впродовж життя	Уміння: визначати мету навчальної діяльності, відбирати й застосовувати потрібні знання та способи діяльності для досягнення цієї мети; організовувати та планувати свою навчальну діяльність; моделювати власну освітню траєкторію, аналізувати, контролювати, коригувати та оцінювати результати своєї навчальної діяльності; доводити правильність власного судження або визнавати помилковість. Ставлення: усвідомлення власних освітніх потреб та цінності нових знань і вмінь; зацікавленість у пізнанні світу; розуміння важливості вчитися впродовж життя; прагнення до вдосконалення результатів своєї діяльності. Навчальні ресурси: моделювання власної освітньої траєкторії
7	Ініціативність і підприємливість у сфері культури	Уміння: генерувати нові ідеї, вирішувати життєві проблеми, аналізувати, прогнозувати, ухвалювати оптимальні рішення; використовувати критерії раціональності, практичності, ефективності та точності, з метою вибору найкращого рішення; аргументувати та захищати свою позицію, дискутувати; використовувати різні стратегії, шукаючи оптимальних способів розв’язання життєвого завдання. Ставлення: ініціативність, відповідальність, упевненість у собі; переконаність, що успіх команди – це й особистий успіх; позитивне оцінювання та підтримка конструктивних ідей перспективи, створення об’ємно-просторових композицій; унаочнювати математичні моделі, зображати фігури, графіки, рисунки, схеми, діаграми, усвідомлення взаємозв’язку математики та культури на прикладах з архітектури, живопису, музики та ін.; розуміння важливості внеску математиків у загальносвітову культуру. Навчальні ресурси: математичні моделі в різних видах мистецтва.
8	Екологічна грамотність і здорове життя	Уміння: аналізувати і критично оцінювати соціально-економічні події в державі на основі статистичних даних; враховувати правові, етичні, екологічні і соціальні наслідки рішень; розпізнавати, як інтерпретації результатів вирішення проблем можуть бути використані для маніпулювання. Ставлення: усвідомлення взаємозв’язку математики та екології на основі статистичних даних; ощадне та бережливе відношення до природніх ресурсів, чистоти довкілля та дотримання санітарних норм побуту; розгляд порівняльної характеристики щодо вибору здорового способу життя; власна думка та позиція до зловживань алкоголю, нікотину тощо. Навчальні ресурси: навчальні проекти, задачі соціально-економічного, екологічного змісту.

Оновлена програма для 5-9 класів 2017 року містить поняття наскрізних ліній.

Характеристика наскрізних ліній

Наскрізна лінія «Екологічна безпека й сталий розвиток» спрямована на формування в учнів соціальної активності, відповідальності та екологічної свідомості, готовності брати участь у вирішенні питань збереження довкілля і розвитку суспільства, усвідомлення важливості сталого розвитку для майбутніх поколінь.

Проблематика наскрізної лінії «Екологічна безпека та сталий розвиток» реалізується в курсі математики, насамперед, через завдання з реальними даними про використання природних ресурсів, їх збереження та примноження. Аналіз цих даних сприяє розвитку бережливого ставлення до навколишнього середовища, екології, формуванню критичного мислення, вміння вирішувати проблеми, критично оцінювати перспективи розвитку навколишнього середовища і людини. Можливі уроки на відкритому повітрі. При розгляді цієї лінії важливе місце займають відсоткові обчислення, функції, елементи статистики.

Наскрізна лінія «Громадянська відповідальність» сприяє формуванню відповідального члена громади і суспільства, що розуміє принципи і механізми функціонування суспільства. Ця наскрізна лінія освоюється в основному через колективну діяльність (дослідницькі роботи, роботи в групі, проекти тощо), яка поєднує математику з іншими навчальними предметами і розвиває в учнів готовність до співпраці, толерантність щодо різноманітних способів діяльності і думок.

Навчання математики має викликати в учнів якомога більше позитивних емоцій, а її зміст — бути націленим на виховання старанності, систематичності, послідовності, посидючості і чесності. З цієї ж наскрізною лінією пов'язані, наприклад, процентні обчислення, елементи статистики, що дозволяють учням зрозуміти значення кількісних показників при характеристиці суспільства і його розвитку.

Завданням наскрізної лінії «Здоров'я і безпека» є становлення учня як емоційно стійкого члена суспільства, здатного вести здоровий спосіб життя і формувати навколо себе безпечне життєве середовище.

Наскрізна лінія «Здоров'я і безпека» в курсі математики реалізується через завдання з реальними даними про безпеку і охорону здоров’я (текстові завдання, пов’язані з середовищем дорожнього руху, рухом пішоходів і транспортних засобів, відсотковими обчисленнями і графіками, що стосуються чинників ризику), перевищенням швидкості. Варто звернути увагу на проблеми, пов’язані із ризиками для життя і здоров’я при вивченні основ математичної статистики.

Наскрізна лінія «Підприємливість і фінансова грамотність» націлена на розвиток лідерських ініціатив, здатність успішно діяти в технологічному швидкозмінному середовищі, забезпечення кращого розуміння учнями практичних аспектів фінансових питань (здійснення заощаджень, інвестування, запозичення, страхування, кредитування тощо).

Ця наскрізна лінія пов'язана з розв'язуванням практичних задач щодо планування господарської діяльності та реальної оцінки власних можливостей, складання сімейного бюджету, формування економного ставлення до природних ресурсів. Вона реалізується під час вивчення відсоткових обчислень, рівнянь та функцій.

Формування універсальних навчальних дій з математики в умовах компетентнісного підходу до навчання

Що таке універсальні навчальні дії (УНД)?

УНД – це сукупність способів дії учня, що забезпечують його здатність до самостійного засвоєння нових знань і умінь, включаючи організацію цього процесу.

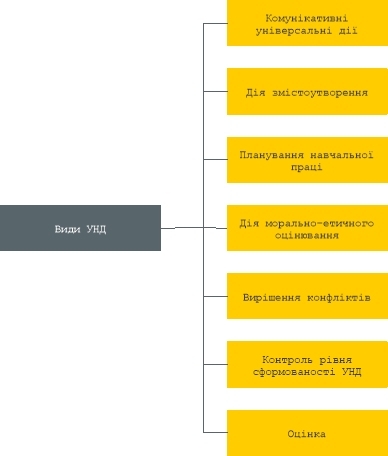
Рис. 1. Види УНД

Складові математичної компетентності

Математична компетентність - уміння бачити й застосовувати математику в реальному житті, розуміти зміст і метод математичного моделювання, вміння будувати математичну модель, досліджувати її методами математики, інтерпретувати здобуті результати, обчислювати похибки обчислень.

Таблиця 2. Складові математичної компетентності

Складова математичної компетентності	Характеристика
Дослідницька	формування задач на основі і деталізації, узагальненні, специфікації побудова комп’ютерної моделі задачі перевірка гіпотез за відомими методами власним досвідом систематизація здобутих результатів
Процедурна	алгоритм розв’язування задач відтворення тексту задач уміння систематизувати й розпізнавати типові задачі або зводити до відомої використання інформаційних джерел
Логічна	володіння й використовування апарату дедуктивних теорій удосконалення власних математичних уявлень дедуктивне доведення й обґрунтування розв’язування задач математична та логічна символіка на практиці
Технологічна	використання основних типів програмного забезпечення, електронних таблиць оцінювання похибки під час обчислення побудова комп’ютерної моделі задачі

Основна мета в освітній галузі «Математика»

Формування в учнів математичної компетентності;
Розвиток здатності чітко та аргументовано формулювати та висловлювати свої судження;
Забезпечення інтелектуального розвитку учнів;
Забезпечення розвитку їх уваги, пам’яті, логіки, культури мислення та інтуїції.

Приклад завдань

Знайдіть нулі функції

Скільки питань «ховається» в задачі?

Сформулюйте визначення нуля функції.
Що треба робити, для того щоб знайти нулі цієї функції?
Що означає розв’язати рівняння?
Що називають коренем рівняння?
Що треба врахувати при розв’язуванні цього рівняння?
Яка ОДЗ рівняння?
Може рівняння мати від’ємний корінь? Чому?
Сформулюйте умову нуля добутку.
Змініть рівняння так, щоб воно мало два корені.

Приклад задач з життя

Батьки разом зі своїм сином Андрієм проводили вихідний день у парку атракціонів. Відомо, що Андрій відвідав три різні атракціоні і за квитки було сплачено а грн. У таблиці наведено вартість дитячого квитка для кожного атракціону (у грн.) Оцініть значення а.

Найменування атракціону	Вартість одного дитячого квитка, грн.
Веселі гірки	15
Паровозик	14
Електричні машини	20
Карусель	10
Батут	12
Дитяча рибалка	8

Зовнішній діаметр порожнистої кулі 18см. Товщина стінок 3см. Знайдіть об’єм матеріалу, з якого виготовлено кулю.
Скільки оліфи треба, щоб пофарбувати зовнішню поверхню 11 однакових відер, які мають форму зрізаного конуса, якщо діаметри основ 25 см і 30см, твірна 27,5 см і на 1м2 витрачають 150 г оліфи?
Напівциліндричне склепіння підвалу має 6м довжини і 5,8м в діаметрі. Знайдіть площу повної поверхні підвалу.
З круглого листа металу ви штампували циліндричний стакан діаметром 25 см і висотою 50 см. Припустимо, що площа листа при штампуванні не змінилась. Знайдіть діаметр листа.
Стіжок сіна має форму циліндра з конічним верхом. Радіус його основи 2,5 м, висота 4 м, причому циліндрична частина стіжка має висоту 2,2 м. Густина сіна 0,03г/м3. Визначте масу стіжка сіна.
На малюнку зображений екран та каса кінотеатру. Зайняті місця позначені блакитним кольором. Встановіть, яка частина всіх місць в кінотеатрі: а) зайняті; б) вільні;

Індивідуалізація та диференціація навчання як умова формування базових компетентностей учнів на уроках математики.

Формування змістового компоненту математичної компетентності здійснюється на основі індивідуально – диференційованого підходу.

Індивідуалізація - організація процесу навчання на основі врахування індивідуальних особливостей учнів.

Диференціація - організація процесу навчання за декількома різними навчальними планами, програмами, завданнями в формі окремих груп, створених на основі врахування будь-яких узагальнених індивідуальних особливостей школярів.

Види диференціації:

рівнева;
профільна;

У основній школі головним видом диференціації є рівнева. Рівнева диференціація виражається у тому, що навчаючись в одному класі, за однією програмою та підручником, школярі можуть засвоювати матеріал на різних рівнях. Визначальним при цьому є рівень обов’язкової підготовки.

Індивідуальні завдання дозволяють учням:

достатньо оволодіти навичками розв’язування типових задач з теми;
проявити творчі здібності;
здійснювати саморозвиток і самоосвіту;
поліпшити оцінку з теми.

Профільна диференціація припускає навчання різних груп школярів за програмами, котрі відрізняються глибиною викладання матеріалу, обсягом відомостей і навіть номенклатурою питань, що вивчаються.

Формуванню життєвих компетентностей сприяє залучення учнів до:

виконання творчих завдань, написання наукових робіт, участь в інтелектуальних змаганнях (турніри, олімпіади, конкурси);
відвідування факультативних занять;
практикування диференційованих домашніх завдань та прийомів випереджувального навчання (розширення галузі знань предмета, просування до вищого рівня засвоєння знань з теми)

Прикладні задачі в шкільному курсі математики

Сутність прикладної спрямованості шкільного курсу математики полягає в орієнтації цілей, змісту і засобів навчання математики у напрямку:

здійснення цілеспрямованих змістових і методологічних зв'язків математики з практикою;
набуття учнями у процесі математичного моделювання знань, умінь і навичок, які будуть використовуватись ними у повсякденному житті, в майбутній професійній діяльності.

Прикладні задачі – один із дієвих і ефективних засобів для формування в учнів вмінь і навичок застосовувати набуті в шкільному курсі математики знання і вміння в нестандартних ситуаціях. Прикладна задача повинна відповідати таким вимогам:

питання задачі формулюється так, як воно зазвичай формулюється у житті;
розв’язок задачі демонструє практичне застосування математичних ідей у різних галузях;
зміст задачі повинен викликати в учнів пізнавальний інтерес;
дані та шукані величини задачі мають бути реальними, узятими з життя.

Радикальним методом реалізації прикладної спрямованості шкільного курсу математики є метод математичного моделювання.

Як же математики, оперуючи абстрактними поняттями, можуть так ефективно вивчати глибинні закономірності навколишньої дійсності?

Математики справді не вивчають живі організми, тверді тіла, рідини, гази, елементарні частинки, планети або галактики. Вони створюють математичні моделі досліджуваних об'єктів і відношень між ними (геометрія Евкліда, яку вивчають в школі, є математичною моделлю навколишнього тривимірного простору).

Реальним об'єктам простору зіставляються математичні абстракції, які відображають певні властивості реальних фізичних об'єктів, — точки, відрізки, прямі й інші плоскі та просторові геометричні фігури.

Математична модель — це опис якогось реального об'єкта або процесу мовою математичних понять, формул, рівнянь тощо, що є записами законів природи, які керують досліджуваним об'єктом чи явищем.

Процесу розв'язування будь-якої прикладної задачі властиві всі етапи математичного моделювання:

переклад задачі з природної мови тієї галузі, де вона виникла на мову.
математики (побудова математичної моделі);
розв'язування отриманої математичної задачі (дослідження математичної моделі);
записування математичного розв'язку з мови математики на мову тієї галузі, де вона виникла (інтерпретація розв’язків).

РОЗДІЛ 2. ЗАДАЧІ ДЛЯ ФОРМУВАННЯ КЛЮЧОВИХ КОМПЕТЕНТНОСТЕЙ

Математика і хімія

Скільки треба взяти грамів 6 % і скільки грамів 10 % розчину солі, щоб отримати 150 г 8% розчину?
Скільки кілограмів 20 % і скільки кілограмів 60 % сплавів міді треба взяти, щоб отримати 30 кг 30 % сплаву?
Скільки взяти грамів 4 % і скільки грамів 8 % розчину солі, щоб отримати 200 г 5 % розчину?
Скільки кілограмів 35 % і скільки кілограмів 50 % сплавів міді треба взяти, щоб отримати 30 кг 40 % сплаву?
У першому бідоні було молоко, масова частка жиру якого становить 3.
%, а в другому — вершки жирністю 18 %. Скільки треба взяти молока і скільки треба взяти вершків, щоб отримати 20 л молока з масовою часткою жиру 8 %?
У першому бідоні було молоко, масова частка жиру якого становить 2.
%, а в другому — 4 %. Скільки треба взяти молока з кожного бідона, щоб отримати 15 л молока з масовою часткою жиру 3 %?
Після того як змішали 60 % і 30 % розчини кислоти, отримали 400 г 50 % розчину. Скільки грамів кожного розчину змішали?
Після того як змішали 60 % і 20 % розчини кислоти, отримали 800 г 40 % розчину. Скільки грамів кожного розчину змішали?
Після того як змішали 30 % і 10 % розчини соляної кислоти, отримали 500 г 25 % розчину. Скільки грамів кожного розчину змішали?
Скільки кілограмів 30 % і скільки кілограмів 50 % сплавів олова треба взяти, щоб отримати 50 кг 45 % сплаву?
Морська сіль містить 6 % солі. Скільки прісної води треба долити до 30 кг морської води, щоб концентрація солі становила 2 %?
Змішали 20 % розчин і 40 % розчин сірчаної кислоти, отримавши 1000 г 25 % розчину. Скільки грамів кожного розчину взяли для цього?

Математика і біологія

Під час епідемії грипу серед обстежених в Львівській області 20 000 жителів виявили 9900 хворих. Оцініть імовірність події «навмання вибрана людина здорова».
Знаючи, що діаметр стовбура липи дорівнює 55см, учень обчислив площу поперечного перерізу стовбура, яка виявилась 2550,5 см2. Чи правильну відповідь він отримав? Якщо ні, то знайдіть правильну відповідь.
Гепард розвиває швидкість 34,5 м/с. Виразіть цю швидкість у кілометрах за годину, округліть до цілих та знайдіть абсолютну похибку наближення.
Знайдіть площу поверхні та об’єм кавуна, діаметр якого дорівнює 55 см.
Бактерія, потрапивши в організм, до кінця двадцятої хвилини ділиться на дві, кожна з них до кінця двадцятої хвилини знову ділиться на дві і т. д. Скільки бактерій буде в організмі через добу?
Найвищим з усіх дерев є секвоя, яка росте на Тихоокеанському узбережжі Північної Америки. Гігант на ім’я Гіперіон було знайдено 2006 року дослідниками М. Тєйлором і К. Аткінсоном. Ця секвоя росте в Національному парку Ретвуд у Каліфорнії, її висота становить 115,8 м. Пальма лодоіцея (сейшельська пальма) має дивовижні плоди. Вони схожі на величезне серце, розсічені надвоє вузької перетяжкою. Дозрілі плоди досягають півметра в діаметрі і мають середню масу близько 20 кг. Насіння цієї пальми найважчі і найбільші у всьому рослинному світі. Знайдіть середню масу насіння пальми лодоіцея, якщо вона становить близько 67 % від маси плода.
Американський тарган родом із тропічних районів Африки; районів Африки; 1625 року був завезений до Північної Америки і потім — до Європи. Живуть американські таргани як у будівлях, так і в дикій природі. Таргани завдають значної шкоди здоров’ю людини, є переносниками різних бактеріальних хвороб. Американський тарган є найшвидшою на планеті комахою. За одну секунду може пробігти відстань, що в 50 разів перевищує довжину його тіла. Для таргана ця швидкість становить 5,4 км/год. Чому дорівнює (у міліметрах) середня довжина американського таргана?
Черепахи — один із чотирьох загонів плазунів, що існує понад 220 мільйонів років. Вони поширені майже по всій Землі і живуть як у воді, так і на суші. Черепахи — довгожителі серед рептилій. Достовірно відомо, що Каролінська коробчата черепаха прожила в неволі 123 роки, середземноморська черепаха — 125 років, але рекордсменом є велетенська черепаха. Велетенська, або сейшельська гігантська черепаха — рідкісний вид сухопутних черепах. Вік найстаршого представника виду — черепахи Адвайта, яка померла 2006 року, оцінюють приблизно в 250 років. Укажіть приблизний рік народження черепахи Адвайта.
Найстарше дерево України — олива. Вона росте в Нікітському ботанічному саду в Криму. Її вік — приблизно 2100 років. На роль ще одного найстаршого дерева України претендує ялівець, якому близько 2000 років. Найстарше фісташкове дерево України теж росте в Нікітському ботанічному саду. Його приблизний вік — 1600 років. Дуб-Чемпіон — найстарший дуб в Україні. Він росте у селі Стужиця на Закарпатті. Його вік — приблизно 1250 років. У цьому ж селі росте «син» Чемпіона — Дідо-дуб. Його приблизний вік
- 1150 років. Найстарша липа України — липа Богдана Хмельницького в Золочівському районі на Львівщині. Дереву близько 700 років. Побудуйте стовпчасту діаграму, яка відображає вік найстарших дерев України.

Попереднім рекордсменом була секвоя під назвою «Стратосферний гігант» висотою 112,8 м. Скільки відсотків висоти Гіперіона складає висота Стратосферного гіганта? Результат округліть до сотих.

Кульбаба — це багаторічна трав’яниста рослина родини айстрових. Її висота досягає 30-40 см, довжина листя — до 20 см, на кожній рослині буває приблизно 6 квіток. У кульбаби велика здатність розповсюджуватися. Одна квітка дає до двохсот насінин. (Кожна кульбаба займає площу приблизно 20 см2; якби всі рослини виживали, то до десятого покоління знадобилася б площа в 15 разів більша, ніж поверхня земної кулі.) Але не з усіх насінин виростають кульбаби, більшість їх гине. Скільки виросте кульбаб з однієї рослини, якщо проросте все насіння?

Математика та географія

Населення міста за два роки збільшилося із 60 000 мешканців до 64100. Знайдіть середній щорічний відсоток приросту населення в цьому місті.
Користуючись діаграмою, у якій відображено зміну чисельності населення України за роками, назвіть: 1) Рік, коли була найбільша чисельність населення. 2) Рік з найменшою чисельністю населення. 3) У якому з років, 1993 чи 1995, чисельність населення була більшою?

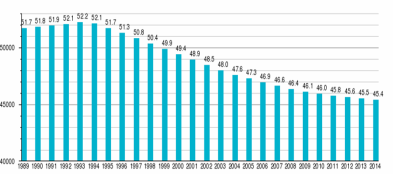
Географічний атлас — це збірник географічних карт планети або деякої частини планети (зазвичай планети Земля). Але існують також атласи для інших планет Сонячної системи та їх супутників. Перша книга, яка може бути названа атласом, складена давньогрецьким ученим Клавдієм Птоломеєм приблизно 150 року н. е. Перше видання було опубліковане в Болоньї 1477 року. Скільки років минуло від створення до опублікування цього атласу?
Марганцеві руди — вид корисних копалин, їх використовують у чорній металургії для виробництва рейкової сталі, а також у виробництві скла, кераміки, мінеральних барвників. Україна володіє найбільшими у світі запасами марганцевої руди, що становить 2,3 млрд тон, або 11 % світових запасів. Яка кількість (у тонах) світових запасів марганцевої руди?

Задачі економічного змісту

Вкладник поклав до банку на два різні рахунки загальну суму 15 000 грн. За першим із них банк виплачує 6% річних, а за другим — 8 % річних. Через рік вкладник отримує 1000 грн відсоткових грошей. Скільки гривень він поклав на кожен рахунок?
Вкладник поклав до банку 5 000 грн. За перший рік йому було нараховано певний відсоток річних, а другого року банківський відсоток було зменшено на 3 %. У кінці другого року на рахунку було 8600 грн. Скільки відсотків становила банківська ставка в перший рік?
Вкладник поклав до банку 7 000 грн. За перший рік йому було нараховано певний відсоток річних, а другого року банківський відсоток було збільшено на 2 %. У кінці другого року на рахунку було 9640 грн. Скільки відсотків становила банківська ставка у перший рік?
Вкладник поклав до банку 8 000 грн. За перший рік йому було нараховано певний відсоток річних, а другого року банківський відсоток було збільшено на 4 %. У кінці другого року на рахунку було12332 грн. Скільки відсотків становила банківська ставка в перший рік?
Вкладник поклав до банку на два різні рахунки загальну суму 12000 грн. За першим із них банк виплачує 10% річних, а за другим — 8 % річних. Через рік вкладник отримує 1000 грн відсоткових грошей. Скільки гривень він поклав на кожен рахунок?
Вкладник поклав до банку 11 000 грн. За перший рік йому було нараховано певний відсоток річних, а другого року банківський відсоток було збільшено на 2 %. У кінці другого року на рахунку було 13 880 грн. Скільки відсотків становила банківська ставка у перший рік?
Телевізор коштує 15000 грн. Скільки він коштуватиме, якщо його ціна знизиться на 2%?
Шкільна форма коштувала 1600грн. Перед початком навчального року ціна підвищилась на 7%. Скільки стала коштувати шкільна форма?
На передріздвяному розпродажі ціна на холодильники знизилась з12600 грн до 11800 грн. На скільки відсотків знизилась ціна?
До підвищення цін товар коштував 240 грн. Знайдіть ціну товару після двох послідовних підвищень, якщо першого разу підвищили на 10%, а другого - на 7%.

Математичні задачі з інформаційним матеріалом екологічного змісту

Для виробництва 4000м3 паперу вирубують 1га лісу. Скільки вирубали лісу, щоб надрукувати підручник «Математика 5 клас» для всіх учнів вашого класу.
Листяний ліс, площа якого 1га, може за рік затримати 68 т пилу. Порахуйте скільки пилу залишилось в повітрі, через видавництво вашого підручника.
Щотижня кожна родина викидає не менше двох відер сміття. Скільки сміття назбирає родина за рік, якщо в році 52 тижня? Скільки це у кілограмах, якщо у відрі 10кг?
Скільки сміття викинуть жителі нашого селища Квасилів, якщо у нас проживає близько 3700 сімей? Скільки потрібно тракторів, щоб вивезти це сміття, якщо на трактор можна навантажити 3т сміття?
Одне горнятко кави вимиває з організму людини 40 мг кальцію. Для дитячого організму шкідливою є втрата 0,16 г кальцію в день. Учень 9 класу випив три горнятка кави за день. Чи наніс він шкоду своєму організму?
Кожна викурена цигарка скорочує життя підлітку на 6 хвилин. На скільки часу скоротив собі життя підліток, який викурює за добу 3 цигарки, якщо «стаж курця» 2 роки ? Скільки грошей міг би зекономити учень, якщо у пачці 20 цигарок і коштує вона 30 гривень?
Норма добової потреби учнів Львівської області (згідно з регі- ональними потребами) у різних вітамінах у середньому становить 130 мг. Одна цигарка знищує 20 % вітамінів. Скільки мг вітамінів краде в себе той, хто щодня викурює 5 цигарок?
Установлено, що 1 га парку очищує за рік 18 млн м3 повітря. Скільки метрів кубічних повітря очистить парк, площа якого 22,77 га?
Скільки вуглекислого газу вбирають насадження парку і скільки при цьому виділяють кисню, якщо 1 га зелених насаджень вбирає за добу 280 кг вуглекислого газу, виділяючи про цьому 220 кг кисню?
Запаси води на нашій планеті становлять 1800 млн км3. На світовий океан припадає 98 %. Прісна вода становить 2 %, з них тільки 1 % перебуває в рідкому стані. Скільки води кожного виду є на землі?
У класній кімнаті 10 лампочок по 100 Вт кожна. Якщо вони горітимуть марно 1 годину, то буде втрачено 1 кВт/год електроенергії. У нашій гімназії 10 класних кімнат. Чому дорівнюватимуть втрати електроенергії в межах гімназії?

Щороку землі України втрачають близько 24 млн. т гумусу. Підрахуйте, скільки гумусу втрачається на території сільськогосподарського кооперативу, якщо площа орних земель 1200 га? Площа орних земель України
- 33 080 тис. га.
Якщо учень нашої школи збереже за чверть один зошит, країна збереже від вирубування 45 га лісу. Яка площа лісу буде збережена, якщо кожний учень за рік збереже 6 зошитів? У школі навчається 986 учнів.
Один гектар полезахисної смуги шириною 10м захищає поле площею 25-30 га та на кожному гектарі сприяє збільшенню врожаю на 3-4 ц. На скільки центнерів збільшиться врожай на всій захищеній площі?
Як зміниться кількість вуглекислого газу на кінець уроку, якщо в кімнаті 28 чоловік і кожен з них у середньому протягом однієї хвилини виділяє у процесі дихання 250 мл СО2.
На побутові потреби за добу в середньому витрачається 250 л води (для м. Києва). Вирахуйте, скільки витрачатиметься води за місяць (рік)?
Обчисліть, скільки енергії було витрачено при написанні контрольної роботи, враховуючи такі дані: під час писання на 1 кг маси людина витрачає 6,3 кДж на 1 год.
За одну годину двигун вантажного автомобіля "МАН" в холостому режимі спалює 25л палива. Скільки палива витратить він, якщо працюватиме в холостому режимі 0,5 год.; 1,5 год.?
Цівка води товщиною в сірник дає за добу втрату 480 л. Скільки води буде втрачено, якщо 100 чоловік не до кінця закрутять крани ? Скільком жителям вистачить цієї води на добу, якщо мінімум використання води для однієї людини 6л?

РОЗДІЛ 3. ФРАГМЕНТИ РОЗРОБОК УРОКІВ ТА ПОЗАКЛАСНИХ ЗАХОДІВ

Урок математики 6 клас

Тема. Розподільна властивість множення. Зведення подібних доданків.

Мета: завершити роботу з відпрацювання навичок використання розподільної властивості множення для: а) обчислень; б) розкриття дужок; в) зведення подібних доданків; г) винесення найбільшого спільного множника за дужки. Розвивати обчислювальні навики, розумову активність, логічне мислення, інтерес до вивчення математики. Сприяти вихованню позитивного ставлення до навчання.

Тип уроку: урок удосконалення знань, умінь і навичок.

«А коли добре щось умієте – того не забувайте, А чогось не вмієте – того учітеся» Володимир Мономах (1117р.)

Хід уроку

Організаційний етап

Привітання:

- «Доброго дня, діти! У нас сьогодні багато гостей – розкажіть їм про себе.»

- «Ми веселі, кмітливі, допитливі! Ми вчимося, пізнаємо, творимо! Ми хочемо знати все!»

Перевірка готовності учнів до уроку

Перевірка домашнього завдання

-Які запитання виникли при виконанні д\з?

-Якими правилами ви користувалися?

Математична скринька знань з теми:

Модуль числа

Додавання двох від’ємних чисел:

-а +(-в) =-(| а | + | в |)

Додавання чисел з різними знаками:

а + (-в) = +| а | - | в |, якщо | а | > | в |

а + (-в) = -| в | - | а |, якщо | в | > | а |

Віднімання:

а – в = а + (- в)

Множення двох від’ємних чисел:

- а · (-в) = | а | · | в |

Добуток чисел з різними знаками:

(- а ) · в = - | а | · | в|

III. Оголошення теми і мети уроку.

«Продовжимо наш урок казкою «Пряник і колосок», яку написав своєму сину відомий педагог В.О. Сухомлинський.

Вранці, до сходу сонця Людина взяла білий пряник і пішла в поле. Зірвала колосок у полі, вийняла із нього зернята, і спробувала на зуб, посміхнулася і заховала колосок у кишеню. Ось там і зустрілися Пряник і Колосок.

- Хто ти такий? – запитав Пряник

- Я Колосок.

- Ой, який ти колючий! Яка з тебе користь?

Посміхнувся колосок, поворухнув своїми вусиками і відповів:

- Без мене не було б ні хліба, ні тебе, Прянику.

- Отже, - каже Пряник, все від тебе. Але хто ж над тобою старший?

- Праця, - відповідає Колосок, - вона все дає. Але праця в руках людини. Праця і Людина – найголовніше.

Отже, я вас закликаю до наполегливої праці, щоб пізнати істину міркувань.

Сьогодні ми продовжимо працювати над темою «Розподільна властивість множення. Зведення подібних доданків»; розвиватимемо логічне мислення та навички колективної і самостійної роботи. Сподіваюся, що кожен виявить глибокі знання, доведе свою ерудованість у світі раціональних чисел, в кінці уроку виконаємо перевірку знань.»

IV. Відпрацювання навичок

Гра «Вірю-не вірю» (Математична розминка)

Чи виражає рівність розподільну властивість множення (а+в)с=ас+вс?

Чи є заміна виразу ас+вс виразом (а+в)с — винесення спільного множника за дужки?

Усні вправи

13-(-6) -6∙ 5-89+89

5,8+7,8-45+567 -8∙ (-9)

-5-(-67)

56+(-78)

6∙ (-10)

-3,8+(-7,8)

-0,4∙ 3 0∙ (-1,2)

Завдання класу

№1282(1)-фронтально

Обчисліть, застосовуючи розподільну властивість множення:

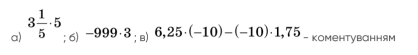
Усні вправи

Поставити перед дужками «+» або «-», щоб рівність була правильною:

... (-10 а+ 6) = -10а + 6
...( р –с+ п ) = -р+с-п
... ( -4 + 5х ) = 4-5х
...(-17а + 8в) = 17а -8в
... (х+ у-с) = х+у-с

Розкрити дужки:

5(2а+6);
-9(3в -4);
-1/7(21х+49)

Спростіть вираз:

№1396(2)- фронтально

Усні вправи

Знайти корінь рівняння:

0,34∙х=0
х-7,1=4,5
-7│х│=0
х꞉(-10)=3,4

Розв’язати рівняння:

а)7x +41x =192;
3( 5х -8) =36 ;
-2,4х│х-8│(3х-23)=0

Задача

Я задумав число. Якщо його збільшити на 20, а результат помножити на 6, то отримаємо 150. Яке число я задумав?

Вправа на уважність

Вправа «Детективне агентство» (Основне завдання для «Детективних агентств» - скласти фоторобот крадія, виконавши 6 завдань на додавання, віднімання та множення раціональних чисел, правильні відповіді – основні прикмети зовнішності. Використовуючи кольорові олівці та результати роботи, відобразити фоторобот на листку паперу.)

Форма обличчя:

Розв’яжіть рівняння 3,16 + х = 1,53

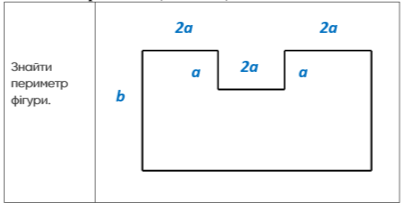
а) 2,07; овальне б) -1,63; кругле в) 5,13; витягнуте г) – 5, 13; квадратне

Колір очей:

Обчислити: 8-7+9-8

а) 22; зелені б) – 2; карі в) 2; блакитні г) – 15; чорні

Волосся:

Порівняйте числа: - 6,78 і - 9,24

а)перше менше за друге – чорні прямі

б) перше більше за друге – руді прямі

в)перше дорівнює другому – світлі хвилясті

г) не можна визначити – чорні кучеряві

Форма носа

Скільки цілих чисел розташовано на координатній прямій між числами – 5 і 5?

а) 11; картоплею б) 10; кирпоносий

в) 8; з горбинкою г) 9; прямий

Губи:

Розв’яжіть рівняння– 4 - х = - 2

а) 2; бантиком ; б) - 2; вузькі; в) 6; пухкі; г) - 6 ; куточки опущені вниз.

Особливі прикмети

Розв’яжіть рівняння /х/ - 7 = 12

а) х=19; світлі пишні вуса б) х = - 19; родимка на лівій щоці

в) х1 = 19; х2 = - 19; х3 = - 5; маленька чорна борідка

г) х1 = 19; х2 = - 19; чорні вусики

Прикмети Зловмисника: кругле обличчя, блакитні очі, руде волосся, прямий ніс, вузькі губи, чорні вусики.

V. Діагностика рівня засвоєння навчального матеріалу

Тестові завдання

Варіант 1

1. Який результат дістанемо, застосувавши розподільний закон множення для обчислення виразу (0,03 + 2,5) · 0,4?

1) 1,12; 2) 10,12; 3) 1,012; 4) 2,12.

2. Який вираз дістанемо, розкривши дужки в добутку -5р(-х + 2у – 3k)?

1) -5хр + 10ру - 15рк;

2) 5рх - 10ру +15рк;

3) 5рх - 10рх - 15рк;

4) 5рх -2ру + 15рк.

3. Який вираз дістанемо, спростивши вираз 4с(3а – 2) – 6а(2с + 1)?

1) 12aс – 8с + 12ас + 6a; 2) -8с - 6а; 3) -8с + 6a; 4) 8с - 6а.

4. Обчисліть значення виразу 5·(5p – 4х) – 4·(х – 2p), якщо p = -2; х = 2.

1) -18; 2) -114; 3) -90; 4) 90.

Варіант 2

1. Яке з поданих чисел дістанемо, застосувавши розподільний закон множення до виразу (12,5 + 0,1) · 0,8?

1) 100,8; 2) 18; 3) 10,8; 4) 10,08.

2. Який вираз дістанемо, розкривши дужки в добутку -2k(3а – 5b – 2с)?

1) 6ak - 10bk – 4ck;

2) 6ак +10bk + 4ck;

3) -6ak + 10bk + 4ck;

4) -3аk – 5bk – 4сk.

3. Який вираз дістанемо, спростивши вираз 5p · (-3 + k) – k · (5p – 1)?

1) -15p - k; 2) 15р – k; 3) -15р + k; 4) -15р + 5рk + 5рk – k.

4. Обчисліть значення виразу (2х - 3у) – 2·(5х - 2у), якщо х = -1, у = 1?

1) -9; 2) 1; 3) 9; 4) -1.

VІ. Підбиття підсумків уроку

Запитання до класу

1.Де ми використовували розподільну властивість множення?

2. Чим відрізняються подібні доданки один від одного?

3. За якої умови добуток дорівнює нулю?

Рефлексія

Відзначте на промені, де ви знаходитеся після уроку

0, якщо не умієте помножити раціональні числа

1, якщо умієте

«Те, що я встиг пізнати – чудово. Сподіваюся, таке ж чудове те, що мені ще доведеться пізнати » Сократ, давньогрецький філософ

VIІ. Домашнє завдання, інструктаж щодо його виконання.

Фрагмент уроку алгебри

Тема: Прогресії та їх застосування

Мета: формувати навики використовувати означення, властивості та формули арифметичної та геометричної прогресій при розв’язуванні вправ. Формувати вміння вирішувати життєві проблеми, аналізувати, прогрозувати, ухвалювати оптимальні рішення; учити учнів аналізувати та оцінювати досягнення світової культури та історії.

Математика цікава тоді, коли живить нашу винахідливість і здатність міркувати. Д. Пойа

Недостатньо мати добрий розум, головне – це раціонально його застосовувати. Р. Декарт

З історії виникнення поняття числової послідовності

Фрагменти позакласних заходів

Не навчайте дітей так, як навчали вас, бо вони народилися в інші часи. Народна мудрість.

Інтелектуальна математична гра «Хто зверху?»

Мета: прищеплювати любов до математики, виробляти вміння використовувати здобуті теоретичні знання на практиці; розвивати пізнавальні здібності учнів, інтерес до математики як до науки, творчу активність, вміння швидко та раціонально приймати рішення, логічно мислити, працювати в команді.

Хід гри

Ведуча. Доброго дня! Ми вітаємо Вас на інтелектуальній математичній грі - конкурсі «Хто зверху?»! Хто розумніший - чоловіки чи жінки? Тисячі років людство шукає відповідь на це філософське питання. І сьогодні ми дамо відповідь на це запитання. Отже, Вітаємо команди дівчат, хлопців та глядачів. Давайте домовимось – за мною об’єктивність, за Вами – цікавий двобій ерудованості, логіки, інтелекту. І нехай переможуть найсильніші!

Пояснення: У грі беруть участь дві команди — хлопців та дівчат. Дуель команд дівчат і хлопців ділиться на чотири раунди, що складаються з різних конкурсів. Переможець визначається у фінальному, шо раунді, де бали переможця зростають удвічі.

Отже, починаємо, перший раунд.

Раунд 1

«Збери літери»

Ведуча. На одяг гравців прикріплені аркуші, на яких написані літери. Гравцям потрібно з цих літер скласти слова, що є відповідями на поставлені запитання. Відповідь зараховують, якщо гравці вишукувалися в ряд, і слово читається правильно. Правильна відповідь оцінюється в 1 бал. На все дається 2 хвилини.

Запитання для дівчат:

(К, Д), (Р, Т), (У, А), (Г, И)

1) Вони бувають суміжними, вертикальними, відповідними. (Кути)

2) Що об’єднює хронологічну таблицю з історії з математикою? (Дати)

3) Буває, що коли виконують домашнє завдання, то до математики вони не доходять? (Руки)

4) Яке слово пропущене в прислів’ї: «Куди голова задумала, то… й ноги несуть»? (Туди)

Запитання для хлопців:

(Т, О), (І, К), (Л, Р), (О, Д)

1) Фігура, що складається з усіх точок площини, рівновіддалених від однієї точки. (Коло)

2) Пора року, коли можна відпочити від математики. (Літо)

3) Про виконання домашнього завдання з математики говорять приказку: «Зробив … - гуляй сміло» (Діло)

4) Як можна назвати одним словом трьох учнів, які розв’язують задачі біля дошки? (Тріо)

Бонусне запитання: правильна відповідь оцінюється в 1 бали.

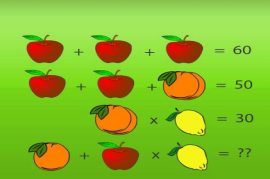
Відповідь. 65

Ведуча. Пані Справедливість, скільки балів одержали команди?

Суддя. Рахунок__________ На користь_______.

Раунд 2

«Вірю - не вірю»

Ведуча. Другий конкурс «Вірю - не вірю». Кожній команді по черзі читатиму твердження, а члени команди повинні вирішити – правдиве воно чи ні. За кожне правильно вгадане твердження команда отримає 1 бал. Час відгадування – 3 хвилини.

Ведуча. Твердження для команди дівчат:

1. Вірите, що Шарль Перро, автор «Червоної шапочки», написав казку «Любов циркуля та лінійки»? (так, є така казка)

2. Вірите, що іспанського математика Паоло Вальмеса за те, що він розв'язав рівняння четвертого степеня, спалили на вогнищі. (Так. Він був першою людиною, яка змогла розв'язати рівняння четвертого степеня)

3. Чи вірите ви, що кути паралелограма, прилеглі до однієї сторони дорівнюють 40º і 120º? (Не вірю, сума внутрішніх односторонніх кутів дорівнює 180º).

4. Чи вірите ви, що у довільного рівнобедреного трикутника з кутом 60º бічна сторона дорівнює основі? ( вірю)

5. Лінійне рівняння завжди має лише один корінь? (Ні)

6. Фалес був уболівальником і помер на трибуні Олімпійського стадіону під час бою Піфагора? (Так)

7. Бісектриса трикутника ділить протилежну сторону навпіл? (Ні)

Ведуча. Твердження для команди хлопців:

1. Чи вірите ви, що Рене Декарт першим запропонував метод нумерації крісел в театрі по рядах і місцях? (Так. Аристократи-театрали, навіть, просили короля нагородити вченого, та король відповів: Так, те, що винайшов Декарт - чудово, так, це заслуговує на орден! Але дать його філософу!? Ні, це вже занадто!)

2. Чи вірите ви, що якщо кожного дня по десять годин переписувати праці Леонардо Ейлера, не вистачить і 76 років? (Так. Зібрання його праць становлять 75 великих томів. Про нього говорили, що він «рахує так, як люди дихають)

3. Вірите, що Піфагор приймав участь в кулачному бою на 58 Олімпіаді? (Так. Він був чемпіоном з цього виду спорту)

4. Будь-який прямокутник має рівні діагоналі. (Так)

5. Квадрат від’ємного числа є числом від’ємним. (Ні)

6. Найменше натуральне число нуль? (Ні)

7. Сума гострих кутів прямокутного трикутника дорівнює 90∘. (Так)

Бонусне запитання: Які математичні знаки пропущені?

Відповідь. +++

Ведучий. Пані Справедливість, скільки балів одержали команди?

Суддя. Я дізналася дуже багато цікавих фактів, і рада вашим успіхам.

Рахунок__________ На користь_______.

Раунд 3

«Хто я?»

Ведуча. Зараз ми переходимо до конкурсу «Хто я?». Один із гравців команди отримає картинку, правда він її бачити не буде (бачитимуть зображення члени команди, воно буде спроектоване на екран позаду учасника ), на якій може бути предмет, або людина, які мають відношення до математики..

Завдання учасника - вгадати, що це за предмет чи персонаж, ставлячи до членів команди запитання, на які вони можуть відповідати лише «так» або «ні». Час на відгадування – 2 хвилини.

Почнемо з хлопців. Кого з «орлів» дівчата хочуть бачити? (Команда відгадує картинку із зображенням транспортира).

Ведуча. Кого з красунь вибирають хлопці для участі в конкурсі? (Команда відгадує картинку із зображенням циркуля)

Ведуча. Пані Справедливість, хто Вам у цьому конкурсі сподобався більше? Ну і скільки у нас балів?

Бонусне запитання:

Яка тінь відповідає малюнку?

Відповідь. 5

Якій команді бонусне запитання принесли додаткові бали?

Раунд 4

«Бліц»

Ведучий. Наш наступний конкурс «Бліц». Я буду ставити запитання і за 2 хвилини команда має дати якомога більше правильних відповідей. Відповідь має бути лаконічною «Чоловік» або «Жінка».

Ведуча. Я думаю, Ви не проти, якщо ми розпочнемо з дівчат. Отже, дорогенькі дівчатка Ваша хвилина пішла.

1. Чотирикутник, сторони якого попарно паралельні? (чоловік, паралелограм)

2. Числовий множник, що стоїть перед буквеним виразом? ( чоловік, коефіцієнт.)

3. Найбільша сторона прямокутного трикутника? (Жінка, гіпотенуза)

4. Назва якої держави ховається в математичному виразі а³ ( а в третьому степені)? (Жінка, Куба)

5. Пів-пряма, яка має початок, але не має кінця? (чоловік, промінь)

6. Результат дії додавання? (жінка, сума)

7. Відрізок, що сполучає вершину і середину протилежної сторони трикутника? (жінка, медіана)

Ведуча. Хлопці, ви готові? Час пішов.

1. Чотирикутник, у якого тільки дві сторони паралельні? (жінка, трапеція)

2. Вимірюється в квадратних метрах? (жінка, площа)

3. Прилад для вимірювання кутів? (чоловік, транспортир)

4. Яка геометрична фігура потрібна для покарання дітей? ( чоловік, кут)

5. Що є спільного у словах, рослинах і рівняннях? (чоловік, корінь)

6. Яку математичну фігуру носять на голові чоловіка? (чоловік, циліндр)

7. Результат дії множення (чоловік, добуток)

Ведуча. Пані Справедливість, хто у цьому конкурсі був кращим?

Суддя. Рахунок__________ На користь_______.

Ведуча. Пані Справедливість, Вам слово!

Бонусне запитання:

Відповідь. 50

Суддя. Рахунок__________ На користь_______

Фінал

Ведуча. Щоб остаточно визначити переможця проведемо гру – показуха. Кожна команда одержить по 3 математичних терміни, які потрібно показати

1. Трапеція, вершина, бісектриса;

2. Ромб, радіус, висота.

Ведуча. Пані Справедливість, Вам слово!

Суддя. Перемогу святкують ______________________.

Їх рахунок подвоюється.

Але я хочу сказати, що сьогодні перемогла наука. Ми побачили, що знання нам потрібні завжди і всюди – чи то ми хлопці, чи дівчата. Знання потрібні кожній людині, незважаючи на її стать, адже гендерна рівність – запорука розвинутого суспільства. Рівноправна участь жінок і чоловіків у всіх сферах життєдіяльності суспільства та держави є важливою умовою й гарантією утвердження демократії в Україні та запорукою її європейської інтеграції.

Інтелектуальна гра «Все є число» (Піфагор)

Мета:

сприяти різносторонньому розвитку учнів, зміцненню їх знань з природничих дисциплін, виникненню внутрішніх мотивів навчання, вибору подальшої профілізації навчання; показати зв`язок математики з іншими науками;
активізувати розумову діяльність учнів; психологічно розвантажити учнів, що відчувають певні труднощі при вивченні предметів природничого циклу;
забезпечити активність, зацікавленість учнів; виховувати інтерес до вивчення точних наук. сприяти підвищенню загальної культури учнів.

Форма проведення: гра - змагання.

Обладнання:

1. Плакати з висловами:

«Ніколи не соромся питати про те, чого не знаєш» (арабська мудрість)
«Хто з дитячих років займається математикою, той розвиває увагу, тренує свій мозок, свою волю, виховує в собі наполегливість у досягненні мети» (А.І.Маркушевич)
«Радість бачити й розуміти є найпрекраснішим даром природи» (А.Ейнштейн)
«Знання збираються по краплині, як вода в долині» (українське прислів`я)

2. Нагороди:

за перемогу у шкільному марафоні;
за різносторонній розвиток особистості;
за рівень знань з природничих дисциплін;
за інтерес до вивчення точних наук;
за оригінальність математичної думки;
за наполегливість у досягненні мети.

План

1. Вступне слово вчителя.

2. Доповідь - бесіда по темі вечора.

3. I тур «Розминка»

4. Казка – головоломка " Сімнадцять верблюдів"

5. II тур «Своя гра»

6. Математичні фокуси:

а) "Скільки вам років?";

б) "Живий арифмометр";

7. ІІІ тур «Поміркуємо логічно»

8. Вікторина для вболівальників

9. Гра «Ой, не можу!»

10. ІV тур «Це моя точка зору»

11. "Математичні танці"

12. V тур“Показуха”

13. Весела перерва

14. Виступ журі. Нагородження учасників і переможців

Доповідь - бесіда по темі вечора.

1-й ведучий. Ми живемо в 3 тисячолітті! В час визначних відкриттів і досягнень людства. Ми багато що знаємо, багато що уміємо. Нам відомий вислів старогрецького математика, філософа, що жив у VI ст. до н.е. – Піфагора – «Все є число». Значить, як у минулому, так і в майбутньому, без математики не обійтися.

Відеозапис «Історія виникнення чисел»

2-й ведучий. Звучить музика, і здається, що може бути спільного між математикою і музикою, між сухими формулами і божественними звуками? А виявляється, є. Ви замислювалися коли-небудь над тим, що за предмет – математика? Ось, наприклад, що вивчає астрономія?

1-й ведучий. Зірки.

2-й ведучий. Вони реально існують?

1-й ведучий. Так.

2-й ведучий. Що вивчає біологія?

1-й ведучий. Навколишній світ, тварин, рослин.

2-й ведучий. Вони реально існують?

1-й ведучий. Так.

2-й ведучий. Що ж вивчає математика?

1-й ведучий. Числа. Геометричні форми.

2-й ведучий. Вони реально існують? До них можна доторкнутися?

1-й ведучий. Ні.

2-й ведучий. Значить, математика займається речами, яких насправді немає?!

1-й ведучий. Значить, це наука, існуюча тільки в людських думках. Наука, створена розумом людини. І здається чимось надприродним, бо за допомогою формул можна розрахувати політ космічного корабля, «економічну ситуацію» в країні, погоду «на завтра», описати звучання нот в мелодії.

2-й ведучий. „Предмет "математика" настільки серйозний, що корисно не упускати випадку зробити його трохи цікавим", - писав видатний учений XVII століття Паскаль. І хоча математика здається багато чим серйозною, і навіть нудною наукою, іноді і в ній прослизає пустотлива усмішка.

Відеопрезентація «Математика навколо нас»

1-й ведучий. В математиці відвіку існують жартівливі задачі. Але вирішують їх люди не тільки ради розваги. Іноді задача-жарт дозволяє глибоко проникнути в суть правил, краще запам'ятати.

2-й ведучий. Щоб відразу настроїтися на математичний лад, вирішимо таку задачу: треба довести, що 2=1. Очевидно, що а2 – а2 = а2 – а2 . Ліву частину розкладемо по формулі різниці квадратів, а з правої винесемо загальний множник за дужки.

Одержимо (а – а) (а + а) = а (а – а), скоротивши, тобто поділивши обидві частини рівності на (а – а), одержимо а + а = а, тобто 2а = а або 2 = 1

Де була помилка? (до глядачів). Чому вийшло така безглуздість? Яке правило порушено? (а – а = 0, на нуль ділити не можна, а ми розділили)

1-й ведучий. А скільки в математиці загадкових курйозів! Ось, наприклад, якщо ми зробимо найгрубішу помилку і скоротимо дроби і просто закреслюючи цифру 6 в чисельнику і в знаменнику, одержимо… вірну відповідь!!!

2-й ведучий. А ось курйоз, пов'язаний з властивостями числа 12345679. Якщо його помножити на 9, то в результаті вийде число, записане тільки цифрою 1. Якщо помножити на 18, то вийде число записане, тільки 2, а якщо помножити на 27, як думаєте, якою цифрою буде записано одержане число? Вірно, цифрою 3.

1-й ведучий. Є числа з вельми цікавими властивостями. Якщо, наприклад, число 12 записати навпаки – 21, то квадрат знов даного числа виявиться квадратом числа, також записаного навпаки: 12² = 144, а 21² = 441.

2-й ведучий. Ще один цікавий факт: існує всього три числа, рівні сумі своїх цифр, піднесених до степеня, рівного їх кількості. Ось вони 81;512;2401

81 = (8+1)²; 512 = (5+1+2)³; 2401 = (2+4+0+1)⁴.

1-й ведучий. Не тільки руки, ноги і тіло вимагає тренування, але мозок людини вимагає вправ. Рішення задач, головоломок, математичних ребусів, розвиває логічне мислення, швидкість реакції. Недаремно говорять, що математика - гімнастика розуму. Так давайте сьогодні і займемося цією математикою.

2-й ведучий. Зараз кожний з вас може перевірити свою увагу, пам'ять, уміння логічно мислити. Хотілося б, щоб після сьогоднішньої зустрічі ви інакше подивилися на математику, відчули її красу і більш глибоко усвідомили необхідність її вивчення.

Тим, хто вчив математику,

Тим, хто вчить математику,

Тим, хто буде вчити математику,

Тим, хто ще не знає,

Що може любити математику

Сьогоднішній турнір присвячується!

1-й ведучий. Доброго дня, дорогі друзі! Ми ради вітати вас на нашій грі! Сьогодні ми розпочинаємо шкільний інтелектуальний марафон!

2-й ведучий. Ви можете сказати, що марафон – це щось спортивне. Дійсно, марафон названий на честь еллінського воїна, який прибіг в Афіни з містечка

Марафон зі звісткою про перемогу над персами.

1-й ведучий. А наш марафон – інтелектуальний. На всіх гравців чекають складні випробування, причому з різних наук. Сподіваймося, що звістка про переможців нашого марафону швидко рознесеться по всій школі. А зараз зустрічаємо наших марафонців!

2-й ведучий. У грі приймають участь учні 7 – 9 класів. Привітаємо їх! ...

1-й ведучий. І нехай пані Фортуна визначить найрозумнішого учня школи!

А щоб їй допомогти, представляємо наше журі: ...

І тур. «Розминка»

Умови конкурсу:

У першому турі гравці відповідають на 10 запитань, ставлячи літеру відповіді, яку вони вважають правильною в оціночний бланк після того, як ведучий прочитає запитання.

За правильну відповідь надається 1 бал.

Завдання для конкурсу «Розминка»

1. Одиницею маси є:

а) 1ц; б) 1л; в) 1км; г) 1а.

2. Кут, градусна міра якого 30º, називається:

а) тупим; б) прямим; в) гострим; г) розгорнутим.

3. Хто з наступних відомих математиків, зробивши неоціненний внесок в її розвиток, є нашим співвітчизником?

а) Піфагор; б) Лобачевский; в) Остроградський; г) Декарт.

4. Чому дорівнює площа квадрата зі стороною 10 см?

а) 40 см; б) 100кв.см; в) 80м; г) 60см. кв.

5. Наші пращури для вимірювання маси тіла використовували інші одиниці, ніж ми. Назви деяких нам відомі і зараз. Але означають вони інше. Раніше гривня була не грошовою одиницею, а мірою маси тіл. Яка вага гривні?

а) 25кг; б) 400г; в) 16кг; г) 4г.

6. Яке число вважалося раніше щасливим?

а) 1; б) 2; в) 7; г)12

7. Одиницею часу є:

а) 1км/год; б) 1 доба; в) 1см; г) 1а.

8. Скільки граней має новий шестигранний олівець?

а) 8; б) 6; в) 3; г) 12.

9. Мінімальний елемент зображення монітора комп`ютера:

а) байкер; б) кронштейн; в) штепсель; г) піксель.

10. На уроці фізкультури учні стали на відстані 1м один від одного. Весь ряд склав 25м. Скільки було учнів?

а) 24; б) 25; в) 26; г) 27.

1-й ведучий. (збирає бланки відповідей і віддає їх журі) Шановне журі, оцініть, будь- ласка, наших гравців. А ми, поки є час послухаємо Казку – головоломку «Сімнадцять верблюдів».

Це було давно. Жив в аулі старий Мокша. Було у нього троє синів. Коли Мокша помер, він залишив спадщину — 17 верблюдів і заповів розділити їх так: старшому сину віддати половину стада, середньому — одну третину, а молодшому —одну дев'яту частину стада. Причому умову висунув таку: жодного верблюда не різати.

Поховали діти батька і почали ділити спадщину. Ділили, ділили, але розділити не змогли. Старший вимагає собі половину стада — І7 навпіл, тобто 8,5; як же верблюда навпіл розділити? Середній син вимагає свою частину; одну третину від 17 — 5,75 верблюда; знову не виходить! Та й молодший не хоче поступатись; вимагає дев'яту частку стада - 1,88 верблюда.

Довго сперечалися брати, а вирішити нічого не змогли. У цей час на верблюді по аулу проїжджав старий чоловік. Під'їхав до братів та й питає:

— Про що ви сперечаєтесь, діти? Йому роз¬повіли. Посміхнувся лукаво старий і говорить:

— Я поділю!

І поділив спадщину. Усі троє братів залишились задоволеними, а старий сів на свого верблюда і поїхав далі.

Як мудрий старець розділив верблюдів?

Відповідь. Старий додав до 17 верблюдів свого. Потім стадо у І8 верблюдів він розділив на 2 частини і 9 верблюдів віддав старшому сину. Потім 18 розділив на З і 6 верблюдів віддав середньому сину. І нарешті 18 поділив на 9, 2 верблюди дістались меншому сину. Таким чином він дуже мудро розділив 17 верблюдів між синами (9+6 + 2 =17). А на своєму верблюді поїхав додому.

2-й ведучий. Слово для оголошення результатів першого туру надається журі.

ІІ тур. «Своя гра»

Умови конкурсу:

На ігровому полі розміщені назви 6 тем: інформатика, географія, арифметика, фізика, алгебра, жартівлива математика, геометрія, космонавтика. Ви за бажанням обираєте одну найцікавішу для вас тему і повинні будете відповісти на 7 запитань. Першим починає той, хто набрав більшу кількість балів в конкурсі «Розминка».

Поле для конкурсу «Своя гра»

	Арифметика	Жартівлива математика
Інформатика	Фізика	Геометрія
Географія	Алгебра	Космонавтика

Запитання до теми «Арифметика»

1. Як називається сота частина числа? (1%)

2. На яке число не можна ділити? (на 0)

3. Назвіть найменше семицифрове число. (1000000)

4. Скільки буде, якщо два десятки помножити на два десятки? (400)

5. Який знак треба поставити між числами 8 і 9, щоб одержати число більше за 8 і менше за 9? (кому)

6. Як називаються числа, які діляться на 2? (парні)

7. Яку частину години становить 20 хв? (третю)

Запитання до теми «Жартівлива математика»

1. Одне яйце вариться 5 хвилин. Скільки часу потрібно, щоб зварити шість яєць? (5 хвилин)

2. На дереві сиділо шість горобців. Вистріливши, стрілець поцілив двох. Скільки горобців залишилося на дереві? (жодного)

3. У батька 5 дочок і кожна має брата. Скільки дітей у батька? (шість)

4. На двох руках 10 пальців. Скільки пальців на 10 руках? (50 пальців)

5. На столі стояло три банки зі сливами. Петро з`їв одну банку слив. Скільки банок залишилось? (три, Петро банку не їв)

6. В кімнаті горіло три свічі. Одна погасла. Скільки свічок залишилось? (одна, дві інші згоріли)

7. На одній вербі було 25 груш, на іншій 15. Скільки всього груш зібрали діти? (жодної, на вербах груші не ростуть)

Запитання до теми «Інформатика»

1. Найстародавніший обчислювальний прилад (пальці)

2. Прилад, що відображає роботу на ПК (монітор)

3. «Світова павутина» (Інтернет)

4. Міні-комп`ютер для обчислень (калькулятор)

5. Пристрій для передачі інформації від людини до персонального комп`ютера (клавіатура)

6. Комп`ютерна програма, здатна до само розмноження , яка заважає ПК нормально функціонувати (комп`ютерний вірус)

7. Навчився програмуванню в 13 років. В 33 роки займав 131 місце в списку найбагатших людей світу. На даний момент його фірма займає перше місце серед виробників програмного забезпечення. (Білл Гейтс)

Запитання до теми «Фізика»

7 клас

1. Скільки кілограмів містить одна тонна? (1000кг)

2. Найменша неподільна частинка речовини (атом)

3. Як називається явище взаємного проникнення молекул чаю в проміжки між молекулами гарячої води? (дифузія)

4. Не стукне, не брякне, а у вікно ввійде. (світло)

5. Назвіть прилад для вимірювання серед знаків Зодіаку. (Терези)

6. В якому стані знаходиться джин, який, то вилазячи із пляшки, то залазячи назад, увесь час змінює свою форму і об`єм? (у газоподібному)

7. Ти за нею, а вона від тебе, ти від неї – вона за тобою. Що це? (тінь)

8 клас

1. Тепла гармошка весь дім обігріває. Що це таке? (парове опалення)

2. Вийшовши з води, собака струшується. Яке фізичне явище допомагає їй звільнитися від води? (інерція)

3. Яка тварина орієнтується в середовищі за допомогою ультразвуку? (кажан, дельфін)

4. Як можна підвищити температуру тіла, не нагріваючи його? (виконати над ним роботу: вдарити або натерти)

5. Як називається явище перетворення рідини в пару? (випаровування)

6. У чому тепліше: у трьох сорочках або в сорочці потрійної товщини? (у трьох сорочках)

7. Чому не можна гасити палаючу нафту водою? (густина нафти менша, ніж густина води, нафта підніметься над шаром води і продовжить палати)

9 клас

1. Вийшовши з води, собака струшується. Яке фізичне явище допомагає їй звільнитися від води? (інерція)

2. Плід цього дерева – один з найпоширеніших на Землі. Він, як розповідають легенди, став причиною однієї з найбільших війн стародавнього світу. Але він, за легендою, став причиною одного з найбільших фізичних відкриттів. Назвіть це дерево. (яблуня)

3. Як називається лінія, яку описує тіло при своєму русі? (траєкторія)

4. Яка сила зупиняє автомобіль, коли вимикають двигун? (сила тертя)

5. Яка фізична величина вимірюється в ватах? (потужність)

6. Прізвище видатного англійського вченого, що вивчав механічний рух і механічні закони природи. Його ім’ям названа одна з фізичних величин. (Ісаак Ньютон)

7. Фізична величина, що дорівнює добутку маси тіла на 9,8 Н\кг?(сила)

Запитання до теми «Геометрія»

7 клас

1. Чому дорівнює периметр трикутника зі сторонами 9см, 10см і 11см? (30см)

2. Як називається твердження, що потребує доведення? (терема)

3. Як називається прилад для вимірювання кутів?(транспортир)

4. Гострий кут він переріс, до тупого не доріс. Як називається такий кут? (прямий)

5. Дві прямі, що не перетинаються на площині.

6. Яким приладом вимірюється довжина відрізка?

7. Чому дорівнює сума суміжних кутів?

8 клас

1. Як називається прямокутник з рівними сторонами? (квадрат)

2. Як називається відношення протилежного катета до гіпотенузи? (синус)

3. Один з кутів паралелограма 80º. Чому дорівнює кут паралелограма, не рівний даному? (100º)

4. Теорема названа на честь математика і стосується прямокутного трикутника. (Теорема Піфагора)

5. Назва цього чотирикутника в перекладі з грецької звучить як обідній стіл. Форму цієї фігури мають вітрила на невеликому судні під назвою трабоколо. (трапеція)

6. Її дуже полюбляють льотчики, у географії позначають числами, про одну з них, яку захищали наші воїни під час Великої Вітчизняної війни, складено пісню. А в геометрії – це одна з відомих ліній у трикутнику та в інших многокутниках. (висота)

7. Усі знають, що два в квадраті це чотири, три у квадраті – дев`ять. А чому дорівнює кут у квадраті? (90º)

9 клас

1. Чому дорівнює площа квадрата зі стороною 5см? (25см2)

2. Як називається відрізок, що сполучає вершину трикутника із серединою протилежної сторони? (медіана)

3. Як називається відношення протилежного катета до гіпотенузи? (синус)

4. Як називається відрізок, який має напрям? (вектор)

5. Де розташований центр описаного навколо прямокутного трикутника кола? (на середині гіпотенузи)

6. Вчений, який знайшов, чому дорівнює квадрат гіпотенузи. Він брав участь у кулачному бою і виграв його, ставши олімпійським чемпіоном 58 Олімпіади, яка проходила в 548 році до н.е. (Піфагор)

7. Цим словом називають цупку бавовняну або шерстяну тканину з чіткими похилими рубчиками, а в геометрії – відрізок, який сполучає дві несуміжні вершини многокутника.(діагональ)

Запитання до теми «Географія»

1. Яку країну носять на голові? (Панама)

2. Найповноводніша річка України (Дунай)

3. Де на земній кулі протягом року день дорівнює ночі? (на екваторі)

4. Назвіть найкоротший день року (22 грудня)

5. Я хоч і маленький, та удаленький, Варто глянути на мене – і відразу знатимеш свій шлях. (компас)

6. Видно край, але скільки ні йдеш до нього, не дійдеш. Що це? (горизонт)

7. Де знаходиться північний магнітний полюс Землі? (біля південного географічного полюса)

Запитання до теми «Алгебра»

7 клас

1. Як називається рівність, що містить невідому величину? (рівняння)

2. Як називається сума одночленів? (многочлен)

3. Чому дорівнює Х*Х?

4. Як називається третій степінь числа? (куб)

5. Запам`ятати всі їх майже неможливо. За ними обчислюють значення виразу. Їх багато в довіднику. (формули)

6. Яке є найбільше трицифрове число?

7. Цифровий знак для позначення відсутності.

8 клас

1. Чому дорівнює корінь квадратний із 169? (13)

2. Скажіть формулу дискримінанта квадратного рівняння (Д = в2 – 4ас)

3. Про яку функцію іде мова в українській народній приказці «Хто багато погрожує, той мало шкодить»? (обернена пропорційність)

4. Що означає «скоротити дріб»? (розділити чисельник і знаменник на одне й те саме число, відмінне від нуля)

5. Обчисліть 34 (81)

6. Чому дорівнює число П? (3,14)

7. Як інакше називається незалежна змінна? (аргумент)

9 клас

1. Яка лінія є графіком квадратичної функції? (парабола)

2. Про яку властивість функції каже народна мудрість «Чим далі в ліс, тим більше дров»? (зростання)

3. Сформулюйте властивість, що допомагає розв`язати наступну нерівність: -3х > 6? (обидві частини правильної нерівності можна розділити на від`ємне число, знак нерівності при цьому змінюється на протилежний)

4. Як отримати графік функції у = 4|х| +3 із графіка функціїу =|х| ?

5. Числа записані в ряд: 2, 5, 8, 11, … Продовжіть цей перелік. (14, 17, 20,…)

6. Вказати нулі функції у=х(х-2) (0 і 2)

7. Як називається формула (а +b)2і чому вона дорівнює?

Запитання до теми «Космонавтика»

1. Які живі істоти першими побували в космосі? Це відбулося 3 листопада 1957р на борту першого космічного супутника. (собаки)

2. 20 липня 1969 року на кораблі «Аполлон-11» вперше людина висадилася на Місяць. Хто це був? (американський астронавт НейлАрмстронг)

3. Яка найближча до нас зоря? (Сонце)

4. Хто є основоположником теорії міжпланетних сполучень? (К.Е.Ціолковський)

5. Радянський конструктор першого космічного корабля з людиною на борту (С.П.Корольов)

6. Перший український космонавт, який у 1997 році у складі міжнародного екіпажу здійснив космічний політ на кораблі багаторазового використання «Колумбія» (Л.Каденюк)

7. 12 квітня 1961 р о 9год 07хв за московським часом відбувся перший в історії політ людини в космос. Корабель «Восток» с першим космонавтом Землі здійснив один виток навколо планети. Прізвище космонавта… (Ю.Гагарін).

Ведучий. Журі підраховує результати другого конкурсу, а в нас –математичні фокуси

а) "Скільки вам років?".

Ведучий звертається до присутніх: «Не хочете відповісти? Ну, добре, скажіть мені тільки, скільки буде, якщо від числа, в 10 раз більшого, ніж число ваших років, відняти добуток якого-небудь одноцифрового числа на 9».

Діставши відповідь ведучий говорить: «Дякую! Тепер я знаю, скільки вам років. Ви народились у...».

Відгадування. Від здобутого результату треба відокремити число одиниць і додати його до числа, що залишилося після відокремлення.

Нехай учневі 17 років і він виконав такі операції: 17 • 10 — 4х9 = 134. Почувши цей результат, ведучий додає числа 13 і 4 і дізнається, що учневі 17 років. Звичайно, після цього «відгадати» рік народження учня неважко.

б) "Живий арифмометр"

Учасникам конкурсу пропонується порахувати геометричні фігури.

Вважають так: 1-ий круг, 1-ий трикутник; 2-ий - круг; 1-ий квадрат і т.д. поки не зіб'ються. Переможцем оголошуємо того, хто більше порахує, поки не зіб'ється і хто швидше (використовується секундомір) .

ІІІ тур. «Поміркуємо логічно»

Умови конкурсу:

гравцям буде запропоновано 2 запитання з логічним навантаженням. Отримує бал той, хто правильно за відведений час виконає завдання.

Практичне завдання. За 1 хвилину ви повинні перекласти одного сірника так, щоб рівність стала правильною. Завдання оцінюється в 1 бал.

V – V = V

Відповідь: X – V = V

Магічний квадрат. За 1хвилину вам необхідно розгадати числовий ребус. В порожні клітинки магічного квадрату допишіть числа так, щоб сума чисел по всіх горизонтальних, вертикальних рядках і по двох діагоналях дорівнювалась 15. Завдання оцінюється в 2 бали.

	9	4
		3
6

1-й ведучий. А поки наші гравці працюють над завданням, ми проведемо вікторину для вболівальників.

Вікторина для вболівальників

1. Учитель математики Чарльз Лютвідж Доджсон став відомим завдяки своїм книжкам «Аліса в країні чудес», «Аліса в задзеркаллі». Який псевдонім автора? (Льюіс Керрол)

2. Один баварський комерсант поставив біля входу у свій магазин ваги, на яких кожен, хто входив та виходив, повинен був зважуватися. Для чого? (Щоб не змогли пронести вкрадене)

3. Відомий радянський фізик Ландау на вступних іспитах ставив запитання: продовжте ряд букв: О, Д, Т, Ч, …Як потрібно його продовжити? (П, Ш, С, … один, два, три, чотири, п`ять, шість, сім, …)

4. В одній сім`ї два батьки і два сини. Скільки всього людей в сім`ї? (три: дід, батько, син)

5. В якому числі стільки ж цифр, скільки й букв? (100)

6. У семі братів по одній сестричці. Скільки всіх сестер? (одна)

7. Яке число має таку ж кількість літер при написанні, скільки означає? (три)

8. Згадайте назви старих одиниць вимірювання довжини (долоня, п’ядь, лікоть, аршин, верста, дюйм, саджень, фут, миля)

9. У п’яти палок 10 кінців. скільки кінців у п’яти з половиною палок? (12 кінців)

10. Книга коштує гривню й ще півкниги. Скільки коштує книга? (2 гривні)

11. Назвіть народні прислів’я й приказки, в яких використовуються числа.

1. Не май сто карбованців, а май сто друзів.

2. При семі няньках дитя без догляду.

3. Заблукав поміж трьох сосен. (та інші)

2-й ведучий. Всім гравцям - прошу здати роботи для оцінювання їх в журі.

Поки журі виносить свій вердикт по третьому туру марафону, ми трохи відпочинемо. Гра називається «Ой, не можу!»

Гра «Ой, не можу!»

Для перемоги в цій грі треба бути уважними. Запрошую взяти участь у грі 6 гостей. Учасники гри повинні по черзі називати числа натурального ряду за винятком тих, які або діляться на 3, або містять цифру 3. Замість цих чисел треба говорити «Ой, не можу!». Наприклад, 1, 2, ой не можу, 4, 5, ой не можу, ...

Хто порушує правила гри, той вибуває і йде на місце. Так триватиме доти, поки не залишиться один учасник. Він і буде переможцем.

1-й ведучий. Слово для оголошення результатів третього туру надається журі.

ІV тур. «Це моя точка зору»

Ми зустрічаємось з науками щодня. Але чи дійсно вони нам потрібні?

Відеозапис «Чому потрібно вивчати математику?»

Чи потрібні знання взагалі людині? На це запитання ми просимо відповісти наших конкурсантів. Оцінюється грамотність, лаконічність, доказовість виступу. На підготовку дається 2 хвилини. Виступ оцінюється максимально в 5 балів.

(методичний прийом «Мікрофон»)

"Математичні танці".

1. Учні, які вміють танцювати, одержують паперові картки. На одних картках задачі, а на інших — відповіді на них. Той, хто розв'язав задачу, танцює з тим, у кого картка з відповіддю на цю задачу. Задачі розв'язують усно. У танцях бере участь стільки пар, скільки дано задач; тривають вони 5—10 хв. Хто перший знайде пару, той переможець.

Відеозапис «Падає сніжок…»

Прислів’я та приказки:

1. Ану вставай, чоловіче, третій півень кукуріче.

2. Артіль міцна, як всі за одного, а один — за всіх.

3. За одного вченого дають десять невчених.

4.Сім роківмак не родив і голоду не було.

5. Біда біду перебуде — одна мине, десять буде.

6. Сім мішків вовнита всі неповні.

V тур «Показуха»

Показати за допомогою жестів слова – математичні терміни.

1 Трикутник, його кути;

2 Пряма, точки А і B, що їй належать;

3 Квадрат, його діагоналі;

4 Кут, його бісектрису;

5 Промінь та йому доповняльний промінь;

6 Прямокутник, його кути.

За кожне правильно відгадане слово – 2 бали.

2-й ведучий. Журі підбиває результати конкурсів, а в нас – весела перерва…(виступи гумористів)

Хлопці розповідають гуморески Павла Глазового.

Мученик науки

Повернувся першокласник із занять додому.

Ніс в чорнилі, мов мазнули квачиком по ньому.

— Що з тобою, мій синочку? — засміялась мати. —

Та невже ти в школі носом учишся писати?

— Смійся, смійся, — каже хлопчик. — Зараз ти заплачеш,

Коли двійку у моєму зошиті побачиш.

Табель

Питається сина батько Опанас:

— Ну так де ж твій табель за дев'ятий клас?

— На деньок у мене попросив Марат.

— А чого це раптом?

— Каже, напрокат.

Учиться він класно, на "чотири" й "п'ять".

Хочемо їм табелем предків полякать.

Таткова доня

Сусід спитав мале дівчатко,

Чи самогонку варить татко.

Воно крутнуло головою:

— Не варить, ні!

Він п'є сирою.

Таємниця мозку

Кличе хлопець:

— Чуєш, татку!

— Чого тобі, синку?

— Я знайшов у себе в книжці цікаву картинку.

На картинці людський мозок. Череп ніби знятий…

Так чого в людини мозок геть увесь пом'ятий? —

Батько глянув, посміхнувся:

— Тут ясна картина.

Як народиться, синочку, на цей світ людина,

То вправляють і вправляютьїй «мозги» потрошку,

Доки стане в неї мозок схожим на гармошку

Найкраща мова

Йде синок до школи вперше.

Пита батька мати:

— Якій мові ми синочка

Будемо навчати —

Українській чи англійській?

Обидві ж хороші.

— Хай вивчає ту, якою

Печатають гроші.

1-й ведучий. Слово для оголошення результатів цього туру і гри в цілому надається журі ...

(Виступ журі. Нагородження учасників і переможців)

Вчитель .Як підсумок нашого заходу- гумореска «Шлюбний контракт».

Діти! Ви молодці! Ви всі сьогодні виграли. Хтось виграв, перемігши страх перед сценою, хтось – перед товаришами, хтось – перед собою. Ви здобули чергову перемогу над собою. Це головне! Спасибі вам за свято науки, що ви нам подарували!

І на закінчення я хочу згадати письменника Л.Толстого, який вважав , що людина схожа з дробом, знаменник якого є те, що вона про себе думає сама, а чисельник те, що про неї думають інші. Я бажаю всім учасникам змагання , щоб чисельник у вашому житті завжди був більший від знаменника.

Дорогі колеги, любі учні! Щиро вітаю усіх з Новим роком!Нехай новий рік буде для Вас щедрим на успіхи і принесе смак нових перемог! Нехай завжди вас супроводжує щаслива зірка, Боже благословення, а поруч панують любов, злагода та добробут!

До нових зустрічей! Дякую.

Колядка «Старий рік минає »

Здоровенькі були, школярі!

Я чув, що у вас сьогодні свято.

Можна до вас у гості? (Учні: Так )

Дякую. Мене звати Петро.

Ось яка історія зі мною вийшла.

Я теж колись був такий малий, як ви, та вчився у школі…

І була у нашому класі дівчина Галя…

А якою красунею вона була!

Очі – карі, брови – ниточками, малинові губи, коса – до пояса.

Закохався я у неї до безтями.

Галя уважно слухала на уроках.

І я теж уважно … дивився на Галю.

Ледь дочекавшись закінчення школи,

Я запропонував Галі свою руку і серце.

Галя відповіла мені взаємністю.

Я ж бо був козаком, нівроку.

І, як дівчина сучасна, вона уклала шлюбний контракт.

НУ…, щоб всю домашню роботу поділити навпіл.

За шлюбним контрактом одну половину денної роботи

Я маю виконувати до обіду, а другу половину денної роботи

Я маю виконувати після обіду, а моя Галя – решту роботи.

Хлопці, як ви вважаєте, такі умови шлюбного контракту хороші? ( Так)

О!.. Ви, напевне, теж в мою Галю закохані.

Я теж так вважав… І, що ви думаєте?

Я тепер за тим контрактом перу, борщі варю, вареники ліплю,

По господарці пораюсь… І так цілий день, і кожного дня.

А Галя - відпочиває і до обіду, і після.

Правда, серце у неї добре. Сама фарбується, чепуриться,

А інколи і самостійно їсть, що не по контракту.

Галя:

Ось де він! Я тебе скрізь шукаю.

Петю, чого ти так розбазікався?

У тебе, що роботи немає? Швиденько додому.

Я ж бо спішу з дівчатами на свято.

Петро: (до Галі)

- Не нервуй, люба Галю, я вже біжу.

(До глядачів)

Дякую, що ви мене вислухали,

Але , даруйте, мушу вже бігти.

Бо у цьому клятому шлюбному контракті

Ще про якісь штрафи та відсотки пише.

Бо ж коли ми на уроках математики вчили відсотки –

Я дивився на свою Галю.

Моя вам порада.

Слухайте уважно на уроках, або ж шукайте адвоката, Незакоханого в мою Галю.

«КЕНГУРУ» – ЦЕ ОСОБЛИВИЙ СВІТ

Блез Паскаль колись сказав: «Предмет математики настільки серйозний, що неварто пропускати нагоди зробити його трохи цікавим.»

Це і робить Міжнародна асоціація «Кенгуру без кордонів», що працює під егідою Юнеско.

Нікого сьогодні не здивуєш, що діти і навіть дорослі дуже люблять змагатись. У більшості змагань є переможці і переможені. Математичний конкурс «Кенгуру» є одним з тих змагань, у якому немає переможених. Адже участь у ньому є вже перемогою, перемогою над собою, над байдужістю, перемога зацікавленості над її відсутністю. Це перемога бажань більше знати, вміти. Світ, що оточує, надає безліч можливостей дітям проявити себе, позмагатись, виділитись серед інших.

Конкурс «Кенгуру» можна вважати першим масовим заходом стосовно впровадження тестування у вітчизняну освіту. Він може бути використаним при розв’язанні проблеми вимірювання досягнень учнів з математики, які впершу чергу пов’язані не з обсягом знань і вмінь, а з їх якістю, і в багатьох школах його так і використовують.

За характером завдань конкурс «Кенгуру» дуже близький до завдань міжнародних моніторингових досліджень ( TIMSS PISA) математичної грамотності і рівнів її компетенції. І саме тому конкурс «Кенгуру» сприяє впровадженню у вітчизняну школу компетентнісного підходу у навчанні. Результати конкурсу можуть бути використані для оцінювання високого рівня компетентності.

Конкурси «Кенгуру» - це свято кмітливості, натхнення, зацікавленості і просто небайдужості.

На початку 80-х років XX століття Пітер Холлоран, професор математики з Сіднею, вирішив організувати новий тип гри-конкурсу для австралійських школярів: підбірку задач із варіантами відповідей, перевірку яких здійснює комп’ютер. Тисячі школярів могли взяти участь у грі одночасно. Успіх австралійського національного математичного конкурсу був надзвичайний.

Вперше конкурс-гру «Кенгуру» в нашій державі було проведено у 1997 році на базі кількох шкіл Старосамбірського району Львівської області та Львівського фізико-математичного ліцею при Львівському національному університеті імені Івана Франка, викладач якого Пенцак Євген Ярославович був першим координатором гри «Кенгуру» в Україні. Завдяки його зусиллям і викладачів кафедри математики ліцею та при підтримці вчителів-ентузіастів із різних областей України конкурс став бажаним гостем у багатьох українських школах, ліцеях, гімназіях. Тепер це наймасовіше математичне та інтелектуальне змагання серед школярів нашої держави. Майже півмільйона учасників зібрав і об’єднав конкурс за 10 років.

Конкурс “Кенгуру” має на меті не лише зацікавити дітей математикою,- це і спроба об’єднати навколо вирішення спільних проблем вчителів математики з різних областей України. Зустрічаючись на щорічних семінарах у Яремчі на Закарпатті, які теж проводить оргкомітет конкурсу, вчителі діляться досвідом, слухають цікаві лекції своїх колег. Саме тут кожного року обговорюються і шліфуються задачі для наступного конкурсу, авторами яких здебільшого є самі його учасники. Найцікавіші задачі оргкомітет конкурсу кожного року надсилає до Міжнародного організаційного комітету, на засіданні якого досвідчені математики, що представляють кожну країну – учасницю, формують пакет завдань для майбутнього змагання. І вже потім ці задачі повертаються у вигляді завдань конкурсу.

Всі учні, які беруть участь у конкурсі урочисто на лінійці останнього дзвінка кожного року отримують відповідні сертифікати: за відмінні, добрі успіхи і просто за участь. А на лінійці, присвяченій першому дзвінку отримують інформаційні вісники – книжечки та призи.

$C:\Users\ПК\Pictures\Фотоколаж 5_Moment.jpg$

Учасники «Кенгуру» 2021

ВИСНОВКИ

Компетентнісний підхід до освіти – це спроба звести у відповідність освіти і потреби ринку праці. Він не є чимось новим, штучно створеним, а гармонійно поєднує традиційний підхід викладання, головним завданням якого є формування сталих знань, вмінь та навичок і особистісно-орієнтовану форму навчання, метою якої є створення умов для розвитку та самореалізації кожного учня.

Формування компетентностей учнів зумовлене не тільки реалізацією відповідного оновленого змісту освіти, але й адекватних методів та технологій навчання.

Компетентісне навчання забезпечує засвоєння знань та умінь, володіючи якими випускник школи знаходить підґрунтя для свого подальшого життя. Тому завданням учителя є:

створення умов для розвитку та самореалізації учнів;
задоволення запитів та потреб школяра;
засвоєння практичних знань, умінь;
розвиток потреби поповнювати знання протягом усього життя;
виховання для життя в цивілізованому громадянському суспільстві. Для розв'язання цих завдань учитель має керуватися такими правилами,
незалежно від стажу роботи, категорії, технології, яку він використовує:
головним є не предмет, якому ви навчаєте, а особистість, яку ви формуєте;
не предмет формує особистість, а вчитель своєю діяльністю, пов'язаною з вивченням предмета;
на виховання активності не шкодуйте ні часу, ні зусиль;
сьогоднішній активний учень - завтрашній активний член суспільства;
ставте учнів у ситуації, котрі вимагають виявлення та пояснення розбіжностей між фактами, що спостерігаються, та наявним знаннями;
допомагайте учням оволодіти найпродуктивнішими методами
навчально-пізнавальної діяльності, навчайте їх вчитися;
привчайте учнів думати та діяти самостійно, грамотно висловлюватися рідною мовою; доречно та коректно вживати в мовленні математичну термінологію;
творче мислення розвивайте, розв’язуючи задачі, практичного змісту; будуйте і досліджуйте найпростіші математичні моделі реальних об'єктів, процесів і явищ. Навчайте інтерпретувати та оцінювати результати своєї роботи;
слід частіше показувати учням перспективи їх навчання;
у процесі навчання обов'язково враховуйте індивідуальні особливості кожного учня, об'єднуйте в диференційовані підгрупи учнів з однаковим рівнем;

Вчитель повинен пам'ятати ці правила, слідувати їм, керуватися ними буде дієвою умовою, яка здатна полегшити учителю досягнення провідної найважливішої мети - формування та розвитку особистості.

Стародавні римляни вважали, що корінь навчання гіркий. Але коли вчитель бере в союзники інтерес, коли учні «хворіють» жагою знань і потягом до активної розумової праці, корінь навчання змінює смак.

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

Державний стандарт базової і повної середньої освіти освітньої галузі «Математика» (2011).
Навчальна програма з математики для учнів 10-11 класів загальноосвітніх навчальних закладів // Математика в школах України — 2018. — № 1-2. — С. 3-53.
Оновлені навчальні програми для загальноосвітніх навчальних закладів: Математика. 5 - 9 класи. (Червень, 2017 рік).
Боренкова З. І. Прикладна спрямованість навчання на уроках ма- тематики // Математика в школах України. — 2008. — № 27. — С. 21- 23.
Бурда М. І. Збірник завдань для державної підсумкової атестації з математики. 9 клас / М. І. Бурда, О. П. Вашуленко, Н. С. Прокопенко. — Х. : Гімназія, 2010. — 256 с.
Мерзляк А. Г, Полонський В. Б., Якір М. С. Алгебра: підручн. для 9 кл. загальноосвіт. навч. закладів. — Х. : Гімназія, 2009. — 320 с. ил.
Кравченко Ю, Суртмач О., Сусол О., Швець Л. Математичні задачі з елементами українознавства // Математика. — 2014. — № 20. — С. 18- 21.
Панішева О. В. Виховні можливості персоніфікації математики // Математика в школах України. — 2008. — № 28. — С. 33-38.
Саєнко Л. Задачі з екологічним змістом // Математика. — 2013. — № 16. — С. 21-23.
Сосницька В. Добірка задач практичного змісту // Математика.— № 27-28. — С. 31-35.
Шахненко О. Ф. Інформаційні задачі // Математика в школах України. Позакласна робота. — 2012. — № 12. — С. 20-21.

docx

Завантажити

Зберегти на потім

Додав(-ла)

Padiak Maria

Пов’язані теми

Математика, 6 клас, Методичні рекомендації

Додано

22 січня 2023

Переглядів

1687

Оцінка розробки

Відгуки відсутні