Формування компетентностей через квадрат двочлена.

Проект

Назва проекту:  Квадратний виклик: Формування компетентностей через квадрат двочлена.

Учасники проекту:

• Учитель

Лукашевська Мар’яна Іванівна (Верхньоворітський ЗЗСО I-III ступенів імені Софії Малильо Нижньоворітської с/р)

• Учні 7 класу

Діяльність учителя на уроці: вступає в діалог з учнями про реальні життєві ситуації, де потрібне розрахування площі або оцінка вартості. Наприклад, викладання плитки перед будинком або реконструкція простору; пояснює тему уроку: квадрат двочлена і його застосування для обчислення площ; створює мотивацію, пояснюючи, що проект не тільки про математику, а й про вміння розв’язувати реальні задачі; контролює роботу груп, допомагає і дає підказки, якщо необхідно; заохочує учнів обговорювати свої рішення і приходити до спільного висновку; підбиває підсумки проекту, наголошує на тому, як важливо правильно застосовувати математичні формули для розв’язання реальних життєвих задач; організовує рефлексію, запитуючи учнів, що їм було легко або важко, як вони можуть використовувати ці знання у повсякденному житті; надає домашнє завдання — індивідуальні або групові завдання для продовження теми.

Діяльність учнів на уроці: активно обговорюють можливі практичні завдання, діляться своїми думками щодо використання знань математики в повсякденному житті;  працюють у командах, обчислюють площу майданчиків за допомогою формули квадрата двочлена; обговорюють, як використовувати формулу для практичних завдань, спільно шукають рішення; вчаться формулювати та аргументувати свої відповіді; презентують результати своєї роботи, пояснюють свої розрахунки та рішення; слухають інші групи, ставлять запитання та обговорюють різні варіанти рішень; висловлюють свої враження від уроку, діляться тим, що вони зрозуміли і що було для них складним; рефлексують, як цей досвід допоможе їм у подальшому навчанні та житті.

Модельна програма: Модельна навчальна програма"Алгебра.7-9 класи"для закладів загальної середньої освіти (автори: Бурда М.І.,Тарасенкова Н.А.,Васильєва Д.В.).

Підручник: Алгебра,7 клас. Автор: Бевз Г.П., Бевз В.Г., Васильєва Д.В.

Опис проекту

Мета: дослідити і висвітлити в проекті важливість практичного застосування знань з алгебри, а саме квадрат двочлена, побудови системи суджень, які сприяють аналізу інформації та ухвалення раціональних рішень; застосування набутих знань на практиці при розв’язуванні життєвих задач.  

 

 

Завдання

Задача 1. Подай у вигляді многочлена вираз (ст.92, № 489).

Задача 2. Треба покласти плитку на квадратний майданчик перед будинком. Відомо, що ,довжина кожної сторони майданчика збільшиться на 3 метри після розширення. Початкова довжина сторони майданчика — 7 метрів. Скільки квадратних метрів плитки потрібно закупити для нового майданчика?

Задача 3. Чи вистачить 26 000 грн для закупівлі тротуарної плитки, щоб викласти 100 м²  майданчика, якщо 1 м² плитки коштує 260 грн?

І. Компетентнісний потенціал

1.Вільне володіння державною мовою

Уміння:

•     чітко і зрозуміло формулювати думки, аргументувати, ставити запитання і розпізнавати проблеми, активно брати участь у дискусіях
•     формулювати висновки на основі інформації, поданої в різних формах
•     доречно та коректно вживати в мовленні математичну термінологію, будувати логічно послідовні висловлювання, вести критичний та конструктивний діалог

Ставлення:

•     визнання важливості чітких і лаконічних формулювань та повага до оточуючих та до державної мови

2. Математична компетентність

Уміння:

•               обирати, створювати і досліджувати найпростіші математичні моделі реальних об’єктів, процесів і явищ, інтерпретувати та оцінювати результати
•     застосувати математичні знання у реальних ситуаціях, аналізувати і критично мислити, оцінювати та перевіряти свої рішення

 Ставлення:

•     готовність шукати пояснення та оцінювання правильності аргументів

3.Підприємливість та фінансова грамотність

Уміння:

•     генерувати нові ідеї, аналізувати, ухвалювати оптимальні рішення, розв’язувати життєві задачі
•     відстоювати власну позицію, дискутувати
•     аналізувати економічну ситуацію, родинний бюджет, використовуючи математичні методи

Ставлення:

•     розуміння важливості математичних розрахунків та оцінювання ризиків

 

ІІ. Реалізація основних позицій діяльнісного підходу.

•     Активність і самостійна робота учнів:

Учні самостійно виконують завдання у підручнику № 489, потім роблять взаємоперевірку. Перед розв’язанням завдання учитель проводить актуалізацію опорних знань учнів за допомогою вправи «Дерево рішень».

•     Практична спрямованість:

Застосування математичних знань при розв’язуванні завдання 2 є реальною задачею, що наближена до життя учнів.

•     Кооперація:

при розв’язуванні завдання 3 учні обмінюються ідеями, спільно досягають результатів.

•     Різноманітність форм і методів  роботи:

використовуються метод бесіди, дискусія, робота з підручником, інструктаж, спостереження, розв’язування вправ,створення проблемної ситуації, колективне її обговорення, учні роблять правильні висновки і т.ін.

 

ІІІ. Опис завдань (всіх трьох) із зазначенням галузевих критеріїв

 

 

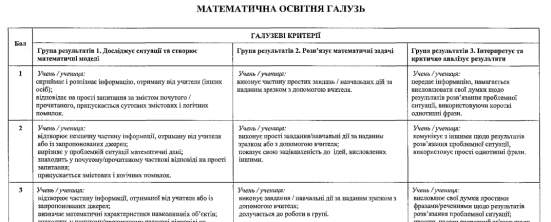
Опис і розв’язування завдань згідно нормативних документів

Приклад практичної задачі з реального життя, яка демонструє застосування формули квадрата двочлена для учнів 7 класу.

Задача 2: Треба покласти плитку на квадратний майданчик перед будинком. Відомо, що довжина кожної сторони майданчика збільшиться на 3 метри після розширення. Початкова довжина сторони майданчика — 7 метрів. Скільки квадратних метрів плитки потрібно закупити для нового майданчика?

Рішення:

1. Початкова довжина сторони майданчика: 7 метрів.
2. Збільшення сторони майданчика: на 3 метри.

Нова довжина сторони майданчика після збільшення: (7+3) метрів.

Відповідь:для покриття нового майданчика плиткою потрібно закупити 100 квадратних метрів плитки.

Ця задача не лише показує практичне застосування формули квадрата двочлена, але й допомагає учням зрозуміти, як математичні знання використовуються у повсякденному житті, зокрема при плануванні простору.

Для розв’язання задачі 2 за критеріями математичної освітньої галузі, учень має виконати ряд дій, які відповідають таким основним критеріям: досліджує ситуації та створює математичні моделі, розв’язує математичні задачі і критично аналізує результати. Розглянемо кожен із цих критеріїв у контексті задачі.

Критерій 1: Досліджує ситуації та створює математичні моделі

Учень повинен розуміти реальну ситуацію (укладання плитки на майданчик) і перетворити її на математичну задачу:

•                   Опис ситуації: Майданчик перед будинком має квадратну форму, і його розміри збільшуються на 3 метри з кожного боку після розширення. Початкова довжина сторони — 7 метрів.
•                   Створення математичної моделі: Модель базується на геометричних властивостях квадрата. Для визначення кількості плитки необхідно знайти площу нового майданчика, використовуючи формулу для площі квадрата S=a², де a — довжина сторони квадрата після розширення.
  •                   Початкова довжина сторони — 7 метрів.
  •                   Збільшення довжини сторони на 3 метри: нова сторона a=7+3=10a = 7 + 3 = 10a=7+3=10 метрів.
  •                   Модель для обчислення площі: S=10²=100 квадратних метрів.

Критерій 2: Розв’язує математичні задачі

На основі створеної математичної моделі, учень має виконати обчислення:

•                   Обчислення нової площі: Спочатку обчислюється площа нового майданчика після розширення: S=a²=10²=100 квадратних метрів.
•                   Це обчислення дає змогу отримати необхідну площу, яку потрібно покрити плиткою, тобто 100 квадратних метрів.

Критерій 3: Критично аналізує результати

Після виконання обчислень учень повинен оцінити правильність своїх результатів та їхню адекватність у контексті реальної ситуації:

•                   Перевірка результатів: Учень може перевірити, чи правильно застосована формула для площі квадрата. Переконується, що для розрахунку було взято нову довжину сторони (10 метрів) після розширення.
•                   Аналіз розширення: Критичний аналіз може полягати у порівнянні площі до та після розширення:
  •                   Початкова площа була S _{початкова}=7²=49 квадратних метрів.
  •                   Нова площа після розширення S_нова=10²=100 квадратних метрів.
  •                   Різниця площ: 100−49=51 квадратний метр. Це означає, що майданчик збільшився на 51 квадратний метр, що є логічним результатом з урахуванням розширення на 3 метри з кожного боку.

Підсумок:

•                   Результат: Учень вивів, що для покриття нового майданчика потрібно закупити 100 квадратних метрів плитки.
•                   Критичний аналіз: Учень критично оцінив, чи правильно проведені обчислення, перевірив коректність застосованих формул і зробив висновки на основі реальних змін площі після розширення.

Ці кроки демонструють, як за допомогою аналізу, математичного моделювання та критичного мислення можна ефективно вирішити задачу, що має практичне застосування.

Задача 3. Чи вистачить 26 000 грн для закупівлі тротуарної плитки, щоб викласти 100 м²  майданчика, якщо 1 м² плитки коштує 260 грн?

Розв'язок:

1. Знайдемо загальну вартість плитки для майданчика площею 100 м².

2. Чи вистачить 26 000 грн?

Вартість плитки для 100 м² майданчика становить 26 000 грн. Отже, якщо у вас є рівно 26 000 грн, то сума повністю покриває вартість плитки, але на додаткові витрати (наприклад, доставка чи підготовка майданчика) може не вистачити.

Тож 26 000 грн вистачить, але без запасу.

При розв'язуванні задачі 3, яка передбачає оцінку бюджету на закупівлю тротуарної плитки, учень використовує галузеві критерії математичної освітньої галузі: досліджує ситуації та створює математичні моделі, розв’язує математичні задачі та критично аналізує результати.

Критерій 1: Досліджує ситуації та створює математичні моделі

Учень повинен перетворити реальну ситуацію (планування закупівлі плитки) на математичну задачу:

• Опис ситуації: Необхідно визначити, чи вистачить 26 000 грн для закупівлі тротуарної плитки, якщо потрібно покрити 100 м² майданчика. Вартість 1 м² плитки становить 260 грн.
• Математична модель:
  •                       Кількість плитки, яку потрібно закупити: 100 м².
  •                       Вартість закупівлі обчислюється за формулою: Загальна вартість=площа×ціна за 1 м². Загальна вартість=площа×ціна за 1 м².

Модель виглядає так: Загальна вартість=100×260=26000 грн. Загальна вартість=100×260=26000 грн.

Критерій 2: Розв’язує математичні задачі

Після побудови моделі учень виконує обчислення:

• Розрахунок загальної вартості плитки: Загальна вартість=100×260=26000 грн. Загальна вартість=100×260=26000 грн.
• Це означає, що загальна вартість плитки для покриття 100 м² майданчика становить 26 000 грн.

Критерій 3: Критично аналізує результати

Після отримання результатів учень повинен оцінити, чи вистачить зазначеної суми для закупівлі плитки:

• Порівняння бюджету: Учень має бюджет 26 000 грн і бачить, що загальна вартість плитки також дорівнює 26 000 грн.
• Критичний аналіз:
  •                       Висновок: Сума в 26 000 грн рівно покриває вартість плитки для майданчика, тому учню вистачить цієї суми для закупівлі тротуарної плитки.
  •                       Учень також може врахувати можливі додаткові витрати (доставка, монтаж тощо), які не зазначені в задачі, але можуть бути критично важливими в реальному житті.

Підсумок:

• Результат: Сума у 26 000 грн вистачить для закупівлі плитки на площу 100 м² за умови, що вартість 1 м² становить 260 грн.
• Критичний аналіз: Учень розуміє, що даний бюджет покриває саме вартість плитки, але може знадобитися додатковий аналіз інших витрат.

Це завдання демонструє застосування навичок аналізу ситуації, побудови моделі та виконання критичного аналізу, що є ключовими в рамках математичної компетентності.

ІV. Сучасні ресурси

Назва, посилання, доцільність використання, результат

Приклад:

Назва і доцільність використання:

SketchUp – це програмне забезпечення для тривимірного моделювання. Учні можуть створювати 3D-моделі майданчика перед будинком, візуалізувати збільшення його розмірів,  зрозуміти просторові зміни та застосувати знання геометрії на практиці.

Посилання:

https://www.google.com/url?sa=i&url=https%3A%2F%2Fembed-3dwarehouse-classic.sketchup.com%2Fmodel%2Fa49b9fa3-b06f-4bbc-8a2a-aacbb2a269dc%2F%25D0%25B4%25D0%25B8%25D1%2582%25D1%258F%25D1%2587%25D0%25B8%25D0%25B9-%25D0%25BC%25D0%25B0%25D0%25B9%25D0%25B4%25D0%25B0%25D0%25BD%25D1%2587%25D0%25B8%25D0%25BA&psig=AOvVaw0xNphrR0_OdRdOQC18puQ8&ust=1729066483279000&source=images&cd=vfe&opi=89978449&ved=0CBQQjRxqFwoTCJDBweD4j4kDFQAAAAAdAAAAABAJ

Результат:

 

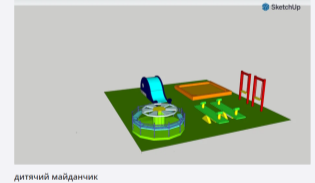
V. Висновки

1. В проекті досліджено і висвітлено важливість практичного застосування знань з алгебри, а саме квадрат двочлена, побудова системи суджень, які сприяють аналізу інформації та ухвалення раціональних рішень; застосування набутих знань на практиці при розв’язуванні життєвих задач.  

 

2.За допомогою сучасних  ресурсів, показано –як вони  допомагають не лише у вирішенні задачі, але й у формуванні математичних компетентностей, таких як створення моделей, аналіз результатів та використання математичних знань у житті.