Формування математичних компетенцій

НВК «Гімназія-школа» № 27

м. Маріуполь

Губська Олена Федорівна

Формування математичних компетенцій учнів

(додатковий матеріал до розробки уроку з геометрії)

Урок геометрії в 11 класі.

1. Розв’язання задач на обчислення об’єму тіла обертання. Учням пропонується зробити порівняльний аналіз методів розв’язання задач на обчислення об’єму тіла обертання, який надано в таблиці:

ПОРІВНЯЛЬНА ХАРАКТЕРИСТИКА ПЕРЕВАГ ДВОХ МЕТОДІВ ОБЧИСЛЕННЯ ОБ’ЄМУ ТІЛА ОБЕРТАННЯ

2. Проведення інтелектуального математичного турніру на уроці. Всіх учнів розбито на три групи, які повинні 15 хв. самостійно виконувати  описані нижче завдання і захищати свої роботи по 2 хвилини. Виступ опонентів по 1 хв., рецензента 1 хв. Кожний учень першої групи повинен розв’язати дві задачі, одна з яких надана з підказками. За це завдання можна отримати два бали. Після виконання завдання командою вибирається доповідач, який пояснює рішення двох задач. Друга група в цей момент грає роль опонента, критично ставиться до доповіді першої групи. Третя група грає роль рецензента. Умови задач для першої і другої груп:

 ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ

1 ГРУПА

1. Ромб обертається навколо прямої, яка проходить через вершину тупого кута ромба паралельно більшій діагоналі. Пряма лежить в площині ромба. Знайдіть об’єм утвореного тіла обертання, якщо діагоналі ромба дорівнюють 20 см і 10 см.  Відповідь:

2. Рівнобічну трапецію, основи якої дорівнюють 8 см і 18 см, обертають навколо більшої основи. Знайдіть площу поверхні тіла обертання, якщо відомо, що в цю трапецію можна вписати коло. Відповідь:

Інструкція:

• умова, коли в трапецію можна вписати коло;
• знайдіть висоту трапеції;
• проаналізувати, чи можна застосувати теорему Гульдіна;
• скористайтеся карткою розміщення центрів мас в многокутниках;
• знайдіть площу трапеції;
• обчисліть об’єм тіла обертання.

2 ГРУПА

1. Знайдіть площу осьового перерізу тіла, утвореного внаслідок обертання прямокутної трапеції, основи якої дорівнюють 4 см і 10 см, а більша бічна сторона - 10 см, навколо меншої бічної сторони. Відповідь:

2. Трикутник АВС обертається навколо сторони АС. Знайдіть об’єм тіла обертання цього трикутника навколо сторони АС, якщо АС=5 см, площа трикутника дорівнює 15 см. кв. Відповідь:

3. У частково заповнену водою циліндричну посудину, внутрішній діаметр якої дорівнює 8 см, повністю занурили металеву кульку радіуса 3 см. На скільки сантиметрів піднявся рівень води в посудині, якщо під час занурення вода з неї не виливалася? Відповідь: .

3. Завдання третьої групи. Кожний учень третьої групи повинен виконати творче завдання: скласти свої дві задачі на застосування теореми Гульдіна і розв’язати їх.

ОДНА З ЗАДАЧ КЕЙСУ,

СТВОРЕНИХ ТРЕТЬОЮ ГРУПОЮ УЧНІВ

Задача. Знайти об’єм тіла, яке утворюється при обертанні трикутника із сторонами 10 см, 14 см, 15 см навколо прямої, яка паралельна середній по довжині стороні, лежить в площині цього трикутника і знаходиться на відстані 7 см від цієї сторони.

Питання - підказки:

• Яке тіло буде утворюватися при обертанні?
• Чи можна застосувати теорему Гульдіна в цій задачі?
• Що необхідно знати, щоб обчислити відстань від середньої сторони до центра мас?
• Чи буде ця відстань дорівнювати значенню 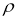в формулі?
• Де знаходиться в цьому трикутнику центр мас?
• Як полічити відстань від центру мас до прямої, навколо якої виконано обертання?
• Як можна обчислити площу заданого трикутника?
• Як обчислити висоту цього трикутника, яка проведена до середньої за довжиною сторони?
• Як обчислити ?
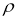• Чи можна знайти об’єм тіла обертання, у випадку згоди обчисліть цей об’єм?

Друга група учнів отримує від вчителя для самостійної роботи три задачі. За цю роботу учні можуть отримати три бали. Після виконання роботи групою обирається доповідач, який розповідає розв’язання цих задач. Третя група на цьому етапі грає роль опонента.

 7.3. Кожний учень третьої групи повинен виконати творче завдання: скласти свої дві задачі на застосування теореми Гульдіна і розв’язати їх. Це завдання для третьої групи оцінюється в чотири бали залежно від складності задачі. До кожної задачі необхідно створити інструкцію, яка допоможе іншим учням розв’язати ці задачі. Вони потрапляють до кейсу завдань, які будуть надані учням в наступних домашніх завданнях. Після виконання завдання групою обирається одна задача, яка буде зачитана під час захисту своєї роботи (додаток 11).