Урок "Піраміда. Бічна поверхня правильної піраміди"

Тема уроку:  Піраміда. Бічна поверхня правильної піраміди

Мета:

навчальна: сформувати поняття піраміди, познайомити учнів з елементами піраміди, видами пірамід, навчити визначати поверхню правильної піраміди;

розвиваюча: розвивати культуру математичної мови і пізнавальний інтерес, застосування в різних галузях знань;

виховна: виховувати інтерес до геометрії, працьовитість, прищеплювати бажання мати якісні і глибокі знання.

Обладнання: моделі піраміди, роздатковий матеріал, комп’ютер, мультимедіа.

Тип уроку:  урок засвоєння нових знань.

Хід  уроку

Математики навчає точності думки,

підкоренню логіці доведень,

поняттю строго обґрунтованої істини,

а все ж формує особистість, мабуть, більше, ніж музика.

                                                     О.Д. Александров

І. Організаційний етап.

ІІ. Мотивація навчальної діяльності.

Ми на попередніх уроках розпочали вивчення многогранників. Першим многогранником була призма і паралелепіпед. Сьогодні ми розпочинаємо вивчення іншого многогранника, який називається пірамідою.

 Піраміда – дуже цікава фігура не тільки з точки зору математики, а ще і як унікальний витвір всесвітньої культури.

Перше із семи див світу - ПІРАМІДА.

За давніх часів піраміди вважалися першими із семи див світу. І, виходячи з того, що нам відомо про інші шість чудес, можна сказати: для цього були всі підстави – піраміди і досі вважаються дивом із див! І хоч ми споруджаємо телевізійні вежі, куди вищі, а стадіони – куди більші, ніж найвища і найбільша із пірамід, - за компактно забудованою площею й масивністю її поки що не перевершила жодна новітня споруда.

 Виникає дуже багато запитань:

• Як могли стародавні єгиптяни визначити точну відстань від Землі до Сонця? (Адже висота найвищої піраміди в метрах, помножена на мільярд, дорівнює відстані від Землі до Сонця!)
• Чому бік основи цієї піраміди, поділений на подвоєну висоту дає число ?
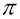• Чим пояснити, що, виходячи з розмірів найвищої піраміди, можна вирахувати дати всіх воєн та стихійних лих? Хто вклав в неї божественний план століть?
• Як пояснити той факт, що стародавні єгиптяни близько 4,5 тисяч років до нашої ери без компаса могли чітко зорієнтувати піраміди по частинах світу? (похибка становить менше 0,5⁰)

Переглянемо відео  https://www.youtube.com/watch?v=l19kQDYvmy0

За два століття досліджень на деякі з цих питань вчені вже мають відповіді або гіпотези. Що стосується математики, тут все означено і доведено.

III. Вивчення нового матеріалу.

Перший учень висвітлює такі питання:

     а) означення піраміди;

     б) елементи піраміди.

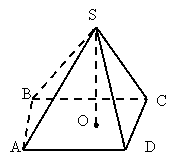
Пірамідою називається многогранник, який складається з плоского многокутника – основи піраміди, точки, яка не лежить у площині основи, - вершини піраміди і всіх відрізків, що сполучають вершину піраміди з точками основи

 

 

 

 

 

 

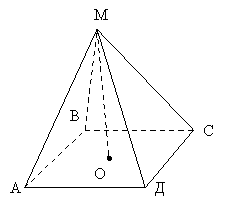
 АВСД – основа піраміди

 М - вершина

 МА, МВ, МС, МД – бічні ребра

 ▲МАВ, ▲МВС, ▲МСД, ▲ МАД – бічні грані.

 МО – висота.

 

 

 

 

 

 

Другий учень розповідає про види пірамід:

 

 а) Піраміди характеризуються за кількістю сторін в основі. Піраміда називається n – кутною, якщо її основою є n – кутник.

 

Трикутна піраміда називається також тетраедром:

 

 

                                                                                                                                                                                                                                                                                                                                                                                                                                                                           

 

 

 

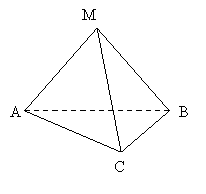
                                     Чотирикутна піраміда:

 

 

 

 

 

 

 

 

 

 

 

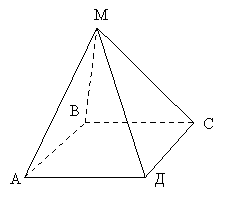
б) Піраміди бувають правильні і неправильні. Піраміда називається правильною, якщо її основою є правильний многокутник, а основа висоти збігається з центром цього многокутника.

 

 

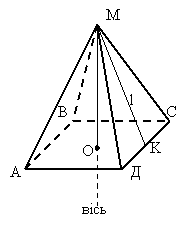
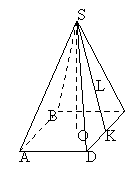
                                                   Правильна чотирикутна піраміда.

 пряма МО - вісь

 відрізок МО - висота

 L - Апофема

 АВСД – квадрат

 

 

 

 

 

 

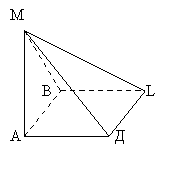
Неправильна чотирикутна піраміда

 

 

 

 

 

 

 

 

 

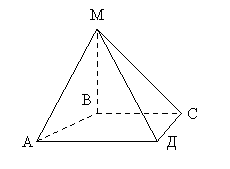
На дошці крейдою вчитель, а учні в зошитах будують правильну чотирикутну піраміду.

 

АЛГОРИТМ ПОБУДОВИ ПРАВИЛЬНОЇ ЧОТИРИКУТНОЇ ПІРАМІДИ

 

1. Будуємо паралелограм АBCD;
2. Знаходимо точку перетину діагоналей – точку О;
3. Проводимо висоту SO (S - вершина);
4. Сполучаємо вершину з точками основи;

 

 

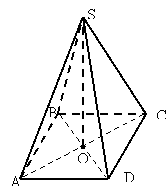правильно побудована піраміда                    неправильно побудована піраміда

 

 

 

 

 

 

 

 

 

 

Третій учень дає означення зрізаної піраміди і виводить формулу бічної поверхні піраміди.

 

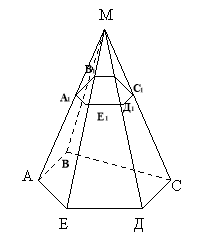
 АВСДЕ  ІІ А_1, В_1, С_1, Д_1, Е₁

 МАВСДЕ МА₁, В_1, С_1, Д₁

 АВСДЕ А_1, В_1, С_1, Д_1, Е_1.

 Зрізана піраміда:

                                                    2 основи, бічні грані трапеції.

 

 

 

 

 

 

Бічна поверхня піраміди – сума площ бічних граней.

 

Теорема 5.6.

Бічна поверхня правильної піраміди дорівнює добутку півпериметра основи на апофему.

 

                                                                                   Sбічн

   Довести, що Sбічн

                        

                  

 

                   На дошці крейдою:

 

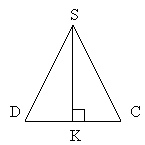
 S▲DSC=1/2 DC•SK

                                                 Sбічне = 4•S▲

 Sбічне =4•1/2•DC•SK=4•DC•1/2•P•L

 Sбічне=1/2•Ρ•L

 Sповне =Sоснови +Sбічне

 

 

 

 

Четвертий учень розповідає про застосування тіл пірамідальної форми в навколишньому середовищі. Тіла пірамідальної форми зустрічаються в будівництві, архітектурі. У вигляді шести- та восьмигранних пірамід (повних та зрізаних) будують каплички (невеликі церкви) та великі церковні храми. Дахами пірамідальної форми прикрашають кіоски, альтанки, «грибочки».

 У формі правильної чотирикутної піраміди роблять ковпаки над димоходами, щоб атмосферні опади не потрапляли в димохідну трубу.

 Музей сучасного мистецтва в Карасі (Венесуела) має  форму перевернутої піраміди.

 А в живописному березовому гаї Підмосков’я збудований комплекс молодіжного олімпійського табору. Його корпуси мають форму тригранних пірамід, дві бічні грані яких перпендикулярні до основи.

 Економний і практичний фундамент для будов сільськогосподарського призначення запропонували вчені інженерно-будівельного інституту. Він являє собою піраміду зі залізобетону, забиту в землю вершиною вниз. Така конструкція здатна добре переносити й вертикальні, й горизонтальні навантаження. При цьому не треба рити котлован, зводити фундамент. На таких «ногах» міцно стоять будинки й тваринницькі приміщення уже в багатьох областях.

 

П’ятий учень Одного разу до відомого математика А. М. Колмогорова звернулися будівельники однієї з гідроелектростанцій за порадою. Вони повідомили, що швидка течія річки не дає змоги перекрити її русло звичайним способом. Тому будівельники хотіли знати, якою повинна бути форма кам’яних брил, щоб зупинити швидку течію річки.

 Вчені зробили відповідні розрахунки і встановили, що річку потрібно перекрити бетонними тетраедрами. Крім того, вони підрахували, що таких тетраедрів повинно бути 7 500 штук.

  Щоб уникнути помилки, будівельники спочатку подвоїли цю цифру, а потім добавили ще. Приготували на березі 35 тисяч пірамід. Кинули в річку 7 500 штук, а решта залишилися лежати на березі річки як пам’ятник невірам у математику.

 У формі правильної піраміди роблять бункери для приготування розчину в будівельній справі. Таку ж форму мають і бункери зернозбиральних комбайнів.

 А французький інженер Фелікс Шамайко здійснив тристакілометрову подорож по Нілу на судні власної конструкції. Його «Анітрон» має чітку форму піраміди. За словами винахідника, вона вибрана не випадково. Він вважає, що піраміда – це символ спадковості в інженерній думці.

 Ажурну алюмінієву пірамідальну конструкцію утримують 32 пустотілі кулі і не дають судну перекидатися під час шторму.

 Багато пам’ятників споруджують у вигляді піраміди. Так, пам’ятник Вічної слави, який споруджено у київському парку на схилі Дніпра — це обеліск, верхня час­тина якого має форму правильної чотирикутної піраміди.

Не был наш путь к победе

ни легким, ни близким.

Тернистым, далеким и горестным

был.

И отмечен не только венцом

обелисков,

А тоской пирамидок и братских

могил.

(Ю.Югов «Символ слави»)

 

Шостий учень Я хочу нагада­ти про найдивніші споруди; що збереглися від стародавнього світу, — єгипетські піраміди. Се­ред них особливе місце посідає велика піраміда фараона Хеопса. Дослідники вважають, що в ній зашифровані знання тих часів з математики, астрономії тощо. Дивує точність інженерних розра­хунків стародавніх зодчих.

Блоки, з яких складена піраміда, так точно підібрані один до одно­го, що між ними не проходить навіть лезо ножа.

У цій піраміді має місце теорема Піфагора, золота пропорція та ін.

Послухайте вірш С. Острового «Пирамида»: _:

Стоит на земле пирамида,

и Боги о ней говорят.

На ней не рванье, не хламида,

а вечного камня наряд.

Она здесь стоять не устала,

хоть минуло много веков,

Она головою достала до самых

седых облаков.

Что людям она сохранила?

Великих камней забытье?

Зрачки желтоглазого Нила

лениво глядят на нее.

Кто спит в этой Древней могиле?

Расскажут ли камни о том,

Как всех их слезами солили

и кровью кропили потом.

Стоит на земле пирамида,

и Боги о ней говорят.

На ней не рванье, не хламида,

а вечного камня наряд.

Сьомий учень

 А я хочу роз­повісти про те, що відомий німе­цький поет Гете вважав піраміду таємничою містичною фігурою. Про це писав і біограф Гете — Іммерман. Але у своїх спогадах про Гете німецький письменник припустився однієї математичної помилки. Ось послухайте, що він пише: «Одного разу я відвідав Гете і застав його в. робочому кабінеті за цікавою роботою. Поет виготовив з картону трикут­ник і хотів на ньому продемонст­рувати співвідношення між ду­шевними силами людини. Чут­ливість він вважав основою серед усіх інших рис. Тому зобразив її в основі трикутника і зафарбував у зелений колір. Зафарбована в червоний колір бічна грань зоб­ражала фантазію, а в жовтий — здоровий глузд, у блакитний — розум. 

По-перше, трикутник не мав гра­ней, а мав сторони. По-друге, їх не чотири, а всього — три. Тож Іммерман припустився помилки. Гете, очевидно, виготовляв не трикутник. А що ж виготовляв поет? (Трикутну піраміду).

Восьмий учень розповість про застосування піраміди в медицині.

 Піраміда золотого перерізу Ю.Шінсе виготовлена із спеціального матеріалу і відтворює геометричні параметри давньоєгипетської піраміди Хеопса (до речі, за параметрами золотого перерізу побудовані також всі храми).

 Принцип золотого перерізу дозволяє концентрувати енергію геомагнітної піраміди, тонких енергоінформаційних потоків – їх частота набагато перевищує частоти, якими оперує сучасна фізика. До того ж золота піраміда дійсно покрита золотом  - молекули цього дорогоцінного металу вібрують на тій же частоті що і структури здорових клітин людського організму. Недарма на іконах німби у святих золоті, як і купола більшості соборів.

Згідно результатів клінічних досліджень, піраміда має стимулюючу дію на органи і системи пацієнтів, коректує їх функціональний стан.

Піраміда Ю. Шінсе лікує гіпертонію, хвороби серця, покращує формулу крові, виводить з депресивного стану, поліпшує стан хворих цукровим діабетом, зменшує болі в суглобах та м’язах.

Піраміда Ю.Шінсе не тільки покращує здоров’я дітей, але і позитивно впливає на їх психологічний стан, профілактику захворювань і здатність до навчання (показник відмінних робіт по Україні підсумкової атестації учнів складає 30 – 33%, а дітей, на яких діяла піраміда Ю.Шінсе 60 – 70 %).

Піраміда підвищує енергетичний потенціал, гармонізує відношення між членами родини, проблеми батьків-дітей.

       Виконання практичних завдань.

Сьогодні на уроці ми познайомились з новою фігурою – пірамідою.

Дізналися, які є види пірамід, як обчислити поверхню повної піраміди (формулу для поверхні зрізаної піраміди виведете самостійно).

Ви також послухали цікаву інформацію про застосування піраміди в практичній діяльності людини.

Тепер вашій увазі пропоную кілька задач і запитань.

1. «Мені потрібно склеїти з картону модель правильної піраміди, в основі якої лежить ромб з гострим кутом 60°, а  всі бічні ребра рівні між собою», - сказав Микола. «Такої піраміди не існує», - заперечив Іван. Чи правильне твердження Івана?
2. Які виміри треба зробити, щоб визначити висоту моделі правильної піраміди? Які треба зробити обчислення?
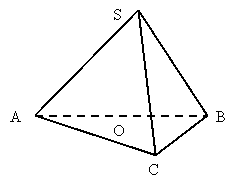3. Піраміда має рівні бічні ребра. В яку точку основи, що становить прямокутний трикутник, проектується вершина піраміди?
4. Дано правильну трикутну піраміду. Побудуйте кут:
   1. між бічним ребром і площиною основи;
   2. між бічною гранню і площиною основи;

 

 

 

 

 

Практична робота

1. На кожен стіл (двом учням) видається модель правильної піраміди. Потрібно зробити малюнок, відповідні виміри і обрахувати висоту піраміди. Завдання виконується в робочих зошитах.

V. Підведення підсумків уроку. Оцінювання учнів.

VІ. Домашнє завдання: О.В. Погорєлов «Геометрія 10-11»

 § 5 п. 27, 31, 32, 33, 34; №69