Завдання для підсумкових контрольних робіт з геометрії в 11кл.

Підсумкова контрольна робота

з геометрії

за І семестр

11 клас

І варіант

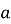
1. Основа піраміди – квадрат зі стороною . Висота піраміди дорівнює Н  і проходить через одну з вершин основи. Визначте площу бічної поверхні піраміди.

А) ;Б) ; В) ; Г) ;                  Д) .

2. Діагональ осьового перерізу циліндра дорівнює і утворює з    площиною основи кут  .  Знайти площу цього перерізу.

      А) ;  Б) ;  В) ;  Г) ;  Д) .

       3. Установити відповідність між сторонами основи та  діагоналями (1-4) бічних граней правильних трикутних призм та площами їх бічних поверхонь (А-Д).

                      1      3 см,  5 см                               А   

                      2      6 см,  10 см                             Б        

                      3       5 см,  13 см                            В    

                      4       7 см,  25 см                            Г    

                                                                               Д    

        4. Через дві твірні конуса, кут між якими дорівнює , проведено переріз. Знайдіть площу цього перерізу, якщо висота конуса дорівнює і утворює з його твірною кут .

         5. Діагональ основи правильної чотирикутної піраміди дорівнює , а бічна грань утворює з площиною основи кут . Знайдіть площу бічної поверхні піраміди.

Підсумкова контрольна робота

з геометрії

за І семестр

11 клас

ІІ варіант

          1. Знайти площу повної поверхні правильної чотирикутної призми, сторона основи якої дорівнює , а висота – .

А) ;    Б) ;    В) ;   Г) ;    Д) .

           2.  Радіуси основ зрізаного конуса дорівнюють 7 см і 15 см, а його твірна – 10 см. Знайти висоту конуса.

А) ;   Б) ;   В)  ;   Г) ;   Д) .

            3. Площа діагонального перерізу правильної чотирикутної піраміди дорівнює і є прямокутним трикутником. Установити відповідність між площею перерізу (1-4) та площею бічної поверхні (А-Д) піраміди.

                      1                                     А   

                      2                                     Б        

                      3                                В    

                      4                                   Г     

                                                                      Д    

                4. Паралельно осі циліндра проведено площину, яка відтинає від кола основи дугу . Діагональ утвореного перерізу нахилена до основи під кутом . Визначте площу перерізу, якщо радіус циліндра дорівнює .

                 5.  У правильній трикутній піраміді бічне ребро утворює з площиною основи кут 60°, а радіус кола, описаного навколо основи, дорівнює . Знайти площу бічної поверхні піраміди.

Підсумкова (річна)

 контрольна робота

з геометрії

11 клас

І варіант

1. Бічна поверхня циліндра в три рази більша за площу основи. Знайти відношення висоти циліндра до радіуса основи.

     А) ;    Б);    В) ;   Г) ;    Д) .

2. Діагональ куба дорівнює  . Знайти площу його повної поверхні.

           А) ;  Б) ;  В) ;  Г) ;  Д).

       3. Установити відповідність між геометричними тілами (1-4) та формулами для відшукання їх  поверхонь (А-Д).

                      1      Циліндр                                                      А   

                      2      Куля                                                            Б        

                      3       Конус                                                         В         

                      4       Правильна чотирикутна піраміда           Г    

                                                                                                  Д    

        4. У конусі через його вершину під кутом до площини основи проведено площину, яка відтинає від кола основи дугу . Радіус основи конуса R . Знайдіть об'єм конуса.

         5. У конус, площа бічної поверхні якого дорівнює і кут нахилу твірної до площини основи дорівнює , вписано трикутну піраміду. Основою піраміди є прямокутний трикутник з гострим кутом . Знайдіть об'єм піраміди.

Підсумкова  (річна)

 контрольна робота

з геометрії

11 клас

ІІ варіант

       1. Сфера дотикається до всіх граней куба. Знайдіть відношення площ їх  поверхонь.

                  А) ;    Б) ;    В) ;   Г) ;    Д) .

          2.  Знайдіть площу повної поверхні рівностороннього конуса, якщо його висота .

                 А) ;   Б) ;   В)  ;   Г) ;   Д) .

            3. Установити відповідність між геометричними тілами (1-4) та формулами для відшукання їх об'ємів (А-Д) .

                      1       Циліндр                             А   

                      2       Куля                                   Б    

                      3       Конус                                 В         

                      4      Піраміда                              Г     

                                                                           Д    

                4. Основою прямої призми є рівнобедрений трикутник з кутом β при вершині. Діагональ грані, яка проходить через бічну сторону основи, дорівнює і нахилена до основи під кутом α. Знайти об'єм призми.

                 5.  У  трикутну піраміду,  основою якої є прямокутний трикутник з гострим кутом , вписано конус. Знайдіть об'єм піраміди, якщо радіус основи конуса    а твірна нахилена до площини основи під кутом .