Формування пізнавального інтересу учнів на уроках математики

                                                  Левченко І. О.

вчитель математики

Краснопільської ЗОШ І-ІІІ ступенів

 

Формування пізнавального інтересу учнів на уроках математики

 

Питання активізації пізнавальної діяльності учнів є однією з найважливіших проблем сучасної освіти. Оскільки суспільство не може повноцінно функціонувати в умовах науково – технічного прогресу без активності людини. Пізнавальна активність особистості є умовою її духовного розвитку.

Фактором формування пізнавальної активності школярів є пізнавальний інтерес, формування якого займає важливе місце в комплексі виховних задач навчання математики. Він виступає не тільки чинником успішного навчання, а й є необхідною умовою розвитку особистості учня.

Відомий педагог Г. І. Щукіна в своєму визначенні пізнавальний інтерес розглядає як «вибіркову направленість особистості, що спрямована на область пізнання, на її предметну сторону і сам процес оволодіння знаннями» [4].

Пізнавальний інтерес належить до різних областей пізнавальної діяльності. Він може бути досить широким, розповсюдженим на отримання інформації взагалі, і поглибленим у певній області пізнання, в її теоретичні основи, зв’язки і закономірності.

У школі об’єктом пізнавальних інтересів учнів є зміст навчальних предметів. На пізнавальну активність школярів мають вплив усі компоненти методичної системи вчителя: цілі навчального процесу, форми, засоби, методи навчання (з урахуванням вікових особливостей учнів).

Створення у навчанні умов, які сприяють формуванню в учнів пізнавальних інтересів – це шлях, передумова підвищення якості навчання, якості всебічного розвитку особистості.

З метою аналізу причин, якими визначається ставлення учнів до математики, нами було проведено анкетування школярів Краснопільської ЗОШ І-ІІІ ступенів (смт. Краснопілля Сумської обл.). Загальна кількість опитаних – 318 учнів.

Дітям було запропоновано дати відповідь на таке питання:

     - Чи подобається вам математика ? Чому?

Для учнів старших класів до цього запитання додавалося ще два:

     - Що вам найбільш подобається вивчати на уроках математики?

     - Чи хотіли б ви обрати в майбутньому професію, пов’язану  з математикою?

Опитування учнів дали такі результати:

Таблиця 1

 

Класи	Кількість учнів, які позитивно відповіли на питання «Чи подобається вам математика» (%)		Кількість учнів, які негативно відповіли на питання «Чи подобається вам математика» (%)
5     6     7     8     9     10     11	96 %           71 %           61 %           56 %           53 %           44 %           31 %	4 %             19 %             39 %             44 %             47 %             56 %                     69 %
Всього по гімназії:	66 %	34%

 

Ми з’ясували причини, що зумовлюють позитивне та негативне ставлення учнів до математики. Більшість школярів, що позитивно ставляться до математики, вважають її цікавим предметом (36%). Подобається математика тим, кому вона легко дається (23%). Приблизно однакова кількість учнів, які вважають, що математика буде потрібна їм у майбутньому (18%), і тих, які своє захоплення математикою пояснюють тим, що вона розвиває логічне мислення (15%). На жаль, тільки 8% учнів вважають, що позитивне ставлення до математики зумовлено особистістю вчителя.

50% учнів, які негативно ставляться до математики, визнають, що вони її не розуміють (!).

Динаміку змін можна простежити за діаграмою

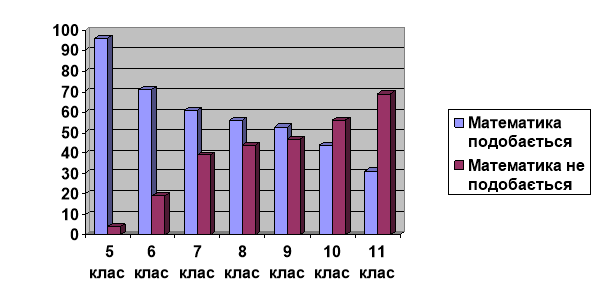        Відношення учнів середньої школи до математики змінюється в сторону негативу.

Одним зі шляхів розвитку пізнавального інтересу учнів до математики є використання інтегрованих уроків. Такі уроки не лише сприяють формуванню в дітей цілісного світогляду про навколишній світ; активізації їхньої пізнавальної діяльності; підвищенню якості засвоєння сприйнятого матеріалу, а й створюють творчу атмосферу в учнівському колективі, допомагають виявити у школярів здібності та їх особливості, розвивати пізнавальний інтерес до предмету, формувати навички самостійної роботи з додатковою літературою, таблицями, опорними схемами; поглиблюють розуміння учнями матеріалу, що вивчається.

Для сучасного етапу реформування української національної школи характерним є ускладнення змісту освіти, зростання обсягу необхідної інформації і зменшення часу, відведеного для її засвоєння. Сьогодні розвиток освіти як системи повинен реалізуватися через системні знання, що є необхідними для формування цілісного, системного мислення. Ці знання можуть бути отримані на основі інтеграції гуманітарних і фундаментальних дисциплін, а також повинні орієнтуватися на світовий рівень розвитку науки. Такий підхід сприяє відновленню цілісних уявлень про світ, картину світу як єдиного процесу [23].

Пошуки шляхів удосконалення системи освіти в школі спричинили до відродження такого методичного явища, як інтеграція навчання, що поступово переходить із дискусії в практику.

В Україні принцип інтеграції проголошений основним принципом реформування освіти поряд із принципами гуманізації та диференціації  [19]. За кордоном розробляється і впроваджується безліч освітніх технологій, що базуються на інтегрованих підходах.

Нині інтеграція набуває величезного значення у процесі освіти. Це відбувається у зв’язку із затвердженням Державного стандарту загальної середньої освіти: у школах вводять інтегровані курси, блоки, дні, уроки.

Майже традиційним у багатьох школах стало проведення інтегрованих уроків з математики та фізики, фізики та хімії, хімії та біології, української мови та математики, української літератури та музики.

Мета інтегрованих уроків – формування в учнів цілісного світогляду про навколишній світ; активізація їхньої пізнавальної діяльності; підвищення якості засвоєння сприйнятого матеріалу; створення творчої атмосфери в учнівському колективі; виявлення у школярів здібностей та їх особливостей; розвиток пізнавального інтересу до предмету; формування навичок самостійної роботи з додатковою літературою, таблицями, опорними схемами; поглиблення розуміння учнями матеріалу, що вивчається; ефективна реалізація розвивально-виховної функції навчання. Такі уроки ґрунтуються на міцних міжпредметних зв’язках, що дає можливість довести цілісність освіти, розвивати на новому якісному рівні творче мислення, інтелект та емоційні образні почуття школярів.

Успішне вивчення учнями одного предмета залежить від наявності у них певної бази знань і вмінь. Ізольоване викладання теми на базі одного предмета нерідко є шкідливим, недостатнім, адже ми все чіткіше розуміємо, що світ єдиний, він має багато внутрішніх зв’язків, у тому числі не можна торкатися жодного важливого питання, не поставивши при цьому багатьох інших. У подібних випадках необхідними є порівняння, зіставлення, а це також є основою для інтеграції. Під час детального вивчення програм із різних предметів, легко помітити, що є чимало «перехресних», подібних тем, загальних проблем і питань. Нерідко вивчаються одні й ті ж процеси та явища, розглядаються з різних позицій одні й ті ж об’єкти. Все це є «заявкою» на інтеграцію, хоча б за окремими темами [13].

Потребу у виникненні інтегрованих уроків можна пояснити наступними причинами:

1. Наявність інтегрованих процесів у всіх сферах людської діяльності.
2. Природна потреба школярів цілісно пізнавати навколишній світ.
3. Створення сприятливих умов для реалізації особистісно орієнтованого та розвивального навчання. «Система освіти має змінитися таким чином, щоб дитина стала тим сонцем, навколо якого обертаються всі освітні засоби, тим радіусом, який визначає розмір усього кола шкільного життя» [10].
4. Необхідність позбавлення перевантаження учнів.
5. Усунення дублювання навчального матеріалу.
6. Поглиблене всебічне вивчення конкретних предметів, фактів, явищ.
7. Скорочення кількості навчальних годин протягом тижня, вилучення їх для предметів розвивально-виховного циклу.
8. Впровадження результатів творчих пошуків учителів у практику. 

Інтегровані уроки є чудовим засобом підвищення зацікавленості учнів на уроках математики. Вони пробуджують у дітей палке прагнення до знань і до навчання. Варіанти інтегрованих уроків є різноманітними. Можна зінтегрувати математику з одним, двома, навіть трьома предметами на одному або декількох уроках. Але не потрібно забувати, що в основі інтегрованих уроків повинна бути близькість змісту основних тем різних предметів, їх гармонійне комплексне взаємопроникнення. Наприклад, у 7-му класі ми пропонуємо провести такі інтегровані уроки.

2.2.3. Інтегрований урок з математики та географії

Тема. Множення многочлена на многочлен.

Мета: сформувати вміння множити одночлен на многочлен і многочлен на многочлен; використати отримані теоретичні знання для розв’язання задач різних рівнів; сприяти вихованню всебічно розвинутої особистості, вихованню активної життєвої позиції; розвивати емоційну сферу учнів.

Тип уроку: урок комплексного застосування знань, умінь і навичок.

Обладнання: політична та фізична карти Африки, кольорові портрети представників різних рас Африки, дидактичний матеріал «Алгебра в таблицях, 7 – 9 класи», кольорова крейда.

Хід уроку

           І. Організація класу та оголошення теми і мети уроку.

Учитель математики. Діти, сьогодні в нас незвичайний урок математики. Ви вже знаєте, що математику можна поєднати з різними науками. Ми розв’язували з вами історичні задачі, задачі фізичного змісту, поєднували математику з українською літературою. А зараз проведемо цікавий урок математики та географії.

Учитель географії. На цьому занятті ми дізнаємося багато цікавого про населення Африки.

Учитель математики. Та будемо закріплювати вміння множити одночлен на многочлен і многочлен на многочлен.

ІІ. Перевірка домашнього завдання.

Учням можна запропонувати завдання, аналогічні до завдань із домашньої роботи. У розв’язанні кожного з прикладів навмисно існує помилка, яку потрібно знайти й виправити.

Завдання. Знайдіть помилку в розв’язанні й виправте її:

1) (х + 2)(х – 7) = х² + 5х – 14;

2) (х + 3у)(х – 4ху + 2у²) = 2х – 12ху² + 3у²х + 6у³;

3) (3 – 4х)(2х² - х – 1) = 6х² - 3х – 3;

4) 3аb(2а - аb) = 6аb - 3аb;

5) (4х – 3у + 1)(3у² + 3х²) – 3х²(4х – 3у²) = -9у + 3у² + 3х² + 24х³.

Правильний розв’язок:

1) х² - 5х – 14;

2) х² - 10у²х + 3ух – 4х²у + 6у³;

3) 10х² + х – 8х³ - 3;

4) 6аb - 3аb;

5) -9у + 12у²х + 3у² + 3х².

Учитель географії. А тепер давайте пригадаємо, на які основні раси поділяють населення Землі?

- Що таке густота населення?

- Які країни називають колоніями?

До речі, а ви знали, що Африка – прабатьківщина людини? У Східній Африці археологи знайшли рештки прадавньої людини і знаряддя її праці, вік яких близько 2,7 млн. років. Такого віку знахідки є найдавнішими на нашій планеті. Це дає підставу припустити, що перші люди на Землі були африканцями, що саме в Африці зародилося людство. Звідти давні люди почали розселятися по всьому світу.

ІІІ. Актуалізація опорних знань.

Учитель математики. Зараз виконаємо такі завдання:

1. Прокоментуйте, використовуючи алгоритм множення одночлена на многочлен, розв’язання прикладу 5ху(у – 8х).

2. Прокоментуйте, використовуючи алгоритм множення многочлена на многочлен, розв’язання прикладу (2а – 3)(а² - 5а + 3).

IV. Комплексне застосування знань.

Учитель географії. Африка характеризується надзвичайним різноманіттям рас, народів, племен. Серед її населення є представники і негроїдної, і європеоїдної, і монголоїдної рас.

Учитель математики. Зараз проведемо невеликий математично-географічний турнір.

Клас об’єднується в три команди – «представники негроїдної раси», «представники європеоїдної раси» та «монголоїди». Перед початком турніру представники команд (заздалегідь підготовлені учні) розповідають про «свою» расу. Ці розповіді доцільно супроводжувати показом фотографій на проекторі.

Перший учень. Більшу частину материка населяють представники негроїдної (екваторіальної) раси. В умовах палючого сонця їхня шкіра набула темного кольору, що захищає її від опіків, а волосся стало кучерявим. Народи і племена цієї раси мають значні відмінності у відтінках шкіри, зрості, рисах обличчя. В екваторіальних лісах живуть пігмеї (рис. 2.3). Це найменші люди нашої планети, їх середній зріст становить 145 см.

Рис. 2.3

Натомість масаї і тутсі ( рис. 2.4)– найвищі з народів Африки, їх зріст досягає 2 м.

Вони на диво стрункі та граційні.

Рис. 2.4

Нілоти (рис. 2.5) «люди Нілу», які живуть у верхів’ях цієї річки, також високого зросту. Крім того, вони вирізняються надзвичайно темним, майже чорним кольором шкіри.

Рис. 2.5

Суахілі (рис. 2.6) – «люди узбережжя» - населяють прибережні райони Індійського океану.

Рис. 2.6

Другий учень. На півдні материка живуть бушмени і готтентоти  (рис. 2.7).  Вони низькорослі, мають жовтувату зморшкувату шкіру, вилицювате обличчя, що робить їх схожими на монголоїдів.

Рис. 2.7

Ефіопи (рис. 2.8), які мають світліший, ніж у негроїдів, колір шкіри з червонуватим відтінком, походять від негроїдної та монголоїдної рас.

Рис. 2. 8

Третій учень. Представники європеоїдної раси живуть в основному на півночі Африки. Це араби (алжирці, єгиптяни, марокканці), які говорять арабською мовою, і бербери (рис. 2.9) . Вони мають світлий, проте досить смаглявий колір шкіри.

Рис. 2.9

 У багатьох районах Африки проживають європейці. Передусім на півдні, де оселилися нащадки голландських, англійських, німецьких, французьких переселенців. Там багато і мулатів (рис. 2.10), які походять від змішаних шлюбів європейців з місцевим населенням.

Рис. 2.10

Учитель математики. Кожна команда має розв’язати 2 завдання. За певний час (8 – 10 хвилин) кожний учень має записати в зошит розв’язання завдань, запропонованих команді, й пояснити хід розв’язування. Члени команди можуть консультуватися одне з одним. Потім починається турнір.

Учитель географії. Капітан команди І викликає для участі в турнірі представника команди ІІ. Капітан команди ІІ викликає представника команди ІІІ. І відповідно капітан команди ІІІ викликає учня з команди І.

Учитель математики. Пари учасників обмінюються завданнями, розв’язаними їхньою командою (на вибір). Учні йдуть до дошки й починають розв’язувати їх на дошці.

Учитель географії. Таким чином, кожна команда розв’язує не лише свої завдання, а й завдання команди-суперниці, щоб у разі потреби надати гравцеві своєї команди допомогу.

Учитель математики. Перемагає та команда, яка правильно розв’яже та пояснить більшу кількість завдань іншої команди. За відповідями й правильністю розв’язань стежать усі учні.

Завдання для І команди

1. Розв’язавши рівняння (х – 4)(х + 2) – (х - 5)(х – 6) = -10х та помноживши отриманий результат на загальну кількість учнів у класі (25), одержати число, яке дорівнює кількості країн в Африці.

2. Використовуючи лінійку та враховуючи масштаб карти, визначити наближено площу Нігерії.

Завдання для ІІ команди

1. Знайшовши значення виразу (х + 2)(х – 7) + 28 та підставивши замість х число 6, одержати число, яке показує середню густоту населення Африки (осіб/км²).

2. Використовуючи лінійку та враховуючи масштаб карти, визначити наближено площу Єгипту.

 Завдання для ІІІ команди

1. Знайшовши значення виразу (3 – 4х)(2х² - х – 1) + 153 + 7х³ та підставивши замість х число 4, обчислити кількість народностей, які проживають в найбільшій країні Африки за кількістю населення  - Нігерії.

2. Використовуючи лінійку та враховуючи масштаб карти, визначити наближено площу Ефіопії.

Відповіді до завдань математичного турніру

І команда. 1. 50 країн.

                   2. 924 тис. км².

         ІІ команда. 1. 20 осіб/км².

                   2. 1 млн. км².

 

        ІІІ команда. 1. 250 народностей.

                   2. 1,1 млн. км².

Учитель географії (після оголошення команди – переможниці турніру). А тепер давайте разом попрацюємо з політичною картою Африки (рис. 2.11).

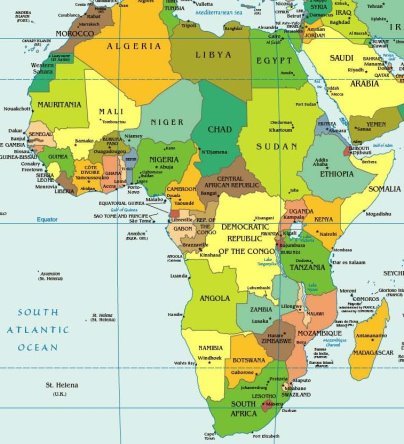
Рис. 2.11

В сучасній Африці понад 50 великих і малих держав. Ще 50 років тому майже всі країни цього материка були колоніями. Могутні держави Європи з часів відкриття Африки сприймали її як скарбницю, звідки можна було черпати спочатку золото, слонову кістку, цінну деревину, а потім – рабів і корисні копалини. Починаючи з XVI ст. вони поділили Африку між собою і збагачувалися за рахунок захоплених земель. Найбільше територій захопили Велика Британія і Франція.

Народи Африки тривалий час боролися проти колоніалізму. З 1960 р. в Африці з’явилися десятки незалежних держав, а в 1990 р. незалежною стала остання колонія Намібія.

Хоча зараз уже немає колоній, деякі з держав Африки і донині перебувають в економічній залежності від колишніх власників. За рівнем розвитку держави Африки належать до країн, що розвиваються. Високорозвинутою є тільки країна Південна Африка.

Завдання до класу:

1. Визначте найбільші за площею країни Африки. За допомогою лінійки, враховуючи масштаб карти, обчисліть наближено їх площі.

2. Використовуючи фізичну та політичну карти Африки, знайдіть країни, території яких лежать у зоні пустель.

3. Щороку Єгипет відвідують 2 млн. туристів. Кожний з них витрачає в країні щонайменше 500 доларів США. Обчисліть щорічні прибутки країни від туризму. Зробіть висновок про значення цієї галузі для економіки Єгипту.

V. Підбиття підсумків уроку.

1. Запитання до класу:

- Чим ми займалися на уроці?

- Чи сподобалась вам така форма уроку?

2. Оголошення оцінок.

VI. Домашнє завдання.

Повторити алгоритми множення одночлена на многочлен, многочлена на многочлен і розв’язати задачу.

Задача. Довжина прямокутника на 3 см більша за його ширину. Якщо довжину зменшити на 2 см, а ширину збільшити на 5 см, то площа прямокутника збільшиться на 14 см². Знайти початкові довжину й ширину прямокутника.

А також поміркувати, чому офіційними мовами в багатьох країнах Африки є французька або англійська.

 

Вивчивши можливості інтегрованого навчання, можна впевнено сказати, що за ним – велике майбутнє.

Змістовні та цілеспрямовані інтегровані уроки вносять у звичайну структуру шкільного навчання новизну та оригінальність; сприяють формуванню цілісної картини світу, розгляду об’єкта з кількох сторін; дозволяють систематизувати знання; створюють сприятливі умови для реалізації особистісно орієнтованого, розвивального навчання школярів.

Методично правильні побудова та проведення інтегрованих уроків сприяють зростанню професійної майстерності вчителя, тому що вимагають від педагога володіння методикою сучасних технологій навчально- виховного процесу. Вчитель по-новому бачить і розкриває предмет, який викладає, ясніше усвідомлюючи його співвідношення з іншими науками.

 

При бажанні таких задач та історичних відомостей можна відшукати багато. Їх підбірка залежить від ерудованості, бажання та смаку вчителя.

Отже, включення до уроку математики елементів історії допомагає показати учням, що математика – жива наука, яку створили і продовжують створювати люди. Це сприяє підвищенню інтересу школярів до вивчення математики, формування їх критичного мислення та наукового світогляду, що є одним з основних завдань сучасної школи.

Використана література:

1. Вивальнюк Л. М., Ігнатенко М. Я. Елементи історії математики: Навч. Посібник. – К.: ІЗМН, 1996.
2. Нагибин Ф. Ф., Канин Е. С. Математическая шкатулка. – М.: Просвещение, 1988.
3. Чистяков В. Д. Старинные задачи по элементарной математике. – Минск: Высш. шк.,1966.
4. Щукина Г. И. Активизация познавательной деятельности учащихся в учебном процессе. – М.: Педагогика, 1979.