Функції та їх властивості

Про матеріал

Методичні рекомендації учням до вивчення розділу «Функції, їх властивості і графіки» містять основні теоретичні відомості, приклади розв'язування задач, питання та завдання для самоконтролю знань а також список необхідної літератури.

Перегляд файлу

Функції,

їх властивості і графіки

Зміст

$D:\Мої документи\Світлана\Атестіція\2017\узагальнння досвіду\Вензель_7.png$

Числові функції. Способи задання функцій. – 2

Область визначення і множина значень функції. – 5

Неперервність функції. - 7

Обернена функція та її графік. – 10

Складна функція. – 12

Монотонність функції. – 13

Парність і непарність функції. – 15

Графіки основних елементарних функцій та їх властивості. – 19

Перетворення графіків функції. – 31

Список використаної літератури-38

$D:\Мої документи\Світлана\Атестіція\2017\узагальнння досвіду\Вензель_7.png$

Числові функції. Способи задання функцій.

Поняття функції:

Функція – це правило, за допомогою якого за кожним значенням незалежної змінної х з деякої множини Х можна знайти єдине значення залежної змінної у з множини Y.

Записують: y=f(x). Змінну величину х називають незалежною змінною, або аргументом, а у – залежною змінною, або функцією.

Способи задання функцій:

Табличний – має вигляд таблиці, в І-му рядку виписані всі значення аргументу, в ІІ-му рядку числа утворені за правилом y=f(x).

Приклад 1.

t^o, c	12	19	26	50
V, см³	1	1,03	1,14	1,19

Аналітичний – полягає в тому, що функцію задають за допомогою формули, яка дає можливість обчислити значення функції пр. довільному значенні аргументу, до якого вона визначена. Має вигляд рівності y=f(x).

Приклад 2.

Графічний – відповідність задається множиною точок координатної площини, координати х і у дорівнюють аргументам х і значенням функції у в цих аргументах. Графіком функції може бути деяка крива, зокрема пряма, множина окремих точок на площині тощо.

У техніці і фізиці часто користуються графічним способом задання функції при дослідженні реальних процесів. Існують прилади, які видають оброблену інформацію у вигляді графіків. Так, у медицині використовують електрокардіограф. Цей прилад показує криві, які характеризують роботу серця.

$C:\Users\User\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\barigo-digital-lcd-barograph-2050ma-165929-600x600.jpg$ $C:\Users\User\Documents\fx-7302.jpg$

Барограф Електрокардіограф

Приклад 3. Графічний спосіб задання функції:

4. Словесний – полягає в тому, що закон, за яким обчислюють у, описується словами.

Контрольні запитання:

Що таке функція?
Що називають аргументом функції?
Що називають значенням функції?
Які способи задання функції ви знаєте?

Вправи:

Функцію задано формулою

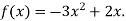
Знайдіть: .
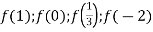Знайдіть значення аргументу, при якому значення функції дорівнює: 0; -1; -56.
Чи є правильною рівність: .

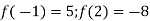Функцію задано формулою .

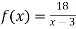Знайдіть: .
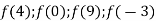Знайдіть значення x, при якому:

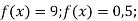
Функцію задано формулою 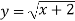. Заповніть таблицю відповідних значень х і у:

х	2		-1,75
у		5		0,4

Функцію задано формулою 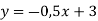. Заповніть таблицю відповідних значень х і у:

Х	-4		1,2
у		2		-5

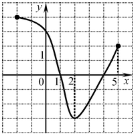На рисунку 1 зображено графік функції 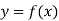. Користуючись графіком знайдіть:

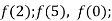
значення х, при яких

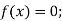
Рис. 1.

Область визначення і множина значень функції

Область визначення функції – множина тих значень, які може приймати аргумент.

Позначають D(f) або D(y).

Приклад 4. Знайти область визначення функції

Розв’язання. Розв’яжемо нерівність

Знайдемо корені відповідного рівняння: .

Відмітимо отримані розв’язки на координатній прямій і знайдемо знак виразу на кожному проміжку.

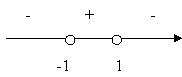
Відповідь: D(y)=(-1;1).

Множину значень, яких набуває залежна змінна у, тобто множину Y, називають множиною значень функції.

Позначають Е(f) або Е(y).

Приклад 5. Знайти множину значень функції

Розв’язання. Виділимо з квадратного тричлена повний квадрат:

Оскільки вираз набуває лише невід’ємних значень, то Е(y)=[4; +∞).

Коли D(f)і Е(y), функцію f називають числовою.

Функцію вважають заданою, якщо вказано її область визначення і правило, за яким за кожним значенням незалежної змінної з області визначення можна знайти значення залежної змінної з області значень.

Контрольні запитання:

Що називають областю визначення функції?
Що називають множиною значень функції?
Що треба вказати, щоб функція вважалася заданою?

Вправи:

Знайдіть область визначення функції:

Знайдіть множину значень функції:

Неперервність функції

Функція називається неперервною в точці х_о, якщо існує границя функції в цій точці і вона дорівнює значенню функції в точці х_о.

Отже, функція у = f(x) в точці х_о, буде неперервною тоді і тільки тоді, коли виконуються умови:

1) функція у = f(x) визначена в точці х_о, ;

2) для функції існує границя ;

3) границя функції f(x) в точці х_о, дорівнює значенню функції в цій точці: .

Якщо функція у=f(x) неперервна в кожній точці деякого проміжку, то її називають неперервною на даному проміжку. Справедливі такі теореми.

Теорема 1. Якщо функції у = f(x) і у = g(x) є неперервними в точці х , то в цій точці будуть неперервними й функції у = f(x) ± g(x) та у = f(x) – g(x).

Теорема 2. Якщо функції у = f(x) і у = g(x) є неперервними в точці х_о і , то в точці х_о, буде неперервною також і функція .

Приклад 6.

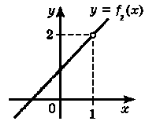
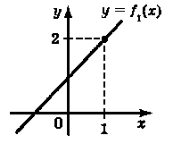
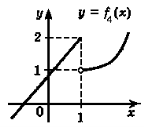
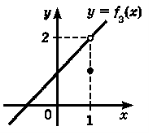
Рис. 2.

Розв’язання. На рис. 2 розривними функціями є функції f₂, f₃, f₄, які мають розрив в точці х = 1.

Контрольні запитання:

Яка функція називається неперервною в точці?
Сформулюйте теореми про неперервність функції в точці.

Вправи:

Використовуючи графіки функцій (рис. 3) укажіть точки розриву функцій і назвіть проміжки неперервності.

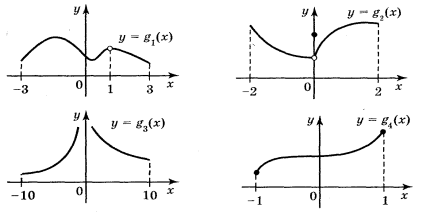
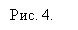Укажіть проміжки неперервності функцій f і g, зображених на рис. 4.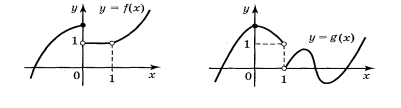

Обернена функція та її графік

Функція, яка приймає кожне своє значення в єдиній точці області визначення, є оборотною.

У такої функції за значенням залежної змінної можна однозначно визначити, якому значенню аргументу воно відповідає.

Інакше кажучи, якщо функція y=f(x) є оборотною й число а належить до її області значень Е(f), то рівняння f(x)=а має розв’язок, причому єдиний.

Оберненою до даної оборотної функції y=f(x) називається така функція x=g(y), яка кожному із множини значень функції y=f(x) ставить у відповідність єдине число x з області визначення.

Функції f і g називають взаємно оберненими, якщо:

D(f)= Е(g) і D(g)= Е(f);
Для будь-якого х₀ 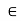D(f) з рівності f(х₀)=у₀ випливає, що g(у₀)= х₀, тобто g(f(х₀))= х₀.

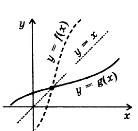$C:\Users\User\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\0_f5084_ff6f725b_orig.png$ Теорема 3. Графіки взаємно обернених функцій симетричні відносно прямої у=х. (Рис. 5)

Рис. 5.

Приклад 7. Знайти функцію, обернену до даної у=2х-1.

Розв’язання. Знаходимо із заданого рівняння:

Замінюючи у цій рівності х на у, а у на х, отримаємо

Контрольні запитання:

Яку функцію називають оборотною?
Як пов’язані область визначення функції та множина значень оберненої до неї функції?
Як пов’язані множина значень функції та область визначення оберненої до неї функції?
Які дві функції називають взаємно оберненими?
Як розташовані графіки взаємно обернених функцій?

Вправи:

Знайдіть функцію, обернену до даної:

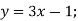
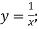
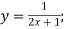
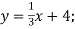
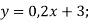
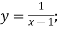
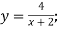
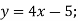
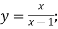
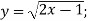
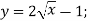
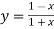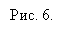
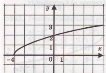Користуючись графіком функції y=f(x), зображеним на рисунку 6, побудуйте графік оберненої до неї функції.

Складена функція

Складеною функцією зазвичай називають функцію від функції.

Якщо змінна y є функцією від u: y = f(u), а u в свою чергу – функцією від x; u = ϕ(x), то y є складеною функцією від x, тобто y = f(ϕ (x)).

Функцію f(u) називають зовнішньою, а ϕ(x) – внутрішньою функцією, або проміжною змінною.

Приклад 8. Запишіть складені функції f(g(x)) і g(f(x)), якщо f(x)= х⁵, а g(x)=3-х.

Розв’язання. f(g(x))=(3-х)⁵; g(f(x))= 3-х⁵.

Контрольні запитання:

Яку функцію називають складеною?
Яку функцію називають внутрішньою функцією?
Яку функцію називають зовнішньою функцією?

Вправи:

Запишіть складені функції f(g(x)) і g(f(x)):

Монотонність функції

Функцію називають зростаючою на деякому проміжку, якщо кожному більшому значенню аргументу із цього проміжку відповідає більше значення функції.

Функцію називають спадною на деякому проміжку, якщо кожному більшому значенню аргументу із цього проміжку відповідає менше значення функції.

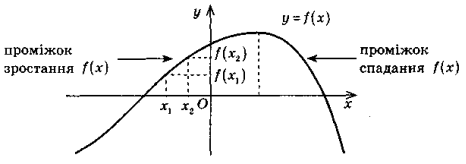
Якщо функція на всій області визначення зростає або на всій області визначення спадає, її називають монотонною. Якщо ж функція зростає на деякому проміжку або спадає на ньому, то говорять, що вона монотонна на даному проміжку.

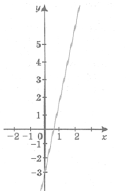
Приклад 9.

Монотонною є функція у = 5х - 3, вона на всій області визначення зростає (рис. 7).

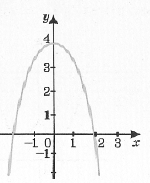Приклад 10.

Функція у=4-х² монотонна на проміжку (-∞; 0), на якому зростає, і на проміжку (0; -∞), на якому спадає. На всій області визначення вона не монотонна (рис. 8).

Приклад 11. Доведіть, що функція спадає на кожному з проміжків (-∞; 0) і (0; +∞).

Розв’язання. Нехай х₁ і х₂ – довільні значення аргументу з проміжку (0; +∞), причому х₁<х₂. Тоді за властивістю числових нерівностей . Отже, дана функція спадає на проміжку (0; +∞).

Аналогічно доводять, що функція спадає на проміжку (-∞; 0).

Контрольні запитання:

Яку функцію називають зростаючою?
Яку функцію називають спадною?
Яку функцію називають монотонною?

Вправи:

Зростаючою чи спадною є функція:

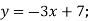
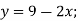
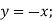
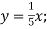
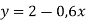Парність і непарність функції

Розглянемо функції, області визначення яких симетричні відносно початку координат, тобто разом з кожним числом x містять і число –x. Для таких функцій визначено поняття парності і непарності.

Функція f називається парною, якщо для будь-якого x з її області визначення f (–x) = f (x).

Приклад 12. Функція y = x²(тобто функція f (x) = x²) - парна, оскільки f (–x) = (–x)² = x² = f (x).

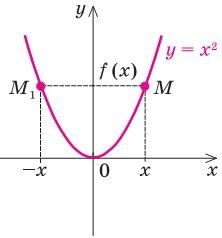Графік парної функції Якщо функція f (x) парна, то до її графіка разом з кожною точкою M з координатами (x; y) = (x; f (x)) входить також і точка M₁ з координатами (–x; y) = (–x; f (–x)) = (–x; f (x)).

Точки M і M₁ розміщені симетрично відносно осі Oy, тому й графік парної функції розміщений симетрично відносно осі Oy. (Рис. 9)

Функція f називається непарною, якщо для будь-якого x з її області визначення f (–x) = –f (x).

Приклад 13. Функція (тобто функція f(x)= ) – непарна, оскільки .

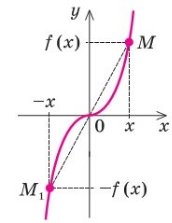
Непарна функція

Якщо функція f (x) непарна, то до її графіка разом з кожною точкою M з координатами (x; y) = (x; f (x)) входить також і точка M₁з координатами (–x; y) = (–x; f (–x)) = (–x; –f (x)).

Точки M і M₁ розміщені симетрично відносно початку координат (рис. 10), тому й графік непарної функції розміщений симетрично відносно початку координат.

Приклад 14. Дослідіть на парність функцію

Розв’язання. Маємо . Отже, область визначення функції симетрична відносно початку координат.

Для будь-якого маємо:

Отже, функція є парною.

Контрольні запитання:

Яку функцію називають парною?
Яку функцію називають непарною?
Сформулюйте властивість графіка парної функції.
Сформулюйте властивість графіка непарної функції.

Вправи:

Доведіть, що є парною функція:

;

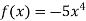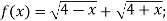
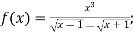
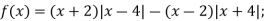
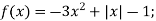
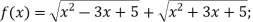
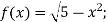
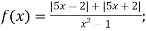
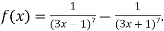
Доведіть, щ є непарною функція:

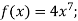
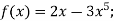
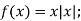
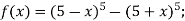
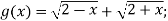
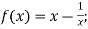
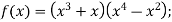
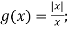
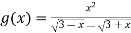Дослідіть на парність функцію:

Парною чи непарною є функція, графік якої зображено на рисунку 11?

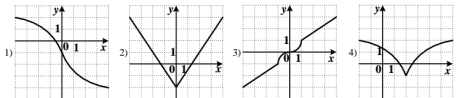
Рис. 11.

Графіки основних елементарних функцій та їх властивості

Графіком числової функції називають геометричну фігуру, яка складається з усіх тих і тільки тих точок координатної площини, абсциси яких дорівнюють значенням аргументу, а ординати відповідним значенням функції.

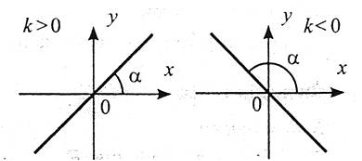
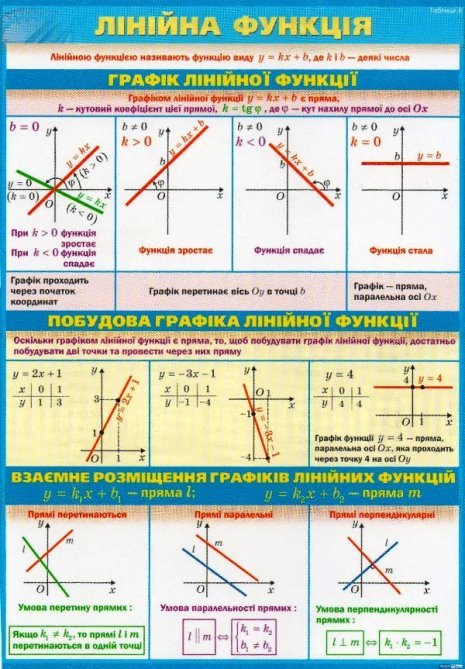
Лінійна функція

Функція

Графіком лінійної функції є пряма, тому для побудови графіка досить побудувати таблицю для двох значень аргументу і функції.

Властивості:

Область визначення лінійної функції – вся числова пряма.
Множина значень лінійної функції – вся числова пряма.
При k>0, функція є зростаючою. При k<0, функція є спадною.

Функція

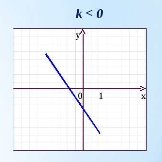
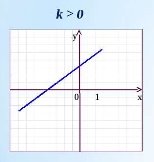
Властивості:

1. Область визначення: R.

2. Функція є непарною.

3. Для $x \in R$ функція зростає, якщо ; спадає, якщо .

4. Область значень: R.

5. Графік – пряма, що проходить через початок координат.

Функція

Властивості:

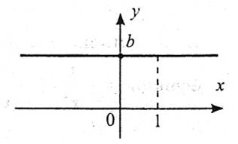
1. Область визначення: R.

2. Функція є парною. Якщо b=0, то функція і парна, і непарна.

3. Для $x \in R$ функція стала.

4. Область значень: {b}.

5. Графік – пряма, паралельна осі х, якщо b≠0, і пряма, що збігається з віссю х, якщо b=0.

Функція $y = \frac{k}{x}\;(y = \frac{k}{{{x^{2n + 1}}}},n \in N,k \ne 0)$

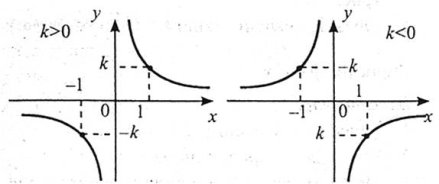
Властивості

1. Область визначення: $x \in ( - \infty ;0) \cup (0; + \infty )$ .

2. Функція є непарною.

3. Якщо , функція спадає на проміжку $( - \infty ;0)$ і на проміжку $(0; + \infty )$ . Якщо , функція зростає на проміжку $( - \infty ;0)$ і на проміжку $(0; + \infty )$ .

4. Область значень: $( - \infty ;0) \cup (0; + \infty )$ .

5. Графік функції – гіпербола.

Функція $y = a{x^2}\;(y = a{x^{2n}},a \ne 0,n \in N)$

Властивості:

1. Область визначення: R.

2. Функція є парною.

3. Якщо , функція спадає на проміжку (-∞;0], зростає на проміжку [0;+∞). Якщо , функція зростає на проміжку (-∞;0], спадає на проміжку [0;+∞).

4. Область значень: якщо , то $y \in [0; + \infty )$ ; якщо , то $y \in ( - \infty ;0]$ .

5. Графік функції – парабола.

Функція $y = a{x^3}\;(y = a{x^{2n + 1}},a \ne 0,n \in N)$

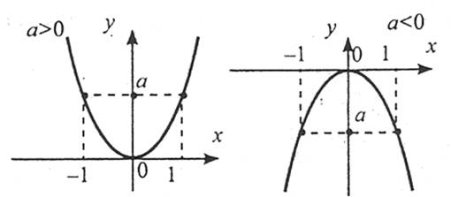
Властивості:

1. Область визначення: R.

2. Функція є непарною.

3. Для $x \in R$ функція зростає, якщо ; спадає, якщо .

4. Область значень: R.

Функція

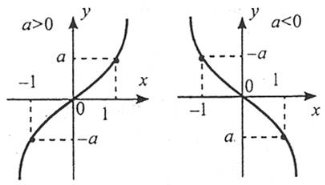
Властивості

1. Область визначення: R.

2. Функція є парною.

3. На проміжку (-∞;0] функція спадає; на проміжку [0;+∞) функція зростає.

4. Область значень: [0;+∞).

Функція $y = \frac{k}{{{x^{2n}}}}\;(y = \frac{k}{{{x^{2n + 1}}}},k \ne 0,n \in N)$

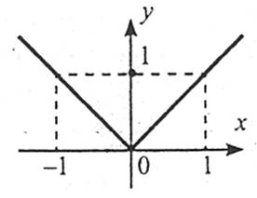
Властивості:

1. Область визначення: $x \in ( - \infty ;0) \cup (0; + \infty )$ .

2. Функція є парною.

3. Якщо , функція зростає на проміжку $( - \infty ;0)$ і спадає на проміжку $(0; + \infty )$ . Якщо , функція спадає на проміжку $( - \infty ;0)$ і зростає на проміжку $(0; + \infty )$ .

4. Область значень: якщо , то $y \in (0; + \infty )$ ; якщо , то $y \in ( - \infty ;0)$ .

Функція $y = \sqrt x$

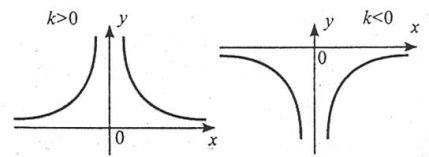
Властивості:

1. Область визначення: [0;+∞).

2. Функція ні парна, ні непарна.

3. На проміжку [0;+∞) функція зростає.

4. Область значень: [0;+∞).

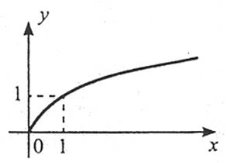
Показникова функція

1. Область визначення - множина R дійсних чисел.

2. Область значень - множина R+ всіх додатних дійсних чисел.

3. При a>1 функція зростає на всій числовій прямій; при 0<a<1 функція спадає на множині R.

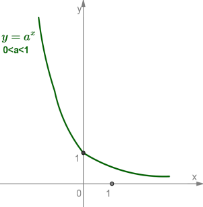
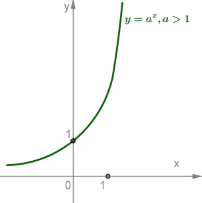
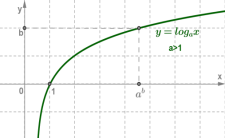
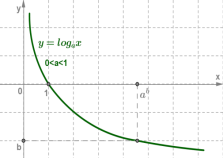
Логарифмічна функція

1. Область визначення логарифмічної функції - множина всіх додатних чисел. D(f)=(0;+∞);

2. Множина значень логарифмічної функції - множина R всіх дійсних чисел. E(f)=(−∞;+∞);

3. Логарифмічна функція на всій області визначення зростає при a>1 або спадає при 0<a<1.

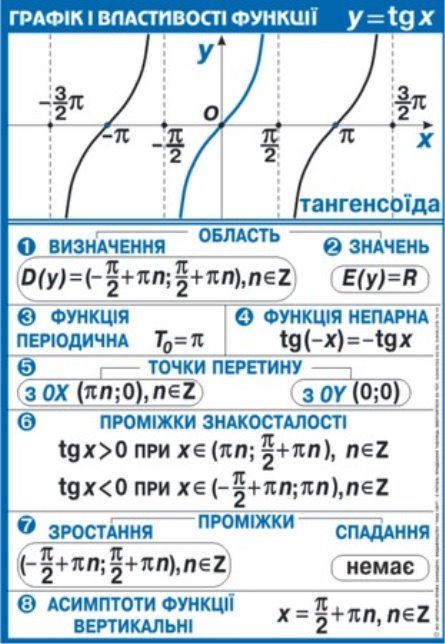
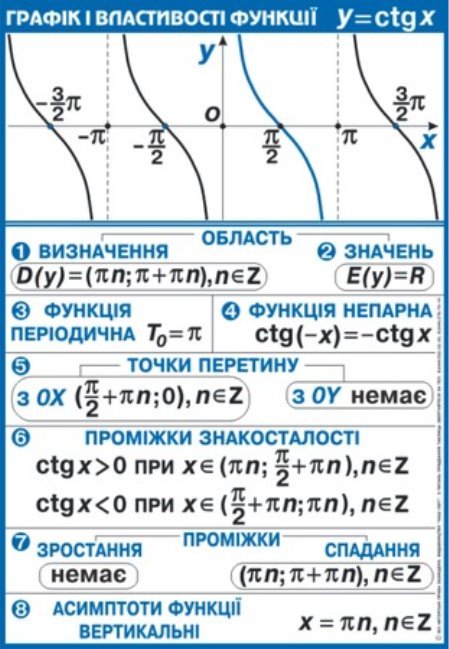
Перетворення графіків функції

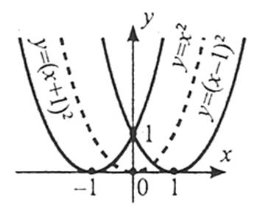
1. Щоб побудувати графік функції , слід перенести графік функції f(x) уздовж осі Ох на а одиниць: вправо, якщо а<0; вліво, якщо а>0.

2. Щоб побудувати графік функції , слід перенести графік функції f(x) уздовж осі Оy на b одиниць: вверх, якщо b<0; вниз, якщо b>0.

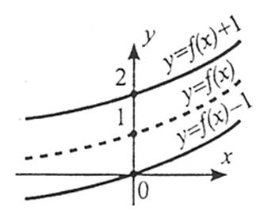
3. Щоб побудувати графік функції , слід графік функції симетрично відобразити відносно осі абсцис.

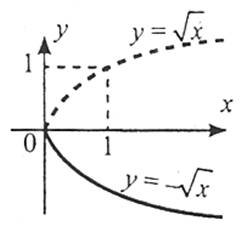
4. Щоб побудувати графік функції , слід графік функції симетрично відобразити відносно осі ординат.

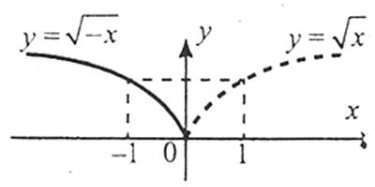
5. Щоб побудувати графік функції , слід частину графіка функції у верхній півплощині і на осі абсцис залишити без змін, а замість частини графіка в нижній півплощині побудувати симетричну їй частину відносно осі Ох.

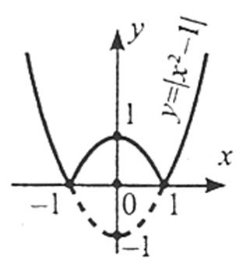
6. Щоб побудувати графік функції , слід частину графіка функції у правій півплощині і на осі ординат залишити без змін, а замість частини графіка в лівій півплощині побудувати симетричну їй частину відносно осі Оу.

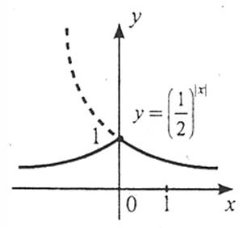
7. Щоб побудувати графік функції , слід:

1) при k>1 стиснути графік функції до точки (0;0) уздовж осі абсцис у k разів;

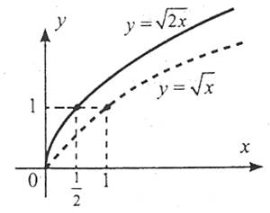
2) при 0<k<1 розтягнути від точки (0;0) графік функції уздовж осі абсцис у $\frac{1}{k}$ разів.

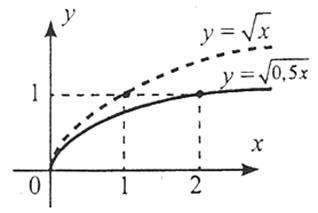
8. Щоб побудувати графік функції , слід:

1) при k>1 розтягнути графік функції до точки (0;0) уздовж осі ординат у k разів;

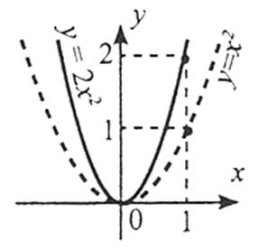
2) при 0<k<1 стиснути від точки (0;0) графік функції уздовж осі ординат у $\frac{1}{k}$ разів.

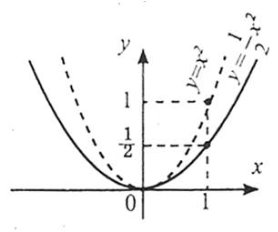
Приклад 15.

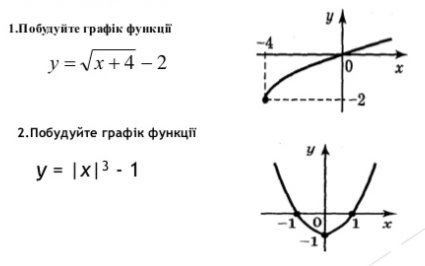
Вчимося
1.Побудуйте графік функції
24  ху
2.Побудуйте графік функції
у = |х|3 - 1

Контрольні запитання:

Як можна отримати графік функції 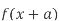, використовуючи графік ?
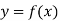Як можна отримати графік функції 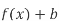, використовуючи графік ?
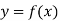Як можна отримати графік функції 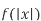, використовуючи графік ?
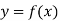Як можна отримати графік функції 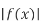, використовуючи графік ?
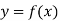Як можна отримати графік функції 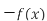, використовуючи графік ?
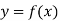Як можна отримати графік функції 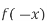, використовуючи графік ?

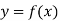Побудуйте графік функції:

;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
.

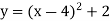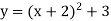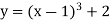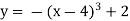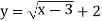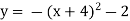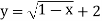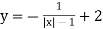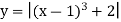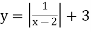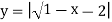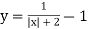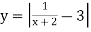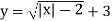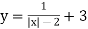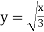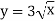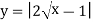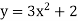Список використаної літератури

Мерзляк А.Г. Алгебра і початки аналізу: підруч. для 10 кл. загальноосвіт. навч. Закладів: академ. рівень / А.Г. Мерзляк, Д.А. Номіровський, В.Б. Полонський, М.С. Якір. – Х.: Гімназія, 2010. 352 с.: іл.
Рудавський Ю.К., Костробій П.П., Мусій Р.С., Веселовська О.В. та ін. Практикум з елементарної математики. Ч.І.: Навч. посібник/За редакцією д-ра фіз.-мат. Наук, проф. Ю.К. Рудавського. – Львів: Видавництво «Бескид Біт», 2002. – 224 с.
Математика для вступників до вузів. Навч. посібник/ Упоряд.: Бондаренко М.Ф., Дікарєв В.А., Мельников О.Ф., Семенець В.В., Шкляров Л.Й. – Харків: «Компанія СМІТ», 2002. – 1120с.

Середня оцінка розробки

Структурованість

5.0

Оригінальність викладу

4.0

Відповідність темі

5.0

Загальна:

4.7

Всього відгуків: 1

Оцінки та відгуки

Музиченко Світлана Василівна 26.04.2022 в 10:08

Загальна:

4.7

Структурованість

5.0

Оригінальність викладу

4.0

Відповідність темі

5.0

docx

Завантажити

Зберегти на потім

Додав(-ла)

Гончарук Світлана Анатоліївна

Пов’язані теми

Алгебра, Методичні рекомендації

Додано

4 травня 2020

Переглядів

27279

Оцінка розробки

4.7 (1 відгук)