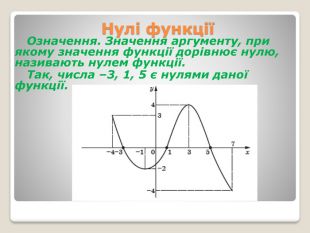
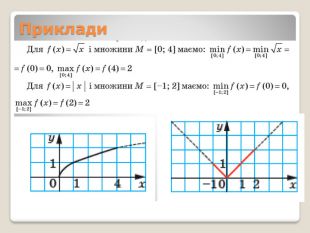
Функції та їх властивості






![Проміжки знакосталостіЗауважимо, що на проміжках [–4; –3) і (1; 5) графік функції f розташований над віссю абсцис, а на проміжках (–3; 1) і (5; 7] — під віссю абсцис. Це означає, що на проміжках [–4; –3) і (1; 5) функція набуває додатних значень, а на проміжках (–3; 1) і (5; 7] — від’ємних. Означення. Проміжок, на якому функція набуває значень однакового знака, називають проміжком знакосталості функції. Проміжки знакосталостіЗауважимо, що на проміжках [–4; –3) і (1; 5) графік функції f розташований над віссю абсцис, а на проміжках (–3; 1) і (5; 7] — під віссю абсцис. Це означає, що на проміжках [–4; –3) і (1; 5) функція набуває додатних значень, а на проміжках (–3; 1) і (5; 7] — від’ємних. Означення. Проміжок, на якому функція набуває значень однакового знака, називають проміжком знакосталості функції.](/uploads/files/318408/251299/270725_images/8.jpg)

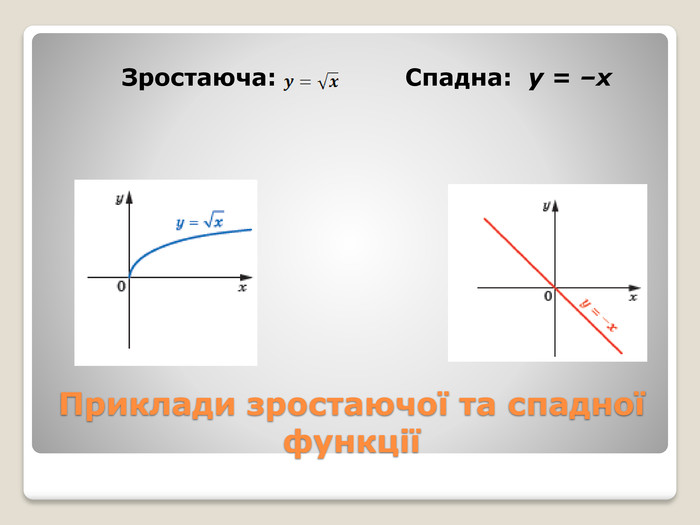
![Зростання функціїЯкщо переміщатися по осі абсцис від –4 до –1, то можна помітити, що графік функції йде вниз, тобто значення функції зменшуються. Кажуть, що на проміжку [–4; –1] функція спадає. Із збільшенням x від –1 до 3 графік функції йде вгору, тобто значення функції збільшуються. Кажуть, що на проміжку [–1; 3] функція зростає. Означення. Функцію f називають зростаючою на множині M ⊂ D (f), якщо для будь-яких двох значень аргументу x1 і x2, які належать множині M, таких, що x1 < x2, виконується нерівність f (x1) < f (x2). Зростання функціїЯкщо переміщатися по осі абсцис від –4 до –1, то можна помітити, що графік функції йде вниз, тобто значення функції зменшуються. Кажуть, що на проміжку [–4; –1] функція спадає. Із збільшенням x від –1 до 3 графік функції йде вгору, тобто значення функції збільшуються. Кажуть, що на проміжку [–1; 3] функція зростає. Означення. Функцію f називають зростаючою на множині M ⊂ D (f), якщо для будь-яких двох значень аргументу x1 і x2, які належать множині M, таких, що x1 < x2, виконується нерівність f (x1) < f (x2).](/uploads/files/318408/251299/270725_images/10.jpg)

![Зростання та спадання функціїОзначення. Функцію f називають зростаючою (спадною) на множині M, якщо для будь-яких значень аргументу з цієї множини більшому значенню аргументу відповідає більше (менше) значення функції. Наприклад, функція y = x2 – 2x (рис. 9) спадає на множині (–∞; 1] і зростає на множині [1; +∞). Зростання та спадання функціїОзначення. Функцію f називають зростаючою (спадною) на множині M, якщо для будь-яких значень аргументу з цієї множини більшому значенню аргументу відповідає більше (менше) значення функції. Наприклад, функція y = x2 – 2x (рис. 9) спадає на множині (–∞; 1] і зростає на множині [1; +∞).](/uploads/files/318408/251299/270725_images/12.jpg)
![Зростання та спадання функціїТакож кажуть, що проміжок (–∞; 1] є проміжком спадання, а проміжок [1; +∞) є проміжком зростання функції y = x2 – 2x. У задачах на пошук проміжків зростання і спадання функції прийнято вказувати проміжки максимальної довжини. Якщо функція зростає на всій області визначення, то її називають зростаючою. Якщо функція спадає на всій області визначення, то її називають спадною. Зростання та спадання функціїТакож кажуть, що проміжок (–∞; 1] є проміжком спадання, а проміжок [1; +∞) є проміжком зростання функції y = x2 – 2x. У задачах на пошук проміжків зростання і спадання функції прийнято вказувати проміжки максимальної довжини. Якщо функція зростає на всій області визначення, то її називають зростаючою. Якщо функція спадає на всій області визначення, то її називають спадною.](/uploads/files/318408/251299/270725_images/13.jpg)

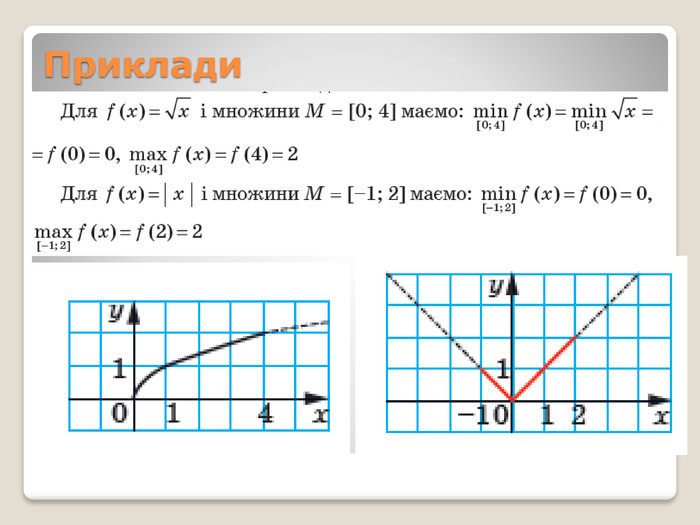


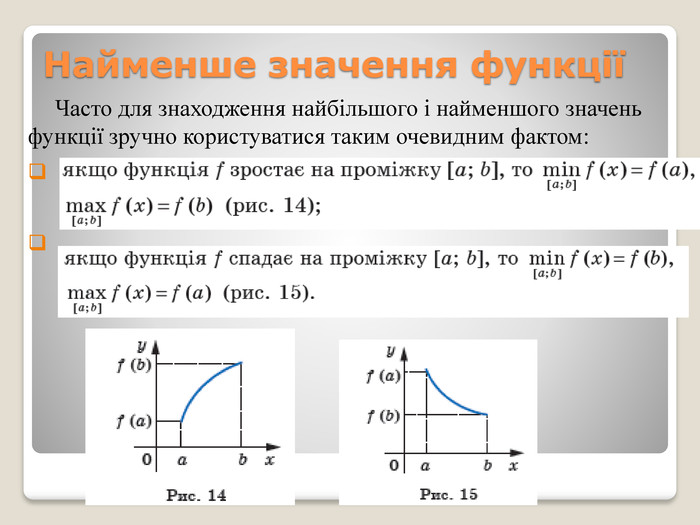



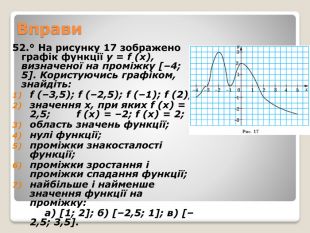
![Вправи52.° На рисунку 17 зображено графік функції y = f (x), визначеної на проміжку [–4; 5]. Користуючись графіком, знайдіть: f (–3,5); f (–2,5); f (–1); f (2); значення x, при яких f (x) = –2,5; f (x) = –2; f (x) = 2; область значень функції; нулі функції; проміжки знакосталості функції; проміжки зростання і проміжки спадання функції; найбільше і найменше значення функції на проміжку: а) [1; 2]; б) [–2,5; 1]; в) [–2,5; 3,5]. Вправи52.° На рисунку 17 зображено графік функції y = f (x), визначеної на проміжку [–4; 5]. Користуючись графіком, знайдіть: f (–3,5); f (–2,5); f (–1); f (2); значення x, при яких f (x) = –2,5; f (x) = –2; f (x) = 2; область значень функції; нулі функції; проміжки знакосталості функції; проміжки зростання і проміжки спадання функції; найбільше і найменше значення функції на проміжку: а) [1; 2]; б) [–2,5; 1]; в) [–2,5; 3,5].](/uploads/files/318408/251299/270725_images/25.jpg)



![Самостійне виконання вправи67.° Накресліть графік якої-небудь функції, визначеної на проміжку [–5; 4], яка: зростає на проміжку [–5; 1] і спадає на проміжку [1; 4]; спадає на проміжках [–5; –1] і [2; 4] та зростає на проміжку [–1; 2]. Самостійне виконання вправи67.° Накресліть графік якої-небудь функції, визначеної на проміжку [–5; 4], яка: зростає на проміжку [–5; 1] і спадає на проміжку [1; 4]; спадає на проміжках [–5; –1] і [2; 4] та зростає на проміжку [–1; 2].](/uploads/files/318408/251299/270725_images/29.jpg)






Функція та її основні властивості У повсякденному житті нам часто доводиться спостерігати процеси, у яких зміна однієї величини (незалежної змінної) призводить до зміни іншої величини (залежної змінної). Вивчення цих процесів потребує створення їх математичних моделей. Однією з таких найважливіших моделей є функція. Нехай X — множина значень незалежної змінної, Y — множина значень залежної змінної. Функція — це правило, за допомогою якого за кожним значенням незалежної змінної з множини X можна знайти єдине значення залежної змінної з множини Y. Зазвичай незалежну змінну позначають буквою x, залежну — буквою y, функцію (правило) — буквою f. Кажуть, що змінна y функціонально залежить від змінної x. Цей факт позначають так: y = f (x). Незалежну змінну ще називають аргументом функції.
Функція та її основні властивості Множину значень, яких набуває аргумент, тобто множину X, називають областю визначення функції і позначають D (f) або D (y). Наприклад, областю визначення функції є множина D (y) = (–∞; –1) (–1; 1) (1; +∞). Множину значень, яких набуває залежна змінна y, тобто множину Y, називають областю значень функції і позначають E (f) або E (y). Наприклад, областю значень функції y = x2 + 1 є множина E (y) = [1; +∞).
Функція та її основні властивості Елементами множин D (f) і E (f) можуть бути об’єкти найрізноманітнішої природи. Так, якщо кожному многокутнику поставити у відповідність його площу, то можна говорити про функцію, область визначення якої — множина многокутників, а область значень — множина додатних чисел. Якщо кожній людині поставити у відповідність день тижня, у який вона народилася, то можна говорити про функцію, область визначення якої — множина людей, а область значень — множина днів тижня. Коли D (f) ⊂ R і E (f) ⊂ R, функцію f називають числовою. Функцію вважають заданою, якщо вказано її область визначення і правило, за яким за кожним значенням незалежної змінної з області визначення можна знайти значення залежної змінної з області значень.
Задання функціїФункцію можна задати одним з таких способів: описово; за допомогою формули; за допомогою таблиці; графічно. Найчастіше функцію задають за допомогою формули. Якщо при цьому не вказано область визначення, то вважають, що областю визначення функції є область визначення виразу, який входить до формули. Наприклад, якщо функція f задана формулою то її областю визначення є область визначення виразу тобто проміжок (1; +∞).
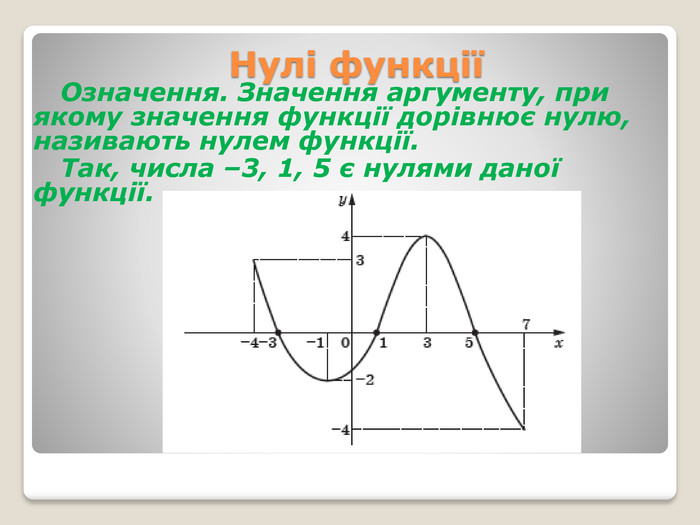
Графік функціїОзначення. Графіком числової функції f називають геометричну фігуру, яка складається з усіх тих і тільки тих точок координатної площини, абсциси яких дорівнюють значенням аргументу, а ординати — відповідним значенням функції f. Сказане означає, що коли якась фігура є графіком функції f, то виконуються дві умови: якщо x0 — деяке значення аргументу, а f (x0) — відповідне значення функції, то точка з координатами (x0; f (x0)) належить графіку; якщо (x0; y0) — координати довільної точки графіка, то x0 і y0 — відповідні значення незалежної і залежної змінних функції f, тобто y0 = f (x0).
Проміжки знакосталостіЗауважимо, що на проміжках [–4; –3) і (1; 5) графік функції f розташований над віссю абсцис, а на проміжках (–3; 1) і (5; 7] — під віссю абсцис. Це означає, що на проміжках [–4; –3) і (1; 5) функція набуває додатних значень, а на проміжках (–3; 1) і (5; 7] — від’ємних. Означення. Проміжок, на якому функція набуває значень однакового знака, називають проміжком знакосталості функції.
Проміжки знакосталостіНаприклад, проміжки (–∞; 0) і (0; +∞) є проміжками знакосталості функції y = x2. Зауваження. Під час пошуку проміжків знакосталості функції прийнято вказувати проміжки максимальної довжини. Наприклад, проміжок (–2; –1) є проміжком знакосталості функції f (рис. 8), але до відповіді увійде проміжок (–3; 1), який містить проміжок (–2; –1).
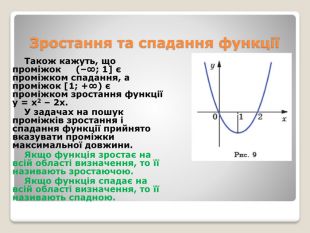
Зростання функціїЯкщо переміщатися по осі абсцис від –4 до –1, то можна помітити, що графік функції йде вниз, тобто значення функції зменшуються. Кажуть, що на проміжку [–4; –1] функція спадає. Із збільшенням x від –1 до 3 графік функції йде вгору, тобто значення функції збільшуються. Кажуть, що на проміжку [–1; 3] функція зростає. Означення. Функцію f називають зростаючою на множині M ⊂ D (f), якщо для будь-яких двох значень аргументу x1 і x2, які належать множині M, таких, що x1 < x2, виконується нерівність f (x1) < f (x2).
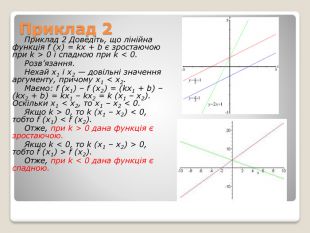
Зростання та спадання функціїОзначення. Функцію f називають зростаючою (спадною) на множині M, якщо для будь-яких значень аргументу з цієї множини більшому значенню аргументу відповідає більше (менше) значення функції. Наприклад, функція y = x2 – 2x (рис. 9) спадає на множині (–∞; 1] і зростає на множині [1; +∞).
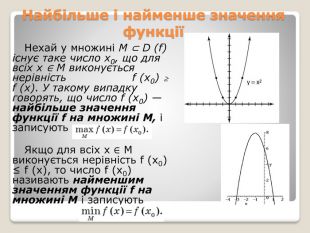
Зростання та спадання функціїТакож кажуть, що проміжок (–∞; 1] є проміжком спадання, а проміжок [1; +∞) є проміжком зростання функції y = x2 – 2x. У задачах на пошук проміжків зростання і спадання функції прийнято вказувати проміжки максимальної довжини. Якщо функція зростає на всій області визначення, то її називають зростаючою. Якщо функція спадає на всій області визначення, то її називають спадною.
Приклад 1 Приклад 1 Доведіть, що функція спадає на кожному з проміжків (–∞; 0) і (0; +∞). Розв’язання. Нехай x1 і x2 — довільні значення аргументу з проміжку (0; +∞), причому x1 < x2. Тоді за властивістю числових нерівностей . Отже, дана функція спадає на проміжку (0; +∞). Аналогічно доводять, що функція f спадає на проміжку (–∞; 0). Зауважимо, що не можна стверджувати, що дана функція спадає на всій області визначення D (f) = (–∞; 0) (0; +∞), тобто є спадною. Дійсно, якщо, x1 < x2 не випливає, що .
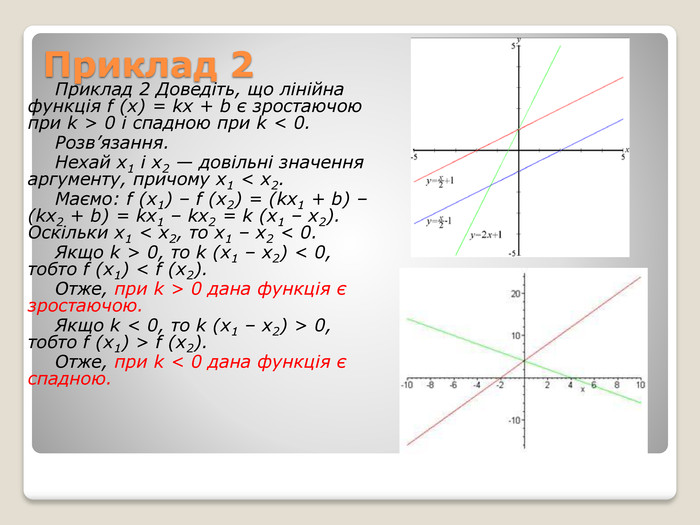
Приклад 2 Приклад 2 Доведіть, що лінійна функція f (x) = kx + b є зростаючою при k > 0 і спадною при k < 0. Розв’язання. Нехай x1 і x2 — довільні значення аргументу, причому x1 < x2. Маємо: f (x1) – f (x2) = (kx1 + b) – (kx2 + b) = kx1 – kx2 = k (x1 – x2). Оскільки x1 < x2, то x1 – x2 < 0. Якщо k > 0, то k (x1 – x2) < 0, тобто f (x1) < f (x2). Отже, при k > 0 дана функція є зростаючою. Якщо k < 0, то k (x1 – x2) > 0, тобто f (x1) > f (x2). Отже, при k < 0 дана функція є спадною.
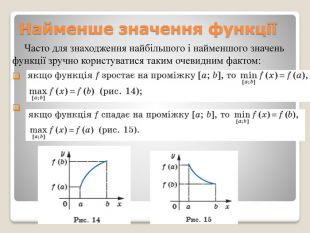
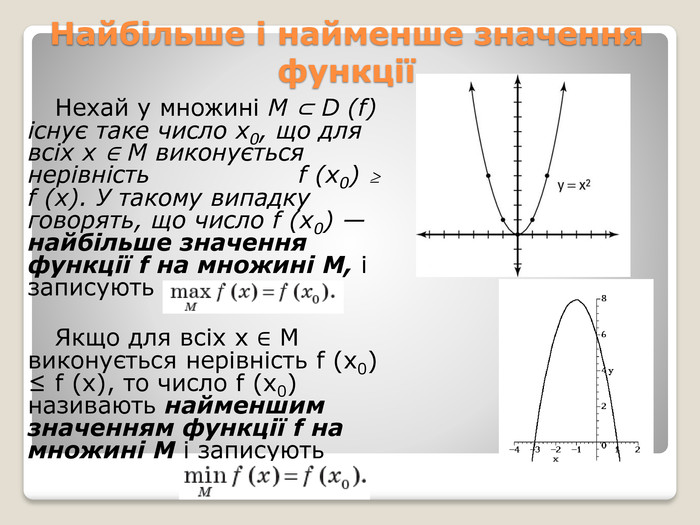
Найбільше і найменше значення функціїНехай у множині M ⊂ D (f) існує таке число x0, що для всіх x ∈ M виконується нерівність f (x0) ≥ f (x). У такому випадку говорять, що число f (x0) — найбільше значення функції f на множині M, і записують Якщо для всіх x ∈ M виконується нерівність f (x0) ≤ f (x), то число f (x0) називають найменшим значенням функції f на множині M і записують
Первинне закріплення вивченого матеріалу1 . Що таке функція? 2 . Що називають аргументом функції? 3 . Що називають областю визначення функції? 4 . Що називають значенням функції? 5 . Що називають областю значень функції? 6 . Що треба вказати, щоб функція вважалася заданою? 7 . Які способи задання функції ви знаєте? 8 . Що вважають областю визначення функції, якщо вона задана формулою і при цьому не вказано область визначення? 9 . Що називають графіком числової функції? 10. Яке значення аргументу називають нулем функції? 11. Поясніть, що називають проміжком знакосталості функції. 12. Яку функцію називають зростаючою на множині? 13. Яку функцію називають спадною на множині? 14. Яку функцію називають зростаючою? 15. Яку функцію називають спадною? 16. Поясніть, що називають найбільшим (найменшим) значенням функції на множині. 17. Як записують, що число f(x0) є найбільшим (найменшим) значенням функції f на множині M?
Вправи46.° Функцію задано формулою f (x) = –3x2 + 2x. Знайдіть: f (1); f (0); f (1/3); f (–2). Знайдіть значення аргументу, при якому значення функції дорівнює: 0; –1; –56. Чи є правильною рівність: f (–1) = 5; f (2) = –8?47.° Функцію задано формулою Знайдіть: f (4); f (0); f (9); f (–3). Знайдіть значення x, при якому: f (x) = 9; f (x) = 0,5; f (x) = –10. 48.° Кожному натуральному числу, більшому за 15, але меншому від 25, поставили у відповідність остачу від ділення цього числа на 4. Яким способом задано цю функцію? Яка область значень цієї функції? Задайте дану функцію таблично.
Вправи52.° На рисунку 17 зображено графік функції y = f (x), визначеної на проміжку [–4; 5]. Користуючись графіком, знайдіть: f (–3,5); f (–2,5); f (–1); f (2); значення x, при яких f (x) = –2,5; f (x) = –2; f (x) = 2; область значень функції; нулі функції; проміжки знакосталості функції; проміжки зростання і проміжки спадання функції; найбільше і найменше значення функції на проміжку: а) [1; 2]; б) [–2,5; 1]; в) [–2,5; 3,5].
Тренувальні вправи73. Задайте формулою яку-небудь функцію, областю визначення якої є: 1) множина дійсних чисел, крім чисел –2 і 3; 2) множина дійсних чисел, не більших за 3; 3) множина дійсних чисел, не менших від –4, крім числа 5; 4) множина, яка складається з одного числа –1. 74. Задайте формулою яку-небудь функцію, областю визначення якої є: множина дійсних чисел, крім чисел –1, 0 і 1; множина дійсних чисел, менших від 7; множина дійсних чисел, не менших від 2, крім чисел 5 і 6. 75. Чи є правильним твердження: будь-яка пряма, паралельна осі ординат, перетинає графік будь-якої функції в одній точці; пряма, паралельна осі абсцис, може не перетинати графік функції; пряма, паралельна осі ординат, не може перетинати графік функції більше ніж в одній точці; існують функції, графік яких симетричний відносно осі ординат; існують функції, графік яких симетричний відносно осі абсцис; існують функції, графік яких симетричний відносно початку координат?
-
 Левадній Сергій Павлович 13.03.2023 в 17:30Загальна:4.7Структурованість5.0Оригінальність викладу4.0Відповідність темі5.0
Левадній Сергій Павлович 13.03.2023 в 17:30Загальна:4.7Структурованість5.0Оригінальність викладу4.0Відповідність темі5.0


про публікацію авторської розробки
Додати розробку