Функція. Область визначення та область значень функції

Тема. Функція. Область визначення та область значень функції

Мета: домогтися усвідомлення учнями змісту понять «функція», «функціональна залежність», «область визначення функції», «область зна­чень функції», способи задання функції; здійснити первинне закріплення змісту вивчених понять; розпочати роботу з вироблення вмінь: а) задавати функціональні залежності формулами; б) працювати із функціями, зада­ними таблицею; в) обчислювати за формулою значення функції, якщо відомо значення аргументу, та розв'язувати обернену задачу.

Тип уроку: засвоєння нових знань.

Хід уроку

I. Організаційний момент

Учитель перевіряє готовність учнів до уроку.

 Учитель повідомляє учням про результати тематичної контрольної роботи.

II. Перевірка домашнього завдання

1. Зошити з виконаним аналізом тематичної контрольної роботи та корекцією учні здають на перевірку.

2. Робота з випереджальним домашнім завданням.

Завдання:

1. Складіть вираз для обчислення площі S квадрата зі стороною а.
2. За складеним виразом знайдіть S, якщо а = 1; 0,2; .
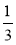3. За складеною формулою знайдіть а, якщо S = 1; 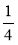; 0,25.
4. Яких значень можуть набувати змінні S та а у виразі (якщо врахувати, що а та S — довжина сторони квадрата та його площа відповідно)?

Учні самостійно виконують завдання, роблять записи:

1. Формула S = а².
2. Якщо а = 1, то S = 1² = 1; якщо а = 0,2, то S = 0,2² = 0,04; якщо а = 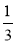, то .
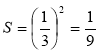3. S = 1, якщо а = 1; S = 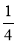, якщо а = 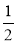; S = 0,25, якщо а = 0,5.

 (Якщо в учнів виникають труднощі під час виконання цієї частини завдання, слід показати їм, що, по-перше, а за умовою — сторона квадрата, тому може виражатися лише додатним числом і, по-друге, для знаходження а за відомою S необхідно «підібрати» таке число, щоб виконувалась рівність а² = S.)

     4) Оскільки а — довжина сторони, a S — площа квадрата, то а > 0, S > 0.

Після перевірки здобутих відповідей, спонукаємо учнів до висновків, серед яких виділяємо ті, що будуть основою для формулювання мети уро­ку й формування нових знань учнів, а саме:

5) залежність (як тлумачиться у словнику):

Співвідношення між двома величинами може виражатись формулою, причому ця формула допомагає знаходити будь-яку з цих двох величин через відому іншу шляхом певних обчислень.

Кожна з двох букв, що входять у формулу, може набувати значень, зу­мовлених, наприклад, змістом самих змінних.

Кожному значенню однієї змінної, що входить до складу формули, може відповідати єдине значення іншої змінної.

Співвідношенню між змінними а і S у цьому прикладі відповідає одне зі значень слова «залежність».

III. Формулювання мети й цілей уроку

Мотивація навчальної діяльності

 Слово вчителя. Виявляється, що як і в щоденному житті, так і в науці часто зустрічаються залежності між двома змінними, які можна ви­разити формулами або іншими способами, і властивості таких за­лежностей дуже схожі на той приклад, що ми розглянули. Тому на сьогоднішньому уроці ми нарешті з'ясуємо, як такі залежності ви­значаються в математиці, які математичні поняття пов'язані із цим поняттям, а також навчимося розв'язувати контрольні завдання на закріплення змісту позначених понять.

IV. Актуалізація опорних знань

Виконання усних вправ

1. Площа прямокутника зі сторонами 9 см та х см дорівнює S см². Виразіть формулою залежність S від х.
2. Потяг рухається зі швидкістю 70 км/год. За t годин він долає S км. За­дайте формулою залежність S від t.
3. Нехай а см — довжина ребра куба, a V см³ — його об'єм. Задайте форму­лою залежність V від а.
4. При яких значеннях змінної має зміст вираз: 3 – х; ; ?

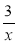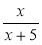V. Вивчення нового матеріалу

 Зміст навчального матеріалу з теми «Функція» до недавнього часу був обов'язковим для розгляду в 7 класі на уроках алгебри (останні кілька років цей матеріал був перенесений до 8 класу). Традиційно функція трактується як залежність однієї змінної від іншої, за якої кожному значенню однієї змінної відповідає значення іншої змін­ної Такий підхід до введення поняття функції вже підготовлений розглядом різних прикладів реальних залежностей між величинами Учні повинні усвідомити зміст понять «область визначення функ­ції», «область значень функції», «аргумент» («незалежна змінна»), «значення функції» («залежна змінна»), поступово вони повинні призвичаїтися до висловів типу «Площа квадрата є функцією його сторони»  Корисно підкреслити, що термін «функція» використо­вується у двох значеннях — як сама залежність та як значення залежної змінної Також хотілося б сказати, що учні, маючи все ж таки схильність до предметного мислення, краще засвоюють цей абстрактний матеріал, якщо подати достатню кількість прикладів.

У цьому місці курсу алгебри, згідно з новою Програмою, виділяється окреме питання «Способи задання функції» як спеціального предмета вивчення Тому, пояснивши, що задати функцію означає вказати спосіб, що дозволяє для будь-якого значення аргументу знайти відповідне зна­чення функції, необхідно ще виділити, які саме способи задання функції найчастіше використовуються на практиці

План викладання навчального матеріалу можна запропонувати такий

1. Уявлення про залежність (відповідність) між двома змінними Незалеж­на змінна Залежна змінна.
2. Функціональні залежності Функції Аргумент та значення функції.
3. Способи задання функції а) таблицею, б) формулою, в) графічно, г) опис.
4. Область визначення та область значень функції.
5. Приклад Функція задана формулою у = 5х

1) Яка змінна є аргументом? [x] 2) Яка змінна є залежною? [у]

3) Яке значення функції відповідає аргументу - 2?

  [Якщо х = -2, то y = 5 ∙ (-2) = -10]

4) Якому значенню аргументу відповідає значення функції у = 0,5? [у = 0,5, отже, 0,5 = 5х, х = 0,5 : 5]

Висновки. Дві найтиповіші задачі для функції за відомим значенням аргументу відшукати відповідне значення функції — та обернена знайти аргумент, що відповідає заданому значенню функції.

VI. Первинне закріплення

Виконання усних вправ

1. Відповідності задані таблицями

Які з цих відповідностей є функціями?

Для функціональних залежностей назвіть пари відповідних значень аргументу та функції Яка область визначення цієї функції? область зна­чень кожної з цих функцій?

Чи зможете ви задати ці функції формулою?

Виконання письмових вправ

1. Одна сторона прямокутника дорівнює 6 см а друга х см. За якою фор­мулою можна обчислити площу S прямокутника? Чи задає ця форму та функцію⁹ Якщо так, укажіть кілька значень її аргументу та відшукайте за формулою відповідні значення функції.
2. Автомобіль рухається зі швидкістю 75 км/год. За час t год він долає відстань 5 км. Задайте залежність між t і S формулою. Знайдіть значення функції, якщо t = 2,4 При якому значенні аргументу функція набуває значення S = 150?
3. Функція задана формулою у = 2х² + 1. Складіть таблицю значень функції для значень аргументу -4; -2; 0; 2; 4.
4. Функція задана формулою у = 4х – 5. Складіть таблицю значень аргу­менту, яким відповідають значення функції 0; 3; 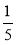; 0,7.
5. Функція задана таблицею

1) Знайдіть значення функції при х = -2; х = 2.

2) При яких значеннях аргументу, значення функції дорівнює -1, 1?

3) Яка область визначення функції?

4) Яка область значень функції?

5*) Яким рівнянням можна було б задати цю функцію?

VII. Підсумки уроку

Використовуючи план уроку (записаний на дошці), учні обмінюються здобутою інформацією, з'ясовують, яка частина навчального матеріалу була найскладнішою, яка найпростішою, яке поняття слід доопрацювати вдома

VIII. Домашнє завдання

Вивчіть означення основних понять уроку, виконайте завдання:

№1 Функцію задано формулою у = 2х² – 7х + 1. Знайдіть значення функції, що відповідає значенню аргументу 1; -2; 0,3; ; 0.

№ 2. Функцію задано формулою у = 0,1х + 5. Для значення аргументу, що дорівнює 10; 50; 120 відшукайте відповідні значення функції.

№ 3. Випереджальне домашнє завдання.

1) За підручником або конспектом повторіть, що таке область допус­тимих значень.

Відшукайте ОДЗ виразу .

2) Нехай функцію задано формулою .

Чи можна знайти значення функції, якщо аргумент дорівнює -5; -3; 0. Чому? Яке з наведених чисел не буде входити в область визначення функції? Порівняйте свою відповідь з п. 1). Зробіть висновки.