Розробка уроку на тему "Графік функції"

Тема. Графік функції

Мета: сформувати в учнів свідоме розуміння поняття «графік функції» та розпочати роботу із засвоєння вмінь читати та будувати графіки функції; розвивати просторове мислення, відпрацювати обчислювальні навички.

Тип уроку: засвоєння нових знань.

Хід уроку

I. Організаційний момент

II. Перевірка домашнього завдання

 1) Особливу увагу під час перевірки домашнього завдання слід приділити № 1 (в), розв'язання якого зводиться до складання та розв'язування рівняння, де замість у підставляємо х, якщо функція дорівнює аргументу, або 3х, якщо функція в 3 рази більша за аргу­мент.

2) Під час роботи з випереджальним домашнім завданням слід звернути увагу на такі моменти:

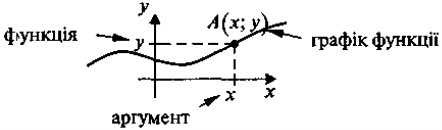
а) якщо функція задана формулою, то можна скласти як завгодно багато пар значень (х; у), де х — значення аргументу; у — відповідне значення
функції;

б) з 6-го класу учням відомо, що пара (х; у) зображується точкою на координатній площині, де х та у, відповідно, абсциса та ордината цієї точки;

в) з п. а) та б) випливає, що для кожної функції можна побудувати, взагалі кажучи, як завгодно багато точок (х; у), де х — аргумент, а у — відповідне значення функції.

III. Формулювання мети й завдань уроку

Зі сказаного вище випливає запитання: навіщо це потрібно робити, тобто який зиск ми можемо мати в такій побудові і яке поняття, пов'язане із функцією, ми будемо розглядати.

IV. Актуалізація опорних знань
Виконання усних вправ

1. Як розташована точка А на координатній площині (вище від осі х, ниж­че від осі х, на осі х), якщо:

1) А (3; 7); 2) А (-5; 4); 3) А (-3; -6); 4) А(1; 0)?

2. Кінцями відрізка є точки А(-2; 6) та В(1; 3). Чи перетинає відрізок АВ вісь х? вісь у?
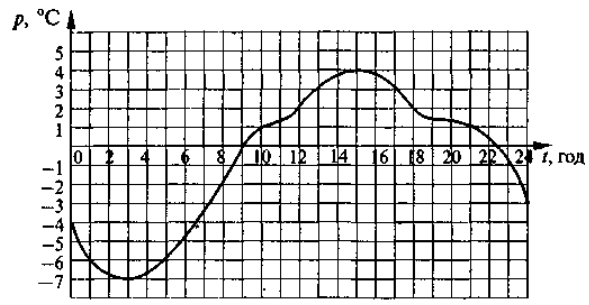
3. Використовуючи графік температури повітря (див. рис), дайте відпо­відь на запитання: а) яка температура повітря була о 8, о 12, о 20 год; б) коли температура була 5°С, -4°С, 1°С; в) коли температура була 0 °С, коли вона була вищою за 0°С і коли була нижчою 0°С; г) коли температура була найменшою і коли найбільшою?

Отже, ми повторили:

1) що показують координати точки в координатній площині;

2) як знайти координати заданої точки та як побудувати точку із відомими координатами в координатній площині;

3) що називається графіком залежності? що показує графік? що можна
дізнатись, розглянувши графік залежності?

V. Засвоєння знань

 Викладення змісту поняття «графік функції» можна розпочати із виконання усних вправ (див. вище АОЗ з № 3). Конкретний реаль­ний сюжет цієї вправи формує в учнів змістовні уявлення, на основі яких легко, сформувати уявлення про графік довільної числової функції. Після цього можна сформулювати означення графіка числової функції та розглянути приклади, що формують в учнів уяв­лення про сферу застосування (вид задач на використання змісту поняття) графіка функції.

Записи в зошитах учнів можуть мати такий вигляд:

VI. Засвоєння практичних умінь

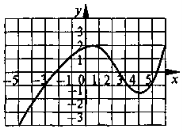
Приклад 1. Використовуючи графік фун­кції (див. рис):

а) Заповніть таблицю.

г) При яких значеннях х функція додатна? від'ємна?

Приклад 2. Чи залежать точки А(4; 2), В(1; -4), С(1; 4) графіку функ­ції, що задана формулою у = 2х – 6? Назвіть координати ще будь-яких 2-х точок, одна з яких належить графіку цієї функції, а інша — не належить.

Приклад 3. Побудуйте графік функції, що задана формулою у = х(х – 3), заповнивши попередньо таблицю:

Приклад 4. Побудуйте графік функції, що задана формулою:

1. у = х + 3, 1 ≤ х ≤ 5; 2) у = 4 – х²; -3 ≤ х ≤ 3.

 Оскільки вправи 3 – 4 є досить складними для учнів, тому не всі вправи (серед прикладів 3 та 4) є обов'язковими для виконання.

VII. Підсумки уроку
Контрольні запитання

1. Сформулюйте означення графіка функції.
2. Як за допомогою графіка функції за заданим значенням аргумента знайти відповідне значення функції і за заданим значенням функції знайти значення аргументу, якому він відповідає?

VIII. Домашнє завдання

№ 1. Вивчіть зміст основних понять уроку.

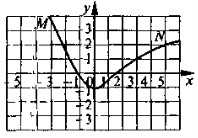№ 2. Крива MN — графік деякої функції. Знайдіть за графіком: а) значення функції, що відповідають значенням аргументу -2; -1; 0; 1; 5;      б) при яких значеннях аргументу функ­ція дорівнює 0; в) при яких значеннях аргу­менту функція набуває додатних значень, від'ємних значень; г) яка область визначення функції, яка область значень функції?

№ 3. Чи належать точки А(3; -1), В 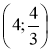графіку функції ?

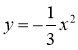№ 4. Побудуйте ламану ABC: А(-3; 1), В(-1; -1), С( 3; 3). Чи можна вва­жиш цю ламану графіком деякої функції? Чому?