Функція. Область визначення та область значень функції
Тема. Функція. Область визначення та область значень функції
Мета: вдосконалювати та поглиблювати вміння та навички розв'язувати основні види завдань для функції, заданої формулою.
Тип уроку: застосування знань.
Хід уроку
I. Організаційний момент
II. Перевірка домашнього завдання
1) № 1,2 перевіряємо, зібравши зошити, № 2 бажано розібрати (навести приклади і сформулювати основну ідею, найбільш вдалі роботи можна оцінити).
2) № 3 (випереджальне домашнє завдання) розбираємо ретельно, бо ці вправи є основою для розв'язування вправ високого рівня, запланованих на уроках.
Завдання 1. Поясніть хід розв'язання рівнянь:
1) х2 – 2х + 1 = 0; 2) х2 – 2х = 0; 3) х2 + 1 = 0, 4) |х – 3| = 0; 5) |х – 3| + 1 = 0.
Які корені мають рівняння? Що це означає?
Завдання 2. Поясніть, як, використавши результати завдання 1, знайти значення змінної х, при яких виконуються нерівності:
1) х2 – 2х + 1 ≠ 0; 2) х2 – 2х ≠ 0; 3) х2 + 1 ≠ 0; 4) |х – 3| ≠ 0; 5) |х – 3| + 1 ≠ 0.
Висновок. Бажано, щоб учні усвідомили, що розв'язки нерівності вигляду f(х) ≠ 0 можна знайти, розв'язавши рівняння f(х) = 0 і виключивши із множини всіх (раціональних) чисел знайдені корені рівняння.
III. Формулювання мети й завдань уроку
Основна мета уроку — вдосконалити вміння та навички знаходження за формулою значення функції, а також поглибити ці вміння, розв'язавши задачі високого рівня.
IV. Актуалізація опорних знань
Виконання усних вправ
- Укажіть область визначення функції, яку задано формулою:
1) у = 2х; 2) у = 3х + 4; 3) 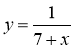 .
.
-
Знайдіть значення функції, яку задано формулою
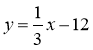 , що відповідає значенню аргументу: -6; 12; 0; 1,5.
, що відповідає значенню аргументу: -6; 12; 0; 1,5.
-
Функцію задано формулою: 1) у = 1,3х; 2)
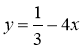 .
.
Знайдіть значення аргументу, якому відповідає значення функції, що дорівнює 0.
V. Удосконалення та поглиблення знань, умінь
На цьому уроці, коли основні поняття, пов'язані з поняттям функції, вже засвоєні і базові вміння щодо розв'язування основних задач для функції сформовані, основну увагу приділяємо розв'язуванню завдань достатнього і високого рівнів, які б поєднували новий матеріал із вивченим раніше матеріалом. Якщо рівень підготовки учнів досить високий, можна розширити знання учнів, ознайомивши їх із кусковим способом задання функції.
Виконання письмових вправ
- Знайдіть область визначення функції, заданої формулою:
1) 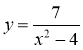 ; 2)
; 2) 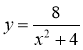 ; 3)
; 3) 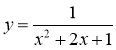 ; 4)
; 4) 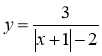 ;
;
5*) 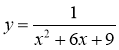 .
.
2*. Функція задана кусково:
 1)
1) 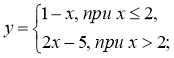 2)
2) 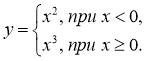
Знайдіть значення функції, що відповідає значенню аргументу, що дорівнює -2; 0; 3.
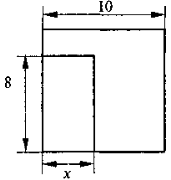
- Від квадрата зі стороною 10 см відрізали прямокутник зі сторонами 8 см і х см (див.рис). Позначивши площу частини, що залишилась (у см2), буквою у, виразіть залежність у від х формулою. Знайдіть:
- значення у, якщо х = 2,5;
- значення х, при якому у = 20; 36;
- область визначення цієї функції.
4*. Знайдіть найменше значення функції у = х2 – 4х + 2.
5*. Доведіть, що функція 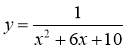 не може набувати від'ємних значень. Яка область визначення функції? Якого найбільшого значення набуває функція?
не може набувати від'ємних значень. Яка область визначення функції? Якого найбільшого значення набуває функція?
6*. Додатково (на повторення). Встановіть пропущене число.
|
ху + 3х2 |
|
5 |
|
х3 – 2у |
|
? |
VI. Підсумок уроку
Контрольні запитання
- Наведіть приклад функціональної відповідності між числами.
- Поясніть на прикладі, що таке аргумент і що таке функція.
- Які ви знаєте способи задання функції?
- Що називають областю визначення та областю значень функції?
VII. Домашнє завдання
Повторіть зміст основних понять теми (див. контрольні запитання).
№ 1. Функцію задано формулою у = 5х – 3.
1) Знайдіть значення функції, які відповідають значенням аргументу -8; 0; 16.
2) Знайдіть значення аргументу, якому відповідає значення функції: -3; 1.
3) При якому значенні означення функції дорівнює значенню аргументу? в 3 рази більше за значення аргументу?
№ 2. Розгляньте функцію 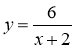 , де -1 ≤ х ≤ 4. Знайдіть пари значень х та у для всіх цілих значень х та запишіть їх у вигляді (х; у). Як можна зобразити ці пари чисел?
, де -1 ≤ х ≤ 4. Знайдіть пари значень х та у для всіх цілих значень х та запишіть їх у вигляді (х; у). Як можна зобразити ці пари чисел?
Виконайте відповідну побудову.


про публікацію авторської розробки
Додати розробку