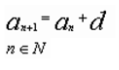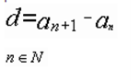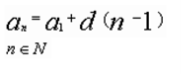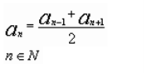Геметрична прогресія, її властивості. Формула н–го члена геометричної прогресії.

Геметрична прогресія, її властивості.
Формула  н–го члена геометричної прогресії.

Тип уроку: засвоєння нових знань і первинне закріплення.

Мета уроку: Формування поняття геометричній прогресії через поняття арифметичної прогресії, використовуючи методи зіставлення і протиставлення. Познайомити з властивостями геометричній прогресії і формулою n-го члена. Закріпити отримані знання на прикладах розв'язання задач.

Розвивати спостережливысь, вміння аналізувати, застосовувати прийоми порівняння, перенесення знань у нову ситуацію.

Виховувати пізнавальну активність, самостійність, прагнення розширювати свій кругозір.

Хід уроку

1. Організаційний момент.

Вчитель математики:

Прогрес – це рух, це велич, це зростання,

Як Україні зараз він потрібний,

Прогресії – його сестриці рідні.

Це школа, математика, навчання.

І кожен з нас, як аксіому знає:

Без математики на ноги нам не стати

Тож хай лунає лозунг наш крилатий

Прогресу без прогресій не буває!

Сьогодні на уроці ми з вами продовжимо працювати з прогресіями і введемо нові поняття. Виявляється прогресія може бути не тільки арифметичною, але мати й інший різновид.

А поки перевіримо домашнє завдання.

На столах у вас лежать картки

2. Перевірка домашнього завдання .

Самостійна робота з перевіркою в класі.

Для перевірки домашнього завдання, я пропоную написати невелику самостійну роботу. Прошу вас сісти по одному, взяти умову роботи. Самостійну роботу ви виконуєте на листочках. Час на виконання роботи 5 хвилин.   Потім перевіряємо відповіді та виставляємо оцінки в листок самооцінення. На рішення самостійної роботи відводиться 8 хвилин, на 9-ій хвилині переносимо відповіді в зошит.

(На екран виводиться текст самостійної роботи. Учитель прочитує завдання.)

Самостійна робота:

1. Запиши  перший  член і різницю арифметичної прогресії:
   1) 2; 7; 12; ...; 2) 6; 5,5; 5; ...; 3) 0,7; 1; 1,3; ...;  4) -9; -7; -5; ...
2. Знайдіть перші чотири члени арифметичної прогресії (а_п), у якої:

1) a₁ = 5, d = 2; 2) a₁ = 7, d = -2.

3. Знайдіть тридцять другий член арифметичної прогресії, якщо перший член 65 і різниця -2.
4. Знайдіть суму семи перших членів арифметичної прогресії 8; 4; 0; ...
5. Продовжіть числову послідовність, записавши ще 2 члени: 1; 2; 4; ...

Відповіді:

1. a₁ = 2, d = 5; a₁ = 6, d = -0,5; a₁ = 0,7, d = 0,3; a₁ = -9, d = 2;
2. 5;7;9;11…, 7;5;3;1…
3. а₃₂ = 3
4. У даній прогресії  a₁ = 8, d = -4  => S₇= 28
5. 1;2;4;8;16;…

Вивчення нового матеріалу.

Зверніть увагу на п’яте завдання самостійної роботи. Яким чином ви продовжили послідовність? (Учні відповідають.)

Тобто кожен наступний член дорівнює добутку попереднього на деякий одне і те ж число. Така числова послідовність у математиці називається геометричною прогресією.

Легенда

З геометричною прогресією, яку отримали в першому столітті, пов'язана цікава легенда.

За переказами, шахи були винайдені в п'ятому столітті до нашої ери в Індії. Індуський цар був так захоплений грою, що вирішив віддячити винахідника шахів. Який, у свою чергу, попросив наступну нагороду: видати йому за першу клітку шахівниці одне пшеничне зерно, за другу клітку - 2 пшеничних зерна, за третю - 4, за четверту - 8 зерен, за п'яту - 16 зерен і т.д. до 64-ї клітини дошки, тобто за кожну наступну клітину дошки слід видавати в 2 рази більше, ніж за попередню. Цар був незадоволений проханням, т.к. вважав, що винахідник, просячи настільки мізерну нагороду, ображає його.

І тоді придворний математик став рахувати, скільки зерна має отримати винахідник. Для того щоб підрахувати величину нагороди, ми повинні скласти зерна, що лежать на всіх клітинах дошки, тобто знайти суму, яку бачите на екрані.

Коли підрахували суму зерен, то кількості виявилося дуже велике число.

Яке? Ви дізнаєтеся трохи пізніше, коли познайомитеся з формулою суми n перших членів геометричної прогресії.

Якщо б цареві вдалося засіяти пшеницею площу всієї поверхні Землі, враховуючи і моря, і океани, і гори, і пустині. І Арктику з Артанктидою, і одержати хороший урожай, то через років п’ять як він міг би розрахуватись.

Але такої кількості зерен немає ні в якого царя, і прохання винахідника виконати неможливо.

А сьогодні ми познайомимося з поняттям геометричній прогресії. Відкрийте зошити запишіть число і тему уроку.

(В цей час учитель роздає кожному заготовлену таблицю)

Тепер попрацюємо по таблиці.

Прочитайте визначення арифметичній прогресії (з'являється на слайді) і сформулюйте визначення геометричній прогресії. (Учні відповідають і по клацанню на слайді з'являється визначення геометричній прогресії.) А тепер запишемо в таблицю визначення геометричній прогресії.

Скажіть мені будь ласка, як ми називаємо те число на яке збільшується кожен наступний член арифметичної прогресії? (Учні відповідають)

Познайомимося з назвою числа q. Дивіться слайд.

Наступний пункт в таблиці: позначення, дивимося слайд і записуємо.

Які значення можуть приймати перший член і знаменник геометричній прогресії? (Учні відповідають) Дивимося слайд. Слайд

Давайте виведемо рекуррентную формулу? Слайд

(На слайді спочатку з'являється рекуррентная формула арифметичній прогресії. Учні називають рекуррентную формулу геометричній прогресії. І по клацанню на слайді з'являється ця формула.)

А як знайти знаменник геометричної прогресії? (Учні міркують.) Слайд

(На слайді спочатку з'являється як знайди d. Учні за аналогією здогадуються, як знайти q і на слайді з'являється формула).

Використовуючи рекуррентную формулу, можна отримати формулу n-го члена. Розглянемо геометричну прогресію зі знаменником q.

Запишемо формулу в таблицю.

Раніше бачили, що назва арифметичній прогресії пов'язана з особливою властивістю членів цієї прогресії. Назва геометричній прогресії також пов'язана з властивістю її членів.

Отже, квадрат будь-якого члена геометричної прогресії, починаючи з другого, дорівнює добутку двох сусідніх членів, дивимося на слайд. Знайдемо квадратний корінь з обох частин цієї рівності, одержимо що для будь-яких трьох послідовних членів геометричної прогресії виконується рівність на слайді. А число, яке вийшло в правій частині рівності називається середнім геометричним двох чисел. Отже, запишемо характеристичне властивість.

Геометрична прогресія застосовується в багатьох областях. Наприклад, в економіці (обчислення вкладу, покладеного під деякий відсоток), в біології (розмноження мікроорганізмів), в геометрії, у фізиці, хімії і т.д. Подивіться, як застосування геометричній прогресії в геометрії.

У правильний трикутник, вписаний другий трикутник так, що його вершинами є середини сторін першого. У другій трикутник таким же способом вписаний третій і т.д. Розглянемо довжини сторін цих трикутника. (Учні міркують і відповідають.) Так як сторона кожного нового трикутника є середньою лінією попереднього трикутника, то якщо сторона першого трикутника - а, другий - 1/2 а, третій - 1/4 а, четвертого - 1/8 а й т. д. Таким чином, довжини сторін утворюють геометричну прогресію зі знаменником - 1/2.

Переходимо до вирішення завдань.

Первинне застосування знань і вмінь.

1. Чому дорівнює перший член і знаменник геометричної про­гресії:

Усно:

a) 2, 8, 32, 128,...;   б) 1,

в) 7, 7, 7, ...;  _Г) 3, , ...;

2. Запишіть перші п'ять членів геометричної прогресії, якщо:
   а) b₁ = 2, q = 3; б) b₁ = 4, q = -2;

в) b_l = 4, q = ;

3.  Знайдіть п'ятий член і знаменник геометричної прогресії, якщо;

а)b₄= ,  b₆= 81;           б) b₄=,  b₆ = 81;

в) b₄ - 9, b₆  = 3;                г) b₄ =, b₆ = .

4. Між наведеними парами чисел вставте додатне число так, щоб утворилось три послідовні члени геометричної прогресії:

а) 4 і 9;                      б) 3 і 4;                     в) і .

 

I. (Фізика) Мається радіоактивна речовина масою 256г, маса якого за добу зменшується вдвічі. Яка стане маса речовини на другу добу? На третій? На п'ятому? (256; 128; 64; 32; 16; ...)

II (Економіка) Строковий вклад, покладений в ощадний банк, щорічно збільшується на 5%. Яким стане вклад через 5 років, якщо спочатку він дорівнював 1000р.? (1000; 1050; 1102,5; 1157,625; 1215,5025; ...)

III. (Біологія) Бактерія за 1 секунду ділиться на три. Скільки бактерій буде в пробірці через 5 секунд? (1; 3; 9; 27; 81; ...)

 

Підсумок уроку

Давайте подивимося на таблицю, яку заповнювали під час пояснення нового матеріалу. Назвіть спільне та відмінне у визначенні та властивості арифметичної і геометричної прогресії? Де застосовується геометрична прогресія?

(Учні відповідають. Та аналізують сій листок самооцінки)

Домашнє завдання:

 

 

 

 

 

 

 

 

 

 

 

Додаток 1

 

Прогресія	Арифметична прогресія	Геометрична прогресія
Означення	Числова послідовність, кожен член якої, починаючи з другого дорівнює попередньому члену, до якого додається одне й те саме число .	Числова послідовність відмінних від нуля чисел, кожен член якої, починаючи з другого дорівнює попередньому члену, помноженому на одне й те саме число .
Позначається
Допустимі значення	Любі числа	Любі числа, окрім нуля
Рекурентна формула
Знаходження
Формула п – го члена
Властивості прогресії

 

 

 

 

 

 

 

 

 

 

Додаток 2

 

Прізвище________________________	1	2	3
Тестування (максимум 3 бали, одне завдання 0,5 бала)
Відповіді під час опитування (максимум 3 бали)
Оцініть свою участь у роботі групи під час опрацювання схеми (максимум 3 бали)
Оцініть свою участь у роботі малої групи під час розв’язування прикладу (максимум 3 бали)
Усього