Контроль знань по темі

«Логарифми»

(профільний рівень)

Чи знаєш ти логарифми?

Бліц-тест на знання властивостей.

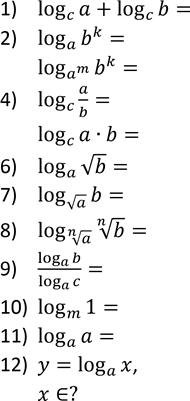3)

5)

∈?                

∈?

Тест

по темі «Логарифми»

(1-й рівень складності)

№1. Обчислити:

          а) 10            + 5 + 2

          б) log 9  

№2. Порівняти:

          а) log     3 і log

          б) log   2 і log   3  (в залежності від а).

№3. Дано: log 2 =    . Знайти: log   2 + log   5.

№4. Розташувати за зростанням: log   4; log     ; ln4; lg1.

№5. Розв`язати рівняння: 

          а) log (    + 1) = 2;

          б)            + ln    = 0.

№6. Розв`язати нерівності:

          а) lg(    − 2) ≥ 1;

          б) log       ≤ 2;

          в) (    − 6) ∙ log (    − 3) ≥ 0.

№7. Дано: lg 2 =    , lg 7 =   . Знайти: lg 56.

Відповіді:

№1. a) 4; б) 2

№2. а) “=”; б) при а>1 знак “<”; при 0<a<1 знак “>”

№3. −    −  

№4. log    ; lg 1 ; log  4 ; ln 4

№5. а) 15; б) 1;       

№6. а) [12; ∞); б) (0; 25]; в) (3; 4]∪[6; ∞)

№7. 3a+b

Тест

по темі «Логарифми»

(2-й рівень складності)

№1. Обчислити: log log     81.

№2. Які з чисел: а=       належать до проміжку (0; 1)?

№3. log   − log   + log   − log   =?

∙

                     =?

№5. Дано: log     27 = а. Знайти: log   16.

№6. Знайти область визначення: .

№7. Задано функції: ( ) = log (2 −           ); ( ) =          ; ℎ( ) =     − 2.

Серед наведених нерівностей виберіть ту, яка справедлива для всіх ∈ (−∞; 1]:

1)          ( ) <        ( ) < ℎ( );

2)          ℎ( ) <      ( ) < ( );

3)          ( ) < ℎ( ) <      ( ); 4) ℎ( ) <       ( ) < ( ).

№8. Дано функцію: ( ) = 1 − log (2 −         ). Знайдіть функцію ( ), яка є оберненою до даної на її області визначення. У відповідь запишіть значення (−1).

№9. Розв`яжіть рівняння:   .

№10. Скільки цілих розв`язків має нерівність:  < 1?

№11. Область визначення функції      =      log(  + 2) − log(1 −  ) є деяким числовим проміжком. Запишіть його довжину.

№12.              < 4 ∙             − 3.

Відповіді:

№1. 8

№2. a і d

№3. -6

№4. 2

(             ) №5.  

№6. (0,1)∪(1,5]

№7. 4)

№8. -7

№9. 0,01; 100

№10. 4

№11. 1,5

№12. ( , 1) ∪ (1,3)

Контрольна робота

«Логарифмічні рівняння»

Варіант I 

                  =

№2. О.Д.З.

№3. log      (3      − 12) = 2

№4. log      + 2 log      = 5

Варіант II 

№2. О.Д.З.

№3. log        + log      + log       = 7

№4.              = 100

Варіант III

№1. − log_√ + log      

№2. О.Д.З.

             = log   

№4. 3          +              = 54

Варіант IV

№2. О.Д.З.

             = log       

                                                  (          )

№3.      ^,               = 0,01    

№4. log (     − 1)    − log _, (

Відповіді:

Варіант I

№2. ∅

№3. 4

№4. 9

Варіант II

№1. -1

№2. [4; 2)∪(2; 3)

№3. 16

− 1) = 5

№4. 0,1; 100

Варіант III

№1.      

№2. (0; 1)∪(1; 2)

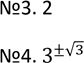
Варіант IV

№1. 7

№2. (0; 3)∪(3; 4)∪(4; 5)

№3. 100

Контрольна робота

«Логарифмічні нерівності»

Варіант I 

№1. log (       − 4    + 3) < 1

№2. log   log   > −1

№3. log (      + 2) ≥ log (− )

№4. 9          < 4            − 3

№5. log (3     − 1) > 1

Варіант II

№1. lg(−8 ) < lg        №2. log( − 2 ) ≥ −1

(      ) №3.  < 0

                         (          )

№4. log   log    log    ≤ 1

№5. log (       + 1) ≤ log (2 − 5 )

Варіант III

№1. log (        + 3 ) ≤ 2

№2. log        _, 2 < log    4

№3. log log    log (    − 1) > 0

№4.          ≤ 10000

№5. log   > 1

Варіант IV

№1. log _, (        − 2    − 3) ≥ −1

№2.          + 7       < 98

№3. > 400

№4. log   log log       > 0

№5. log    (    + 3) < 2

Відповіді:

Варіант I

№1. (-1; 1)∪(3; 5)

№3. [-1; 0)

№4. ( ; 1) ∪ (1; 3)

Варіант II

№3. (3; 4)

№4. [ ;   ]

№5. [ ; )

Варіант III

№3. (10; 82)

№4. [0,01; 100]

№5. (1; 3)

Варіант IV

№2. (0; 100)

№3. (20; 100)