Геометричні та алгебраїчні методи розвязування планіметричних задач

Суть синтетичного методу полягає в тому, що, виходячи з умови задачі чи теореми і використовуючи відомі твердження, будується ланцюг логічних міркувань, останнє з яких збігається з вимогою задачі. Наведемо приклад.

Суть аналітичного методу полягає в тому, що, виходячи з вимоги (висновку) твердження (теореми чи задачі) і спираючись на відомі твердження, будуємо ланцюг логічних міркувань, який показує, що вимога є наслідком умови. Наведемо приклад.

Суть методу від супротивного полягає в тому, що, маючи твердження, будуємо нове, заперечивши висновок попереднього. Утворюється протилежне твердження. Виходячи з висновку протилежного твердження, будуємо «ланцюг» істинних тверджень, поки не отримаємо твердження, яке суперечить або умові, або відомій аксіомі чи теоремі, або припущенню. Отже, отримуємо висновок, що протилежне твердження хибне, а тому початкове – істинне (тут діє логічний закон: з двох протилежних тверджень одне істинне, друге хибне, третього не дано). Розглянемо приклад.

Математичну задачу вважають розв’язаною, якщо: 1) записано відповідь у вигляді числа, виразу, вказано алгоритм побудови рисунка, коли це задача на обчислення, побудову чи дослідження; 2) підтверджено сформульоване в задачі твердження, коли це задача на доведення.

Метод від супротивного називають непрямим методом розв’язування математичних задач.

Розглянемо деякі інші методи розв’язування геометричних задач, які поділяють на види за використанням математичного апарату.

Алгебраїчний метод розв’язування задач

Розв’язуючи задачу алгебраїчним методом, слід приділити увагу таким етапам:

1. Моделювання тексту задачі за допомогою рисунка (у більшості випадків).

2. Введення позначень шуканих величин або тих, які приводять до шуканих (найчастіше літерами латинського алфавіту).

3. Складання рівняння або системи рівнянь, використовуючи введені позначення та відомі геометричні співвідношення між шуканими і даними величинами.

4. Розв’язування складеного рівняння або системи рівнянь.

Повернення до введених позначень і визначення шуканих геометричних величин. За потреби, виконання дослідження знайдених розв’язків.

5. Записування відповіді.

Вам доводилося неодноразово розв’язувати геометричні задачі алгебраїчними методами. Задачі, у яких задано залежність між двома вимірами, зводяться до розв’язування рівняння. Наприклад, одна зі сторін паралелограма на 3 см довша за іншу, а периметр – 30 см. Потрібно знайти довжини сторін паралелограма. Тоді, увівши змінну х як довжину сторони цього паралелограма, маємо довжину другої сторони (х – 3). Враховуючи означення периметра паралелограма та відоме його значення, отримуємо рівняння:

(x + x – 3) * 2 = 30.

Наведемо ще приклади розв’язування задач алгебраїчним методом.

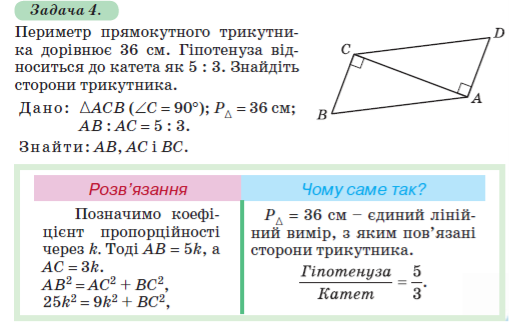
Метод площ

Якщо умова задачі містить дані, з яких легко знайти площу одним зі способів, однак, використовуючи інший спосіб для відшукання площі цієї самої фігури, маємо один з лінійних вимірів невідомий, то, прирівнюючи площі, отримують рівняння з одним невідомим.

Метод векторів

Щоб застосовувати метод векторів до розв’язування задачі, потрібно виконати такі дії:

1. Перевести задачу на мову векторів, тобто розглянути деякі дані в задачі відрізки як вектори та скласти векторну рівність.

2. Здійснити перетворення для векторної рівності, користуючися відповідними властивостями дій над векторами та відомими векторними рівностями.

3. Повернутися від векторної мови до геометричної.

4. Записати відповідь.

Метод векторів найчастіше використовується під час розв’язування задач, у яких вимагається довести: паралельність прямих (відрізків), поділ відрізка в певному відношенні; що три точки лежать на одній прямій; що даний чотирикутник – паралелограм (ромб, прямокутник, квадрат, трапеція). Проілюструємо суть цього методу на прикладі розв’язування задачі.

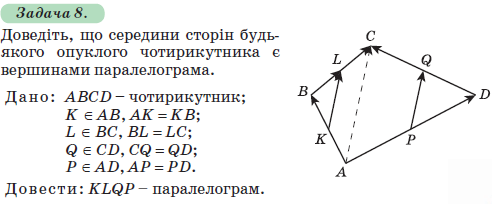
Метод координат

Розв’язуючи задачу координатним методом, слід виконати такі дії:

1. Записати геометричну задачу мовою координат.

2. Перетворити вираз чи обчислити його значення.

3. Перевести знайдений результат на мову геометрії.

4. Записати відповідь.

Методом координат найчастіше розв’язують задачі:

– на відшукання геометричних місць точок;

– на доведення залежностей між лінійними елементами геометричних фігур.

Розв’язуючи задачу методом координат, потрібно раціонально вибрати систему координат: дану фігуру слід розмістити відносно осей координат так, 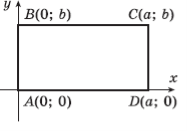щоб якнайбільше координат потрібних точок дорівнювало нулю, а також одному і тому самому числу. Наприклад, координати вершин прямокутника ABCD можна вибрати так, як на рисунку:

Проілюструємо суть методу на прикладі.

Метод геометричних перетворень: метод повороту, метод симетрії, метод паралельного перенесення, метод гомотетії.

Розв’язуючи задачі методом геометричних перетворень, розглядають поряд з даними фігурами нові фігури, які отримали з даних за допомогою певного перетворення. З’ясовують властивості нових фігур, переносять ці властивості на дані фігури, а далі – знаходять спосіб розв’язування задачі.

Кажуть, що задачі, які розв’язані методом векторів, методом координат, методом геометричних переміщень, методом площ та іншими методами, у яких використовується більше властивостей геометричних фігур, розв’язані геометричними методами.