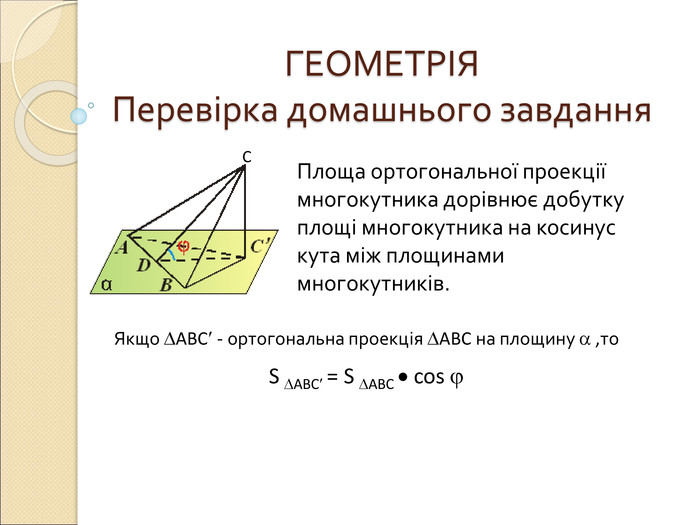
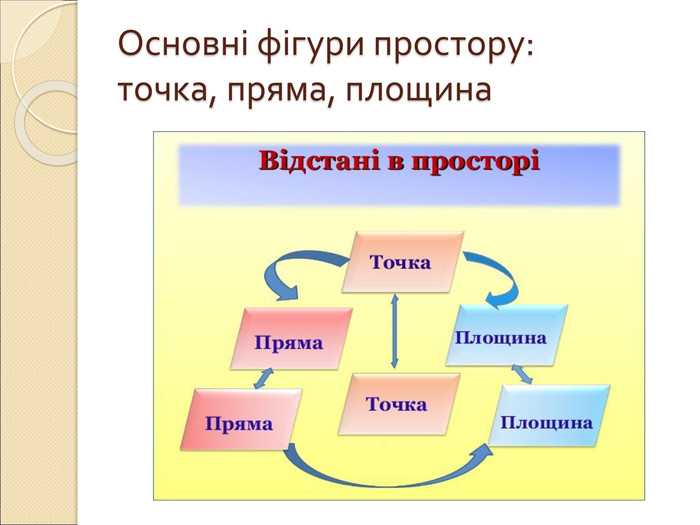
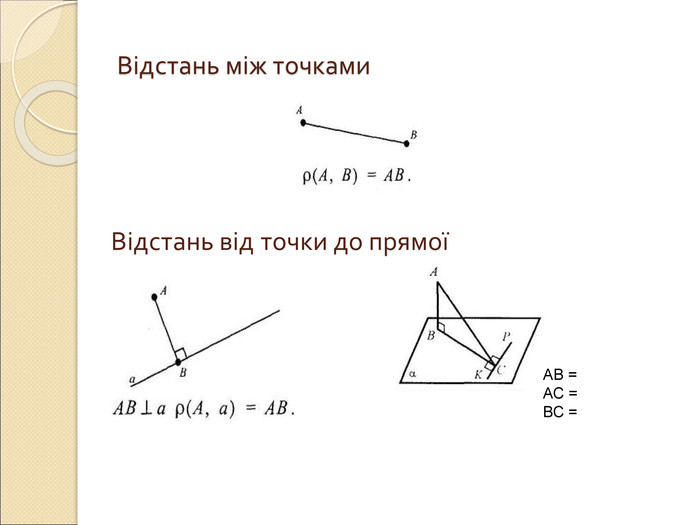
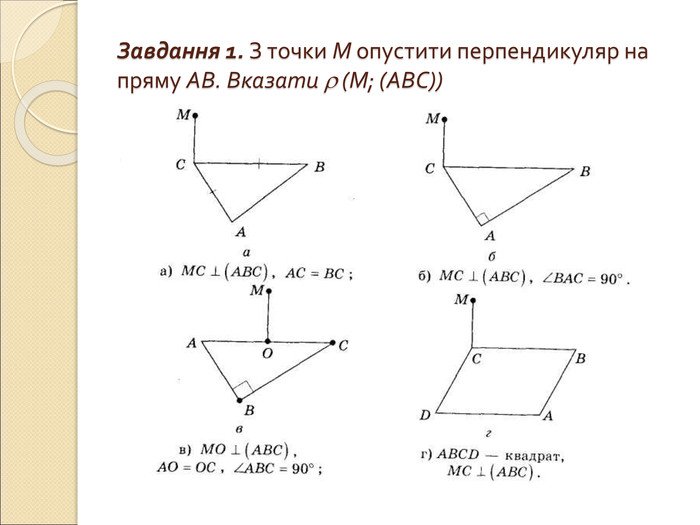
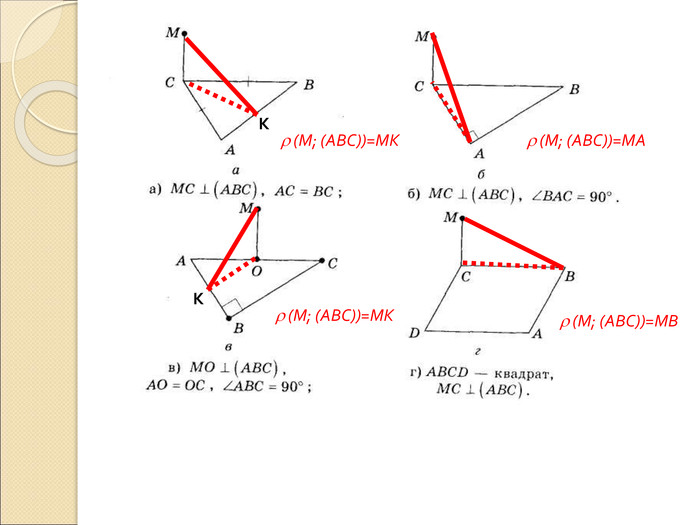
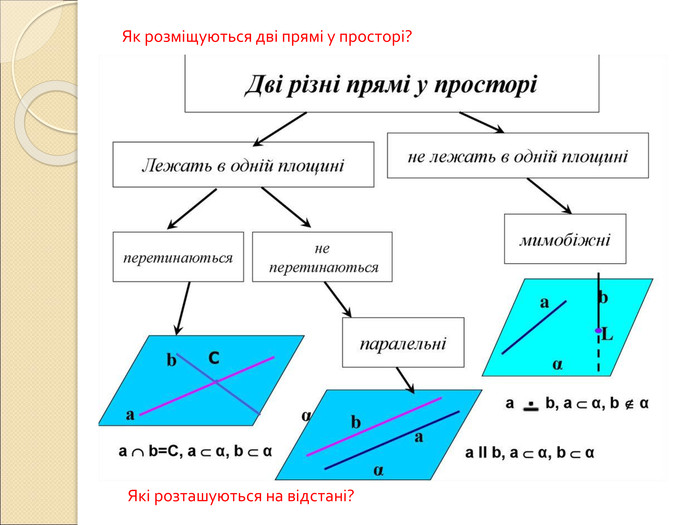
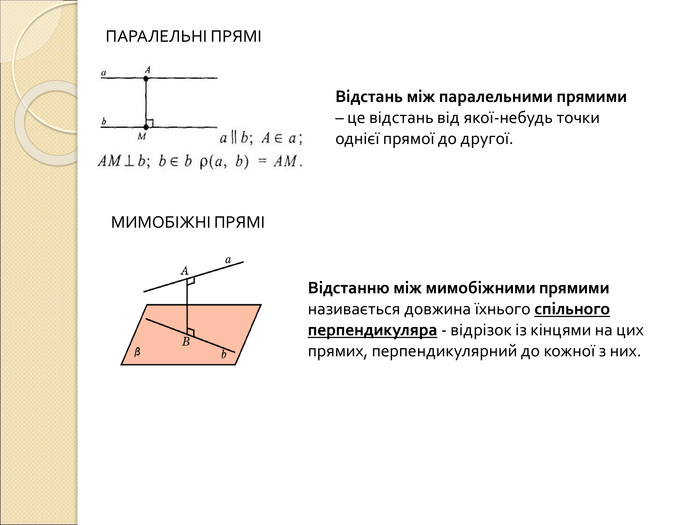
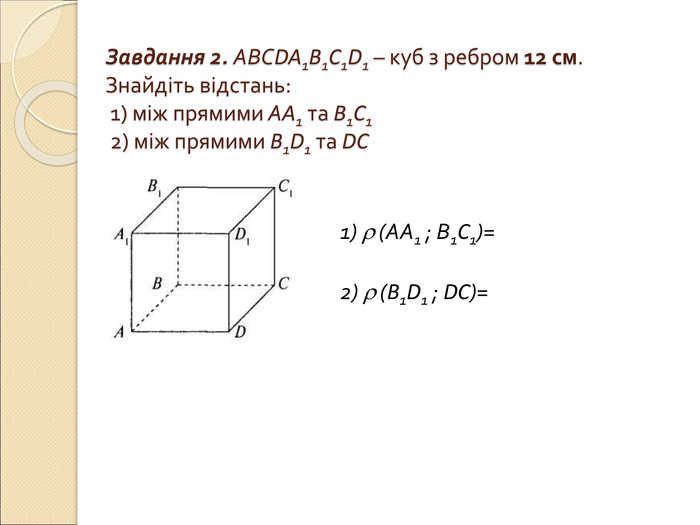
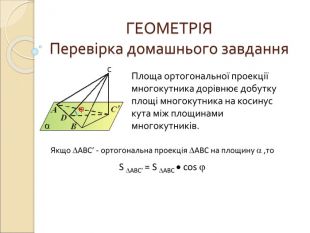
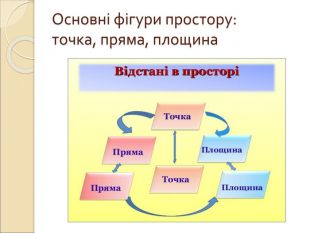
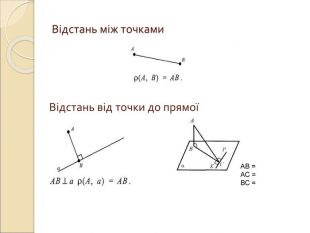
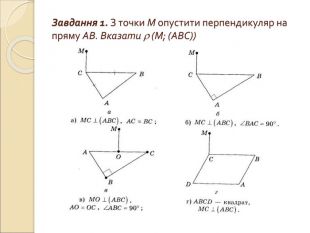
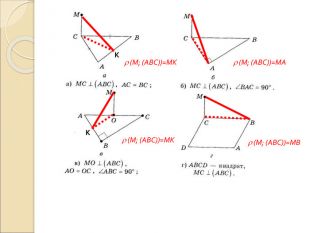
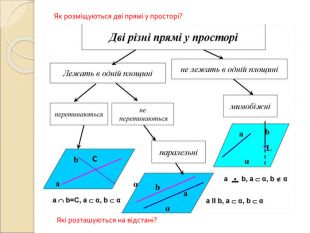
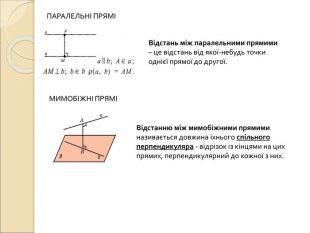
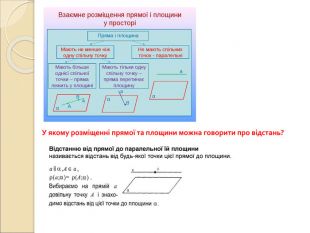
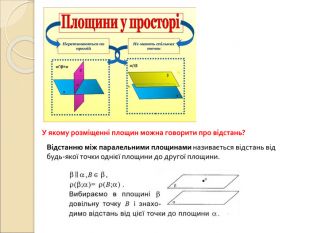
Презентація "Вимірювання відстаней у просторі"
Про матеріал
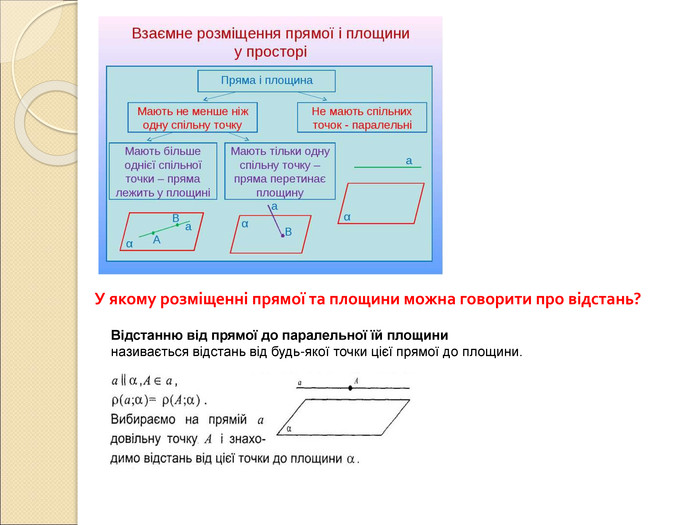
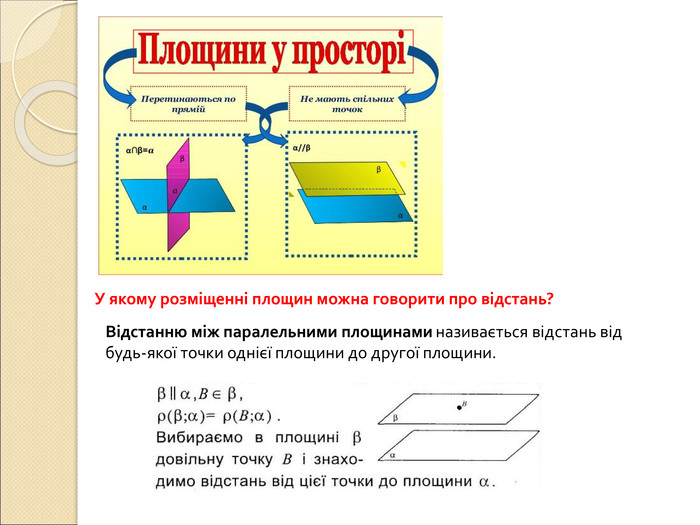
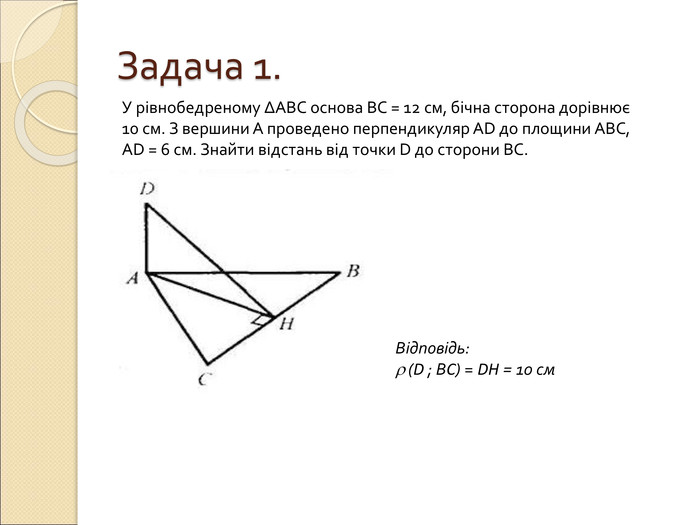
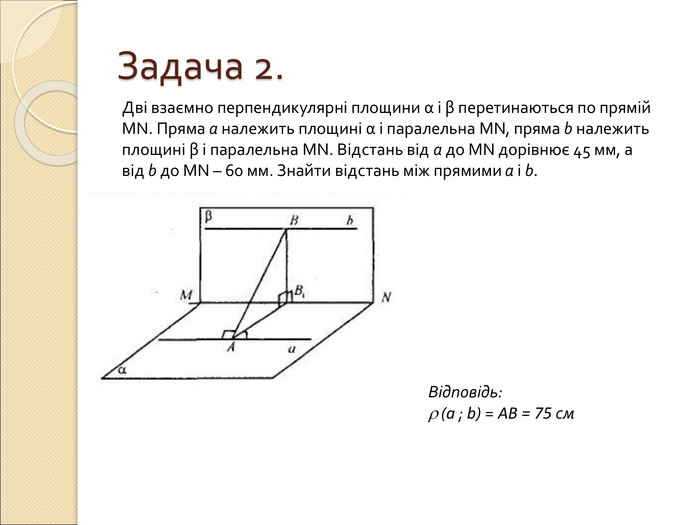
Презентація по темі "Вимірювання відстаней у просторі": пояснення нового матеріалу, диференційовані завдання, відповіді. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
Дякую, класна робота
-
ppt
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку