Геометрія. 11 клас. Площа бічної поверхні. Розв’язування задач.

 

 

 

 

 

 

План-конспект уроку геометрії

для 11 класу на тему:

“Площа бічної поверхні.

Розв’язування задач”

вчителя математики

Новгород-Сіверської державної

гімназії імені К.Д. Ушинського

Заєць Наталії Григорівни

 

 

 

 

 

 

 

 Тема: Площа бічної поверхні. Розв’язування задач.

Мета: 1) навчальна: закріпити знання учнів з теми “Піраміда”; вдосконалити вміння розв’язувати задачі та вміння застосовувати свої знання на практиці;

           2) виховна: виховувати дисциплінованість, уважність, охайність;

           3) розвиваюча: розвивати логічне мислення учнів, інтерес до навчання, якості колективізму, сприяти розвитку вміння послідовно і чітко висловлювати власні думки.

Тип уроку: урок закріплення знань, умінь і навичок.

 

№ п/п	Етапи уроку	Час	ОМВ
1.	Організаційна частина	1 – 2 хв.
2.	Оголошення теми, мети уроку	1 – 2 хв.	пояснення
3.	Актуалізація опорних знань	5 – 6 хв.	гра
4.	Розв’язування задач	30 – 35 хв.	гра
5.	Підведення підсумків	3 – 4 хв.	бесіда
6.	Домашнє завдання	1 – 2 хв.

 

Хід уроку

 

1. Організаційна частина.

Привітання вчителя з учнями. Перевірка присутніх.

2. Оголошення теми, мети уроку.

На сьогоднішньому уроці ми будемо розв’язувати задачі. Але не в звичній для нас формі, а в формі гри “ГОТ” – “Геометрично організоване товариство”. Чи заробляли ви коли- небудь власними знаннями гроші? А от сьогодні спробуєте заробити і купити на свою зарплатню собі оцінку. Зараз поділимось на дві групи – дві фірми. Вам потрібно придумати назву фірми і обрати собі директора. Кожній фірмі пропонується виконати певне завдання, що матеріально оцінюється. Наприкінці уроку будемо за результатами визначати не лише найуспішніше товариство, а й найкращих працівників. Зарплату працівникам згідно з їхнім вкладом в роботу фірми видає директор. Отже, починаємо гру.

3. Актуалізація опорних знань.

Фірмам по черзі пропонується відповісти на запитання, що важливі для їхньої успішної діяльності. Кожна правильна відповідь оцінюється в 100 $.

Торг І. “Теоретик”

1. Що таке піраміда?
2. Скільки бічних граней має n- кутна піраміда?
3. Що лежить в основі піраміди?
4. Що вам відомо про вершину і бічні ребра піраміди?
5. Як побудувати висоту піраміди?
6. Яка послідовність побудови піраміди?
7. Що є перерізами піраміди, які проходять через її вершини?
8. Як отримують зрізану піраміду?
9. Що є бічними гранями зрізаної піраміди?
10. Як побудувати зрізану піраміду?
11. Що ви знаєте про правильну піраміду?
12. Яку особливість має висота правильної піраміди?
13. Що є бічними гранями правильної піраміди (і зрізаної правильної)?
14. Що таке апофема?
15. Як знайти бічну поверхню правильної піраміди?
16. Як знайти бічну поверхню правильної зрізаної піраміди?

4. Розв’язування задач.

Торг ІІ “Мисливці за розумом”

Командам даються для розв’язання наступні задачі (час – 20-25 хв.).

І фірма

1. Знайдіть двогранні кути при основі правильної трикутної піраміди, площа основи якої дорівнює Q, а бічна поверхня – S. (500$).

2. Знайдіть сторону основи та апофему правильної чотирикутної піраміди, якщо її бічне ребро дорівнює 10 см, а бічна поверхня – 144 см2. (500$).

3. У правильній чотирикутній піраміді знайти сторону основи, якщо бічне ребро дорівнює 5 см, а повна поверхня 16 см2. (500$).

4. За даною стороною a і бічним ребром b знайдіть висоту правильної трикутної піраміди. (500$).

5. За даною стороною основи а і висотою b знайдіть апофему правильної чотирикутної піраміди. (500$).

ІІ фірма

1. Знайдіть двогранні кути при основі правильної чотирикутної піраміди, площа основи якої дорівнює Q, а бічна поверхня – S. (500$).

2. Знайдіть сторону основи та апофему правильної трикутної піраміди, якщо її бічне ребро дорівнює 10 см, а бічна поверхня – 144 см2. (500$).

3. У правильній чотирикутній піраміді знайти сторону основи, якщо бічне ребро дорівнює 10 см, а повна поверхня 36 см2. (500$).

4. За даною стороною a і бічним ребром b знайдіть висоту правильної чотирикутної піраміди. (500$).

5. За даною стороною основи а і висотою b знайдіть апофему правильної трикутної піраміди. (500$).

Торг ІІІ “Експериментатори”

Кожній команді дається набір правильних  фігур (шаблони) – 3- кутник, 4- кутник, 6-кутник. На кожній з цих правильних фігур зазначена довжина висоти піраміди. Необхідно виміряти лінійкою довжину сторони основи і обчислити S повне.

Набори фігур

І фірма

 

 

 

 

 

 

 

 

 

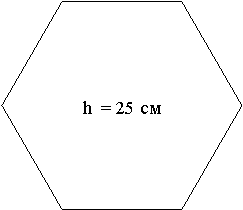
Зрізана піраміда

 

 

 

 

 

 

 

 

 

 

 

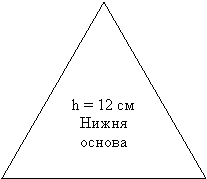
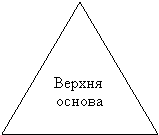
ІІ фірма

 

 

 

 

 

 

 

 

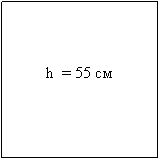
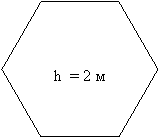
Зрізана піраміда

 

 

 

 

 

 

 

 

 

 

 

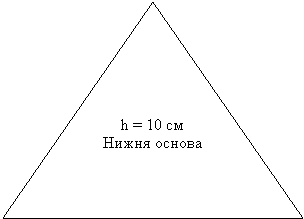
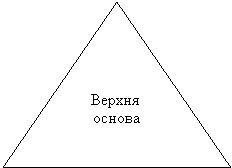
На виконання завдання дається 10 хв. Вартість кожного виконаного завдання становить по 500 $.

5. Підведення підсумків.

Вчитель визначає найкращу фірму і найактивнішого працівника та продає оцінки .

6. Домашнє завдання.

Погорєлов О. В. № 63, 69, 72.