Гра "Математичний футбол"

Математичний футбол

Правила гри

1. У грі беруть участь 2 команди. Кожна команда складається з воротаря, захисників і нападників.

2. Для вирішення завдання приймається тільки відповідь, без пояснень.

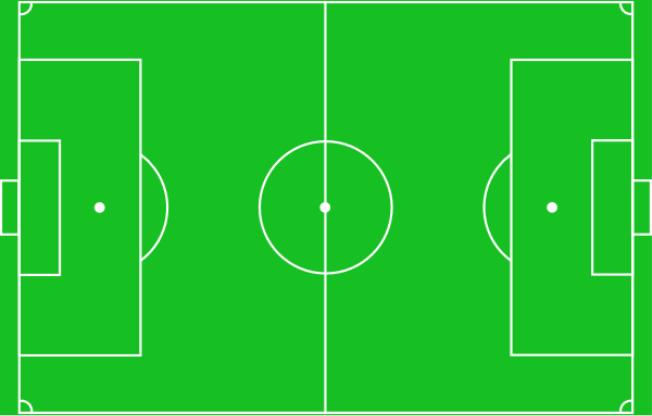
3. Поле ділиться на п'ять зон:

• центральна зона - для вкидання м'яча.

• дві зони захисту, де грають захисники однієї команди і нападники іншої.

• 2 воротарські зони, де грає один воротар і нападники протилежної команди.

4. На початку гри відбувається «вкидання м'яча». Всі члени команди повинні сидіти на місцях, читається умова задачі. Як тільки хтось розв’язує, він піднімає руку і з дозволу ведучого каже відповідь. Неправильна відповідь однієї команди рівносильна тому, що правильну відповідь дала інша команда. Якщо команда дала правильну відповідь, то до дошки виходять нападники цієї команди і захисники іншої. Тепер відповідь давати можуть тільки ті, хто грає біля дошки. Читається наступне завдання. Якщо перемагають нападники, то м'яч переходить у воротарську зону, і замість захисників другої команди виходить воротар. Якщо перемагають захисники, то м'яч переходить в зону захисту суперників, і команди міняються ролями: замість захисників виходять нападники, замість нападників захисники. Якщо у воротарській зоні воротар дає неправильну відповідь, або правильну відповідь дають нападники, то атакуюча команда забила гол. М'яч переміщається в центральну зону, відбувається вкидання. В іншому випадку м'яч переміщається в зону захисту команди, що обороняється, і замість воротаря знову виходять захисники.

5. За порушення дисципліни команда карається пенальті: воротар провинилася команди грає проти одного з гравців іншої команди за тими ж правилами, за якими зазвичай відбувається гра у воротарському зоні.

Завдання

1-ша команда

1. Операція, обернена до операції множення.

(Ділення)

2. Числа, які використовуються для лічби.

(Натуральні)

3. Число, що дорівнює відношенню довжини кола до довжини його діаметра.

(Пі)

4. Натуральне число Р > 1, натуральні дільники якого це тільки 1 та Р.

(Просте)

5. Чому дорівнює 1 пуд?

(16кг)

6. Рівняння, що мають одну і ту саму множину розв'язків.

(Рівносильні)

7. Наука про числа, їх властивості та дії над ними.

(Арифметика)

8. Як називається одна триста шістдесята части­на кола?

(Градус)

9. Одне яйце варять 4 хвилини, а скільки хвилин треба варити шість яєць?

(4 хвилини)

 

10. Скільки кілограмів в одному центнері?

(100кг)

11. Трійка коней пробігла 15 км. Скільки кіло­метрів пробіг кожен кінь?

(15км)

12. Скільки нулів у числі «мільйон»?

(6)

13. Сота частина числа.

(Відсоток)

14. Найбільша хорда у колі.

(Діаметр)

15. Яке натуральне число дорівнює кількості букв у його назві?

(Три)

16. Скільки разів на рік встає сонце?

(365)

 

2-га команда

1. Інша назва абсолютної величини числа.

(Модуль)

 

2. Наука про числа та операції над ними.

(Арифметика)

3. Два числа, добуток яких дорівнює одиниці.

(Взаємно обернені)

4. Прилад для вимірювання маси тіла.

(Терези)

5. Де записують знаменник дробу: над рискою чи під нею?

(Під нею)

6. Як називається шлях, пройдений тілом за оди­ницю часу?

(Швидкість)

7. Сума довільної кількості одночленів.

(Многочлен)

8. Одиниця маси коштовних каменів.

(Карат)

9. Пристрій для вимірювання кутів.

(Транспортир)

 

10. Горіло сім свічок, п'ять згасли. Скільки свічок залишилося?

(5,  решта згоріли)

11. Найбільше від'ємне число.

(-1)

12. Рівність двох відношень.

(Пропорція)

 

13. Чому дорівнює сума чисел від —5 до 5?

(0)

14. У батька п'ять дочок, і кожна дочка має бра­та. Скільки дітей у батька?

(Шестеро)

15. Чому дорівнює чверть години?

(15 хвилин)

16. Результат множення.

(Добуток)

Додаткові запитання

1. Сума років трьох братів дорівнює 21.  Чому вона буде дорівнювати через 6 років?

2. Замість того, щоб відняти 15, Петрик додав 15.  На скільки його результат відрізняється від правильного?

3. Яка остання цифра добутку 274 × 392 ×973?

4. Чи завжди правильна рівність а = а?

5. Скільки існує двозначних чисел?

6. Два батька й два сини з'їли на сніданок 3 яйця, причому кожен з'їв по одному. Як це могло статися?

7. Дівчинка має стільки ж братів, скільки й сестер, а в хлопчика

братів немає. Скільки в цій сім’ї хлопчиків і дівчаток?

8. Маємо два бідони на 4 і 5 літрів. Чи можна відміряти ними 3 літра води і як саме?

9. Зустрілись троє друзів і вирішили зіграти в шахи. Домовились, що кожен з кожним зіграє один раз. Скільки було зіграно партій?

10. Як записати число 100, використовуючи лише п’ять одиниць?

11. До міста їде мотоцикліст, а назустріч йому – 2 легкових, 3 вантажних автомобілі і 1 велосипедист. Скільки автомобілів їде до міста?

12. Два туристи пройшли за день 34 км. Скільки кілометрів пройшов кожний, якщо вони йшли з однаковою швидкістю?

13. Назвіть число, яке не впливає на суму і число, що не впливає на добуток.

14. Скільки буде, коли 10 поділимо на половину?

15. Знайдіть значення виразу

( 2389586 + 64472891)×(5657429 – 5657429) : 564832028

 

Поле для гри