Границя функції в точці
Тема уроку: Границя функції неперервного аргументу.
Мета уроку: Формування поняття про границю функції.
І. Перевірка домашнього завдання.
1. Перевірити наявність виконаних домашніх завдань та відповісти на запитання, що виникли в учнів при виконанні домашніх завдань.
2. Сформулюйте означення і властивості модуля дійсного числа, користуючись таблицею 1.
3. Усне розв'язування рівнянь і нерівностей з модулем за таблицею 2 для усних обчислень.
Таблиця 2
|
|
1 |
2 |
3 |
4 |
|
1 |
|х| = 5 |
|х| = 0 |
х = – 5 |
|х| = х |
|
2 |
|х| = – х |
|х – 3| = 2 |
|х + 2| = 3 |
|х – 1| + |х + 1| = 0 |
|
3 |
|х| < 2 |
|х| > 0 |
|х| > –1 |
|х| > 3 |
|
4 |
|х – 1| < 2 |
|х + 1| < 2 |
|х – 1| > 3 |
|х + 3| > 1 |
II. Сприймання поняття границі функції.
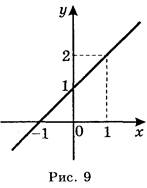
Побудуємо графік функції f(x) = х + 1 (рис. 9). Якщо х наближається до 1, то значення у наближається до 2.
Говорять, що границя функції f(x) при х, що наближається до 1, дорівнює 2 і записується: ![]() (x +1) = 2.
(x +1) = 2.
Розглянемо другий приклад.
Побудуємо графік функції g(x) = 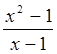 і розглянемо поведінку цієї функції при х, близьких до 1.
і розглянемо поведінку цієї функції при х, близьких до 1.
Функція g(x) = 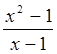 визначена при х
визначена при х ![]() (-
(-![]() ; 1)
; 1) ![]() (1; +
(1; +![]() ) і графік являє собою пряму у = х + 1 з виколотою точкою х = 1 (рис. 10), бо функція g(x) =
) і графік являє собою пряму у = х + 1 з виколотою точкою х = 1 (рис. 10), бо функція g(x) =
= 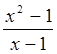 не визначена в точці х = 1.
не визначена в точці х = 1.
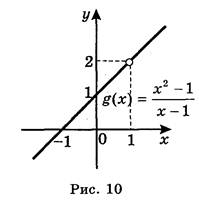 Якщо х наближається до 1 (зліва чи справа), то у наближається до 2 (відповідно знизу чи зверху).
Якщо х наближається до 1 (зліва чи справа), то у наближається до 2 (відповідно знизу чи зверху).
Отже, ![]()
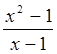 =2.
=2.
Розглянемо третій приклад. Побудуємо графік функції
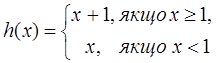 (рис. 11) і розглянемо поведінку функції при х, що наближається до 1.
(рис. 11) і розглянемо поведінку функції при х, що наближається до 1.
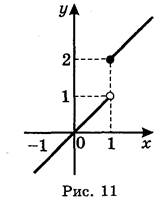 При х → 1 (що наближається до 1) границі функції h(x) не існує, поскільки не існує єдиного числа, до якого наближається функція при х, що прямує до 1.
При х → 1 (що наближається до 1) границі функції h(x) не існує, поскільки не існує єдиного числа, до якого наближається функція при х, що прямує до 1.
(Якщо х наближається до 1 зліва, то h(x) наближається до 1; якщо ж х наближається до 1 справа, то h(x) наближається до 2).
Таким чином:
Якщо при значеннях х, що прямують до деякого числа а, значення функції f(x) прямують до єдиного значення b, то говорять, що при х, що наближається до а, функція f(x) має границю, яка дорівнює b, і це записується так: ![]() f(x) = b або f(x) → b при х → а.
f(x) = b або f(x) → b при х → а.
ІІІ. Виконання вправ
1. Використовуючи графіки функцій (рис. 12), з'ясуйте:
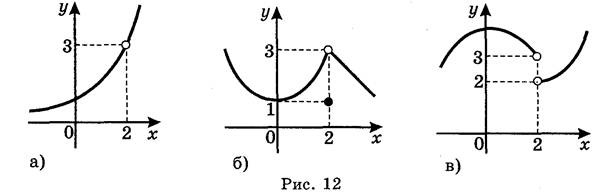
1) Чи має границю функція в точці х, що прямує до 2? Якщо має, то чому дорівнює ця границя?
2) Чи залежить існування границі функції в точці від визначеності функції в цій точці?
3) Якщо функція визначена в точці, то чи завжди границя функції дорівнює значенню функції в цій точці? 2. Користуючись графіком, знайти границі (якщо вони існують): a) ![]() б)
б) ![]() в)
в) 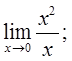 г)
г) 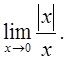
IV. Осмислення поняття границі функції.
Нехай задано деяку функцію, наприклад, f(x) = 2х + 1. Розглянемо таблицю значень цієї функції в точках, що досить близько розташовані до числа 1 (і в самій точці 1), та знайдемо |х – 1| та |f(x) – 3| у відповідних точках.
|
х |
0,5 |
0,8 |
0,9 |
0,99 |
0,999 |
1 |
1,001 |
1,01 |
1,1 |
1,5 |
|
f(x) |
2 |
2,6 |
2,8 |
2,98 |
2,998 |
3 |
3,002 |
3,02 |
3,2 |
4 |
|
|х – 1| |
0,5 |
0,2 |
0,1 |
0,01 |
0,001 |
0 |
0,001 |
0,01 |
0,1 |
0,5 |
|
|f(x) – 3| |
1 |
0,4 |
0,2 |
0,02 |
0,002 |
0 |
0,002 |
0,02 |
0,2 |
1 |
З таблиці видно, що при наближенні значення аргументу до числа 1 значення функції наближається до числа 3, при цьому похибка значень функції може бути досягнена як завгодно малою, шляхом зменшення похибки аргументу. Дійсно, взявши довільне ε > 0, тоді |f(x) – 3| < ε,
або |2х + 1 – 3| < ε; |2х – 2| < ε, 2|х – 1| < ε; |х – 1| < ![]() .
.
Отже, щоб похибка значень функції не перевищувала ε > 0, слід взяти значення х такі, що |х – 1| < ![]() .
.
Число b називається границею функції у = f(x) в точці а, якщо для будь-якого ε > 0 існує таке число δ = δ(ε) > 0, що для всіх х: 0 < |х – а| < δ, виконується нерівність |f(x) – b| < ε. (Рис. 13).
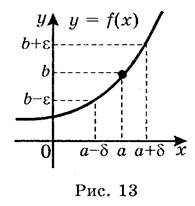 Розглянемо приклад.
Розглянемо приклад.
Доведіть, що ![]() (2x – 1) = 5.
(2x – 1) = 5.
Розв'язання Задамо довільне ε > 0 і покажемо, що існує δ > 0 таке, що із нерівності |х - 3| < δ випливає нерівність |(2х - 1) - 5| < ε. Маємо |(2х - 1) - 5| < є,
|2х - б| < ε; |2(х - 3)| < ε; 2·|х - 3| < ε; |х - 3| < ![]() Отже, якщо взяти δ =
Отже, якщо взяти δ = ![]() , то виконання нерівності
, то виконання нерівності
| x - 3| < δ приведе до виконання нерівності |(2x - 1) - 5| < ε. Отже, згідно з означенням границі маємо: ![]() (2x -1) = 5.
(2x -1) = 5.
Виконання вправи № 12 (3).
V. Домашнє завдання.
§ 33 Запитання і завдання для повторення № 6. Вправи № 2 (6), 12 (1).
Опрацювати конспект та виконати завдання в зошиті.
VІ. Підведення підсумків уроку.


про публікацію авторської розробки
Додати розробку
