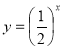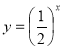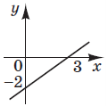III. Функції. Частина 4. Показникові та логарифмічні функції, їхні основні властивості

Про матеріал

Посібник призначений для підготовки учнів загальноосвітніх навчальних закладів та абітурієнтів до зовнішнього незалежного оцінювання з математики. Його укладено до чинної програми та чинних навчальних програм з математики. Метою посібника є надання практичної допомоги учням у підготовці до ЗНО та ДПА.

Перегляд файлу

Показникові та логарифмічні функції, їхні основні властивості.

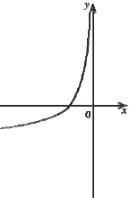
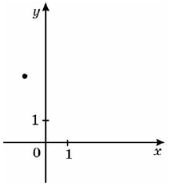
(2008)10. На рисунку зображено точку, через яку проходить графік функції . Укажіть функцію .

А	Б	В	Г	Д

Відповідь: Д.

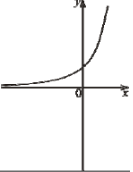
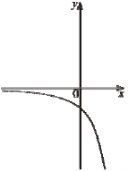
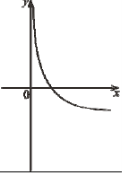
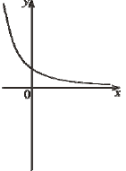
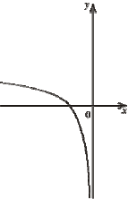
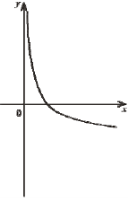
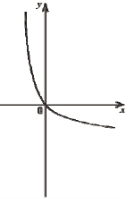
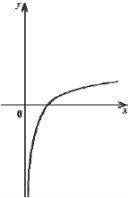
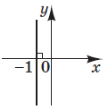
(2010)20. На одному з рисунків зображено ескіз графіка функції . Укажіть цей рисунок.

А	Б	В	Г	Д

Відповідь: Д.

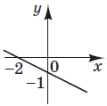
(2010)20. На одному з рисунків зображено ескіз графіка функції . Укажіть цей рисунок.

А	Б	В	Г	Д

Відповідь: Б.

(2012)5. Використовуючи зображені на рисунку графіки функцій, розв’яжіть нерівність .

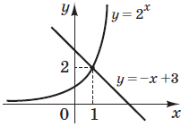
А	Б	В	Г	Д

Відповідь: Б.

(2012)7. Укажіть область визначення функції .

А	Б	В	Г	Д

Відповідь: Б.

(2014)23. Установіть відповідність між твердженням (1 – 4) та функцією (А – Д), для якої це твердження є правильним.

Твердження		Функція
1	графік функції проходить через точку	А
2	найменшого значення функція набуває в точці	Б
3	областю визначення функції є множина	В
4	графік функції симетричний відносно осі	Г
		Д

Відповідь: 1 – В; 2 – Б; 3 – А; 4 – Г.

(2015)23. До кожного початку речення (1 – 4) доберіть його закінчення (А – Д) так, щоб утворилося правильне твердження.

Початок речення		Закінчення речення
1	Функція	А	набуває від’ємного значення в точці
2	Функція	Б	не визначена в точці
3	Функція	В	має екстремум у точці
4	Функція	Г	набуває додатного значення в точці
		Д	є непарною

Відповідь: 1 – Д; 2 – В; 3 – А; 4 – Б.

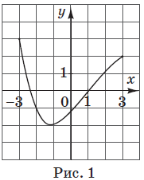
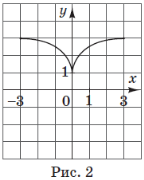
(2016)21. На рисунках (1 – 5) зображено графіки функцій, визначених на відрізку . До кожного запитання (1 – 4) доберіть правильну відповідь (А – Д).

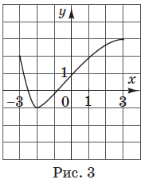
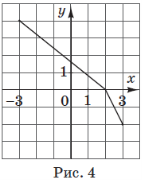
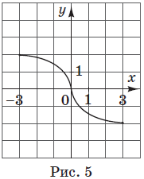
Запитання		Відповідь
1	На якому рисунку зображено графік функції, що проходить через точку ?	А	рис.
2	На якому рисунку зображено графік парної функції?	Б	рис.
3	На якому рисунку зображено графік функції, що має дві спільні точки з графіком функції ?	В	рис.
4	На якому рисунку зображено графік функції, що зростає на відрізку ?	Г	рис.
		Д	рис.

Відповідь: 1 – А; 2 – Б; 3 – Г; 4 – В.

(2016)21. На рисунку зображено графік функції , визначеної на відрізку . Установіть відповідність між функцією (1 – 4) та абсцисою (А – Д) точки перетину графіка цієї функції з графіком функції .

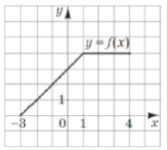
Функція		Абсциса точки перетину
1		А
2		Б
3		В
4		Г
		Д

Відповідь: 1 – Д; 2 – Г; 3 – Б; 4 – В.

(2016)31. Побудуйте графік функції . Користуючись графіком, визначте область значень цієї функції.

Відповідь: .

(2017)21. Установіть відповідність між функцією (1 – 4) та прямою, зображеною на рисунку (А – Д), яка не має з графіком цієї функції жодної спільної точки.

Функція		Графік функції
1		А
2		Б
3		В
4		Г
		Д

Відповідь: 1 – А; 2 – В; 3 – Г; 4 – Б.

(2018)21. До кожного початку речення (1 – 4) доберіть його закінчення (А – Д) так, щоб утворилося правильне твердження.

Початок речення		Закінчення речення
1	Пряма	А	є паралельною прямій .
2	Пряма	Б	не має спільних точок з графіком функції .
3	Пряма	В	перетинає графік функції у точці з абсцисою .
4	Пряма	Г	є паралельною осі .
		Д	є бісектрисою I і III координатних чвертей.