III. Функції. Частина 7. Дослідження функції за допомогою похідної. Побудова графіків функцій

Дослідження функції за допомогою похідної. Побудова графіків функцій.

(2006)29. Відрізок см завдовжки поділили на дві частини так, що сума площ квадратів, побудованих на цих частинах, стала найменшою. Обчисліть суму площ квадратів.

Відповідь: .

(2007)31. Знайдіть найбільше значення функції на проміжку .

Відповідь: .

(2008)36. Задано функцію .

1. Знайдіть проміжки зростання та спадання функції, екстремуми функції.

2. Побудуйте ескіз графіка функції .

3. Знайдіть кількість коренів рівняння , де , залежно від значення параметра .

У відповідь запишіть найбільше ціле , при якому рівняння не має коренів. Якщо такого значення не існує, у відповідь запишіть число .

Відповідь: .

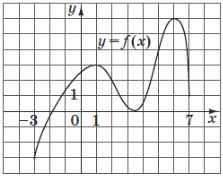
(2013)5. На рисунку зображено графік неперервної функції , визначеної на відрізку . Скільки всього точок екстремуму має ця функція на відрізку ?

Відповідь: В.

(2017)31. Задано функцію .

1. Визначте координати точок перетину графіка функції з осями координат.

2. Побудуйте графік функції .

3. Знайдіть похідну функції .

4. Визначте кутовий коефіцієнт дотичної, проведеної до графіка функції у точці з абсцисою .

Відповідь: 1. , , ; 3. ; 4. .