III. Функції. Частина 5. Тригонометричні функції, їхні основні властивості

Про матеріал

Посібник призначений для підготовки учнів загальноосвітніх навчальних закладів та абітурієнтів до зовнішнього незалежного оцінювання з математики. Його укладено до чинної програми та чинних навчальних програм з математики. Метою посібника є надання практичної допомоги учням у підготовці до ЗНО та ДПА.

Перегляд файлу

Тригонометричні функції, їхні основні властивості.

(2006)9. Знайдіть множину значень функції .

А	Б	В	Г	Д
				інша відповідь

Відповідь: Б.

(2007)10. Укажіть парну функцію.

А	Б	В	Г	Д

Відповідь: Д.

(2008)9. Укажіть найменший додатний період функції .

А	Б	В	Г	Д

Відповідь: В.

(2009)30. Знайдіть найбільше значення функції . Якщо функція не має найбільшого значення, то у відповідь запишіть число .

Відповідь: .

(2010)27. Установіть відповідність між функціями, заданими формулами (1 – 4), та їхніми властивостями (А – Д).

Функція	Властивість функції
1	А	областю визначення функції є проміжок
2	Б	функція спадає на інтервалі
3	В	функція зростає на інтервалі
4	Г	парна функція
	Д	періодична функція з найменшим додатним періодом

Відповідь: 1 – В; 2 – Г; 3 – Д; 4 – Б.

(2010)27. Установіть відповідність між функціями, заданими формулами (1 – 4), та їхніми властивостями (А – Д).

Функція	Властивість функції
1	А	областю визначення функції є інтервал
2	Б	областю значень функції є відрізок
3	В	функція спадає на інтервалі
4	Г	непарна функція
	Д	періодична функція, що не має найменшого додатного періоду

Відповідь: 1 – Б; 2 – Г; 3 – Д; 4 – В.

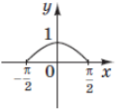
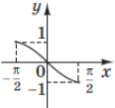
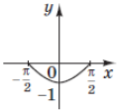
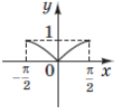
(2011)26. Установіть відповідність між функціями (1 – 4) та ескізами їхніх графіків (А – Д).

Функція		Ескіз графіка функції
1		А
2		Б
3		В
4		Г
		Д

Відповідь: 1 – Г; 2 – Б; 3 – Д; 4 – А.

(2012)22. Кожній точці (1 – 4) поставте у відповідність функцію (А – Д), графіку якої належить ця точка.

Точка		Функція
1		А
2		Б
3		В
4		Г
		Д

Відповідь: 1 – В; 2 – Г; 3 – А; 4 – Д.

(2013)14. Укажіть парну функцію.

А	Б	В	Г	Д

Відповідь: Д.

(2013)28. Знайдіть найменший додатний період функції .

Відповідь: .

(2013)28. Знайдіть найменший додатний період функції .

Відповідь: .

(2013)28. Знайдіть найменший додатний період функції .

Відповідь: .

(2013)22. Установіть відповідність між твердженням (1 – 4) та функцією (А – Д), для якої це твердження є правильним.

Твердження		Функція
1	графік функції не перетинає жодну з осей координат	А
2	областю значень функції є проміжок	Б
3	функція спадає на всій області визначення	В
4	на відрізку функція має два нулі	Г
		Д

Відповідь: 1 – В; 2 – Г; 3 – А; 4 – Б.

(2013)28. Знайдіть найбільше значення функції .

Відповідь: .

(2013)28. Знайдіть найбільше значення функції .

Відповідь: .

(2013)28. Знайдіть найбільше значення функції .

Відповідь: .

(2014)22. Установіть відповідність між функцією (1 – 4) та кількістю спільних точок (А – Д) графіка цієї функції з графіком функції .

Функція	Кількість спільних точок
1	А	жодної
2	Б	лише одна
3	В	лише дві
4	Г	лише три
	Д	більше трьох

Відповідь: 1 – Б; 2 – А; 3 – В; 4 – Г.

(2014)11. На якому з рисунків зображено фрагмент графіка функції на проміжку ?

А	Б	В	Г	Д

Відповідь: Б.

(2015)21. Установіть відповідність між функцією (1 – 4) та координатними чвертями (А – Д), у яких розміщений графік цієї функції (координатні чверті показано на рисунку).

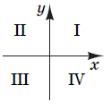
Функція	Координатні чверті
1	А	II та IV
2	Б	III та IV
3	В	I, II та III
4	Г	I, III та IV
	Д	I, II, III та IV

Відповідь: 1 – Б; 2 – В; 3 – А; 4 – Д.

(2015)13. На рисунку зображено фрагмент графіка однієї з наведених функцій на проміжку .

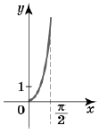
А	Б	В	Г	Д

Відповідь: Д.

(2016)5. Графіком однієї з наведених функцій є пряма. Укажіть цю функцію.

А	Б	В	Г	Д

Відповідь: Г.

(2016)18. Графік функції можна отримати внаслідок паралельного перенесення графіка функції уздовж осі .

А	Б	В	Г	Д
вправо на одиниць	вправо на одиниць	вправо на одиниць	вліво на одиниць	вліво на одиниць

Відповідь: А.

(2017)9. На рисунку зображено фрагмент графіка однієї з наведених функцій на проміжку . Укажіть цю функцію.

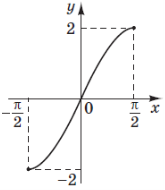
А	Б	В	Г	Д

Відповідь: А.

(2018)17. На рисунку зображено фрагмент графіка періодичної функції з періодом , яка визначена на множині дійсних чисел. Укажіть серед наведених точку, що належить цьому графіку.

А	Б	В	Г	Д

Відповідь: Д.

(2018)21. На рисунках (1 – 4) зображено графіки функцій, кожна з яких визначена на проміжку . Установіть відповідність між графіком функції (1 – 4) та властивістю (А – Д), що має ця функція.

Графік функції	Властивість функції
1	А	графік функції не перетинає графік функції
2	Б	графік функції є фрагментом графіка функції
3	В	множиною значень функції є проміжок
4	Г	функція спадає на проміжку
	Д	функція зростає на проміжку