ТЕМА УРОКУ: « АРИФМЕТИЧНА ПРОГРЕСІЯ , її властивості. Формула n – го члена арифметичної прогресії»

«Серед усіх наук, що відкривають людству шлях до пізнання законів природи, наймогутніша, найвеличніша наука – математика »

(С.В.Ковалевська.)

Підготувала :Гунько Любов Іванівна

Посада: вчитель математики

Місце роботи: Чернігівська ЗОШ 

I-IIIступенів №21 Формування компетентностей:

математична компетентність: домогтися засвоєння учнями: означення

арифметичної прогресії, відповідної термінології (різниця арифметичної прогресії); рекурентної формули та основних властивостей арифметичної прогресії (включаючи характеристичну властивість);виробити вміння: відтворювати зміст вивчених понять, а також використовувати їх для розв'язування задач, що передбачають виділення арифметичної прогресії серед інших числових послідовностей, використовувати рекурентну формулу арифметичної прогресії, та  властивості арифметичної прогресії; ключові компетентності:    інформаційно – числова компетентність: оперувати числовою інформацією,

діяти за алгоритмами; соціальна та громадянська компетентності: висловлювати власну думку, аргументовано відстоювати свої міркування, уміння спостерігати, помічати закономірності, проводити міркування за аналогією.

Тип уроку:  урок формування знань вмінь і навичок

Обладнання на уроці: комп'ютер,  мультимедійний проектор

Хід уроку

I.                  Організаційний етап

(На уроці працює 4 команди: «Теоретики», «Практики», «Дослідники», «Філософи»)

II.               Перевірка домашнього завдання  III. Формулювання мети і завдань уроку.

IV. Актуалізація опорних знань та вмінь учнів Команда «Теоретики»

1.    Що таке числова послідовність?

2.    Що називають членами числової послідовності?

3.    Які визнаєте способи задання числових послідовностей?

4.    Наведіть приклади задання числової послідовності формулою її загального член. 

5.    Кого із вчених називали “Королем математики”

          а) Ломоносова;    б) Гаусса;    

          в) Піфагора;         г) Галілея.

6.    Яка послідовність називається зростаючою(спадною)?

Команда «Практики»

Закінчити речення.

1.                     Послідовності бувають…………………………………………

2.                     Запишіть     формулу     для    послідовності       парних чисел:……………………………………………………………………

3.                     Запишіть     формулу     для    послідовності       непарних    чисел:

………………………………………………………………………………

4.                     Дано послідовність чисел:   4, 9, 14, 19, 24, 29, 34,…. Для четвертого члена даної послідовності запишіть: попередній член……………………. І наступний член………………………………………………………………………          .

5.                     Послідовність називають зростаючою, якщо

……………………………………………………………………………………  .

6.                     Послідовність називають спадною, якщо 

………………………………………………………………………………………………………………………     .

Команда « Дослідники»

1.                       Запишіть послідовність, яку утворюють шість перших непарних послідовних чисел.

2.                       Запишіть послідовність з семи чисел, перший член якої дорівнює 3, а кожен наступний на 4 більший за попередній.

3.                       Запишіть послідовність з восьми чисел, перший член якої дорівнює 8, а кожен наступний удвічі менший.

4.                       Запишіть послідовність з семи чисел, перший член якої 3, другий – 4, а кожен наступний дорівнює сумі двох попередніх. 5.       Продовжте ряд послідовних чисел  4, 8, 16, 32,…

6.         Запишіть перші сім натуральних членів послідовності, кожен з яких кратний 3.

V Мотивація навчання Команда «Філософи»

Із історії арифметичної прогресії

Прогресії як часткові види числових послідовностей, трапляються в папірусах ІІ тисячоліття до н. е. Перші із задач на прогресії, що дійшли до нас, пов’язані з господарською діяльністю, а саме – з розподілом продуктів, поділом спадку тощо.

Перші спогади про арифметичну прогресію були ще у прадавніх народів. У клинописних вавилонських табличках і єгипетських папірусах зустрічаються задачі на прогресії та вказівки як їх розв’язувати. 

 

 Вважалось, що в давньоєгипетському папірусі Ахмеса перебувала найдавніша задача на прогресії про поділ ячменю: 1) “Нехай тобі сказали: розділи десять мір ячменю між 10 чоловіками так, щоб різниця між кожним чоловіком і його сусідом становила 1/8 міри ячменю ”.

Ось одна з таких задач: 2) “10 братів; 1 2/3 міри срібла; брат над братом піднімається; на скільки піднімається, я не знаю. Частка восьмого 6 мехелів. Брат над братом на скільки піднімається? Яка частка кожного брата?”(1 2/3 міри становлять 100 мехелів). 

  Значна кількість задач на прогресії міститься  в чудовій пам’ятці математичної літератури початку XVIII cт. “Арифметиці” Л. П. Магніцького. Протягом півстоліття ця книга була основним математичним підручником в Росії. М.В. Ломоносов дуже високо цінив книгу Л.П. Магніцького, називаючи її “вратами ученості” .           

 

В цій книжці була ось така задача: 3)  „ Хтось продавав коня. Просив за нього 25 рублів. Купець, що побажав купити, обурився, що дорого. „Добре, - відповів продавець. Бери коня даром, а заплати тільки за цвяхи на його підковах. А цвяхів у всякій підкові 6 штук. І будеш ти мені платити за них у такий спосіб: за перший цвях 10 копійок, за другий цвях 20 копійок, за третій – 30 копійок і т.д.” Купець же, думаючи, що заплатить набагато менше, чим 25 рублів, погодився.

Чи проторгувався купець, і якщо так, то на скільки?”

                              Відомий німецький математик Карл Гаусс (1777 - 1875) ще у школі виявив блискучі математичні здібності.  Коли йому було 9 років, учитель, прагнучи надовго зайняти дітей, задав на уроці наступну задачу: знайти суму перших ста натуральних чисел. На здивування учителя один з учнів (це був маленький Гаусс ) через хвилину викликнув: “Я вже розв'язав”.

У зошиті Гаусса було тільки одне число, але зате вірне. 

VI Вивчення нового  матеріалу Команда «Теоретики»

 Слово “прогресія” походить від латинського слова “progressio” і означає “рух уперед” (як і слово “прогрес”). Уперше цей термін як математичний вживається у працях римського вченого Боеція (V – VI ст.).

Що означають фрази?

«Частка пенсіонерів у країні росте в арифметичній прогресії…»

« При зростаючій відносній масі ракети … швидкість ракети росте в арифметичній прогресії…»

Учитель. Перша умова, якої треба дотримуватися в математиці, – це бути точним. Друга – бути чітким, і наскільки можливо, простим.

  Отже, ми сьогодні з вами на уроці просто, чітко і з легкістю дамо означення арифметичної прогресії, відповідної термінології (різниця арифметичної прогресії); рекурентної формули та основних властивостей арифметичної прогресії (включаючи характеристичну властивість).Виробимо вміння: відтворювати зміст вивчених понять. А також  закріпимо навички обчислення елементів прогресії, покажемо практичне застосування теми на прикладах історичних задач, задач практичного змісту, будемо удосконалювати вміння оцінювати свої досягнення.

Команда «Практики»

Арифметична прогресія (an) — числова послідовність, у якій кожний наступний член, починаючи з другого, дорівнює попередньому члену, до якого додається те саме число. Це число називають різницею арифметичної прогресії.

Приклад. (а_n): 1; 3; 5; 7; 9 — арифметична прогресія. 

3 – 1 = 5 – 3 = 7 – 5 = 9 – 7 = 2; 2 — різниця арифметичної прогресії. Рекурентна формула арифметичної прогресії: an+1 = аn + d,

d = an+1 – аn - різниця арифметичної прогресії. Якщо d > 0, то прогресія є зростаючою (20; 24; 28; …)

Якщо d < 0, то прогресія є спадною (11; 8; 5; …)

Якщо d = 0, то прогресія є сталою (2; 2; 2; …)

Нехай маємо арифметичну прогресію: -12; -8; -4; 0; 4; … . d = 4. Продовжуючи додавати це число до кожного нового члена, можемо обчислити значення її члена, який стоїть на будь – якому місці. Однак цей шлях громіздкий і не досить раціональний.

Команда « Дослідники»

Ми спробуємо відшукати простіший спосіб розв’язання цієї і подібних задач.

З означення арифметичної прогресії випливає: а₂ = а₁ + d, а₃ = а₂ + d = (а₁ + d) + d =  а₁ + 2d, а₄ = а₃ + d = (а₁ + 2d) + d = а₁ + 3d і т.д.

an = a1 + (n - 1)d – формула загального члена арифметичної прогресії де a_n — n-й член арифметичної прогресії;  а₁ — перший член арифметичної прогресії;  d — різниця арифметичної прогресії;  n — номер члена арифметичної прогресії.

Приклад. Дано: (а_n) — арифметична прогресія, (а_n) : 7,8; 8,9; 10; ....

 Знайти: а₉

Розв'язання а₁ = 7,8; a₂ = 8,9;a₃ = 10: d = a₃ – a₂ = 10 – 8,9 = 1,1. a_n = a₁ + d(n – 1). a₉ = 7,8 + 1,1(9 – 1) = 7,8 + 8,8 = 16,6.

Відповідь: а₉ = 16,6.

Властивості арифметичної прогресії

1.Кожний  член арифметичної прогресії, починаючи з другого, є середнім арифметичним двох сусідніх  членів, тобто а_n.

2.                      Якщо (а_n) — арифметична прогресія (скінченна), то сума двох членів, рівновіддалених від  її кінців, є  величиною сталою .

 

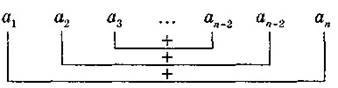
Теорема Гаусса: Сума двох членів скінченної арифметичної прогресії, які рівновіддалені від її кінців дорівнює сумі крайніх членів цієї прогресії, тобто а1+аn=ак+аn+1-k=const.

3.                      Теорема*. Будь-яка арифметична прогресія (а_n) може бути задана формулою a_n = kn + b, де k і b — деякі числа; і навпаки, якщо послідовність (а_n) задана формулою a_n = kn + b, де k і b — деякі числа, то ця послідовність є арифметичною прогресією.Команда «Філософи» Тепер ми запропонуємо розв’язки попередніх задач.

Задача Гаусса. Знайти суму перших ста натуральних чисел.

Як міркував маленький Гаусс? Зміркувавши, що суми 1+100, 2+99 і т. д. рівні, він помножив 101 на 50, тобто число таких сум, яке дорівнює 5050. Інакше кажучи, він помітив закономірність, яка властива арифметичній прогресії.  Формули суми n членів арифметичної прогресії:

 

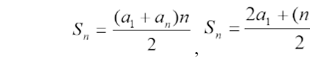
Задача 1. Розв’язання. Нехай І чоловік отримав х міри ячменю, а різниця у=1/8 .

Тоді 

S= (2x+(n-1)d)/2*n=(2x+9*1/8)/2*10; (16x+9)/16*10=10; 16x+9=16; 16x=7; x=7/16. 

I чол. -7/16; II чол.-9/16; III чол. -11/16 ; IV чол. -13/16; V чол. -  15/16; VI чол. –  17/16;  VII чол. -1 9/16; VIII чол. - 21/16; IX чол. - 23/16; X чол. - 25/16  .

Відповідь:7/16 міри; 9/16 міри; 11/16 міри; 13/16 міри; 15/16 міри; 17/16 міри; 19/16 міри; 21/16 міри; 23/16 міри; 25/16 міри.

Задача 2. Розв’язання. Нехай х – частка першого брата, а d – на стільки піднімається брат над братом. Тоді

  S =(2x+(n-1) d)/2*n=(2x+9*d)/2*10;  (2x+9*d)*5=100; 

 2x+9d=20; а₈  =х+7d=6; х=6-7d; 2(6-7d)=20; 12-14d+9d=20; -5d=8; d= -1,6.

Х=6+11,2=17,2 мел. 

I брат – 17,2 мел., II брат – 15,6 мел.; III брат – 14 мел.; IV брат – 12,4 мел. V брат – 10,8 мел.; VI брат – 9,2 мел.; VII брат – 7,6 мел.; VIII брат – 6 мел.; IX брат – 4,4 мел.  і X брат – 2,8 мел.  

Відповідь:17,2мел.;  15,6 мел.; 14 мел.; 12,4 мел.; 10,8 мел., 9,2 мел.; 7,6 мел.; 6 мел.; 4,4 мел.; 2,8 мел. Задача 3. Розв’язання

а1= 10 коп., а d = 10 коп.  Всіх цвяхів у коня 6*4=24 цвяхи. Знайти S24  

                                      S *24= 250*12= 3000 коп.=30 руб. 

Купець проторгувався на 5 рублів.

Учитель. 1) «Мікрофон» 

1.   Дайте означення арифметичної прогресії.

2.   Як називають стале число d для такої послідовності?

 3.Чому дорівнює число d ?

4.                        Як перевірити чи є число членом арифметичної прогресії? ( Якщо різниця між наступним і попереднім членом послідовності одне й теж число, то дана послідовність є арифметичною).

5.                        Назвіть формулу n-го члена арифметичної прогресії.

6.                        У чому полягає характеристична властивість арифметичної прогресії. (Кожний член арифметичної прогресії, починаючи із другого рівний середньому арифметичному двох сусідніх з ним членів).

7.                        Назвіть формули суми п-перших членів арифметичної прогресії.

8.                        За якою формулою можна знайти будь-який член арифметичної прогресії?

9.                        Якою є арифметична прогресія, якщо d < 0, d > 0,    d = 0?

10.                   Як перевірити, чи є послідовність арифметичною прогресією?

11.                   Що можна знайти в арифметичній прогресії, знаючи d   та а₁? Названі формули занесемо в таблицю.

	Арифметична прогресія
Визначення	an1 an d
Формула n-го члена	an a1 d(n1)
Характеристична властивість	a an  n1 an1 2
Формула суми n членів	(a Sn  1 an)n  Sn  2a1  (n 1)d n                          2                            2

 

VII Закріплення вивченого матеріалу Тести

Команда «Теоретики» 1. З вказаних послідовностей арифметичною прогресією є...

     а) 45; 15; 5; 0...;            б) 4; 9; 9; 4...;         

     в) 2; 4; 8; 16...;              г) 15; 17; 19; 21...

2.                   Якщо перший член арифметичної прогресії дорівнює 8, а різниця 3, то другий її член дорівнює...

                    а) 5;       б) 24;       в) 8/3;         г)  11

3.                   Якщо третій член арифметичної прогресії    дорівнює 15 і різниця 4, то четвертий її член дорівнює...

   а)  11;      б) 60;     в) 19;      г) 15/4

4.                   У заданій арифметичній прогресії 3; 7; 11; 15 другим членом є число...    а) 3;         б) 7;         в)  10;         г) 4

5.                   Якщо арифметична прогресія (𝑎_𝑛) зростаюча, то...

     а) 𝑎₁ < а₂;  б) а₁ > а₂;   в) a₁ = a₂;    г) а₁ ≥ а₂;    г) інша відповідь. 

Команда «Практики»

1.     Щоб знайти різницю арифметичної прогресії 4; 7; 10; 13;..., треба...      

         а) 4 + 7;      б) 4 • 7;       в) 4 – 7;     г) 7 – 4

2.     Щоб обчислити а11, якщо а1 =3, d = 8, необхідно...

     а) 3+(8-1)11;        б)   8+(11–1)3;    в) 3+(11-1)8;        г) 8+(3–1)11

3.     Якщо задана арифметична    прогресія і а1 +а21 = 54, то сума а2 +а20  дорівнює...              а) 22;    б) 18;     в) 54;    г) 108.

4.     Якщо а1 =11, а15 =89, то,  щоб  обчислити S15, треба...

    а)   (15+11)/2*89;  б) (15+89)/2*11;  в) (15+11)/89*2;  г) (89+11)/2*15

5.     Знайдіть перший член арифметичної прогресії, якщо п´ятий її член дорівнює 35, а різниця дорівнює 6.

а) 10; б) 11; в) 5; г) 15. 

Команда « Дослідники»

1.                      Дитина будує башту з кубиків так, що у верхньому ряді лежить 1 кубик, у другому – 2 кубики, у третьому – 3 кубики і т.д. Скільки потрібно кубиків, щоб побудувати башту з 12 рядів?

а) 60; б) 72; в) 78; г) 84.

2.                      Визначте номер першого додатного члена арифметичної прогресії:  -32; 

-30;  -28;…

а) 18; б) 17; в) 16; г) 14.

3.                      Знайдіть суму членів арифметичної прогресії із сьомого по дев´ятнадцятий включно, якщо перший член дорівнює 8, а п´ятнадцятий член дорівнює 64.

а) 696; б) 728; в) 836; г) 848.

4.                      Знайдіть номер члена арифметичної прогресії, який дорівнює 29, якщо перший член дорівнює 5, а різниця дорівнює 3.

а) 8; б) 9; в) 7; г) 10.

5.                      Знайдіть суму перших восьми членів арифметичної прогресії, якщо перший її член дорівнює 2,5, а різниця дорівнює  -2.

а) 56; б) 72; в) -36; г)  -72.

Команда «Філософи»

ЗАДАЧА ПРО СТО МІР ХЛІБА.                                               

Сто мір хліба розділити між п´ятьма людьми так, щоб другий одержав на стільки ж більше від першого, на скільки третій одержав більше від другого, четвертий від третього, а п´ятий від четвертого. Крім того, двоє перших мають одержати в 7 разів менше, від трьох інших.

Розв'язання. Нехай х-міра хліба I – ої особи, II –x+d, III-x+2d, IV-x+3d. За умовою: x+x+d+x+2d+x+3d+x+4d=100; 5x+10d=100; x+2d=20; 2d=20-x; Оскільки, двоє перших мають одержати в 7 разів менше, від трьох інших, то маємо друге рівняння:7(x+x+d)=x+2d+x+3d+x+4d; 14x+7d=3x+9d; 11x=2d; 11x=20-x; 12x d. I особа - міри;   II -  III - (мір);  IV – (міри).

             Відповідь:   міри;   10 20 мір;  міри.

Піраміди для фараонів. Будуючи піраміди для фараонів, єгиптяни в кожному наступному ряду плит встановлювали на одну плиту менше, ніж в попередньому. На самому верху стіни підноситься одна плита. Скільки всього плит знадобиться тільки для однієї стіни піраміди, якщо плити стоять в 60 рядів? Розв'язання a_n = а₁+59* (-1) = 1; а₁= 1+59=60 пл. 

                     S 3660 пл.

Відповідь: 3660 плит.

СТАРОДАВНЯ ЗАДАЧА.                                                                 

Людям, які копають криницю, обіцяно за  перший                                                  метр заплатити 30 крб., а за кожний наступний – на  20 крб більше, ніж за попередній метр. Скільки вони  одержать за копання 12-метрової криниці?

Розв’язання.

  S₁₂ = (2а₁ + (12-1)*d):2*12=( 60+11*20):2*12= 140*12=1680 грн. 

Відповідь: 1680 грн.

ЗАДАЧА ФЕОФАНА ПРОКОПОВИЧА. 

Якась людина має багато коней, і всім їм різна ціна. Найгірший кінь коштує 4 золотих, а найкращий – 55 золотих, і ціна від одного до другого коня весь час зростає на 3 золотих. 

Питаємо: скільки ж усього було коней?

Розв’язання. 

Нехай а₁₌ 4 злотих,  а_n =55 злотих, d=3 злотих. a_n=а₁+(n-1)*d;  55=4+3n-3; 54=3n; n=18. 

Відповідь 18 коней.

VIII Домашнє завдання

Вивчити п. 16. Розв’язати: № 673(а, г), № 675 (в, г), №676 (а, в), № 677 (а, в). IX Підсумок уроку (Учні підсумовують свою роботу та оцінюють).

1.                     Що нового ви дізналися на уроці? 

2.                     Чи досягли очікуваних результатів?

Література

1.                     Бевз Г.П., Бевз В.Г. Алгебра, 9. -К.:Зодіак-ЕКО,2018.

2.                     Мерзляк А. Г., Полонський В.Б., Якір М., С. Алгебра, 9. –Х.:

«Гімназія»,2018. 

3.                     Журнал «Математика в школах України».- 2006. -№33. –с. 17-19.