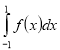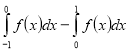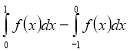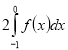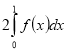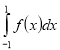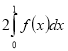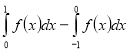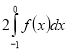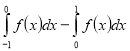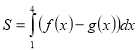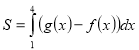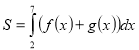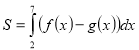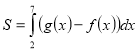III. Функції. Частина 8. Первісна та визначений інтеграл. Застосування визначеного інтеграла до обчислення площ плоских фігур
Первісна та визначений інтеграл. Застосування визначеного інтеграла до обчислення площ плоских фігур.
(2006)30. Річка тече лугом і двічі перетинає шосе, утворюючи криву ![]() . Яка площа лугу між шосе та річкою (у км2), якщо вважати, що лінія шосе збігається з віссю
. Яка площа лугу між шосе та річкою (у км2), якщо вважати, що лінія шосе збігається з віссю ![]() (див. рисунок)? Одиниця довжини –
(див. рисунок)? Одиниця довжини – ![]() км.
км.
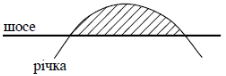
Відповідь: ![]() .
.
(2007)15. Знайдіть первісну функції ![]() , графік якої проходить через точку з координатами
, графік якої проходить через точку з координатами ![]() .
.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
Відповідь: Б.
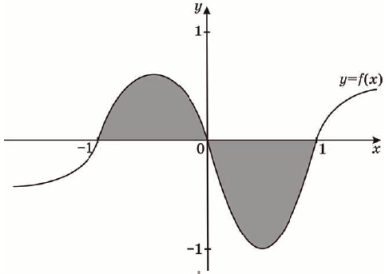
(2008)19. На рисунку зображено графік функції ![]() . Укажіть формулу для обчислення площі зафарбованої фігури.
. Укажіть формулу для обчислення площі зафарбованої фігури.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
Відповідь: Б.
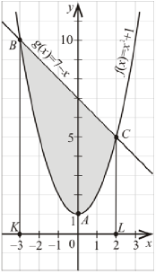
(2009)32. Задано функції ![]() і
і ![]() .
.
1. Знайдіть абсциси точок перетину графіків функцій ![]() і
і ![]() . У прямокутній системі координат зобразіть фігуру, обмежену цими графіками.
. У прямокутній системі координат зобразіть фігуру, обмежену цими графіками.
2. Обчисліть площу фігури, обмеженої графіками функцій ![]() і
і ![]() .
.
Відповідь: 1. ![]() ;
; ![]() ; 2.
; 2. ![]() (кв. од.).
(кв. од.).
(2010)32. Обчисліть інтеграл 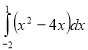 .
.
Відповідь: ![]() .
.
(2010)32. Обчисліть інтеграл 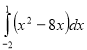 .
.
Відповідь: ![]() .
.
(2010)32. Обчисліть інтеграл 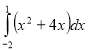 .
.
Відповідь: ![]() .
.
(2010)34. Обчисліть площу фігури, обмеженої лініями ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Відповідь: ![]() .
.
(2010)34. Обчисліть площу фігури, обмеженої лініями ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Відповідь: ![]() .
.
(2010)34. Обчисліть площу фігури, обмеженої лініями ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Відповідь: ![]() .
.
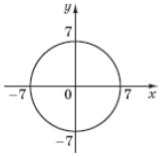
(2012)30. Обчисліть 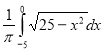 , використовуючи рівняння кола
, використовуючи рівняння кола ![]() , зображеного на рисунку.
, зображеного на рисунку.
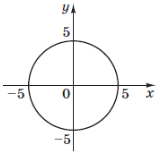
Відповідь: ![]() .
.
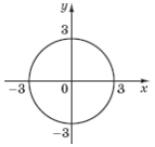
(2012)30. Обчисліть 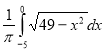 , використовуючи рівняння кола
, використовуючи рівняння кола ![]() , зображеного на рисунку.
, зображеного на рисунку.
Відповідь: ![]() .
.
(2012)30. Обчисліть 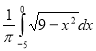 , використовуючи рівняння кола
, використовуючи рівняння кола ![]() , зображеного на рисунку.
, зображеного на рисунку.
Відповідь: ![]() .
.
(2012)30. Обчисліть  , використовуючи зображений на рисунку графік лінійної функції
, використовуючи зображений на рисунку графік лінійної функції ![]() .
.

Відповідь: ![]() .
.
(2012)30. Обчисліть 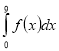 , використовуючи зображений на рисунку графік лінійної функції
, використовуючи зображений на рисунку графік лінійної функції ![]() .
.
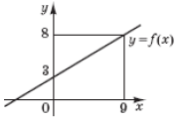
Відповідь: ![]() .
.
(2012)30. Обчисліть 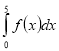 , використовуючи зображений на рисунку графік лінійної функції
, використовуючи зображений на рисунку графік лінійної функції ![]() .
.
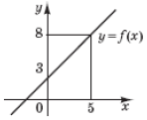
Відповідь: ![]() .
.
(2013)30. Обчисліть площу фігури, обмеженої графіком функції ![]() і прямими
і прямими ![]() ,
, ![]() та
та ![]() .
.
Відповідь: ![]() .
.
(2013)30. Обчисліть площу фігури, обмеженої графіком функції ![]() і прямими
і прямими ![]() ,
, ![]() та
та ![]() .
.
Відповідь: ![]() .
.
(2013)30. Обчисліть площу фігури, обмеженої графіком функції ![]() і прямими
і прямими ![]() ,
, ![]() та
та ![]() .
.
Відповідь: ![]() .
.
(2014)32. На рисунку зображено ескіз графіка квадратичної функції ![]() . Площа криволінійної трапеції, обмеженої лініями
. Площа криволінійної трапеції, обмеженої лініями ![]() ,
, ![]() ,
, ![]() ,
, ![]() , дорівнює
, дорівнює ![]() кв. од. Обчисліть суму
кв. од. Обчисліть суму ![]() .
.
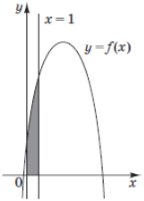
Відповідь: ![]() .
.
(2014)32. На рисунку зображено ескіз графіка квадратичної функції ![]() . Площа криволінійної трапеції, обмеженої лініями
. Площа криволінійної трапеції, обмеженої лініями ![]() ,
, ![]() ,
, ![]() ,
, ![]() , дорівнює
, дорівнює ![]() кв. од. Обчисліть суму
кв. од. Обчисліть суму ![]() .
.

Відповідь: ![]() .
.
(2014)32. На рисунку зображено ескіз графіка квадратичної функції ![]() . Площа криволінійної трапеції, обмеженої лініями
. Площа криволінійної трапеції, обмеженої лініями ![]() ,
, ![]() ,
, ![]() ,
, ![]() , дорівнює
, дорівнює ![]() кв. од. Обчисліть суму
кв. од. Обчисліть суму ![]() .
.

Відповідь: ![]() .
.
(2014)19. На рисунку зображено графік неперервної функції ![]() . Укажіть формулу для обчислення площі зафарбованої фігури.
. Укажіть формулу для обчислення площі зафарбованої фігури.
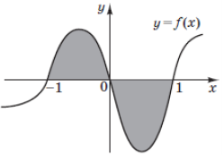
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
Відповідь: Д.
(2014)32. Усі вершини трапеції ![]() належать графіку функції
належать графіку функції ![]() , побудованому в прямокутній декартовій системі координат. Більша основа
, побудованому в прямокутній декартовій системі координат. Більша основа ![]() лежить на осі
лежить на осі ![]() . Яку найбільшу площу може мати трапеція
. Яку найбільшу площу може мати трапеція ![]() ?
?
Відповідь: ![]() .
.
(2014)32. Усі вершини трапеції ![]() належать графіку функції
належать графіку функції ![]() , побудованому в прямокутній декартовій системі координат. Більша основа
, побудованому в прямокутній декартовій системі координат. Більша основа ![]() лежить на осі
лежить на осі ![]() . Яку найбільшу площу може мати трапеція
. Яку найбільшу площу може мати трапеція ![]() ?
?
Відповідь: ![]() .
.
(2014)32. Усі вершини трапеції ![]() належать графіку функції
належать графіку функції ![]() , побудованому в прямокутній декартовій системі координат. Більша основа
, побудованому в прямокутній декартовій системі координат. Більша основа ![]() лежить на осі
лежить на осі ![]() . Яку найбільшу площу може мати трапеція
. Яку найбільшу площу може мати трапеція ![]() ?
?
Відповідь: ![]() .
.
(2015)34. Визначте додатне значення параметра ![]() , за якого площа фігури, обмеженої лініями
, за якого площа фігури, обмеженої лініями ![]() (див. рисунок),
(див. рисунок), ![]() та
та ![]() , дорівнює
, дорівнює ![]() кв. од.
кв. од.
Відповідь: ![]() .
.
(2015)34. Визначте додатне значення параметра ![]() , за якого площа фігури, обмеженої лініями
, за якого площа фігури, обмеженої лініями ![]() (див. рисунок),
(див. рисунок), ![]() та
та ![]() , дорівнює
, дорівнює ![]() кв. од.
кв. од.

Відповідь: ![]() .
.
(2015)34. Визначте додатне значення параметра ![]() , за якого площа фігури, обмеженої лініями
, за якого площа фігури, обмеженої лініями ![]() (див. рисунок),
(див. рисунок), ![]() та
та ![]() , дорівнює
, дорівнює ![]() кв. од.
кв. од.

Відповідь: ![]() .
.
(2016)16. Використовуючи формулу Ньютона-Лейбніца, обчисліть 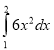 .
.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
Відповідь: Б.
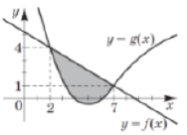
(2016)20. На рисунку зображено графіки функцій ![]() і
і ![]() . Укажіть формулу для обчислення площі зафарбованої фігури.
. Укажіть формулу для обчислення площі зафарбованої фігури.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
Відповідь: Г.
(2017)31. Задано функцію ![]() .
.
1. Визначте координати точок перетину графіка функції ![]() з осями координат.
з осями координат.
2. Побудуйте графік функції ![]() .
.
3. Запишіть загальний вигляд первісних для функції ![]() .
.
4. Обчисліть площу фігури, обмеженої графіком функції ![]() та осями
та осями ![]() і
і ![]() .
.
Відповідь: 1. ![]() ,
, ![]() ; 3.
; 3. ![]() ; 4.
; 4. ![]() .
.
(2017)18. Обчисліть інтеграл 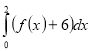 , якщо
, якщо 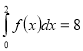 .
.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
Відповідь: А.
(2018)31. Задано функції ![]() і
і ![]() .
.
1. Побудуйте графік функції ![]() .
.
2. Побудуйте графік функції ![]() .
.
3. Визначте абсциси точок перетину графіків функцій ![]() і
і ![]() .
.
4. Обчисліть площу фігури, обмеженої графіками функцій ![]() і
і ![]() .
.
Відповідь: 3. ![]() ,
, ![]() ; 4.
; 4. ![]() .
.
(2018)31. Задано функції ![]() і
і ![]() .
.
1. Побудуйте графік функції ![]() .
.
2. Побудуйте графік функції ![]() .
.
3. Визначте абсцису точки перетину графіків функцій ![]() і
і ![]() .
.
4. Обчисліть площу фігури, обмеженої графіками функцій ![]() і
і ![]() та віссю
та віссю ![]() .
.
Відповідь: 3. ![]() ; 4.
; 4. ![]() .
.


про публікацію авторської розробки
Додати розробку