Індивідуальна робота "Теорія границь"

Індивідуальна робота 1 «Теорія границь»

Завдання 1. Знайти границю .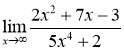

Завдання 2. Знайти границю .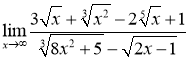

Завдання 3. Знайти .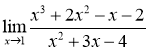

Завдання 4. Обчислити .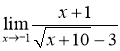

Завдання 5. Обчислити .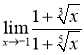

Завдання 6. Обчислити .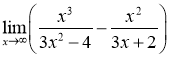

Завдання 7. Обчислити .

Завдання 8. Знайти границю .

Завдання 9. Знайти .

Завдання 10. Обчислити границю .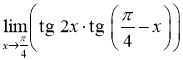

Завдання 11. Обчислити .

Завдання 12. Обчислити .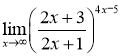

Завдання 13. Обчислити .

Завдання 14. Обчислити .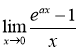

Завдання 15. Обчислити границю .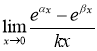

Завдання 16. Обчислити .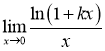

Завдання 17. Обчислити .

Розв’язання та відповіді до завдань

Розв’язання 1. Маємо невизначеність виду , задану відношенням многочленів. Старший степінь цих многочленів – четвертий, тому поділимо чисельник та знаменник дробу під знаком границі на . Отримуємо:

.

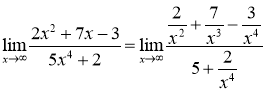Застосуємо до отриманого виразу теорему про границю частки:

.

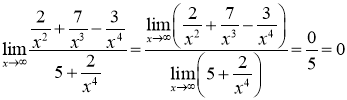Тут ми використали для границь у чисельнику та знаменнику теорему про границю суми функцій, а також врахували те, що , , , є нескінченно малими величинами. Таким чином, .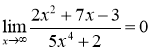

При знаходженні границь, аналогічних границі прикладу 2.29, доцільно використовувати наступне правило. Якщо степінь чисельника дробу є меншою, ніж степінь знаменника, то границя дорівнює нулю; якщо степінь чисельника дорівнює степені знаменника, то границя дорівнює відношенню коефіцієнтів при старших степенях чисельника та знаменника; якщо степінь чисельника більший за степінь знаменника, то границя дробу дорівнює нескінченності.

Розв’язання 2. У цьому прикладі вираз під знаком границі є відношенням ірраціональних функцій, утворюючи при невизначеність виду . Старший степінь чисельника дорівнює (доданок ), старший степінь знаменника також дорівнює (), тому поділимо чисельник та знаменник дробу на . Отримаємо:

.

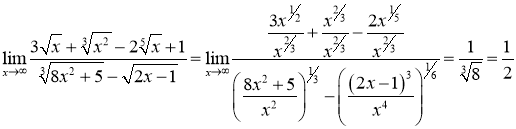Невизначеність виду при задана відношенням двох многочленів. У цьому випадку потрібно розкласти чисельник і знаменник на множники . Оскільки при чисельник та знаменник дробу дорівнюють нулю, то у їхньому розкладу на множники присутній множник . Скорочення на степінь можливе, оскільки , але . Після такого скорочення невизначеність усувається.

Розв’язання 3. Розкладемо на множники чисельник та знаменник дробу під знаком границі. Маємо:

.

Коренями квадратного тричлена є , , тому його розклад на множники має вигляд:

.

Підставивши знайдені розклади на множники у задану границю, отримуємо:

.

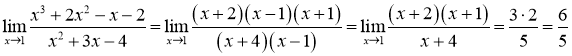Невизначеність виду при задана відношенням ірраціональних виразів. Для розкриття таких невизначеностей звичайно позбавляються від ірраціональності у чисельнику або знаменнику.

Розв’язання 4. Позбудемося ірраціональності у знаменнику. Маємо:

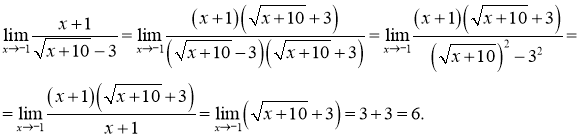
Від ірраціональності можна позбавитися також шляхом введення нової змінної.

Розв’язання 5. Маємо невизначеність виду . Щоб позбутися ірраціональності, виконаємо заміну змінної . При , , . Отримаємо:

.

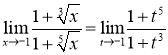Оскільки є коренем чисельника та знаменника дробу, то їх можна поділити націло на . Маємо:

, .

Підставивши ці вирази у останню границю, отримуємо:

.

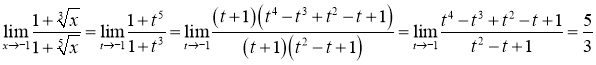 Невизначеність виду задана різницею раціональних дробів або ірраціональних виразів.

Розв’язання 6. Маємо невизначеність виду , утворену різницею раціональних дробів. Виконаємо віднімання:

Отже, .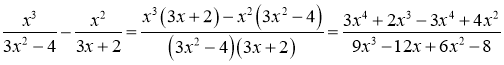

Підставивши знайдену різницю дробів у границю,отримаємо:

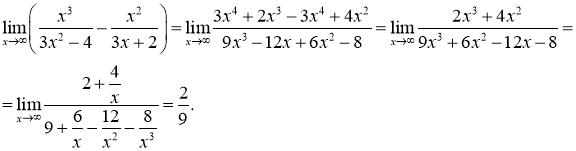
Розв’язання 7. Маємо невизначеність , утворену різницею виразів, що містять ірраціональність. Розкриємо дану невизначеність наступним чином:

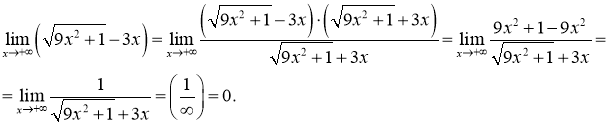
Невизначеності виду , задані виразами, що містять тригонометричні функції, часто розкриваються за допомогою першої важливої границі.

Розв’язання 8. Використовуючи співвідношення , запишемо границю у вигляді: .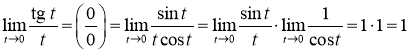

Розв’язання 9. Виконаємо перетворення виразу у чисельнику дробу:

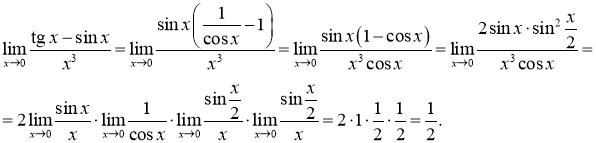
При обчисленні цієї границі було використано формулу (2.17) : при .

Розв’язання 10. У даному прикладі при підстановці замість значення отримуємо невизначеність . Перетворимо її до вигляду . Для цього задану границю запишемо у вигляді:

.

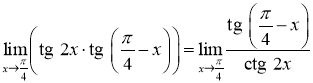Виконаємо заміну змінної . Тоді при ,  тригонометричні вирази у границі набувають вигляду:

,

.

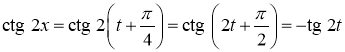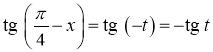Підставимо ці вирази у границю:

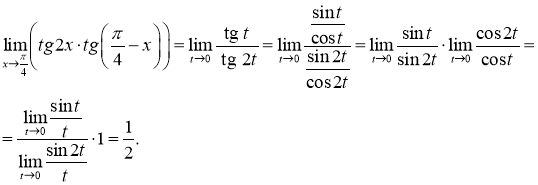
Розв’язання 11. Виконаємо заміну змінної , . При  . Задана границя набуває вигляду:

.

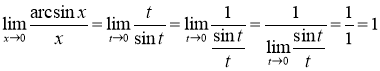При розкритті невизначеності виду використовують другу чудову границю . 

Розв’язання 12. Оскільки , , то обчислення даної границі зводиться до знаходження невизначеності . Застосуємо другу важливу границю 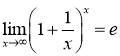. Для цього представимо дріб у вигляді суми одиниці та нескінченно малої величини:

.

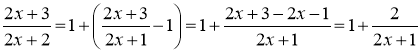Отримуємо:

.

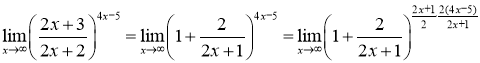Тут у показнику степеня ми виділили величину, , обернену нескінченно малій, що додається до одиниці у основі степеня. Застосовуючи формулу (2.20), знаходимо:

.

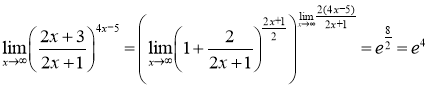Розв’язання 13. Підставивши у вираз під знаком границі , отримуємо невизначеність , тому для розв’язання прикладу використаємо другу важливу границю. Для цього представимо вираз у основі степеня у вигляді суми одиниці та нескінченно малої і виділимо у показнику степеня величину, обернену цій нескінченно малій:

.

Використовуючи формулу (2.20), отримуємо:

.

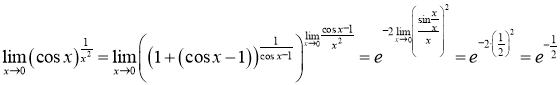8. При розкритті невизначеності у випадках, коли під знаком границі знаходяться логарифмічні або показникові функції, доцільно використовувати формули (2.21) – (2.24).

Розв’язання 14. Підстановка у вираз під знаком границі значення приводить до невизначеності .  Оскільки під знаком границі знаходиться показникова функція, то для обчислення границі можна використати формулу (2.22). Зробимо заміну , . При . Отримуємо:

.

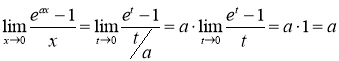Розв’язання 15. Маємо невизначеність і під знаком границі знаходяться показникові функції. Застосувавши формулу (2.22), отримуємо:

.

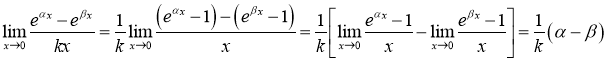Тут ми використали результат, отриманий у попередньому прикладі 2.42 – .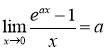

Розв’язання 16. Підстановка у вираз під знаком границі значення визначає невизначеність . Оскільки у виразі під знаком границі знаходиться логарифмічна функція, для розв’язання прикладу доцільно використати формулу (2.21). Виконавши заміну , , отримаємо:

.

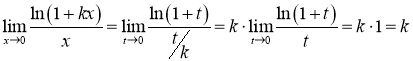Розв’язання 17. Після підстановки у вираз під знаком границі значення маємо невизначеність виду . Зробивши заміну , , отримуємо (при ): 

.

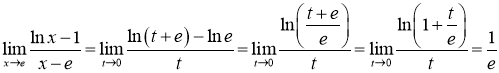Тут ми використали результат прикладу 2.44: 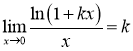, де  .