Презентація "Приріст функції. Задачі, що призводять до поняття похідної"

ПРИРІСТ ФУНКЦІЇ. ЗАДАЧІ, ЩО ПРИВОДЯТЬ ДО ПОНЯТТЯ ПОХІДНОЇ. Вчитель – Ковальова Марина Леонідівна

Епіграф: Розум людський має три ключі, які все відкривають:знання, думка, уява. Віктор Гюго

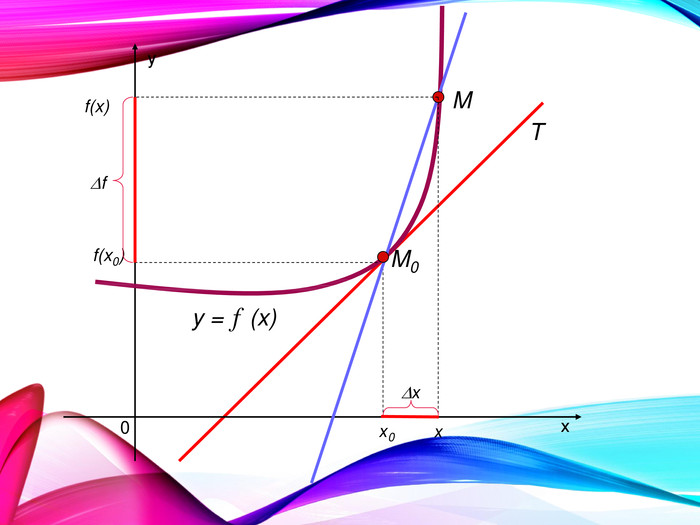
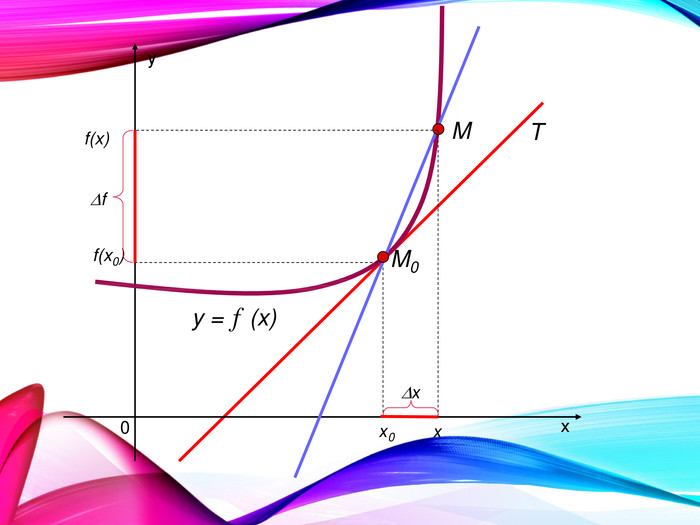
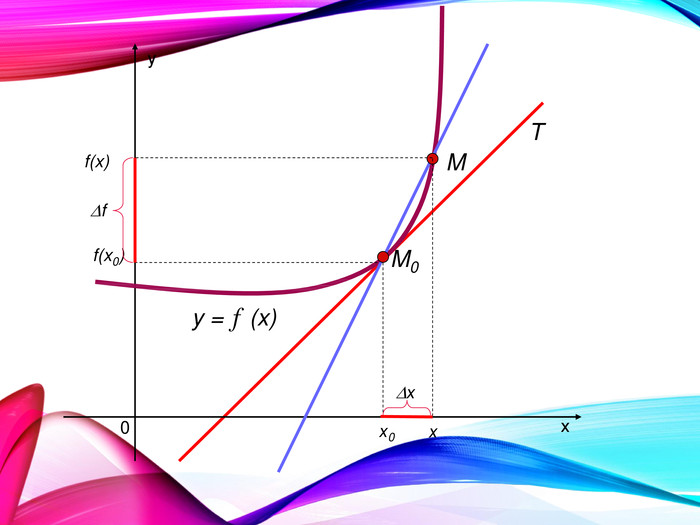
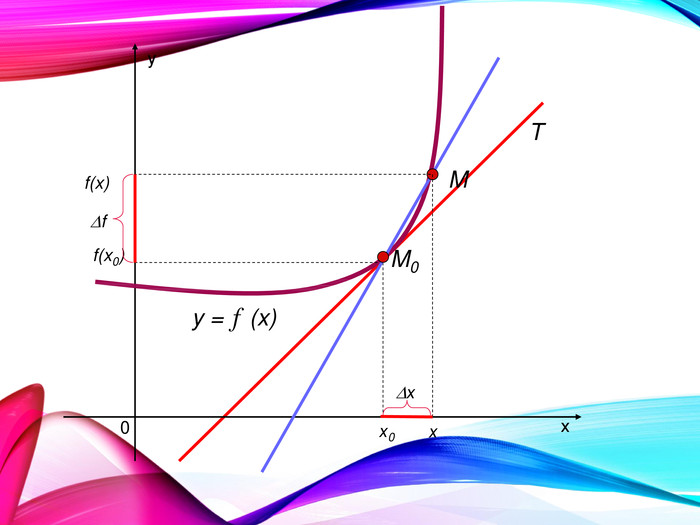
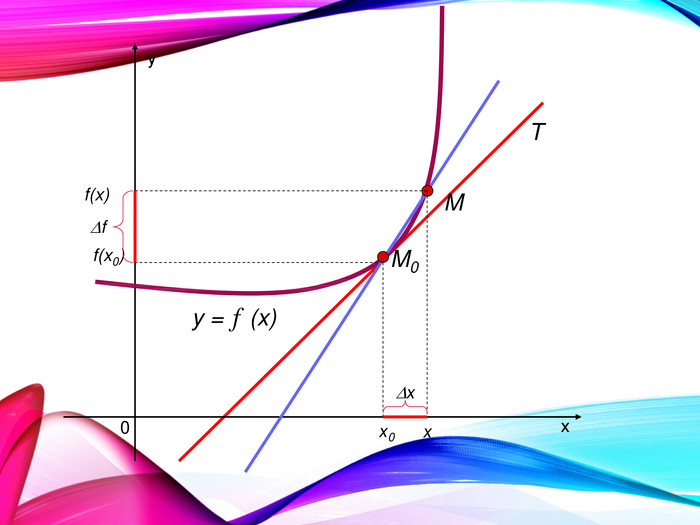
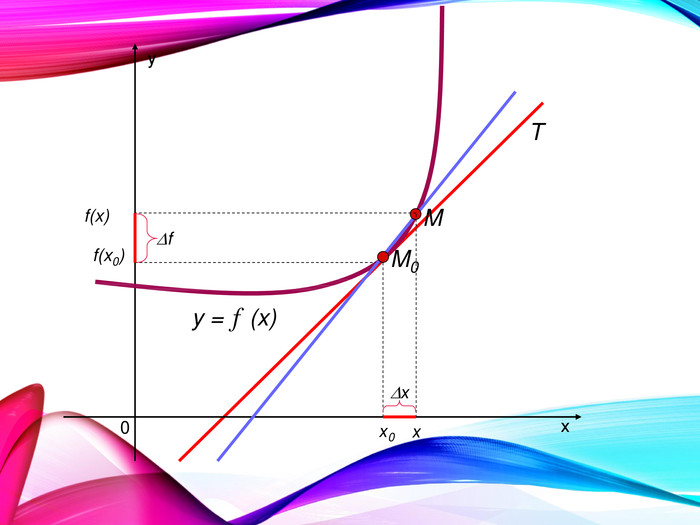
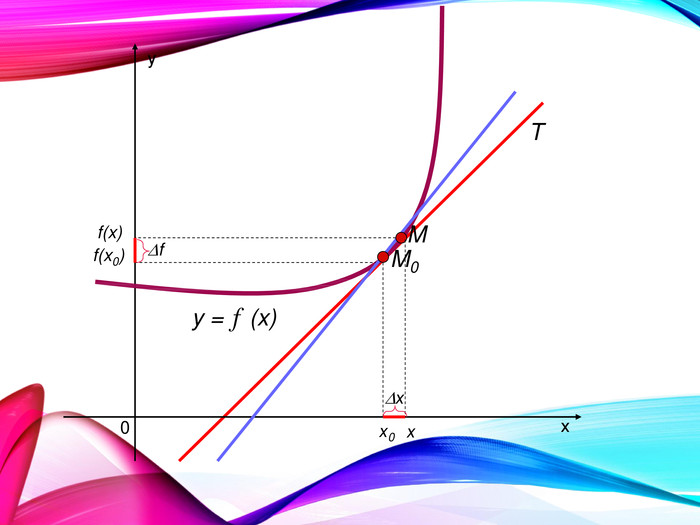
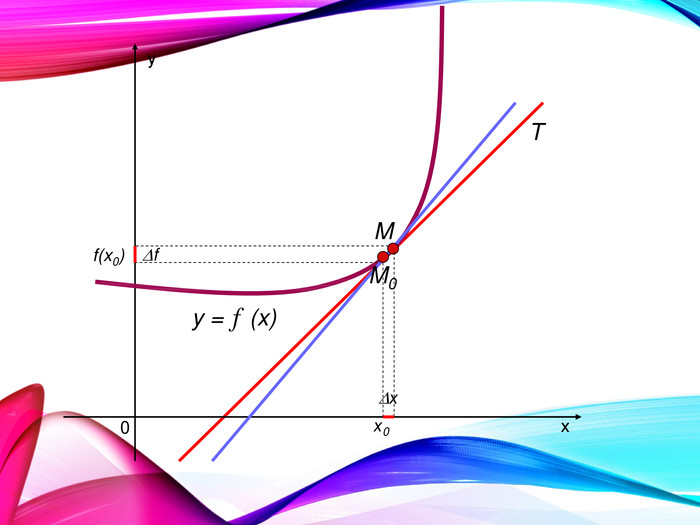
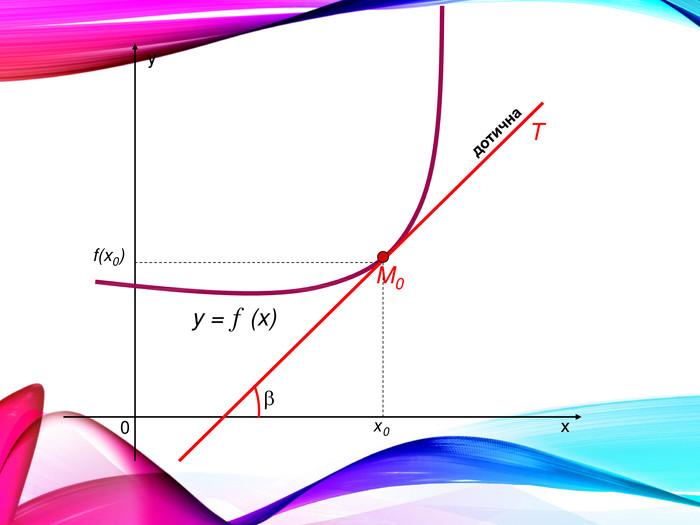
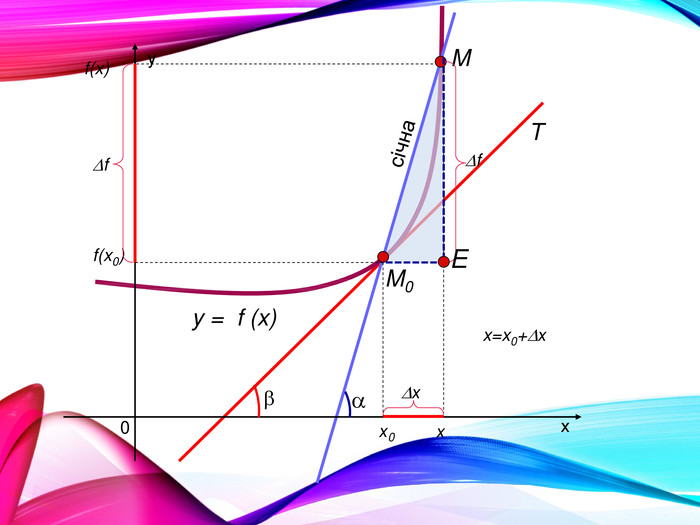
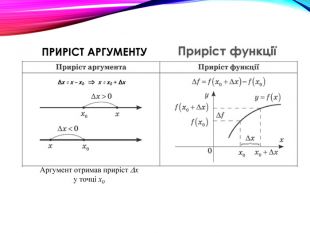
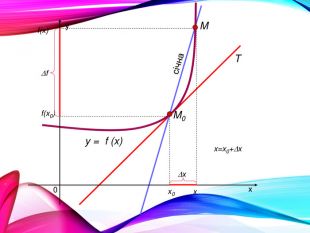
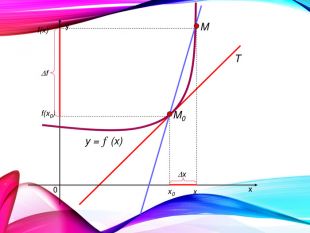
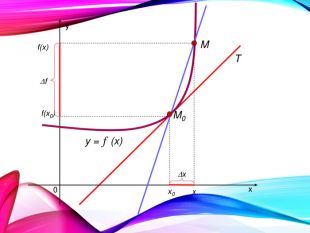
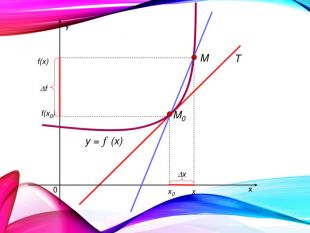
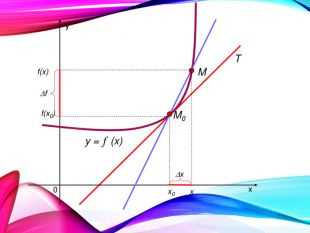
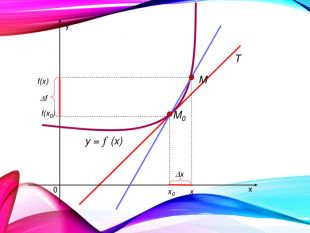
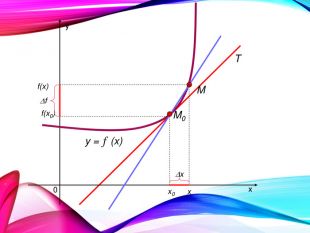
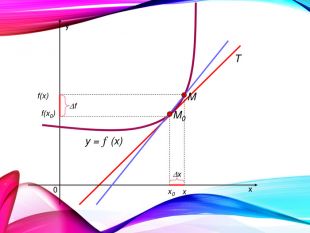
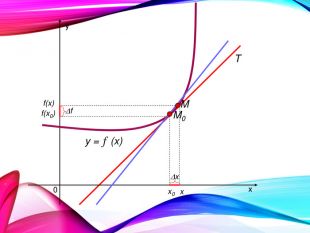
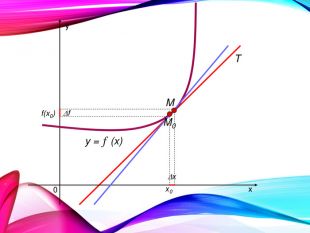
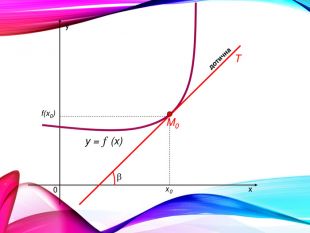
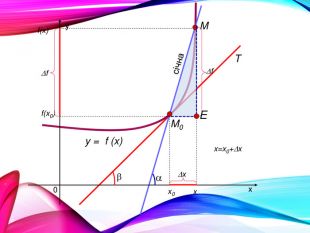
Поняття похідної — фундаментальне поняття математичного аналізу, за допомогою якого досліджують процеси і явища в при­родничих, соціальних і економічних науках. Вивчення різних процесів приводять до необхідності обчислення швидкості зміни різних величин, тобто до поняття похідної. Отже, наша найближча мета — по­знайомитися з поняттям похідної, навчитися знаходити похідні елементарних функцій та застосовувати поняття похідної до до­слідження функцій, вивчення деяких фізичних явищ, до ви­вчення геометричних понять.

НА УРОЦІ: з’ясуємо, що таке приріст функції та приріст аргументу; навчимося знаходити приріст функції; розглянемо задачу про дотичну до графіка функції; розглянемо задачу про миттєву швидкість

ПРИРІСТ АРГУМЕНТУ Приріст функції Аргумент отримав приріст x у точці х0

ПРИКЛАД:

х у о Задача про дотичну до графіка функції

T січна х у 0 y = f (x) х0 f(x0) х х f M0 M x=x0+х f(x)

T х у 0 y = (x) х0 f(x0) х х f M0 M f(x)

T х у 0 y = (x) х0 f(x0) х х f M0 M f(x)

T х у 0 y = (x) х0 f(x0) х х f M0 M f(x)

T х у 0 y = (x) х0 f(x0) х х f M0 M f(x)

T х у 0 y = (x) х0 f(x0) х х f M0 M f(x)

T х у 0 y = (x) х0 f(x0) M0 х х f M f(x)

T х у 0 y = (x) х0 f(x0) M0 х х f M f(x)

T х у 0 y = (x) х0 f(x0) M0 х х f M f(x)

T х у 0 y = (x) х0 f(x0) M0 х f M

х у 0 y = (x) х0 f(x0) M0  T M0 дотична

T січна х у 0 y = f (x) х0 f(x0) х х f M0 M x=x0+х f(x)  f Е 

Кутовий коефіцієнт січної: Кутовий коефіцієнт дотичної:

Задача про миттєву швидкість: