інформаційний паспорт навчальної теми

ЗАБЕЗПЕЧЕННЯ БЕЗПЕРЕРВНОГО НАВЧАННЯ МАТЕМАТИКИ

ШЛЯХОМ ВПРОВАДЖЕННЯ  ЕЛЕМЕНТІВ ДИСТАНЦІЙНОГО НАВЧАННЯ

Інформаційний паспорт  навчальної теми з геометрії для 

10 класу

«Перпендикулярність прямих і площин у просторі»

 

  

 

     За Програмою для загальноосвітніх навчальних закладів, яка затверджена наказом Міністерства освіти і науки України  № 408 від 20.04.2018 року «Про затвердження типової освітньої програми закладів загальної середньої освіти ІІІ сту-

пеня, 10 класи». 
 

Джерело:https://www.pedrada.com.ua/news/4612-zatverdjeno-tipov-osvtn-programi-novo-ukransko-shkoli

 

Тема №2, геометрія 10 клас.

 

Частина 1.

У частині 1 (таблиця 1.1) наведено джерела інформації, за якими учень може самостійно вивчати тему. Для їх вивчення використано перелік підручників, навчальних посібників, які рекомендовані Міністерством освіти і науки України на 2018/2019 навчальний рік. Крім цього до частини включено джерела, рекомендовані для розширення та поглиблення знань з відповідної теми.

 

 

Перелік джерел навчальної інформації     

Таблиця 1.1

№ з/п		Вид		Назва	Автори		Видав-ництво	Рік ви-дан-ня
Основні підручники та навчальні посібники, рекомендовані         Міністерством освіти і науки України
1		Підручник		Математика, 10 клас (алгебра і початки аналізу та геометрія, рівень стандарту)		Бурда М.І., Колесник Т.В, Тарасенкова Н.А	К., Оріон	2018
2		Підручник		Математика (алгебра і початки аналізу та геометрія), 10 клас		Мерзляк А.Г., Номіровський Д.А., Полонський В.Б.	Х., Гімназія	2018
	2. Додаткові підручники та навчальні посібники, рекомендовані         Міністерством освіти і науки України
	3		Підручник	Математика, 10 клас (алгебра і початки аналізу та геометрія, рівень стандарту)	Нелін Є.П.		Х., Ранок	2018
	4		Підручник	Математика, 10 клас (алгебра і початки аналізу та геометрія, рівень стандарту)		Істер О.С.	К,. Генеза	2018
	5		Підручник	Геометрія, 10 клас (Профільний рівень)		Істер О.С., Єргіна О.В.	К., Генеза	2018
	6		Підручник	Геометрія, 10 клас (Профільний рівень)		Мерзляк А.Г., Номіров-ський Д.А., Полонський В.Б.	Х., Гімназія	2018
	7		Збірник	Математика. 10 клас. Збірник самостійних та контрольних робіт.		Корнес А.І., Бабенко  С.П.	Ранок	2018

 

 

3. Додаткові джерела інформації в пошуковій системі  Google - YouTube
https://bila.km.ua/uchnyam-v.../10-klas/.../menu-id-763.html	https://www.youtube.com/watch?v=C_D40UwH1Gw	sva.in.ua/geometria10006.php	https://www.youtube.com/watch?v=VQXuTjxK8jw

 

Поради, щодо опрацювання деяких джерел з таблиці 1.1:

• Для початкового ознайомлення з теоретичним матеріалом скористайся підручниками, зазначеними в пунктах 1 та 2.
• Для узагальнення та перевірки знань із теми перегляньте посібники, зазначені в пунктах 5-6, та збірник, зазначений у пункті 7.

 

Частина 2

Рекомендації для вивчення теми

1. 1  Загальна характеристика теми

Під час вивчення теми відбувається узагальнення та систематизація знань учнів з планіметрії – розділу, що вивчає взаємне розташування прямих і площин в просторі (розглядається перпендикулярність прямих та площини, двох площин тощо).

Окрім того, учні вивчають теореми про взаємозв’язок паралельності та перпендикулярності прямих та площин у просторі, а також опановують знання про перпендикуляр та похилі тощо.

Тема є практичною (під час вивчення істотно підвищується роль задач на обчислення) та пропедевтичною (для опанування понять кутів у просторі та багатогранників), а також відіграє помітну роль у формуванні просторових уявлень учнів і розвитку конструктивності їхнього мислення.

    У таблиці 2.1 подано витяг з навчальної програми щодо змісту 

 навчального матеріалу з теми  та вимог до навчальних досягнень учнів із  

 їх засвоєння.   

   Таблиця 2.1

 

Зміст навчального матеріалу

Навчальні досягнення учнів

Тема №4 «Перпендикулярність прямих і площин у просторі»  Перпендикулярність прямих у просторі. Перпендикулярність прямої і площини. Ознака перпендикулярності прямої і площини. Перпендикуляр і похила. Теорема про три перпендикуляри. Перпендикулярність площин. Ознака перпендикулярності площин. Залежність між паралельністю та перпендикулярністю прямих і площин. Кути у просторі: між прямими , між прямою і площиною, між площинами. Відстані у просторі: від точки до прямої, від точки до площини, від прямої до паралельної їй площини (від точки до фігури), між паралельними площинами,  між мимобіжними площинами, (між двома фігурами). Ортогональне проектування. (Площа ортогональної проекції многокутника). Практичне застосування властивостей паралельності та перпендикулярності прямих і площин.

Учень (учениця): формулює означення перпендикулярних прямих у просторі, прямої, перпендикулярної до площини, перпендикулярних площин; властивості та ознаки перпендикулярних прямих і площин; обгрунтовує  взаємозв язок паралельності й перпендикулярності прямих і площин у просторі; встановлює взаємне розміщення прямих і площин у просторі; застосовує  вивчені властивості та ознаки до     розв язування задач; обчислює відстані й кути в просторі; застосовує  відношення між прямими і площинами у просторі, вимірювання відстаней і кутів у просторі для опису об єктів оточуючого світу.

 

2.       Поради щодо вивчення теми

Зверніть особливу увагу на ознаки перпендикулярності прямої та площини, теорему про три перпендикуляри та ознаку перпендикулярності площин. Доведення ознаки перпендикулярності прямої та площини спирається на логічні й геометричні зв язки та відношення між планіметричними фігурами, розташованими у тривимірному просторі.

Не забувайте , що під час вивчення теореми про три перпендикуляри необхідно довести і першу, і другу частини теореми, а також розібрати її на малюнках, якщо в основі лежить прямокутний, рівнобедрений та довільний трикутники.

Зверніть увагу на використання теореми Піфагора і насідків з неї в ході розв язування задач на похилу.

2.       Словник до теми

      Визначення основних понять, які зустрічаються в процесі вивчення теми, подано за виданням:

Пряма називається перпендикулярною до площини, якщо вона перетинає цю площину і перпендикулярна до будь-якої прямої, яка лежить у площині і проходить через точку перетину.

Теорема (ознака перпендикулярності прямої і площини).

Якщо пряма, яка перетинає площину, перпендикулярна до двох прямих цієї площини, що проходять через точку перетину, то вона перпендикулярна до площини.

Перпендикуляром, проведеним з даної точки до даної площини, називається відрізок, що сполучає дану точку з точкою площини і лежить на прямій, перпендикулярній до площини.

Теорема (властивості перпендикуляра і похилої).

Якщо з точки, взятої поза площиною, проведені до площини перпендикуляр і похилі, то:

•  перпендикуляр коротший за будь-яку похилу;
•  проекції рівних похилих рівні і, навпаки, похилі, що мають рівні проекції, рівні;
•  з двох похилих більша та, проекція якої більша.

Теорема (про три перпендикуляри).

Якщо пряма, проведена на площині через основу похилої, перпендикулярна до її проекції, то вона перпендикулярна і до самої похилої.

Теорема (обернена до теореми про три перпендикуляри).

Якщо пряма, проведена на площині через основу похилої, перпендикулярна до похилої, то вона перпендикулярна і до проекції похилої.

Теорема (про паралельні прямі та перпендикулярну площину).

Якщо площина перпендикулярна до однієї з двох паралельних прямих, то вона перпендикулярна і до другої.

Теорема (про паралельні площини та перпендикулярну пряму).

Якщо пряма перпендикулярна до однієї з паралельних площин, то вона перпендикулярна і до другої.

Кутом між площинами , які перетинаються, називається кут між прямими, проведеними в цих площинах зі спільної точки перпендикулярно до лінії їх перетину.

3.       Інформація для запам`ятовування.

     Дві прямі називаються перпендикулярними, якщо вони перетинаються під прямим кутом.

      Якщо дві прямі, які перетинаються, паралельні відповідно двом іншим перпендикулярним прямим, то інші прямі теж перпендикулярні.

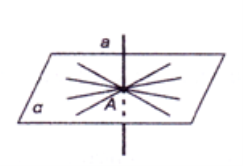Через будь-яку точку прямої в просторі можна провести безліч перпендикулярних до неї прямих. (Усі прямі лежать у площині, яка перпендикулярна до даної прямої та перетинає її у даній точці.)

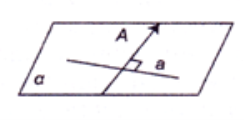Через будь-яку точку в просторі, що не належить даній прямій, можна  провести пряму, перпендикулярну до даної, і тільки одну. Це буде та перпендикулярна до даної прямої пряма, яка лежить  у площині, визначеній даними прямою й точкою.

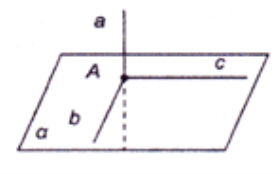Зверніть увагу, що в просторі дві прямі, перпендикулярні до однієї і тієї самої прямої, необов язково паралельні між собою.

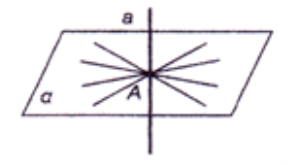Пряма, яка перетинає площину, називається перпендикулярною  до цієї площини, якщо вона перпендикулярна до будь-якої прямої, що лежить у цій площині й проходить через точку перетину.

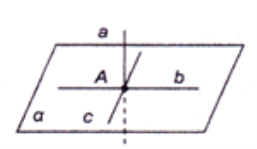Пряма, яка перетинає площину, називається перпендику-лярною до цієї площини, якщо вона перпендикулярна до будь-якої прямої, що лежить у цій площині й проходить через точку перетину. 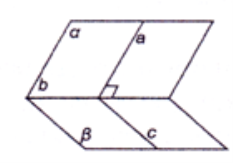На рисунку a перпендикулярна  до площини,  але  a не перпендикулярна до d , зокрема не перпендикулярна до c .

         Через дану точку площини можна провести одну, й тільки одну, перпендикулярну до неї пряму.

         Через дану точку прямої можна провести одну, й тільки одну, перпендикулярну до неї площину.

         Через точку, яка не лежить на прямій, можна провести одну, й тільки одну, площину, перпендикулярну до даної прямої.

         Якщо площина перпендикулярна до однієї з двох паралельних прямих, то вона перпендикулярна й до другої.

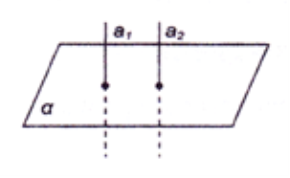Дві прямі, перпендикулярні до однієї й тієї ж площини, паралельні.

Частина 3

Додаткові навчальні матеріали

Для вивчення теми рекомендовано використати додаткові навчальні матеріали. Їх подано, як додатки, перелічено в таблиці 3.1 і розміщено на ком пакт-диску.

 

Номер додатка	Назва додатка
Додаток 3.1	Двогранний кут (презентація у форматі  Mikrosoft Office Power Point)       www.10minclass.com/video/885
Додаток 3.2	Опорний конспект з теми (презентація у форматі  Mikrosoft Office Power Point)
Додаток 3.3	Опорний конспект уроку узагальнення та систематизації знань з теми (презентація у форматі  Mikrosoft Office Power Point), тести онлайн https://videouroki.net/tests/pierpiendikuliarnost-priamykh-i-ploskostiei.html
Додаток 3.4	Відеопрезентація з теми (у форматі Movie Maker) https://videouroki.net/tests/geometria/?uc=679&uct=43748

                         

Частина 4

Самоперевірка знань

Для самоперевірки набутих учнем знань наведено контрольну роботу. (Додаток 4.1)

Частина 5

Творчі роботи

Для поглибленого вивчення  теми пропонується підготувати такі реферати:

1. Перпендикулярність прямих і площин у архітектурі.
2. Застосування прямих і площин у народній творчості (ковані вироби, дерев яне начиння та прикраси).
3. Застосування перпендикулярних прямих та площин у ювелірному виробництві та медицині (оброблення ювелірних виробів, напівдорогоцінних та дорогоцінних каменів).
4. Застосування перпендикулярності прямих та площин у техніці.
5. Застосування перпендикулярності прямих та площин у деревообробній та металургійній промисловості.

 

Частина 6

Джерела методичної інформації

У таблиці 6.1 наведено джерела інформації методичного характеру, визначені та рекомендовані для використання вчителем у висвітленні теми.

(Таблиця 6.1)

№з/п	Вид	Назва		Автори		Видав-ництво		Рік видан-ня
1. Джерела інформації, рекомендовані автором
1	Посібник		Майстер-клас. Геометрія. 10 клас (академічний рівень)		Корнієн-ко Т.А., Фіготіна В.І.		Ранок	2010
2	Посібник		Тести зі стереометрії онлайн		Брод-ський Я.С.		ТМ «Розум-ники»	2017
3	Комплект		Математика. Довідник +Тести, підготовка доДПА, ЗНО		Істер О.С.		К,. Генеза	2018

Частина 7

Додаткові методичні матеріали У таблиці 7.1 запропоновано додаткові методичні матеріали, які можуть бути використані у навчальній роботі. Їх розміщено у формі додатків до частини 7.

Номер додатку	Назва додатку
Додаток 7.1	Методичні картки уроків

 

(Додаток 2.1).

Пряма називається перпендикулярною до площини, якщо вона перетинає цю площину і перпендикулярна до будь-якої прямої, яка лежить у площині і проходить через точку перетину.

Теорема (ознака перпендикулярності прямої і площини).

Якщо пряма, яка перетинає площину, перпендикулярна до двох прямих цієї площини, що проходять через точку перетину, то вона перпендикулярна до площини.

Перпендикуляром, проведеним з даної точки до даної площини, називається відрізок, що сполучає дану точку з точкою площини і лежить на прямій, перпендикулярній до площини.

Теорема (властивості перпендикуляра і похилої).

Якщо з точки, взятої поза площиною, проведені до площини перпендикуляр і похилі, то:

1. перпендикуляр коротший за будь-яку похилу;
2. проекції рівних похилих рівні і, навпаки, похилі, що мають рівні проекції, рівні;
3. з двох похилих більша та, проекція якої більша.

Теорема (про три перпендикуляри).

Якщо пряма, проведена на площині через основу похилої, перпендикулярна до її проекції, то вона перпендикулярна і до самої похилої.

Теорема (обернена до теореми про три перпендикуляри). Якщо пряма, проведена на площині через основу похилої, перпендикулярна до похилої, то вона перпендикулярна і до проекції похилої.

Теорема (про паралельні прямі та перпендикулярну площину).

Якщо площина перпендикулярна до однієї з двох паралельних прямих, то вона перпендикулярна і до другої.

Теорема (про паралельні площини та перпендикулярну пряму).

Якщо пряма перпендикулярна до однієї з паралельних площин, то вона перпендикулярна і до другої.

Кутом між площинами , які перетинаються, називається кут між прямими, проведеними в цих площинах зі спільної точки перпендикулярно до лінії їх перетину.

Дві площини називаються  перпендикулярними , якщо кут між ними дорівнює 90^о.

Теорема (ознака перпендикулярності площин).

Якщо площина проходить через пряму, перпендикулярну до другої площини, то ці площини перпендикулярні.

Теорема (властивість перпендикулярних площин).

Якщо дві площини перпендикулярні, то будь-яка пряма, що лежить в одній з них і перпендикулярна до прямої їх перетину, перпендикулярна до другої площини.

Відстанню між мимобіжними прямими  називається довжина їх спільного перпендикуляра.

Якщо пряма l  перпендикулярна  до  площини a , то таке проектування називають ортогональним або прямокутним.

Теорема (про площу ортогональної проекції многокутника).

Площа ортогональної проекції многокутника на площину дорівнює добутку його площі на косинус кута між площиною многокутника і площиною проекції.