Презентація "Прямокутна система координат у просторі"
Про матеріал
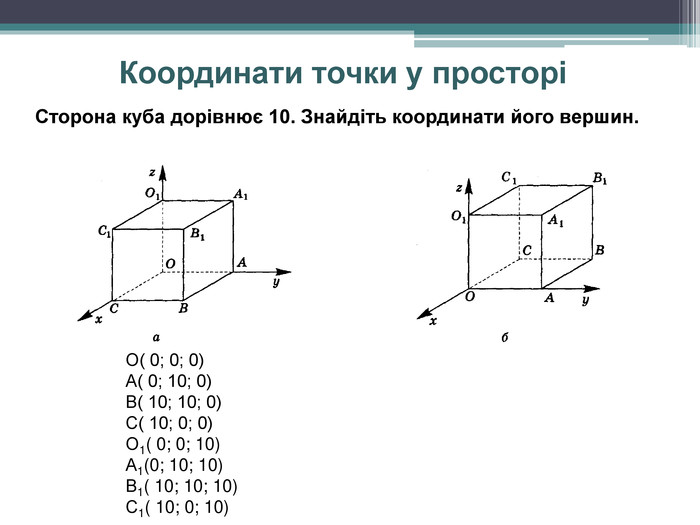
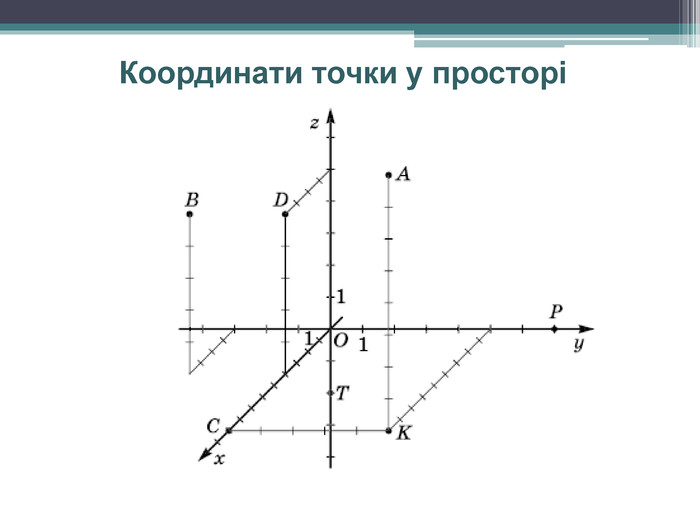
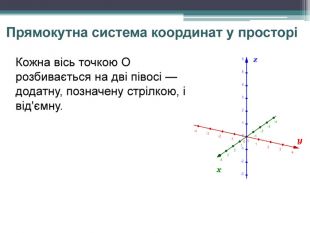
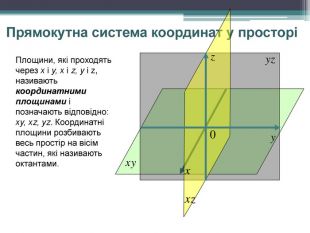
Презентація розроблена для наочного подання матеріалу з теми "Прямокутна система координат у просторі" Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку



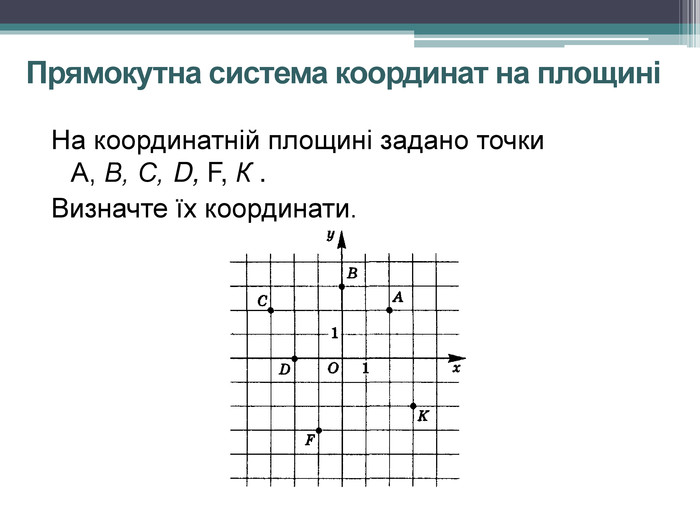


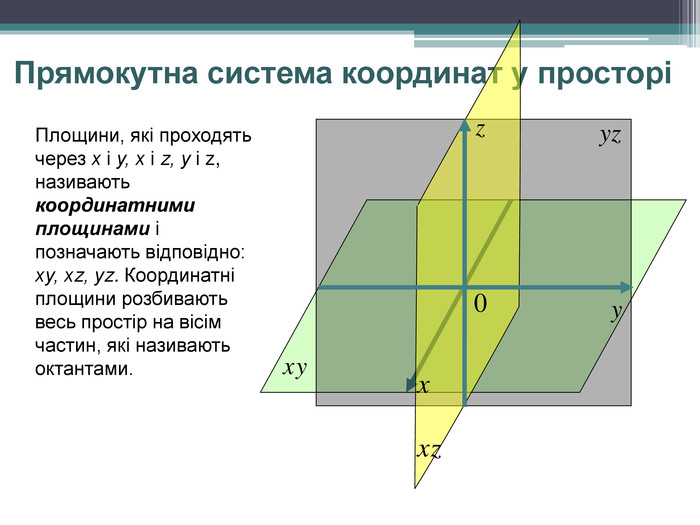
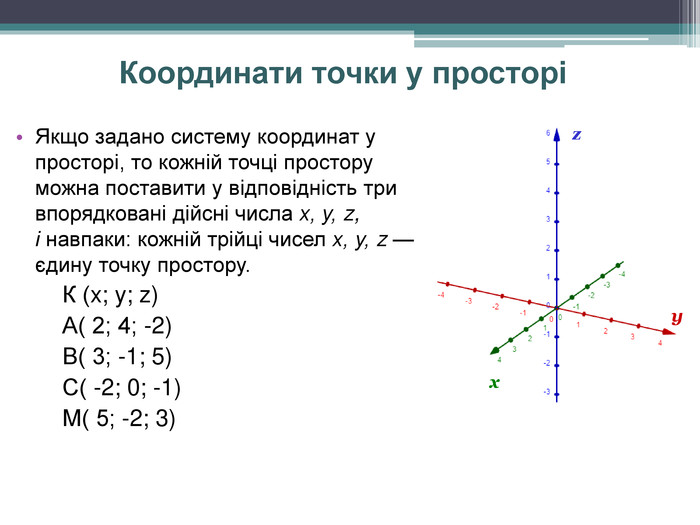

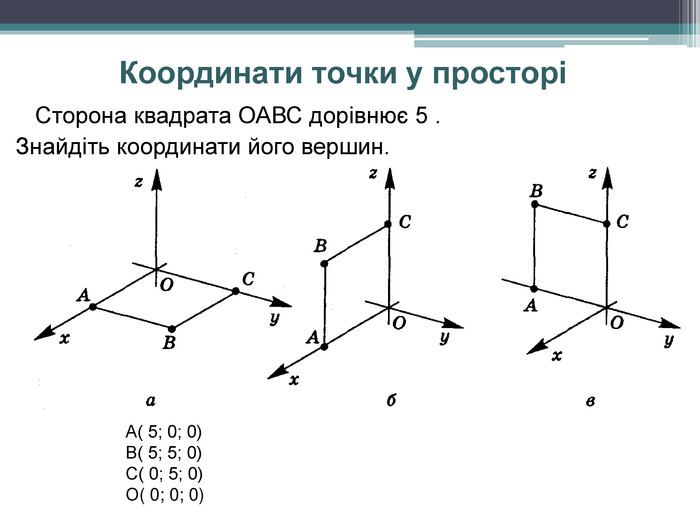












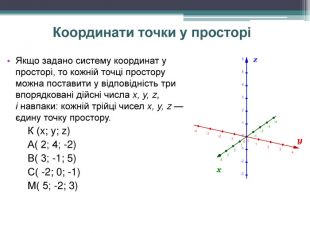

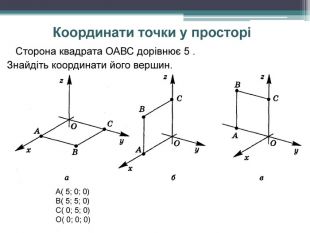
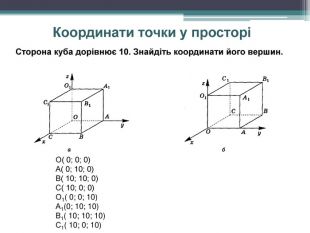









-

Мисік Марина Олександрівна
12.02.2025 в 11:25
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Куценко Людмила Михайлівна
13.12.2024 в 20:52
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Шумская Валентина
23.02.2024 в 13:05
Спасибі за розробку.
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Приходько Наталія Михайлівна
21.02.2024 в 12:45
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Почуєва Олена Анатоліївна
02.03.2023 в 18:54
Добрий вечір, колего!
Щиро дякую за розробку.
З повагою,Почуєва О.А.
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Худик Наталья
11.01.2023 в 14:12
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Савитская Ирина
04.09.2021 в 09:52
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 4 відгука