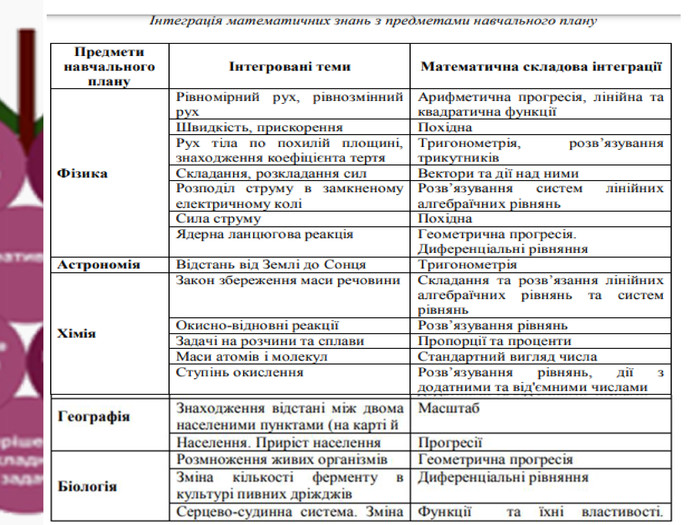
Інтеграція математичних знань з предметами шкільного курсу

Інтеграція математичних знань з предметами шкільного курсу. Вч. Ращупкіна Т. А.

Інтеграція навчальних предметів в різних країнах світу. У світовій практиці шкільництва є інтегрованій курс природничих наук Science (наука). Великій Британії відповідно до вимог програми «Природничі науки ХХІ століття» (Twenty First Сentury Science). Інтегрований курсу поділяється на: загальноосвітнього базового курсу природничих наук (GCSE Core Science), додатковий поглиблений (GCSE Additional General Science) та додатковий прикладний (GCSE Additional Applied Science). У Канаді природничі науки (інтегрованій в курс Science: фізика, хімія, біологія) вивчаються у початковій школі, а у старшій школі в 10 класі (Grade 10) «Наука» (Sciense - комплексний предмет, що включає вивчення хімії, фізики, біології) разом із математикою та англійською мовою входити до переліку трьох обов'язкових предметів.

Інтеграція –це…Інтеграція – це взаємопроникнення елементів, які є роз’єднані, але мають генетичну спорідненість: внутрішні зв’язки наук, мистецтв, знань та уявлень про світ та людину тощо. Педагогічна інтеграція – це доцільно організований зв’язок однотипних частин і елементів змісту, форм і методів навчання в рамках освітньої системи, що веде до розвитку особистості. Інтеграція математичних знань з предметами шкільного курсу –це «міжпредметні зв’язки математики».

Міжпредметні зв’язки математики з предметами шкільного курсу. Освітня функція міжпредметних зв’язків- це допомога вчителю математики формуєвати такі якості знань учнів, як системність, глибина, усвідомленість, гнучкість. У цьому випадку міжпредметні зв’язки виступають як засіб розвитку математичних понять, сприяють засвоєнню зв’язків між ними та загальними поняттями. Розвиваюча функція міжпредметних зв’язків- розвиток системного і творчого мислення учнів, формування їх пізнавальної активності, самостійності та інтересу до пізнання математики. Міжпредметні зв’язки допомагають подолати предметну інертність мислення і розширюють кругозір учнів. Виховна функція міжпредметних зв’язків-це забезпечення більш глибокого засвоєння знань, формування наукових понять і законів, наукового світогляду, а також покращення організації навчально-виховного процесу учнів, робить його більш оптимальним.

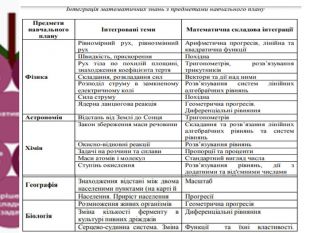
Неузгодженість програм природничо-математичних дисциплін{1 E171933-4619-4 E11-9 A3 F-F7608 DF75 F80}№Тема, математика, клас. Тема, предмет, клас1 Кут. Вимірювання кутів. 7 кл., І сем. Азимут. Географія, 6 кл., І семестр2 Координатна площина. 6кл., ІІ сем. Погода. Роза вітрів. Географія, 6 кл.Ісем.3 Відношення і пропорції. 6кл., І семестр(кінець)Масштаб. Географія, 6 кл., І семестр(початок)4 Вектори. Геометрія, 9 кл., І семестр. Взаємодія тіл. Сила. Фізика, 7 кл., ІІ семестр. Растрова графіка. Інформатика, 10 кл., І сем.5 Стандартний вигляд числа. Алгебра, 8 кл. Навколишній світ, в якому миживемо. Мікро-, макро- і мегасвіти. Фізика, 7 кл., І сем6 Пряма пропорційність. 7 клас., ІІ сем. Рівномірний прямолінійнийрух. Фізика, 8 кл., І сем.7 Показникова функція. 11 клас., І сем. Радіоактивність. Фізика, 9кл.,І семестр8 Похідна. Алгебра та початки аналізу, 10 клас., ІІ сем. Механічний рух. Фізика, 9кл., І семестр

Шляхи розв’язання проблеми узгодження програм. Ознайомлення з програмами з математики, хімії, біології, географії, природознавства. Установлення зв’язків між темами з шкільних предметів. Співпраця з вчителями природничо-математичних дисциплін. Спільне планування уроків. Взаємовідвідування уроків з цих предметів. Створення спільних позакласних заходів з предметів природничого циклу.

Математика і географія. Який шлях проходить за добу внаслідок обертання Землі місто Дрогобич, широта якого 49020’ ?Довжина паралелі 49020’ ≈ 29947,59 км. За годину ≈ 1247,816 км. За хвилину ≈ 2км. За секунду ≈347м

Математика і хімія. Математика-це інструмент рішення хімічних задач. Інтеграція математики з хімії це неформальний процес. Наприклад: Математичні рівняння і методи, використовувані в хімії, мають справу не з абстрактними величинами, а з конкретними властивостями атомів і молекул, які підпорядковуються природним обмеженням. Іноді ці обмеження бувають досить жорсткими і призводять до різкого звуження числа можливих рішень математичних рівнянь. Розглянемо рівняння 12x + y = 16. Для математика це рівняння описує пряму лінію на площині. Воно має нескінченно багато рішень, в тому числі і раціональних. Число атомів в молекулах має бути позитивним цілим числом. Тому для хіміка вираз 12x + y описує молекулярну масу вуглеводню Cx. Hy (12 - атомна маса вуглецю, 1 - водню). Молекулярну масу 16 має єдиний вуглеводень - метан, CH4, тому тільки одне рішення даного рівняння має хімічним змістом: x = 1, y = 4.

Математика і біологія. Кролики ФібоначчіУмови задачі: «В обгороджене місце поміщені пара кроликів (самка і самець) 1 січня. Ця пара кроликів починає приносити потомство через місяць, чи то пак з 1 лютого і дає приплід щомісяця по парі нових кроликів. Кожна нова пара кроликів стає статевозрілою рівно через місяць і теж починає приносити щомісяця по парі кроликів. Питання: скільки всього кролів буде через рік, чи то пак через 12 місяців з початку розмноження?»Розв’язок: Позначимо кількість пар кроликів через С, а через d — порядковий номер місяця. Складаємо формулу: Cd = Cd-1 + Cd-2— рекурентна формула. За допомогою отриманої формули розраховуємо кількість кроликів по місяцях1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233…Це так звані числа Фібоначчі — послідовність чисел, де кожне наступне число, починаючи з третього, виходить складанням двох попередніх чисел.

Математика і фізики. Світловідбивач. Катафот -Світловідбивач чи оптичний пристрій, що відбиває світло назад до джерела освітлення, незалежно від кута падіння променів на його поверхню. Ним оснащують усі транспортні засоби і небезпечні ділянки доріг. Катафоти виготовляють зі скла чи пластмаси. Катафот є побудованим з використанням властивостей  кутового відбивача.

Математика та неприродничі предмети «чим далі в ліс, тим більше дров»-зростання функції, «багато диму – мало тепла» - спадання функції, «не було ще ночі, якої не змінив світанок» - періодичність,«вище голови не стрибнеш» - обмеженість,  «ні риба, ні м'ясо» - функцію, що не є ані парною, ані непарною,«через вухналь (цвях) гублять підкову, через підкову – коня» - складену функцію,«і глибока криниця має дно» - функцію, що має границю, «дубовий гай вітру не боїться» - диференціювання функції у = ех. Вивчаючи окремі властивості функцій та фольклорний  опис:

Математика та християнська етика Проект «Ні дня без математики»

Математика формування підприємницької компетентності

Математика споживчих знань. Урок –екскурсія в супермаркет. Завдання: - здійснити закупку на 20 грн. - чек здати на аналіз вчителеві.

Робота над чеком з магазину «Рукавичка»Оглянути чек. Звернути увагу на вартість товару, знижка- 25%, сума до оплати. Чи виникли у вас питання до чисел: «сума знижки» «сума до оплати»?

Популяризація математики. Семінари. Учнівські конференціїМоделювання многогранни-ків Математичні ігри. Екскурсії Проєктна діяльність. Цікаві задачі

Задача про горизонт. R-радіус землі (64∙10⁵м)H-висота спостерігача (1,6м)d- відстань до горизонту. Теорема Піфагора. Яка відстань до лінії горизонту для спостерігача, що стоїть на Землі?

Математичні ігри. ОрігаміТанграм. ФлексагониІгри, що вчителі придумують згідно тем уроків: «математична пірамід», «лото дробових чисел», «вулик знань» тощо.«Великий квадрат не знає меж» (яп.пр.)

Впроваджування елементів STEM-освіти на уроках та у позакласній роботіМалювання сюжетів за допомогою многокутників. Моделювання многогранників. Виготовлення скриньок, моделей вуликів, медогонка, ялинкових прикрас і т.д. STEM проекти з електро конструктором. Прилад для демонстрування утворення фігур обертання. Виготовлення моделей автомобілів, зволожувача повітря, електроприлади тощо. Моделювання одягу

Тіла обертання навколо нас(Площі та об’єми тіл обертання)Круглі фрукти та овочіПосуд, як світ тіл обертання. Бублик-тор

Математика футбольного м’яча«Класичний» футбольний м'яч, Telstar  - усічений ікосаедр.«Сучасний» футбольний м’яч, Brazuca - куб.

Відкриті математичні питання. Нерозв'язані проблеми  — гіпотези, що видаються вірними, але дотепер не доведені. Проблеми Гільберта,Проблеми Ландау. Велика Теорема Ситника. Гіпотеза Гольдбаха і т.д. Задачі тисячоліття: Рівність класів P і NPГіпотеза Годжа Гіпотеза Рімана. Квантова теорія Янга — Мілса. Рівняння Нав'є — Стокса. Гіпотеза Берча і Свіннертона-Даєра

Задача «Про пакування куль» Задача на площині «доведено бджолами». Задача в трьох вимірному просторі (вивчали математика Томас Герріот  та астроном  Йоган Кеплер, 16ст.) доведнно Томасом Гейлсом у 1998році (шляхом перебору).2016 році -українка Марина В'язовська розв’язала задачу «Про пакування куль» для 8-вимірного простору (за це отримала премію Салема)Рішення, які запропонувала Марина, знаходять застосування в теорії текомунікацій, тобто написанні кодів для передачі сигналів для мобільного зв’язку, Інтернету чи космічних апаратів.

Досконале число — натуральне число, яке дорівнює сумі всіх своїх дільників, крім самого числа. Перші два досконалі числа були відомі ще в глибоку давнину. Найменшим досконалим числом є число 6: 6 = 3+2+1. Число відоме в Сародавній Греції: 6,28 Наступні два, а саме 496 і 8 128 -знайшов в IV столітті до н. е. Евклід 496 = 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248, 8 128 = 1 + 2 + 4 + 8 + 16 + 32 + 64 + 127 + 254 + 508 + 1016 + 2032 + 4064, 1460 р. було знайдене ще одне досконале число — 33 550 336. До середини XX ст. було знайдено ще 7 таких чисел. Кінець ХХст. обчислено ще 40 чисел; всього 47 чисел2013 року знайдено 48-е число : 257885161 – 1 – найбільше з відомих просте число Мерсенна. Починаючи з 1997 року їх пошуком займається команда розподілених обчислень з мережі Інтернет GIMPS. Досконалі числа

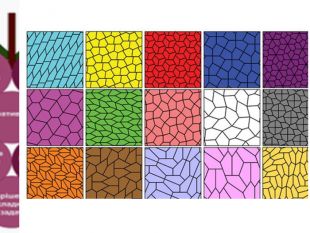
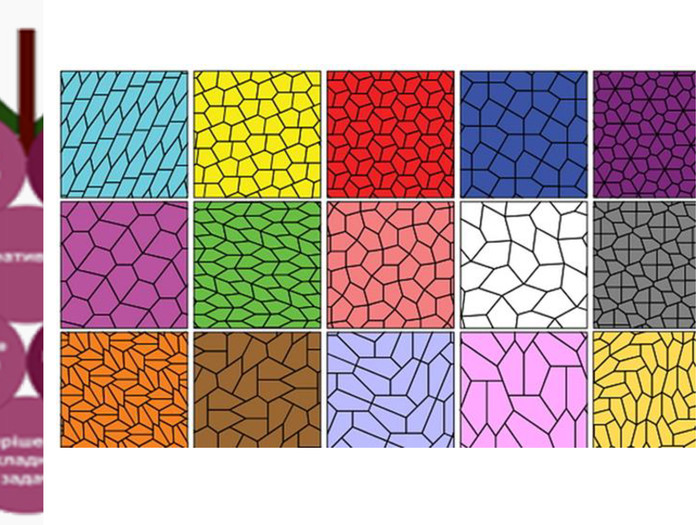
Теселяція п'ятикутниками. Теселяція-паркет, складений з кількох абсолютно однакових форм, які прилягають одна до одної без проміжків і не перекривають одна одну. Одне з перших вивчень теселяцій було зроблене в 1619  році Йоганном Кеплером, який описав правильні багатокутники на площині. Пошук п’ятикутників, якими можна замостити площину розпочався ще в 1918 році, коли німецький математик Карл Рейнхард виявив перші п’ять із них.1968 році Р. Б. Кершнер знайшов ще три, 1975 році Річард Джеймс довів їх кількість до дев’яти. 1976році Марджорі Райс, 50-річна домогосподарка із Сан-Дієго, розробила власний метод пошуку і за декілька років знайшла ще чотири. У 1985 році Рольф Штайн виявив чотирнадцятий п’ятикутник. 2016році група вчених із Вашингтонського університету — Кейсі Манн, Дженіфер Маклауд та Девід ван Деро — за допомогою комп’ютерного перебору великої кількості варіантів змогла знайти п’ятнадцятий п’ятикутник.

ПідсумокІнтеграція як ефективний педагогічний засіб має дві складові: внутрішню (можливості змісту самого предмету) і зовнішню(методичні прийоми вчителя, творчість та ентузіазм).Інтеграція для сучасної української освіти –одна з найважливіших та глобальних проблем, що потребує наукового осмислення, вивчення та узагальнення практичного досвіду.Інтеграція знань- інструмент створення передумов формування життєвих компетентностей.