Інтеграційно-компетентісний підхід до вивчення математики в школі
Департамент освіти і науки Одеської обласної державної адміністрації
Відділ освіти Балтської міської ради
НВК «Балтська загальноосвітня школа І-ІІІ ступенів №3-колегіум»
Н.С.Сєранова
Інтегративно-компетентісний підхід до викладання математики в основній та старшій
школі
Методичний посібник
для вчителів математики шкіл, гімназій, ліцеїв
Н.С.Сєранова
Інтегративно-компетентісний підхід до викладання математики в основній та старшій
школі
Методичний посібник
для вчителів математики шкіл, гімназій, ліцеїв
Балта 2020
У даному методичному посібнику розміщено матеріали, які допоможуть вчителям
математики в здійсненні компетентісного підходу до організації навчально-виховного процесу викладання математики, розкрито дидактичні можливості та методичні варіанти застосування інтеграції навчального матеріалу на уроках математики з метою підвищення якості математичної освіти, актуалізації пізнавальної активності учнів та підготовки до складання зовнішнього незалежного оцінювання .
Автор посібника:
Сєранова Наталія Сергіївна - вчитель вищої категорії НВК «Балтська ЗОШ І-ІІІ ст.
№3-колегіум», «старший вчитель»
Рецензенти:
Зміст
Вступ …………………………………………………………………………4
Розділ 1. Компетентність як педагогічне явище………………………7
1.1 Формування ключових компетентностей на уроках математики……… 1.2 Набуття учнями математичних компетентностей — одна з найважливіших складових життєвих компетентностей
Розділ 2. Методичні засади використання інтеграції навчального матеріалу на уроках математики при здійсненні компетентісного підходу
2.1 Методи навчання математики, що формують набуття математичних компетентностей
2.2 Інтеграція навчального матеріалу як засіб компетентісного підходу до викладання математики
2.2.1. Інтеграція навчального матеріалу в межах одного предмета
2.2.2. Міжпредметна інтеграція навчального матеріалу на уроках
математики
2.3 Застосування компетентісних задач на ЗНО
Висновки……………………………………………………...42
Додатки…………………………………………………….....44
Список літератури………………………………………………………65
ВСТУП
Перед сучасною школою постала необхідність формування нового типу мислення, нової свідомості, нового розуміння людиною свого місця в суспільстві та житті.
Освіта повинна забезпечити молоду людину не тільки системою знань та навчальних навичок, а, насамперед, вмінням здобувати самостійно ці знання, володіти інформаційною культурою, мати навички соціальної адаптації.
Саме ці пріоритети лежать в основі реформування сучасної загальноосвітньої школи, головне завдання якої — підготувати компетентну особистість, здатну знаходити правильні рішення у конкретних навчальних, життєвих, а в майбутньому і професійних ситуаціях. Тому актуальним завданням сучасної школи є реалізація компетентнісного підходу в навчанні, який передбачає спрямованість освітнього процесу на формування і розвиток ключових компетенцій особистості. Результатом такого процесу має бути сформованість загальної компетентності людини, яка включає сукупність ключових компетенцій і є інтегрованою характеристикою особистості.
Актуальність розробки
Впровадження компетентнісного підходу у школі є одним із важливих концептуальних положень оновлення змісту та якості освіти. Сучасний навчальний заклад має сприяти розвиткові демократичної культури, формуванню, необхідних для проживання у європейському співтоваристві компетентностей, політико-правових і соціально-економічних знань. Важливим нині є не тільки об’єм знань, а й уміння ними оперувати, бути готовим змінюватись та пристосовуватись до нових потреб ринку праці, оперувати й управляти інформацією, активно діяти, швидко приймати рішення, навчатись упродовж життя. Прогресивна освітня спільнота сьогодні ставить перед собою нове завдання – сформувати у школяра та дорослої людини вміння вчитися. Це вміння формується шляхом компетентнісно-орієнтованого підходу до навчання.
Формування математичної компетентності учня на сьогоднішній день є однією із актуальних проблем освіти і може розглядатися як вихід із проблемної ситуації, що виникла через протиріччя між необхідністю забезпечити якість освіти та неможливістю вирішити цю проблему традиційним шляхом.
Компетентнісно-орієнтовані завдання забезпечуватимуть учня не відокремленими предметними знаннями, а допоможуть сформувати цілісне уявлення про світ, де важливо вміти застосовувати ті чи інші знання, навчати дитину здобувати ці знання і, в першу чергу, мотивувати на отримання нових знань.
Практична значущість досвіду
У сучасних умовах учень повинен отримати в школі те, що допоможе йому утвердитися в житті: моральне ставлення до себе і людей, усвідомлення своїх громадянських почуттів, ключові компетентності, що дозволяють успішно функціонувати в будь-якій сфері діяльності. Тому, в даний час перед школою поставлені завдання: формування навчального середовища, яке мотивує учнів самостійно здобувати, обробляти отриману інформацію, швидко орієнтуватися в інформаційному просторі; створення умов, що сприяють розвитку ключових компетенцій. Саме розвиток в особистості життєво важливих компетентностей може дати людині можливості орієнтуватись у сучасному суспільстві, інформаційному просторі, швидкоплинному розвиткові ринку праці, подальшому здобутті освіти.
Одним із головних завдань вчителя є зміна організації традиційного уроку, включення спеціально організованої діяльності учнів в освітній процес на основі використання компетентнісно-орієнтованих завдань.
Для нашого часу характерна інтеграція наук, прагнення отримати якомога більш точне уявлення про загальну картину світу. Ці ідеї знаходять відображення в концепції сучасної шкільної освіти. Але вирішити таке завдання не можливо в рамках одного навчального предмета, Тому в теорії та практиці навчання спостерігається тенденція до інтеграції навчальних дисциплін, яка дозволяє учням досягати міжпредметних узагальнень і кращого засвоєння навчального матеріалу. Це особливо важливо для викладання математики, методи якої використовуються у багатьох галузях знань і людської діяльності. Проблемами інтеграції навчальних дисциплін на рівні загальноосвітньої школи займається ряд вітчизняних науковців серед яких варто виділити Н.Бібік, О.Комар, О.Нудельмана, О.Пометун. В роботі визначено основні напрямки інтеграції в сучасній школі, розкрито деякі аспекти інтеграції математики з предметами природничо-математичного циклу, доведено доцільність проведення інтегрованих уроків та їх результативність, а також запропонувати зразки застосування прикладних задач. Математика специфічний предмет, який вимагає формування стійких умінь та навичок виконання певних дій і алгоритмів, що потребує виконання багатьох тренувальних вправ. Тому важливим є напрацювання кожним вчителем власної методики роботи з обдарованими дітьми на кожному «стандартному» уроці. Безумовним є те, що вчитель не може орієнтуватись ні на середнього ,а ні на сильного учня. Він має орієнтуватися на кожного учня. В цьому саме і полягає суть особистісно орієнтованого навчання.
З огляду на досвід роботи можу зазначити, що найважливішим є створення емоційно актуального фону не тільки і не стільки окремого уроку, а навчання в цілому. Необхідно вибудувати таку систему взаємин між вчителем і окремим учнем і між вчителем і учнівським колективом, в якій кожен учень почувався б вільно і спокійно, а клас в цілому був працездатним і високоорганізованим до співпраці з учителем, до здобуття знань, до усвідомлення необхідності навчання. Створення такого освітнього простору є дуже важливим і важким завданням для вчителя.
РОЗДІЛ 1
Компетентність як педагогічне явище
Реформування системи освіти в Україні набуло нині глобального характеру. Ми є свідками і учасниками процесів, котрі безпосередньо пов'язані з реформуванням змісту освіти затвердження Державних стандартів початкової освіти та базової середньої освіти. Результатами навчання в цій системі визнаються рівень навчальних досягнень та компетенції учнів. "Компетенції є інтегрованим результатом навчальної діяльності учнів...". Чим обумовлена перспективність такого результату? "Визначення навчальних досягнень учнів є особливо важливим з огляду на те, що навчальна діяльність у кінцевому підсумку повинна не просто дати людині суму знань, умінь та навичок, а сформувати її компетенції".
1.1 Формування ключових компетентностей на уроках математики
Формування компетентностей учнів зумовлене не тільки реалізацією відповідного оновлення змісту освіти , а й адекватних методів та технологій навчання. Але зміст та методика викладання будь-якого предмета мають певні специфічні риси стосовно формування компетентностей учнів .
Ось характеристика предметного арсеналу шодо формування компетентностей
учителями математики.
Соціальна компетентність.
● Вибір учителем завдань , які передбачають для учнів самостійний пошук розв'язку.
● Надання учням можливості обрання варіанту завдання чи шляху розв'язання задач.
● Використання самооцінки та взаємооцінки учнів.
● Розв’язування задач різними способами та визначення раціонального шляху розв'язування.
● Залучення дітей до роботи в групах. Обов'язкова умова- врахування індивідуальних можливостей школярів. Завдання мають бути якщо не індивідуальними, то хоча б різнорівневими .
● Надання учням можливості виявлення ініціативи.
● Практикування доручень учням ( наприклад : „ відповідальний за наочність” , „ консультант ” тощо .
● Планування виховних заходів та заходів предметних тижнів, у яких передбачається самостійна активна діяльність учнів .
● Залучення дітей до самоврядування .
Полікультурна компетентність.
● Використання інформації з історії математичних відкриттів.
● Використання художньої літератури в процесі викладання математики.
● Розв'язання задач історико-культурного змісту.
● Розв'язання задач екологічного змісту .
● Характеристика внеску в науку вчених різних національностей.
● Наголошення на внеску в розвиток науки українських математеків.
● Виховання учнів на прикладі життєвого та творчого шляху видатних математиків.
Комунікативна компетентність.
● Стимулювання вміння учнів висловлювати власну точку зору.
● Сприяння удосконаленню вмінь вести навчальний діалог.
● Використання усних та письмових рецензій на відповідь, доповнень та зауважень до неї .
● Удосконалення вмінь дітей формулювати цілі власної діяльності та робити висновки за її результатами.
● Застосування взаємоопитування та взаємоперевірки з можливим подальшим коментуванням.
● Організація групової роботи .
● Проведення нестандартних уроків , уроків-змагань , КВК.
● Підготовка учнями нестандартних запитань однокласникам .
● Стимулювання спілкування учнів з ровесниками та дорослими з метою підвищення рівня навчальних досягнень та ерудиції учнів.
Інформаційна компетентність.
● Залучення вчителем додаткової інформації в процесі викладання математики. ● Стимулювання учнів до використання додаткової інформації.
● Активна співпраця з кабінетом інформатики щодо використання навчальних програм з математики.
● Використання малюнків , таблиць , схем , як джерел інформації, та передбачення складання схем , таблиць , планів , опорних конспектів , як результату роботи учнів з інформацією.
● Випуск шкільних газет , створення інформаційних сторінок у класних куточках.
Компетентність самоосвіти і саморозвитку.
● Написання учнями повідомлень , рефератів , самостійних творчих робіт.
● Використання випереджальних завдань , що передбачають активну самостійну та самоосвітню діяльність учнів.
● Залучення учнів до творчих виставок .
● Залучення учнів до роботи в МАН.
● Консультування учнів з питань самоосвіти .
● Організація інтелектуальних конкурсів , ігор , предметних тижнів, які передбачають самостійне опанування учнями певних питань та їх самоосвітню діяльність.
● Використання інтенсивних завдань з предмету , які передбачають пояснення учнями певних питань.
● Використання навчальних програм з метою самоосвіти учнів.
● Залучення учнів до роботи консультантами , що підтримує їх самоосвітній тонус.
Компетентність продуктивної творчої діяльності.
● Забезпечення високого наукового рівня викладання математики .
● Створення проблемних ситуацій на основі сучасного життя .
● Розв'язування задач та прикладів різними способами , використання задач підвищеної складності.
● Складання та розв'язування учнями тестів , задач , кросвордів тощо.
● Залучення учнів до участі в конкурсах „ Кенгуру " ,„ Золотий ключик " тощо. Залучення учнів до участі в олімпіадах , МАН , у роботі заочних фізико-математичних шкіл.
Математика не існує у безповітряному просторі, математичні поняття, аксіоми, теореми мають своїм витоком реальність і своєю метою мають дослідження реальності за допомогою математичного моделювання.
Викладання математики має відбивати діалектику пізнання дійсності і побудови самих математичних теорій на основі практики.
Саме тому свою роботу вчитель математики здійснює відповідно до вимог сьогодення, тому актуальним буде формування математичних компетентностей школярів на основі принципів історизму та прикладної спрямованості.
Головне завдання вчителя — розвиток здібностей і навичок учнів, підвищення престижу знань, формування математичних компетентностей, вміле використання випускниками школи набутих у процесі навчання вмінь і практичних навичок у повсякденному житті. Вчитель повинен знайти шлях до особистості учнів через звернення до їх життєвого досвіду, через підбір задач прикладного змісту (Додаток 1), через використання історичного матеріалу, що викликає інтерес учнів до предмета, формує у них певні компетентності.
1.2 Набуття учнями математичних компетентностей — одна з найважливіших складових життєвих компетентностей
Математична освіта покликана зробити вагомий внесок у формування ключових компетентностей учнів як загальних цінностей, що базуються на знаннях, досвіді, здібностях, набутих завдяки навчанню. Отримані у школі знання та сформовані вміння і навички є, безперечно, важливими, але нині особливої актуальності набуває компетентність учня в різних галузях знань. Саме компетентності більшість міжнародних експертів вважають тими індикаторами, що дають змогу визначити готовність учнявипускника до життя, подальшого особистого розвитку та активної участі в суспільному житті.
З точки зору компетентнісно зорієнтованого підходу до організації навчально-виховного процесу, зміст математичної освіти має бути спрямований на досягнення таких цілей:
• інтелектуальний розвиток учнів, формування видів мислення, характерних для
математичної діяльності і необхідних людині для повноцінного життя у суспільстві;
• оволодіння прийомами математичної діяльності, які необхідні у вивченні суміжних предметів для продовження навчання та у практичній діяльності;
• формування уявлень про математику як форму опису і метод пізнання дійсності;
• виховання учнів у процесі навчання математики;
• формування позитивного ставлення та інтересу до математики.
Викладання математики має відображати діалектику пізнання дійсності і побудови математичних теорій. Саме практичній і творчій складовій навчальної діяльності приділяють особливу увагу в Державному стандарті.
Математичні компетентності складають основу для формування ключових компетентностей. За визначенням С. А. Ракова, математична компетентність — це спроможність особистості бачити та застосовувати математику в реальному житті, розуміти зміст і метод математичного моделювання, будувати математичну модель, досліджувати її методами математики, інтерпретувати отримані результати, оцінювати похибку обчислень.
Для успішної участі у сучасному суспільному житті особистість повинна володіти певними прийомами математичної діяльності і навичками їх застосувань до розв’язування практичних задач. Значні вимоги до шкільної математичної освіти у розв’язанні практичних задач ставлять сучасний ринок праці, отримання якісної професійної освіти, продовження освіти на наступних етапах. Тому одним із головних завдань навчання математики є забезпечення умов для досягнення кожним учнем математичної компетентності.
Математична компетентність — це вміння бачити та застосовувати математику в реальному житті, розуміти зміст і метод математичного моделювання, вміння будувати математичну модель, досліджувати її методами математики, інтерпретувати отримані результати, оцінювати похибку обчислень.
Напрями набуття математичної компетентності
Будувати і досліджувати найпростіші математичні моделі реальних об’єктів, процесів і явищ.
Володіти необхідною оперативною інформацією для розуміння постановки математичної задачі.
Володіти технікою обчислень.
Уміти проектувати і здійснювати алгоритмічну та евристичну діяльність на математичному матеріалі.
Уміти працювати з формулами.
Уміти будувати і читати графіки функціональних залежностей, досліджувати їхні властивості.
Уміти класифікувати і конструювати геометричні фігури на площині і у просторі.
Уміти оцінювати шанси настання тих чи інших подій, міру ризику під час того чи іншого рішення, обирати оптимальний варіант.
Математична компетентність є важливим показником якості математичної освіти, природничої підготовки молоді.
Процес обговорення математичних компетентностей буде незавершений, якщо не обговорити методи навчання, які сприяють набуттю математичних компетентностей у процесі навчання, якщо не обговорити критерії набуття математичних компетентностей та засобів вимірювання їх рівня набуття.
РОЗДІЛ 2.
Методичні засади використання інтеграції навчального матеріалу на уроках математики як засобу формування ключових компетентностей учнів
2.1 Методи навчання математики, що формують набуття математичних
компетентностей
Методи навчання математики істотно відрізняються від методів навчання, наприклад, історії, біології, іноземної мови. Розробити оптимальну теорію методів навчання для всіх шкільних предметів навряд чи можливо. Розглянемо найважливіші методи навчання математики в сучасній середній загальноосвітній школі.
Активні методи навчання
• Метод конкретної ситуації (вчить школярів думати, узагальнювати, аналізувати, розглядати різні варіанти, складати свої задачі. Доцільніше розібрати кілька способів розв’язання однієї задачі, ніж кілька схожих задач).
• Метод інциденту (залучення учнів до участі в олімпіадах, у міжнародній грі «Кенгуру». Учні вчаться долати інертність, переборювати стресові ситуації, що так важливо у житті).
• Метод мозкового штурму (привчає учнів на поставлені запитання давати свої варіанти відповідей).
• Метод занурення (створюються ситуації, де учні з головою занурюються в поставлені завдання, ефективно розв’язують їх).
• Метод евристичних питань (спонукає учнів думати, аналізувати).
• Кооперативний метод (використовується при роботі в групах).
• Дослідницький метод
• Метод проектів
Метод проектів — це освітня технологія, яка націлена на придбання учнями знань.
Метод проектів стимулює учнів до розв’язання проблем; розвиває критичне мислення; учні набувають навичок роботи з інформацією; вчаться вирішувати пізнавальні, творчі завдання у співробітництві.
Проектна діяльність відкриває в учнях лідерів, які уміють організовувати роботу в своїх групах. Розвивається вміння співпрацювати, відчути себе членом команди, брати відповідальність на себе, формується комунікативна компетентність.
Важливе завдання процесу навчання математики в школі — домогтися глибокого і міцного засвоєння учнями теоретичних знань: математичних понять, тверджень про їхні властивості (аксіоми, теореми), правил, законів; сформувати навички й уміння застосування теоретичних знань на практиці і оволодіння способами творчої діяльності, досягти глибокого усвідомлення учнями світоглядних і морально-етичних ідей. Слід розрізняти поняття «процес навчання» і «процес одержання освіти». Для того, щоб людина була освіченою у повному розумінні слова, потрібні три властивості: широкі знання, звичка мислити, шляхетність почуттів. Процес навчання — двосторонній процес взаємодії між тим, хто вчить, і тим, хто навчається. Закономірності процесу навчання, що об’єктивно існують, виступають як основні вимоги до практичної організації навчального процесу. Вони дістали назву дидактичних принципів. Дидактичні принципи організації навчального процесу
• Науковість і ідейно-політична спрямованість.
• Проблемність.
• Наочність.
• Активність і свідомість.
• Доступність.
• Систематичність і послідовність.
• Міцність.
• Єдність освіти, розвитку і виховання.
Провідна роль теоретичних знань. У процесі навчання математики це означає, що не можна починати формувати уміння і навички застосування математичних знань доти, поки учні не засвоїли основні поняття, твердження, правила, закони, методи.
Навчання швидкими темпами. У досвіді вчителів-новаторів (В. Ф. Шаталова, Р. Г. Хазанкіна та ін.) реалізація цього принципу зводиться до вивчення основного теоретичного матеріалу швидкими темпами на початку ознайомлення з темою, здійснення дійового контролю його засвоєння і звільнення цим самим часу для розв’язування задач. У процесі розв’язування задач теоретичний матеріал повторюється, поглиблюється, закріплюється.
Навчання на високому, але доступному рівні складності. Так само, як спортсмени розвивають свої фізичні можливості на вправах високої складності, учні повинні розвивати мислення, інтелект на навчальних задачах високого рівня складності. Цього принципу стосуються введені ще в 30-х pp. XX ст. психологом JI. С. Виготським поняття зони актуального і зони найближчого розвитку учнів. Учень працює в зоні актуального розвитку тоді, коли розв’язує навчальні задачі в межах засвоєного ним навчального матеріалу. Проте, як зазначав JI. С. Виготський, треба працювати на завтрашній день учня, тобто працювати в зоні його найближчого розвитку. Це означає, що учень має працювати над навчальними задачами, які він ще не спроможний розв’язати самостійно, але за незначної допомоги вчителя або своїх товаришів він таким задачам дає раду. Так, наприклад, під час вивчення теми «Звичайні дроби» можна запропонувати учням стати редакторами нового міні-підручника (Додаток 3), що дозволить формувати нові навички та компетентності. Разом з тим об’єктивним фактором є те, що різні учні мають різні зони актуального і найближчого розвитку. Саме тому в умовах класно-урочної системи треба здійснювати рівневу диференціацію, використовувати групові й індивідуальні форми роботи, виділяючи типологічні групи учнів, які мають приблизно однаковий рівень загального розвитку, навченості, темпу просування у навчанні, інтересу до математики. В умовах класно-урочистої системи навчання рівнева диференціація постає ефективним засобом формування в учнів самооцінки та самоконтролю.
2.2 Інтеграція навчального матеріалу як засіб компетентісного підходу до викладання математики
2.2.1. Інтеграція навчального матеріалу в межах одного предмета
Забезпечення прикладної спрямованості викладання математики сприяє формуванню стійких мотивів до навчання взагалі і до навчання математики зокрема. Реалізація у навчанні прикладної спрямованості навчання математики означає:
1) створення запасу математичних моделей, які описують реальні явища і процеси, мають загальнокультурну значущість, а також вивчаються у суміжних предметах;
2) формування в учнів знань та вмінь, які необхідні для дослідження цих математичних моделей;
3) навчання учнів побудові і дослідженню найпростіших мате матичних моделей реальних явищ і процесів.
Одним з ефективних засобів формування вмінь є ІНТЕГРАЦІЯ НАВЧАЛЬНОГО МАТЕРІАЛУ, яка здійснюється, наприклад, при вивченні етюдів, побудованих на геометричному матеріалі.
Етюди шкільного курсу геометрії - це невеликі за обсягом, логічно завершені фрагменти теорії з окремих питань. Вони містять геометричні твердження і зв’язки між ними, які учні повинні знати і вміти застосовувати до розв'язування задач. При такому підході зменшується обсяг інформації, яку потрібно запам'ятати учневі; покращується взаємозв'язок теоретичного і задачного матеріалу, оскільки багато теоретичних відомостей учні засвоюють розв'язуючи задачі, досліджуючи здобуті результати учнів ефективно формуються вміння розв'язувати складні задачі. Гарні можливості для складання етюдів дає такий геометричний матеріал:
- кола, дотичні і січні;
- висоти, бісектриси і медіани в трикутниках;
- прямокутні трикутники; - трапеція:
а) довільна трапеція;
б) довільна трапеція, в яку вписане коло;
в) рівнобічна трапеція;
г) рівнобічна трапеція, в яку вписане коло;
д) рівнобічна трапеція, в яку вписане коло і діагоналі перпендикулярні до бічних сторін;
- площі геометричних фігур.
Спочатку вивчаються опорні поняття і теореми, деякі визначні метричні теореми (геометричну азбуку), а потім - етюди геометрії. Учні аналізуючи відповідні конфігурації фігур в етюдах, досліджують зв'язки між твердженнями. Поступово, у міру вивчення навчального матеріалу, з'ясовуються нові твердження, поглиблюються і систематизуються зв'язки між ними. Далі розв'язуються складні задачі. Тому основний метод навчання -проблемно-пошуковий.
Важливе значення при вивченні геометричних етюдів мають рисунки, оскільки відшукання нових зв'язків, "відкриття" геометричних закономірностей покращується, якщо в учнів вироблено вміння аналізувати рисунки, правильно інтерпретувати їх наочний зміст. Крім того, вдало виконаний рисунок до задачі допомагає знайти ідею розв'язання, навести на думку використати певну теорему або виконати додаткову побудову, відшукати раціональний спосіб розв'язання.
Ця методика передбачає виділення типових конфігурацій фігур в курсі геометрії і їх узагальнення в міру вивчення навчального матеріалу. Таким чином, одержується можливість розв'язувати різні складні задачі за одними і тими ж конфігураціями фігур і виявляти, тим самим, спільні підходи до їх розв'язання.
Вивчення етюдів геометрії сприяє формуванню науково-теоретичного мислення учнів. Справді, вивчаючи геометрію логічно завершеними порціями, учні вчаться виділяти провідні поняття, принципи, ідеї спочатку для певної порції навчального матеріалу, а потім переносити їх на інший матеріал і узагальнювати.
При інтеграції навчального матеріалу за допомогою етюдів, використовується також і паралельне структуювання навчального матеріалу.
Використовується також аналогія у формулюванні і при розв'язуванні деяких задач. Чи дає можливість об'єднувати задачі і розв'язувати їх паралельно. Паралельне структуювання навчального матеріалу покращує вироблення геометричних умінь учнів, дає можливість економити навчальний час.
Застосування етюдів для інтеграції навчального матеріалу дозволяє поглибити знання та уміння учнів.
Дійсно, передбачається завершення вивчення кожної теми навчальним матеріалом, який її поглиблює. Це може бути як теоретичний матеріал, так і його практичне застосування. Тобто включаються невеликі фрагменти теорії, які дають можливість розглянути змістовні, красиві задачі. Наприклад, тема "Чотирикутники" завершується вивченням етюду про визначні точки і лінії у трикутниках (центр мас і ортоцентр трикутника, точки і коло Ейлера), тему "Координати на площині" - етюдом про еліпси, параболи та гіперболи, їх властивості.
Інтеграція навчального матеріалу посилює внутріпредметні і між предметні зв'язки, що також сприяє глибшому засвоєнню понять і теорем. Це насамперед зв'язки між окремими поняттями, теоремами між планіметрією і стереометрією. Використовуються спільні підходи до доведення теорем і розв'язування задач, аналогія між геометричними фактами.
Розглянемо приклад геометричного етюду :
"РІВНОБІЧНА ТРАПЕЦІЯ, В ЯКУ ВПИСАНО КОЛО".
Нехай у рівнобічну трапецію АВСД вписано коло з центром О1 і радіусом r (рис.1 ); X, У - точки дотику кола до основ трапеції; Т, R - до бічних сторін; МН - середня лінія; BL ⊥ AD.
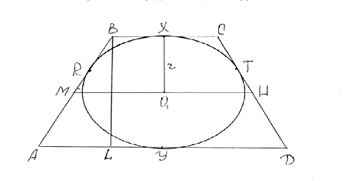
Рис.1
Точка перетину діагоналей трапеції ділить висоту XY у відношенні 𝑏 , починаючи від верхньої основи. Учні ,що навчаються на високому рівні,𝑎
досліджують зв’язки між площинами трикутника та трапеції.
Позначимо 𝑆𝐵𝑂1𝐶 = 𝑆𝑏 * 𝑆𝐴𝑂𝐷 = 𝑆𝑎 * 𝑆𝐵𝑜𝑐 = S 1 * 𝑆𝐴𝑂𝐷 = S2 , а 𝑆𝐴𝐵𝐶𝐷 = 𝑆.
Тоді Sa = 12 𝑆 * 𝑆2 Sb = 12 𝑆 * 𝑆1
Доведемо ці рівності.
Трикутники AO1D і DOA мають рівні висоти, тому 𝑆𝑎𝑆𝑏 = 𝑏𝑎 .
∆ ~ ∆𝐷𝑂𝐴 З подібності трикутників BOC випливає:
√√𝑆𝑆21 = 𝑎𝑏 .
Отже, 𝑆𝑎𝑆𝑏 = √√𝑆𝑆21 , або Sb = Sa* √ 𝑆𝑆12 . Знаходимо
Sa + Sb = 12 ar + 12 br = 12 r (a + b) = 21 h ( 𝑎+2𝑏 ) = 12 S.
Оскільки S= ( 𝑆1 + √𝑆2)2 , то Sa + Sb = 12 ( 𝑆1 + √𝑆2)2 .
Тоді , підставивши у ліву частину даної рівності вираз для S, дістанемо Sa (1-√ 𝑆1 ) = 12 ( 𝑆1 + √𝑆2)2 , або Sa 𝑆√1 +𝑆2√𝑆2 = 21( 𝑆1 + √𝑆2)2.
𝑆2
Звідси Sa= 12 √𝑆2( 𝑆1 + √𝑆2) = 12 √𝑆2*S. Аналогічно доводимо рівність
Sb = 12 √𝑆1*S.
Розглянемо ще один з можливих варіантів геометричного етюду на тему:
"КОЛО, ВЛАСТИВОСТІ ЙОГО СІЧНИХ ТА ДОТИЧНИХ".
Дано кола з центрами О і О1 й радіусами R та r, причому R ˃ r (рис. 2 ).
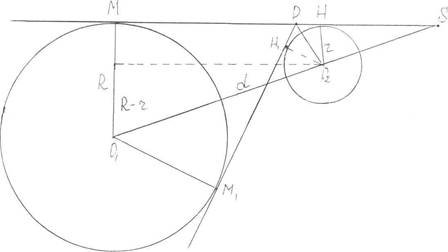
Рис. 2
Проведемо спільну зовнішню дотичну до цих кіл з точкам дотику М і Н. Точку перетину лінії центрів з цією дотичною позначимо S. Нехай O1O2=d, тоді
МН= 𝑑2 − (𝑅 − 𝑟)2 (за теоремою Піфагора з трикутника О1КО2).
Оскільки О1М⊥М𝐻, О2𝐻⊥М𝐻, то ∆𝑆𝐻𝑂2~∆𝑀𝑂1𝑆. Отже,
𝑅𝑟 ≡ 𝑆𝑀𝑆𝐻 = 𝑆𝑆𝑂𝑂21 , SM=SH+MH, a SO1= SO2+O1O2= SO2+d.
Звідси можна знайти відрізки SH та SO2.
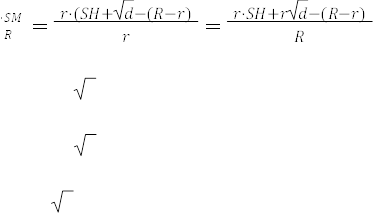SH= 𝑟. Тому
R* SH=r* SH+ 𝑟 𝑑 − (𝑅 − 𝑟)
R* SH- r* SH= 𝑟 𝑑 − (𝑅 − 𝑟) SH*(R-r) = 𝑟 𝑑 − (𝑅 − 𝑟)∆
SH = 𝑟 𝑑𝑅−−(𝑅𝑟−𝑟) .
Піднесемо обидві частини до квадрата і одержимо: SH2 =( 𝑟𝑑𝑅−−(𝑅𝑟−𝑟) )2. Маємо:
SH
SH =
.
Знайдемо so2 з рівності:
𝑆𝑂𝑆𝑂2 = 𝑅𝑟 , 𝑆𝑂𝑆𝑂1+2𝑑 = 𝑅𝑟 , SO2 = 𝑟(𝑆𝑂𝑅2+𝑑) , SO2 = 𝑟𝑆𝑂𝑅2+𝑟𝑑 .
1
Отож з даних перетворень видно, що відстань від точки S до центра кола можна виразити як SO2 = 𝑟𝑆𝑂2+𝑟𝑑 . RSO2 = rSO2+𝑅rd
RSO2- rSO2= rd
SO2(R-r) = rd
SO2= 𝑅𝑟𝑑−𝑟
Якщо провести спільну внутрішню дотичну з точками дотику М1 та Н1, то
M1H1 = R1O2= 𝑑2 − (𝑅 + 𝑟)2
Точка Р – точка перетину зовнішньої та внутрішньої дотичних. Тоді PO1 та PO2 бісектриси кутів MPM1 і HPH1 , відповідно. Отже сума кутів O1PH1 + O2PH1=180°/2=90°.
Тоді O PO - прямокутний і .
∆ 1 2 ∆𝑂1𝑀𝑃~∆𝑃𝐻𝑂2
Якщо коло з центром в точці O2 паралельно перенесемо на вектор а
, то дані кола будуть дотикатися в М2
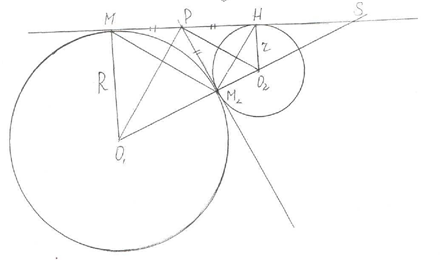
Рис.3
Очевидно внутрішня дотична займе місце спільної дотичної до обох кіл. Нехай X - довільна точка спільної дотичної РМ2 . Тоді ХУ= XZ, де ХУ і ХZдотичні до даних кіл, проведені з точки X.
Корисним при розв'язуванні задач є таке твердження:
Пряма М Н (М1- точка, симетрична точці М відносно О1 ) проходить через точку М2 дотику цих кіл.
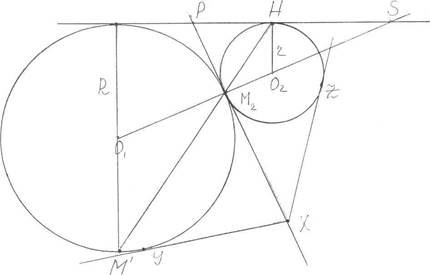
Рис.4
Довести дане твердження можна методом від супротивного, доповнивши рисунок додатковою побудовою.
Аналогічно вивчається і інший геометричний матеріал. Здібні з математики учні більш глибоко досліджують зв'язки в етюдах. Тим самим, забезпечується диференційований підхід до навчання геометрії.
2.2.2. Міжпредметна інтеграція навчального матеріалу на уроках математики
Пошуки ефективних шляхів підвищення виховного рівня процесу навчання в школі все більше привертають увагу педагогів, вчених і практиків до проблеми міжпредметних зв'язків. У дослідженнях відомих вчених-педагогів (І. Д. Звєрєва, В. М. Коротова, М. М. Скаткін та ін) міжпредметні зв'язки виступають як умова єдності навчання і виховання, засіб комплексного підходу до предметної системи навчання. Проблема міжпредметних зв'язків цікавила педагогів ще в далекому минулому. Прогресивні педагоги - Я.А. Коменський, К.Д. Ушинський,- підкреслювали необхідність взаємозв'язків між навчальними предметами для відображення цілісної картини природи «в голові учня», для створення істинної системи знань і правильного світорозуміння. Актуальність міжпредметних зв'язків у шкільному навчанні очевидна.
Одним із варіантів вирішення проблеми міжпредметних зав’язків є інтегрування навчального матеріалу.
Він обумовлений сучасним рівнем розвитку науки, на якому яскраво виражена інтеграція суспільних, природничих і технічних знань. Інтеграція наукових знань, у свою чергу, пред'являє нові вимоги до фахівців. Зростає роль знань людини в області суміжній зі спеціальністю наук і умінь комплексно застосовувати їх при вирішенні різних завдань. Здійснення міжпредметних зв'язків на практиці викликає чимало труднощів: як організувати пізнавальну діяльність учнів, щоб вони хотіли і вміли встановлювати зв'язки між різними навчальними предметами як викликати їх пізнавальний інтерес до світоглядних питань науки; яким чином об'єднати зусилля вчителів різних предметів у досягненні виховного ефекту навчання? Зміст, обсяг, час і способи використання знань з інших предметів можна визначити тільки на основі планування. Новий зміст фізико-математичної освіти в середніх загальноосвітніх навчальних закладах наблизив розглядувані навчальні дисципліни до рівня сучасного наукового знання. Глибокі зв’язки, які існують між математикою та іншими науками, мають знайти адекватне відображення у зв’язках між відповідними дисциплінами. Сьогодні ні в кого не викликає сумнівів той факт, що лише при оптимальному функціонуванні міжпредметних зв’язків можливе реальне підвищення якості знань школярів.
Математика в школі - це база для проведення інтегрованих уроків, так як зміст будь-якого іншого шкільного предмета може розглядатися в якості інформації того чи іншого виду. Інтегрований урок, побудований на базі математики, дозволяє конкретизувати знання, вміння та навички і застосувати їх на практиці, допомагає розвитку математичного мислення школярів і дає можливість вчителю продемонструвати найбільш важливі прийоми і методи розумової діяльності в нестандартних ситуаціях.
Реалізація інтегрованих уроків досягається в процесі інтеграції уроків математики з іншими предметами. Тематичний підхід об'єднує в одне ціле завдання з різних областей. Працюючи над темою, школярі користуються знаннями, отриманими на уроках математики, використовуючи при цьому здобуті знання на уроках природничого циклу: фізики, хімії, економіки, та предметів суспільно-гуманітарного циклу: історії, трудового навчання, образотворчого мистецтва тощо. Крім того, інтеграція допомагає дитині зв'язати те нове, про що вона дізнається, з чимось знайомим і зрозумілим з реального життя.
Головна мета інтеграції - створення у школяра цілісного уявлення про навколишній світ, тобто формування світогляду. Розглянемо деякі можливості при інтегрованому побудові навчального процесу, що дозволяють якісно вирішувати завдання навчання і виховання учнів:
1. Перехід від внутріпредметних зв'язків до міжпредметних дозволяє учневі переносити способи дій з одних об'єктів на інші, що полегшує навчання і формує уявлення про цілісність світу. При цьому слід пам'ятати, що такий перехід можливий лише за наявності певної бази знання внутріпредметних зв'язків, інакше перенесення може бути поверховим і механічним.
2. Збільшення частки проблемних ситуацій у структурі інтеграції предметів активізує розумову діяльність школяра, змушує шукати нові способи пізнання навчального матеріалу, формує дослідний тип особистості.
3. Інтеграція веде до збільшення частки узагальнюючих знань, що дозволяють школяреві одночасно простежити весь процес виконання дій від мети до результату, осмислено сприймати кожен етап роботи.
4. Інтеграція збільшує інформативну ємність уроку.
5. Інтеграція є засобом мотивації навчання школярів, допомагає активізувати навчально-пізнавальну діяльність учнів, сприяє зняттю перенапруги та втоми.
6. Інтеграція навчального матеріалу сприяє розвитку творчого мислення учнів, дозволяє їм застосовувати отримані знання у реальних умовах, є одним з істотних чинників виховання культури, важливим засобом формування особистісних якостей, спрямованих на добре ставлення до природи, до людей, до життя.
2.3 Застосування компетентісних задач
Сформованість в учнів ключових, освітніх і предметних компетенцій перевіряються поступово на протязі всього періоду навчання, але особливе місце займає в перевірці сформованості компетенцій Державна Підсумкова Атестація (ДПА) і Зовнішнє Незалежне Оцінювання (ЗНО).
Тому в роботі кожного вчителя особливе місце займає підготовка учнів до ДПА і ЗНО, а саме – формування предметних компетенцій.
Але підготовка до ДПА і ЗНО проходить не тільки в 9 або 11 класі, але протягом всього навчання. Тому підготовка до цих випробувань починається з першого уроку навчального курсу з будь-якої дісципліни.
Такий підхід дозволяє здійснювати постійний контроль за роботою учнів та самоконтроль вчителя щодо забезпечення необхідних умов опанування учнями навчальним матеріалом, вибору оптимальних методів навчання, удосконалення практичної завантаженості уроків. На основі державних вимог до знань та вмінь скадаються різнорівневі завдання, завдання з вибором однієї або кількох вірних відповідей, встановлення послідовності або відповідності. Учням пропонується робота з порівняльними таблицями, з блок-схемами та діаграмами, завданнями для розвитку системного і аналітичного мислення як основи формування базових і предметних компетенцій.
Суттєво ускладнюється робота вчителя в 9-11 класах, коли підготовка до ДПА і ЗНО стає актуальною і в багатьох випадках зумовлює навчальні інтереси і потреби учнів.
По перше – потрібно організувати повторення навчальних тем і розділів безпосередньо на уроках. Для правильної організації повторення не тільки на репродуктивному але і на творчому рівні з врахуванням інтелектуального росту учнів необхідно зробити декілька кроків:
1. Ретельно вивчити документацію щодо ДПА і ЗНО, звернути увагу на розподіл питань втестових завданнях, на предметні компетенції, сформованість яких перевіряється ЗНО і
ДПА.
2. Скласти орієнтовний перелік тем для повторення і за можливостями інтегруватиматеріал повторення з новим матеріалом
3. Подавати завдання на повторення в формі, яка буде запропонована учням на ДПА і ЗНОПоряд з повторенням в 9-11 класах продовжується вивчення нового матеріалу, формуються нові предметні компетенції.
Але організація навчання в 9 класі і в старшій школі вимагає від вчителя урахування вікової психології і прагнення юнаків до самовдосконалення, вже сформовані навички самоконтролю і вміння планувати і коригувати власні дії. Ефективно організувати навчальний процес дозволяють державні вимоги до предметних компетенцій.
На початку вивчення розділу або теми доцільно ознайомити учнів з держвимогами щодо предметних комптенцій ( за чинною програмою) і встановити для себе три рівні сформованості
1) не знаю, не вмію
2) частково знаю, володію, потребую допомоги
3) знаю, вмію, можу надати допомогу
Протягом терміну вивчення теми варто запропонувати учням здійснювати «ревізію» сформованості комптенцій. Ця робота дозволить учням спостерігати за власним зростанням ( + мотивація), виявляти недоробки, своєчасно коригувати знання, посилити самосійну роботу.
Особливе значення має аналіз сформованості предметних компетенцій наприкінці вивчення теми під час підготовки до узагальнення або контролю. Проведений учнями аналіз дозволить встановити «білі плями» в знаннях та вміннях і на узагальнюючому уроці їх ліквідувати. Варто запропонувати завдання ЗНО минулих років прикладного характеру (Додаток 3).
Систематична робота учнів з вимогами до знань та вмінь дозволяє учням свідомо підходити до навчання і опанування певним навчальнім матеріалом, робити свідомий вибір форм навчання, а також здійснювати самоконтроль і своєчасно коригувати власні помилки.
Систематична комплексна робота над вивченням нових тем і повторення з урахуванням держвимог до предметних комптенцій учнів, створення спільно з учнями програм підготовки дозволять кожному учню належним чином підготуватися до вирішальних випробувань у своєму житті.
ВИСНОВКИ
В ході написання навчально-методичного посібника проведено дослідження проблем формування інтегративно-компетентісного підходу до викладання математики в основній та старшій школі. В даному посібнику розкрито поняття математичної компетенності, як основної складової життєвої компетентності, визначено основні методи навчання математики, що формують математичну компетентність та розкрито суть інтеграції навчального матеріалу як в межах одного предмету так і поєднання навчального матеріалу з математики з матеріалом інших дисциплін, що дозволить найкраще опанувати зміст тих чи інших тем. Крім цього, в навчально-методичному посібнику визначені шляхи удосконалення процесу навчання математики в загальноосвітніх навчальних закладах і підвищення ефективності використання міжпредметних зав’язків в навчально – виховному процесі, окреслено напрямки і шляхи інтеграції навчальних предметів з курсом математики з метою розвитку пізнавальної активності та формування основних життєвих компетенцій .
Результати дослідження дають підставу сформулювати такі висновки:
1) Інтеграціно-компетентісний підхід до викладання математики забезпечуєтьсясистематичним використанням інтегрованих завдань, що сприяють: а) розвитку абстрактного та образного мислення; б) формуванню навичок математичного моделювання та дослідженню на їх основі реальних процесів і явищ; в) кваліфікованому оволодінню інформаційними технологіями.
2) Серед методів навчання,що сприяють формуванню математичної компетентностіпереважають продуктивні, розвиваючі методи дослідницького характеру
3).Ефективнiсть використання інтегрованих завдань для організації засвоєння нових знань безпосередньо пов'язана з самостiйним одержанням знань, використанням внутрiшньопредметних зв'язкiв, а також із осмисленням i закрiпленням нових знань.
4) Результативність використання інтегрованих завдань також залежить вiд рівня їх адаптації до рiзних типiв урокiв, складностi матерiалу, підготовленості учнiв до навчання.
5) Використання системи інтегрованих завдань при вивченні основ інформатикидозволяє суттєво поглибити зміст міжпредметних зв`язків на основі ідеї інтеграції знань, посилити мотивацію навчання, активізувати весь навчальний процес, надати йому творчого, дослідницького спрямування.
Інтеграційно-компетентісний підхід сприяє свідомому розумінню спроможності учнів бачити та застосовувати математику в реальному житті, розуміти зміст і метод математичного моделювання, будувати математичну модель, досліджувати її методами математики, інтерпретувати отримані результати, оцінювати похибку обчислень. вибору учнями форм навчання.
СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ
1. Бібік Г.В. Компетентнісний підхід у навчанні математиці як методична проблема: наукові записки / Г.В. Бібік // — Ч.1.— Кіровоград: РВВ КДПУ імені В.Винниченка, 2009.— Випуск 82. –– С. 11–15. — (Серія «Педагогічні науки»).
2. Бібік Г.В. Використання задач з міжпредметним змістом як засіб формування математичної компетентності випускника. / Г.В. Бібік // Науковий часопис Національного педагогічного університету імені М.П.Драгоманова. / За ред. П.В. Дмитренка, В.Д. Сиротюка. [зб. наук. праць] № 5. — К.: Видавництво НПУ імені
М.П. Драгоманова, 2016. — Випуск 19. — С.31 – 39. — (Серія «Педагогічні науки: реалії та перспективи»).
3. 1. Бевз В. Г. Використання історизму у шкільному курсі математики: Практикум з історії математики: Навчальний посібник. ⎯ К.: НПУ імені М. П. Драгоманова, 2009.
4. Бевз Г. П. Методи навчання математики. ⎯ Х.: Основа, 2013.
5. Думіна И.В. Педагогические технологии в обучении географии. - М.: Школа-Пресс, 2001. - 158с.
6. Єфімова О., Шафрін Ю. Практикум по компьютерной технологии. - М.: МЦМНО, 2016 - 325с.
7. Зеленяк О.П. Інтегровані уроки з математики та інформатики в класах з поглибленим вивченням цих предметів // Комп’ютер в школі та сім’ї. - 2006. - №4. -С.16.
8. Кирдей І.Д. Моніторингові дослідження альтернативних методів проведення уроків узагальнення та систематизації // Комп’ютер в школі та сім’ї. -2003. - №7. - С.22.
9. Крючкова Т.М., Кармазіна В.В., Гранкіна Т.О. Система контролю знань за допомогою сучасних інформаційних технологій // Комп’ютер в школі та сім’ї. -2006. - №4. - С.32.
10. Мерзляк А. Г., Полонський В. Б., Якір М. С. Алгебра. 8 клас. ⎯ Х.: Гімназія, 2016.
11. Раков С.А. Пакет DG та дослідницький підхід у курсі алгебри та початків аналізу // Комп’ютер в школі та сім’ї. - 2005. - №4. - С.29.
12. Овчарук О. Л. Компетентності як ключ до оновлення змісту освіти в Україні. Стратегія реформування освіти в Україні.Щербань Т. Модель компетентного випускника: г.
«Завуч». – 2005.№28.
13. Якіманская И.С. Личностно-ориентированное обучение в современной школе. - М.:
Школа-Пресс, 1996. - 165с.
Додаток 1
Задачі прикладного змісту в курсі викладання геометрії
Подібні фігури
1. Тінь, що відкидається стовпом на поверхню землі, дорівнює 9 м, у той самий час стрижень висотою 2 м відкидає тінь 2,4 м. Знайти висоту стовпа.
(Відповідь: 7,5 м) 2. Стовп висотою 15 м закривається монетою діаметром 2 см, якщо тримати її на відстані 70 см від ока. Знайти відстань від стовпа до спостерігача.
(Відповідь: 525 м)
3. Як знайти висоту предмета, до основи якого можна підійти?
4. Як знайти висоту предмета, до основи якого не можна підійти?
Теореми синусів і косинусів
1. О 7 годині ранку пасажирський літак вилетів з міста А. Після півгодинної зупинки в місті В о 8 год 10 хв літак зробив поворот на 35° вправо та о 9 год здійснив посадку в місті С. Знайти відстань між містами А та С, якщо середня швидкість літака на кожній ділянці польоту дорівнювала 320 км/год.
(Відповідь: 
458 км) 2. З двох пунктів А та В виїжджають одночасно два потяги відповідно у напрямах AD і BE, що перетинаються в точці С під кутом 60°. Обидва потяги рухаються рівномірно зі швидкістю відповідно 20 і 30 км/год. Через скільки годин з моменту їхнього відправлення відстань DE між ними дорівнюватиме початковій, якщо АС = 50 км, ВР = = 40км?
(Відповідь: 3 год) 3. Зі спостережного пункту помічають під кутом 63,5° літак, що пролітає над вежею, висота якої 79,5 м. Пряма, що сполучає спостережний пункт із верхівкою вежі, утворює з горизонтальною площиною кут 20°45'. На якій висоті знаходиться літак?
(420,5 м) 4. З вертольота, що знаходиться над шосейною дорогою, було помічено колону машин, яка рухається по ній. Початок колони видно під кутом 75° , а кінець - під кутом 70°. Знайти довжину колони, якщо вертоліт знаходиться на висоті 1650 м.
( 1042 м)
5. Вершину гори з точки А видно під кутом 38° 42', а при наближенні до гори на 200 м вершину стало видно під кутом 42°. Знайти висоту гори.
( 14 325 м) 6. Дорога вгору піднімається двома уступами у вигляді ламаної лінії. Перший уступ утворює з горизонтом кут 30°, другий - 65° , а пряма, що сполучає вершину гори з її основою, нахилена до горизонту під кутом 60° .Довжина першого уступу дорівнює 1 км.
Знайти висоту гори.
( 5,7 км) 7. На горі стоїть вежа висотою 100 м. Біля підніжжя гори знаходиться одна людина. Інша спостерігає її спочатку з вершини вежі під кутом 60? до горизонту, а потім з її основи під кутом 30°. Знайти висоту гори.
(50 м)
Ламана. Многокутник. Правильні многокутники
1. Села А та В знаходяться на однаковій відстані від міста М. На прямій, що проходить через М і В, розміщені ще два села С та D. До яких із сіл (А чи В) ближче розміщено село С; село D?
(С ближче до B,D ближче до А) 2. Чотири будинки розміщені у вершинах земельної ділянки, що має форму опуклого чотирикутника. Де на цій ділянці потрібно викопати колодязь, щоб сума всіх відстаней від кожного будинку до колодязя була найменшою?
(У точці перетину діагоналей чотирикутника) 3. Кути квадратного залізного листа зі стороною а зрізали так, що отримали правильний восьмикутник. Знайти його сторону.
( 0,41а) 4. На колі потрібно розмістити центри отворів для 15 болтів так^ щоб відстань між центрами отворів була ЗО мм. Якоїдовжини має бути радіус кола?
(72 мм) 5. Як скласти паркет із правильних восьмикутників і квадратів; із дванадцятикутників і трикутників?
6. Чи можна скласти паркет із правильних десятикутників і п'ятикутників?
(Ні) 7. З яких правильних многокутників одного виду можна скласти паркет?
(Трикутників, квадратів, шестикутників)
Вписані та описані многокутники
1. Де на відкритій ділянці трикутної форми потрібно помістити ліхтар, щоб усі три кути її були освітлені однаково?
(У центрі кола, описаного навколо трикутника) 2. З колоди діаметром 120 мм необхідно випиляти брус товщиною 40 мм. Знайти найбільшу ширину бруса.
(113мм) 3. Скляреві доручили вирізати скло для вікна круглої форми. Що і як має скляр виміряти, користуючись лише рулеткою, щоб вирізати потрібне скло?
(Треба взяти три точки на краях вікна та виміряти відстані між ними. Побудований за трьома сторонами трикутник однозначно задає описане коло)
4. З колоди потрібно випиляти 7 дощок однакової ширини товщиною 40 мм кожна. Знайтинайбільшу ширину кожної дошки, якщо діаметр колоди 350 мм.
(210 мм)
5. З кількох колод однакового діаметра випилюють балки різного поперечного перерізу.
Для якого перерізу балки відходів буде найменша кількість?
(Якщо балка матиме квадратний переріз)
Довжина кола
1. Ведуче колесо паровоза робить 6 об/с, діаметр колеса 120 см. Знайти швидкість паровоза.
( 81 км/год) 2. Піднімаючи воду з колодязя, вал робить 18 оборотів. Обчислити глибину колодязя, якщо діаметр вала 20 см.
(11,3м)
3. Довжина хвилинної стрілки на Спаській вежі Московського Кремля 3 м 27 см. Якийшлях пробігає її кінець за 1 хв? за 1 годину?
(33,56 см; 2053,56 см)
4. Внутрішня сторона бігової доріжки стадіону має форму, зображену на малюнку.
Довжина кожної з прямолінійних частин доріжки дорівнює 100 м. Довжина всієї доріжки дорівнює 400 м. Обчислити ширину стадіону.
(63,6 м)
5. З жерсті зробили одну трубу діаметром 18 см і три однакові труби тієї самої довжини.
Обчислити радіус менших труб.
(3 см). 7. Діаметри коліс трактора дорівнюють 75 і 90 см. Який шлях пройде трактор, якщо на цьому шляху переднє колесо зробить на 230 обертів більше, ніж заднє?
( 3,3 км) 8. Довжина орбіти автоматичної космічної станції «Салют» дорівнює 41 500 км. Вважаючи орбіту круговою, знайти висоту станції над Землею, якщо радіус Землі 6370 км.
( 238 км) 9. Тунель циліндричної форми, що має діаметр 135 см і глибину 380 м, треба викласти цеглою. Скільки цеглин для цього буде потрібно, якщо розмір цегли 25 см х 12 см х 6,5 см?
(826 цеглин)
10. Припустимо, що земну кулю та футбольний м'яч обтягнуто по екватору обручами.Якщо в обох випадках збільшити довжину обручів на 1 м і розмістити знову обручі на однаковій відстані від поверхні об'єктів, то утворяться зазори. У якому випадку зазор більший?
(Однаковий завжди)
11. За два обороти по круговій орбіті навколо Землі космічний корабель пролетів 84152 км.На якій висоті над поверхнею Землі знаходиться корабель, якщо радіус Землі дорівнює 6370 км?
(330 км) 12. Знайти довжину маятника стінного годинника, якщо кут його коливання становить 38°, а довжина дуги, що описує кінець маятника, дорівнює 24 см.
( 36,2 см) 13. Тепловоз пройшов 1413 м. Знайти діаметр колеса, якщо воно зробило 300 обертів.
(1,5м) 14. Радіус заокруглення шляху залізничного полотна дорівнює 5 км, а довжина дуги заокруглення — 400 м. Яка градусна міра дуги заокруглення?
( 4°35')
Кутова міра дуги кола
1. Скільки спиць у колесі, якщо кожний з кутів, розміщених між двома сусідніми спицями, дорівнює 18°?
(20) 2. Зубчасте колесо з 60 зубцями зчеплене з іншим, що має 75 зубців. На який кут повернеться друге колесо при одному повному оберті першого?
(288°)
3. Діаметри двох зчеплених зубчастих коліс відносяться як 3 : 8. На який кут повернеться більше колесо при одному повороті меншого?
(135°) 4. На який кут повернеться Земля навколо своєї осі за 8 год? На який кут за цей час повернеться годинна стрілка?
(120°;240°) 5. Як змінюється кут між годинною і хвилинною стрілками впродовж 1 хв; 12 хв; 46 хв?
(5°30'; 66°; 253°)
Площі многокутників
1. Основа постаменту пам'ятника має форму квадрата зі стороною 6 м. Навколо пам'ятника розміщена клумба шириною 2 м. Знайти площу клумби.
(64м2) 2. Освітлення кімнати вважається нормальним, якщо площа прорізів вікон не менша за 0,2 площі підлоги. Визначити, чи нормально освітлена ваша класна кімната.
3. Необхідно оштукатурити стіну довжиною 8,25 м і висотою 4,32 м, що має три вікна розміром 2,2 м х 1,2 м кожне. Знайти площу поверхні стіни, яку необхідно оштукатурити.
(27,72 м2) 4. Сад має форму прямокутника зі сторонами 580 м і 376 м. Скільки в ньому яблунь, якщо на кожну яблуню припадає в середньому 16м2? Який виторг дав сад після продажу яблук, якщо з 1 га зібрано по 35 т яблук і кожна тонна продана в середньому по 2,5 грн?
(13 630 яблунь, 1907,5 грн) 5. Підлогу кімнати, що має прямокутну форму розміром 11 м х 8,8 м, потрібно вистелити паркетом, одна плитка якого має розмір 5 см х х 25 см. Скільки потрібно плиток паркету, якщо на припасування і прирізку витрачається 3 % від загальної площі? t
(7977 плиток) 6. Кожну із двох рівновеликих ділянок потрібно обнести огорожею. Одна ділянка має форму квадрата зі стороною 80 м, а інша — форму прямокутника, одна сторона якого дорівнює 50 м. На яку огорожу буде потрібно більше матеріалу і на скільки, якщо на кожні 12 м потрібно 1 м3 пиломатеріалів?
(Прямокутної форми; на 3 м3) 7. Трактор, рухаючись зі швидкістю 15 км/год, тягне за собою дискову сівалку з робочою шириною захвату 6 м. Скільки гектарів можна засіяти у такий спосіб за 8-годинний робочий день?
(72га)
8. До будинку необхідно зробити добудову з трьох стін, використовуючи одну зі стін будинку. Виявилося, що цегли вистачить на 100 м стіни (по периметру трьох нових стін).
Добудова має бути максимальною за площею. Які розміри добудови вибрати?
(25м х 50 м) 9. Прямокутна квіткова клумба займає площу 216 м2 .Уздовж довгих сторін необхідно прокласти доріжки шириною 2 м, уздовж коротких — шириною 3 м. Які мають бути розміри прямокутної ділянки (клумби разом з доріжкою), щоб площа доріжок була найменшою?
(24 м х 16 м) 10. Один новосел вирішив вистелити різнобарвними квадратними плитками підлогу в кухні площею 7,29 м2 і купив такий набір: 1 плитка зі стороною 120 см, 3 плитки зі стороною 90 см, 9 плиток із стороною 60 см і 2 плитки зі стороною 30 см. Інший новосел для такої самої підлоги купив 2 плитки зі стороною 120 см, 2 плитки зі стороною 90 см, 8 плиток зі стороною 60 см і 2 плитки зі стороною 30 см. Хто з них вигадав?
(Перший) 11. Ділянку, що має форму прямокутника, потрібно розділити двома межами, що виходять з одного кута, на три рівновеликі частини. Як це зробити?
(Сполучити вершину кута з точками на протилежних сторонах, які ділять сторони у відношенні 1: 2)
12. Ділянку, що має форму прямокутника, потрібно розділиш трьома межами на чотирирівновеликі частини. Як це зробити?
(Сполучити вершину прямокутника з протилежною їй вершиною і серединами сторін)
13. Поверхня озера має форму квадрата. У вершинах квадрата на березі озера ростутьчотири дуби. Треба удвічі збільшити площу поверхні озера так, щоб нове озеро зберегло форму квадрата і щоб усі чотири дуби залишилися на своїх місцях. Як це зробити?
14. Потрібно вистелити підлогу кімнати розміром 6 м х 4 м плитками правильноїшестикутної форми. Скільки таких плиток необхідно мати, якщо сторона плитки 20 см?
( 243 плитки) 15. Підлогу прямокутного фойє театру, розміри якого 4,6 м х 8,4 м, потрібно покрити керамічною плиткою двох різних кольорів (порівну кожного кольору). Скільки потрібно плиток кожного кольору, якщо плитка має форму правильного шестикутника зі стороною 10 см?
(2359 плиток кожного кольору) 16. На плані, виконаному в масштабі 1:200, місце для установки деякого об'єкта займає 360 см2. Яку площу воно займає насправді?
(1440см2)
Площа круга та його частин
1. Дерево має 1,884 м в обхваті. Чому дорівнює площа поперечного спилу, що має приблизно форму кола?
( 0,28 м2) 2. Вода тече по двох трубах із однаковою швидкістю. Перша труба має діаметр 20 см, а друга — 15 см. У скільки разів подача води з другої труби менша ніж з першої?
(приблизно в 1,8 раза) 3. Круглу клумбу, радіус якої 6 м, розділили на дві рівні частини колом, центр якого збігається з центром клумби. Чому дорівнює радіус цього кола?
4. Дві труби, внутрішні діаметри яких дорівнюють 15 мм і 25 мм, потрібно замінитиоднією, не змінюючи їхньої пропускної здатності. Яким має бути внутрішній діаметр нової труби?
( 29мм)
5. Два прожектори розміщені один напроти іншого на прямолінійних паралельнихпротилежних берегах ріки. Відстань між прожекторами дорівнює 12 км. Прожектори можуть освітлювати місцевість радіусом 10 км кожний. Чому дорівнює площа поверхні ріки, освітлюваної цими прожекторами?
Додаток 2
Редактор
_______________________
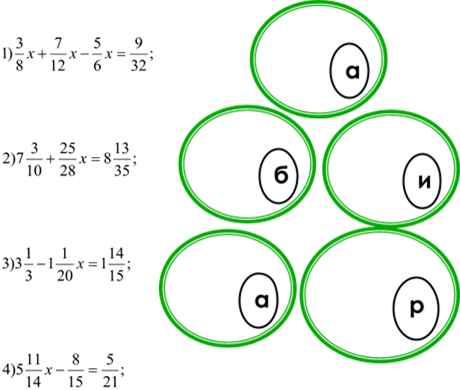
2.Додавання дробів з різними знаменниками.
3.Множення звичайних дробів. Ділення звичайних дробів.
§ 1. Основна
властивість дробів. Скорочення дробів.
1.Кожен звичайний дріб – це результат від ділення чисельника на
_________.
|
28 =28____123. |
|
123
2.Якщо _________ і _________дробу помножити або___________ на одне і те саме число,відмінне від__, то отримаємо ___________рівний ________.Це __________ властивість дробу.
|
|
|
|
|
3.Під час скорочення дробу |
необхідно |
чисельник і знаменник |
|
дробу_________ на найбільший знаменника. |
спільний |
____________чисельника і |
|
Наприклад, |
|
|
3 6 .
3.Якщо чисельник і знаменник дробу – числа взаємно_______, то такий дріб називають нескоротним.
§ 2. Додавання і віднімання звичайних дробів.
|
|
1.Сума дробів з однаковими знаменниками дорівнює дробу, в якому ____________той самий, а чисельник дорівнює сумі ______________даних дробів.
5 5 5 .
2.Різниця дробів з однаковими знаменниками дорівнює дробу, в якому знаменник____________,а чисельник дорівнює___________чисельників даних дробів.
|
Наприклад, |
5 5 5 .
3.Щоб знайти суму чи різницю дробів з різними знаменниками, необхідно спочатку звести їх до спільного___________, а потім________або________по відомим правилам додавання дробів з однаковими знаменниками.
§ 3. Множення і ділення звичайних дробів.
|
Наприклад, |
1.Добуток двох дробів дорівнює дробу, чисельник якого є __________чисельників даних дробів, а _____________– добутком їх знаменників.
.
2.Числа, добуток яких дорівнює 1, називаються взаємно_________.
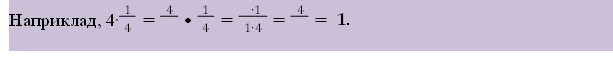
3.Щоб ________дріб на дріб, необхідно ділене помножити на дріб, обернений _________.
Наприклад, 
.
Між прикладами та відповідями встановити відповідність.
а) 34 • 89 ; б) 45 : 2516 ; в) 3 43 ∙5 25 ; г) .
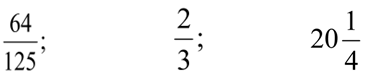
а) 36 ; 1418 ; б) 155 ; 46 ;
Леонардо Фібоначі
1202 рік придумав запис дробів.
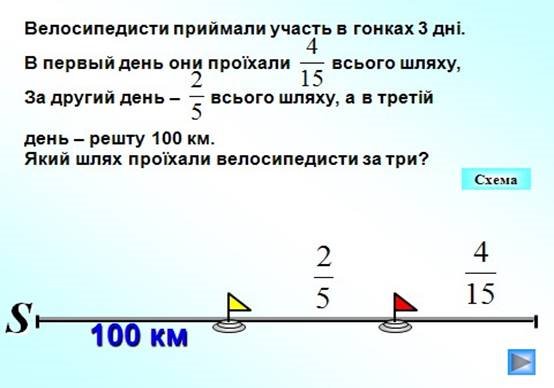
Задача№1
Задача№2
Додаток 3
Завдання прикладного змісту в ЗНО
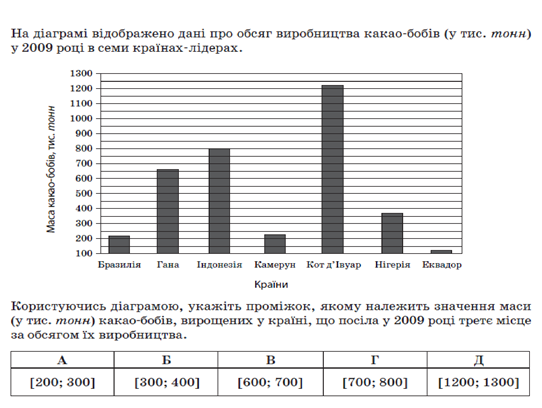
Завдання ЗНО 2016-2017
1.
2.
● 
● 3.
● 
4.
5.
6.
7.
про публікацію авторської розробки
Додати розробку