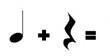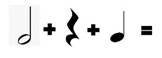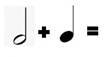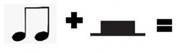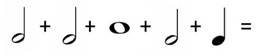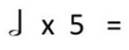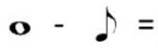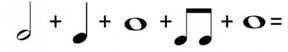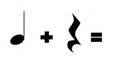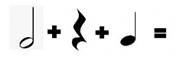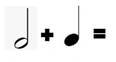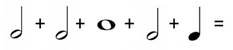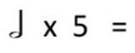Інтегративні зв'язки математики та з іншими навчальними предметами

Про матеріал

У документі "Інтегративні зв'язки математики та з іншими навчальними предметами" можна знайти цікаві задачі, які демонструють зв'язок математики з іншими предметами. 1. Зв'язки математики і статистики. 2. Зв'язки математики та біологія. 3. Зв'язки математики та географія. 4. Зв'язки математики і фізика. 5. Зв'язки математики і хімії. 6. Зв'язки математики та економіки. 7. Зв'язки математики та інформатики. 8. Зв'язки математики та музики.

Перегляд файлу

Інтегративні зв’язки математики з іншими навчальними предметами

Математика та статистика

Задача 1. Випускники Кропивницького вище професійного училища працюють у трьох різних компаніях: 17 осіб – у банку, 23 – у фірмі та 19 – у податковій інспекції. Знайдіть ймовірність того, що випадково зустрінутий випускник працює у фірмі.

Розв’язання

За умовою задачі ми повинні знайти ймовірність того, що випадково зустрінутий випускник працює у фірмі.

Кількість (осіб)	Компанія	Всього
17	Банк	59
23	Фірма
19	Податкова інспекція

Всього: 17 + 23 + 19 = 59 (осіб) – випускників працює Формула ймовірності: 𝑃(𝐴) = ^𝑚

𝑛

𝑚 − кількість сприятливих подій,𝑛 − загальна кількість подій

За умовою ми знаємо, що у фірмі працює 23 осіб.

Тоді ймовірність того, що випадково зустрінутий випускник працює у фірмі 𝑃(𝐴) = = 0,3893

Задача 2. В училищі опитали деяких хлопців і дівчат з паралелі 1-х курсів про час, який вони витрачають на допомогу батькам по домашньому господарству. Виявилося, що учні та учениці КБ-21 в середньому витрачають 1,1 год на добу, а учні та учениці ТБ-21 – 1,7 год на добу.

1) Користуючись цими даними, оцініть середній час, який витрачає учень училища на допомогу батькам на добу.

2) Як потрібно змінити відповідь, якщо додатково відомо, що в училищі навчаються 400 дівчат і 560 хлопців?

Розв’язання

1) Визначимо середнє значення, тобто скільки годин в середньому витрачають учні на допомогу батькам.

1,1 + 1,7 2,8

= = 1,4 (год)

2 2

2) За умовою нам відомо, що в училищі навчаються 400 дівчат і 560 хлопців.

Тоді, нам потрібно знайти ймовірність. Припустимо, що 560 хлопців витрачають 1,1 год, а дівчата – 1,7 год.

Примітка: правило суми – якщо деякий об’єкт А можна вибрати m способами, а другий об’єкт B можна вибрати n способами, то вибір «або A, або B» можна здійснити m+n способами.

Задача 3. За даними Державної служби статистики України (станом на 2021 рік), найбільш популярними професіями в Україні є:

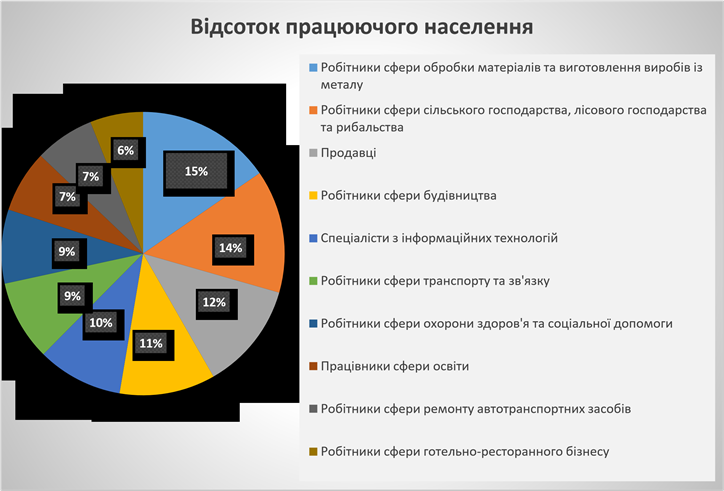
Знайдіть:

1) Розмах, моду й середнє значення з даної статистики.

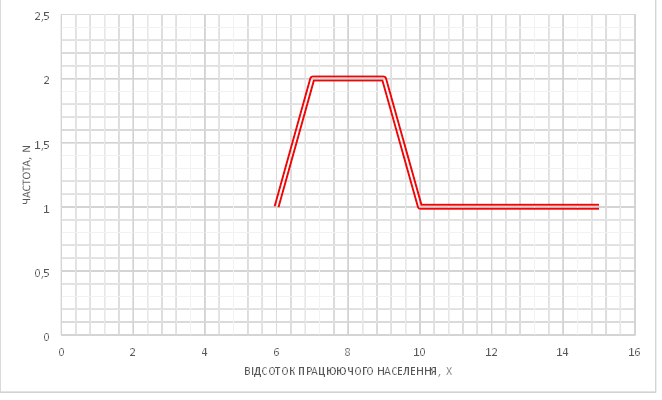
2) Побудуйте полігон частот значень відсотків працюючого населення.

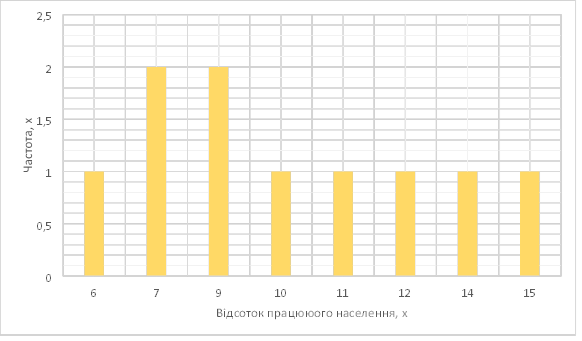
3) Побудуйте гістограму частот.

4) Напишіть, які фактори можуть змінити такий відсоток?

Розв’язання

1) Розмах: 𝑅 = 15% − 6% = 9%

Мода: Мо = 7%, Мо = 9%

15%+14%+12%+11%+10%+9%+9%+7%+7%+6% 100%

Середнє значення: = =

10 10

10%

2) Складемо таблицю частот:

Відсоток працюючого населення, x	15	14	12	11	10	9	7	6
Частота, n	1	1	1	1	1	2	2	1

Полігон:

Гістограма:

4) Дані про популярні професії в Україні можуть змінюватись під впливом різних факторів, зокрема:

1. Економічна ситуація в країні - рівень безробіття, стан галузей економіки, інвестиційна привабливість тощо можуть впливати на популярність окремих професій.

2. Розвиток нових технологій - з'явлення нових галузей та професій, зміна вимог до кваліфікації та навичок працівників, можуть змінювати популярність окремих професій.

3. Соціальні та демографічні тенденції - зміни в національному складі населення, збільшення частки жінок на ринку праці, зміни вікової структури населення тощо також можуть впливати на популярність окремих професій.

4. Рівень оплати праці та умови праці - висока зарплата, гнучкий графік роботи, можливість працювати з вдома тощо можуть зробити певну професію більш привабливою для працівників.

5. Система освіти та підготовки кадрів - якість освіти, наявність професійної підготовки та можливості для отримання додаткових кваліфікацій можуть впливати на рівень кваліфікації працівників та їхню привабливість для роботодавців.

6. Політична ситуація в країні та за її межами - війна, конфлікти, еміграція можуть впливати на популярність окремих професій та змінювати зону інтересів працівників.

7. Культурні та соціальні стереотипи - деякі професії можуть бути вважатись більш престижними або менш привабливими залежно від культурних та соціальних уявлень.

8. Конкуренція на ринку праці - наявність великої кількості кваліфікованих працівників на ринку праці може знизити популярність певних професій, а також впливати на рівень оплати праці.

9. Розвиток ринку та бізнесу - зміни в галузевій структурі, поява нових підприємств та інновацій можуть впливати на популярність окремих професій та створювати нові можливості для працівників.

10. Екологічна ситуація - стан навколишнього середовища, екологічні проблеми та ризики можуть впливати на розвиток окремих галузей економіки та змінювати популярність певних професій.

Примітка:

Різниця найбільшого і найменшого значень випадкової величини вибірки називається її розмахом і позначається R.

Мода (позначають Mo) — це значення випадкової величини, що має найбільшу частоту в розглянутій вибірці.

Математика та біологія

Задача 1. Нехай популяція в момент часу 𝑡 с налічує 𝑝(𝑡) осіб 𝑝(𝑡) = 3000 + 100𝑡². Знайдіть швидкість зростання популяції:

1) в довільний момент 𝑡

2) в момент 𝑡 = 1 с

Розв’язання

1) За допомогою похідної знайдемо швидкість зростання популяції в довільний момент 𝑡

𝑣 = 𝑝^′(𝑡) = (3000 + 100𝑡²)^′ = 2 ∙ 100𝑡 = 200𝑡

2) Знайдемо в момент 𝑡 = 1 с

𝑝^′(𝑡) = 𝑝^′(1) = 200𝑡 = 200 ∙ 1 = 200

Задача 2. Кількість популяції польових мишей розвивається за законом 𝑓^′(𝑡) = 0,07 ∙ 𝑓(𝑡), де 𝑓(𝑡) – кількість мишей в момент часу 𝑡 (місяців).

1) За який час популяції зросте зі 170 польових мишей до 3000?

2) З якою швидкістю розмножуються миші?

Розв’язання

1) Функція 𝑓 має вигляд: 𝑓 𝑒^𝑘𝑡. Із умови випливає, що 𝑘 = 0,07.

При 𝑡 . Отже, 𝑓^𝑡.

Тоді ^𝑡. Звідси 𝑡 місяців

𝑒 ⇒ 𝑒 ⇒ 𝑡

𝑡 місяців

б) Миші розмножуються зі швидкістю 𝑣^𝑡 в місяць.

Математика та географія

Задача 1. Відрізку на карті, довжина якого 4,7 см відповідає відстань на місцевості в 94 км. Яка відстань між містами Кропивницьким і Балта (Одеська область), якщо на карті її зображено відрізком 12,6 см?

Розв’язання

Переведемо км в см: км см

1) (р.) – у скільки разів зменшиться відстань на

карті

2) – відстань

між містами

Відповідь: 252 км відстань між містами, якщо на карті її зображено відрізком 12,6 см.

Задача 2. Найбільший острів у світі – це Гренландія. Площа поверхні дорівнює 2 166 086 квадратних кілометрів. Гренландія – це окрема держава та її населення за даними ООН у 2023 році становить 57 047 чоловік. Скільки людей припадає на 1 квадратний кілометр острова?

Розв’язання

Щоб визначити скільки людей припадає на 1 квадратний кілометр острова потрібно площу поверхні поділити на населення.

Відповідь: 0,03 чол./км² людей припадає на 1 квадратний кілометр

острова.

Математика і фізика

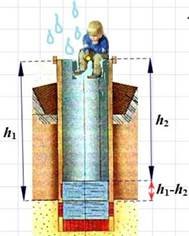Задача 1. Після дощу рівень води в колодязі може збільшитися. Хлопчик вимірює час t падіння невеликих камінчиків у колодязь і розраховує відстань до води за формулою ℎ = 5𝑡², де h - відстань в метрах, t - час падіння в секундах. До дощу час падіння камінців становив 0,6 с. На скільки має піднятися рівень води після дощу, щоб час, що вимірюється, змінився на 0,2 с? Відповідь висловіть у метрах.

Розв’язання

Знайдемо рівень води до дощу. За умовою, ми вже

знаємо формулу, яка розраховує відстань до води: ℎ = 5𝑡².

ℎ₁ = 5𝑡² = 5 ∙ (0,6)² = 5 ∙ 0,36 = 1,8 (м) – відстань/рівень води до дощу

Знайдемо тепер рівень води після дощу. Ми знаємо, що до дощу час падіння камінців становить 0,6 с. і за умовою ми також знаємо, що рівень води після дощу повинен змінитися. Але час змінився на 0,2 с. Очевидно, що після дощу рівень води піднімається, отже, час падіння камінця зменшується. Тобто стає рівним 0,6 − 0,2 = 0,4 (с).

ℎ₂ = 5𝑡² = 5 ∙ (0,4)² = 5 ∙ 0,16 = 0,8 (м) – відстань/рівень води після

дощу.

Тепер, ми можемо знайти на скільки має піднятися рівень води після дощу:

ℎ = ℎ₁ − ℎ₂ = 1,8 − 0,8 = 1 (м)

Відповідь: На 1 м має піднятися рівень води після дощу, щоб час, що вимірюється, змінився на 0,2 с.

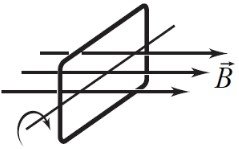Задача 2. Під час обертання дротяної рамки у магнітному полі потік магнітної індукції, який пронизує її, змінюється залежно від часу за законом Ф(𝑡) = 0,02𝑠𝑖𝑛20𝜋𝑡. Знайдіть:

1) Амплітуду

2) Фазу

3) Початкову фазу

4) Кутову швидкість

5) Частоту

6) Циклічну частоту

7) Період обертання

Розв’язання

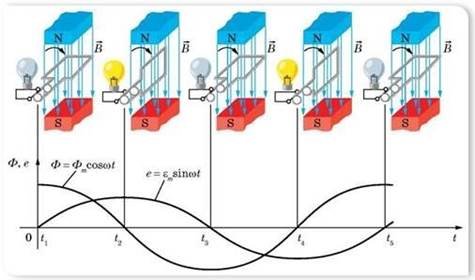
Згадаємо з фізики, що рамка обертається рівномірно з кутовою швидкістю 𝜔 за годинниковою стрілкою, отже, в будь-який момент часу 𝑡 кут повороту 𝜑 рамки 𝜑 = 𝜔𝑡. Відповідно значення магнітного потоку, який пронизує рамку, змінюється за законом Ф = 𝐵𝑆 ∙ 𝑐𝑜𝑠(𝜔𝑡) = Ф_𝑚 ∙ 𝑐𝑜𝑠(𝜔𝑡). Ця формула визначає зміну магнітного потоку через контур рамки площею 𝑆, яка рівномірно обертається в однорідному магнітному полі індукцією 𝐵 з кутовою швидкістю 𝜔.

Згадаємо, які величини входять до рівняння коливального руху.

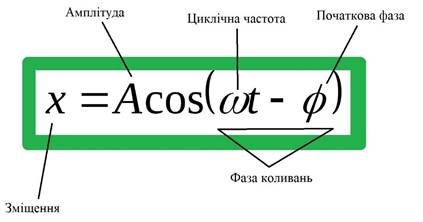
1) Знайдемо амплітуду. Амплітуда коливань – це максимальне усунення тіла від положення рівноваги.

З закону ми бачимо, що Ф(𝑡) = 0,02𝑠𝑖𝑛20𝜋𝑡. Тобто амплітуда буде 𝐴 =

0,02

2) Фаза коливань – це аргумент періодичної функції, який при заданій амплітуді коливань визначає стан коливальної системи будь-якої миті часу.

Фаза коливання: 𝜑 = 20𝜋𝑡

3) Початкова фаза – це 𝜑₀.

Початкова фаза: 𝜑₀ = 0

4) Кутова швидкість – це фізична величина, що дорівнює відношенню куту повороту радіуса-вектору, до часу за який цей поворот відбувся. Формула:

2𝜋

𝜔 = ; 𝜔 = 2𝜋𝑣

𝑇

Кутова швидкість: 𝜔 = 20𝜋

𝜔 1

5) Частота – це число обертів за одиницю часу. Формула: 𝑣 = ; 𝑣 =

2𝜋 𝑇

Знайдемо частоту, для того щоб знайти частоту коливання потрібно знати

20𝜋 кутову швидкість. Застосуємо формулу: 𝑣 = = 10

2𝜋

6) Циклічна частота – це число коливань за 2𝜋 секунд. Формула: 𝜔₀ =

2𝜋

= 2𝜋𝑣

𝑇

Знайдемо циклічну частоту: 𝜔₀ = 2𝜋𝑣 = 2𝜋 ∙ 10 = 20𝜋

2𝜋

Знайдемо циклічну частоту іншим способом, через період: 𝜔₀ ⁼ _𝑇 =

𝜋

7) Період обертання – це проміжок часу, протягом якого тіло робить одне

2𝜋 1 повне коливання. Формула: 𝑇 = ; 𝑇 =

𝜔 𝑣

2𝜋

Знайдемо період обертання (коливання) через кутову швидкість: 𝑇 = =

𝜔

2𝜋 1 = = 0,1

20𝜋 10

Знайдемо період обертання (коливання) іншим способом, через частоту:

1 1

𝑇 = = = 0,1

𝑣 10

Математика і хімія

Задача 1. Є 2 посудини, що містять відповідно 4 та 6 кг розчину кислоти різних концентрацій. Якщо їх злити разом, то вийде розчин, що містить 35% кислоти. Якщо злити рівні маси цих розчинів, то вийде 36% розчин. Скільки кг кислоти міститься у кожному розчині?

Розв’язання

Нехай 𝑥 кілограм маса речовини у першому розчині, 𝑦 - кілограм маса речовини у другому розчині, 0 < 𝑥 < 4; 0 < 𝑦 < 6

	Маса розчина	% вмісту розчину	Маса речовини
Перший розчин	4	𝑥 ∙ 100% 4	𝑥
Другий розчин	6	𝑦 ∙ 100% 6	𝑦
Перший + Другий розчин	4 + 6 = 10	35%	0,35 ∙ 10
Перший розчин	10	𝑥 ∙ 100% 4	𝑥
Другий розчин	10	𝑦 ∙ 100% 6	𝑥
Перший + Другий розчин	20	36	0,36 ∙ 20

Складемо і розв’яжемо систему:

𝑥 + 𝑦 = 3,5

{ 5𝑦

2,5𝑥 + = 7,2 3

𝑥 = 3,5 − 𝑦, підставимо замість 𝑥 значення 3,5 − 𝑦.

5𝑦

8,75 − 2,5𝑦 + = 7,2 3

−2,5𝑦 + 𝑦 = 7,2 − 8,75

5 5

− 𝑦 + 𝑦 = 7,2 − 8,75

2 3

𝑦

𝑦 другий розчин

Знайдемо тепер перший розчин: 𝑥 + 𝑦 = 3,5 ⇒ 𝑥 = 3,5 − 𝑦 = 3,5 − 1,86 = 1,64 (кг)

Відповідь: І розчин – 1,64 кг, ІІ розчин – 1,86 кг.

Задача 2. Є два сплави. Перший містить 10% нікелю, а другий – 25% нікелю. З цих двох сплавів отримали третій метал масою 200 кг, що містить 25% нікелю. На скільки кілограмів маса першого сплаву менша за масу другого?

Розв’язання

Складемо схему

Нехай перший сплав – x (кг), тоді другий сплав – y (кг). Тоді всього вийде:

10% 30% 25%

𝑥 + 𝑦 = 200. Отже, друге рівняння буде 𝑥 + 𝑦 = ∙ 200

100% 100% 100%

Складемо систему:

𝑥 + 𝑦 = 200

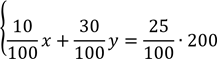
𝑥 + 𝑦 = 200 𝑥 + 𝑦 = 200

{ ⇒ {

0,1𝑥 + 0,3𝑦 = 25 ∙ 2 0,1𝑥 + 0,3𝑦 = 50

Помножимо перше рівняння на −0,3

𝑥 + 𝑦 = 200 −0,3𝑥 − 0,3𝑦 = −60

{ | ∙ (−0,3) ⇒ {

0,1𝑥 + 0,3𝑦 = 50 0,1𝑥 + 0,3𝑦 = 50

Додамо тепер ці рівняння:

−0,3𝑥 + 0,1𝑥 − 0,3𝑦 + 0,3𝑦 = −60 + 50

−0,2𝑥 = −10 ⇒ 𝑥 = (−10) ∶ (−0,2) = 50 (кг) − перший сплав

Знайдемо тепер перший сплав:

50 + 𝑦 = 200 ⇒ 𝑦 = 200 − 50 = 150 (кг) − другий сплав

Різниця: 150 − 50 = 100 (кг)

Відповідь: На 100 кілограмів маса першого сплаву менша за масу другого.

Математика і економіка

Задача 1. Підприємство «Львівська Кондитерська Фабрика «Світоч» виробляє та продає товари. За попередній місяць було вироблено 800 тис. одиниць товару. Вартість сировини для виробництва одного товару становить 100 грн, а зарплата працівникам – 500 грн. Доход від продажу одного товару складає 1000 грн. Підприємство також має фіксовані щомісячні витрати в розмірі 100 тис. грн. Знайдіть прибуток підприємства за попередній місяць.

Розв’язання

1. Вартість виробництва одного товару складає:

100 грн (сировина) + 500 грн (оплата праці) = 600 грн 2. Доход від продажу одного товару становить 600 грн.

3. Прибуток від одного товару становить:

1000 грн (вартість продажу) - 600 грн (вартість виробництва) = 400 грн

4. Прибуток від 800 тис. одиниць товару складає:

100 грн (прибуток від одного товару) * 800 тис. (кількість товару) = 80 млн. грн

5. Фіксовані щомісячні витрати становлять 100 тис. грн.

6. Прибуток підприємства за попередній місяць складає:

80 млн. грн (прибуток від продажу) – 100 тис. грн (фіксовані витрати) = 79 900 000 грн

Отже, прибуток підприємства за попередній місяць складає 79 900 000 грн.

Відповідь: Прибуток підприємства за попередній місяць складає 79 900 000 грн.

Задача 2. Мирон вніс на депозитний рахунок 50 тис. грн під 10% річних. Скільки коштів буде на цьому рахунку через 6 років? Скільки відсоткових коштів матиме Мирон через 6 років?

Розв’язання

𝐴₀ = 50 000 грн., 𝑝 = 10%, 𝑛 = 6 років

𝑝 𝑛

𝐴_𝑛 = 𝐴₀ (1 + ) 100

𝐴

Відсоткові кошти можна знайти як різницю 𝐴

𝐴

Відповідь: 88 578,05 грн буде на цьому рахунку через 6 років. 38 578,05 грн відсоткових коштів матиме Мирон через 6 років.

Математика та інформатика

Задача 1. У виконавця Акорд дві команди, яким присвоєно номери:

1. Додай 2.

2. Помнож на 𝑥.

де 𝑥 – невідоме додатнє число. Виконуючи першу з них, Акорд додає до

числа на екрані 1, а виконуючи другу, множить це число на 𝑥.

Програма для виконавця Акорд – це послідовність номерів команд. Відомо, що програма 121112 переводить число 4 до 36. Визначте значення 𝑥.

Розв’язання

Виконаємо програму, використовуючи шукане 𝑥 як змінну:

Програма 121112 переводить число 4 до 36.

Початковий вхід: 4

1: 4 + 2 = 6

2: 6 ∙ 𝑥 = 6𝑥

1: 6 ∙ 𝑥 + 2 = 6𝑥 + 2

1: (6 ∙ 𝑥 + 2) + 2 = 6𝑥 + 2 + 2 = 6𝑥 + 4

1: ((6 ∙ 𝑥 + 2) + 2) + 2 = 6𝑥 + 2 + 2 + 2 = 6𝑥 + 6

2: (6 ∙ 𝑥 + 6) ∙ 𝑥 = 6𝑥² + 6𝑥

Кінцевий вихід: 36

Прирівнюємо отриманий вираз до значення, яке виходить на виході програми.

6𝑥² + 6𝑥 = 36

Вирішуємо рівняння:

6𝑥² + 6𝑥 = 36 | ∶ 6

𝑥² + 𝑥 = 6 ⇒ 𝑥² + 𝑥 − 6 = 0

{𝑥1 + 𝑥₂ = −1;

𝑥₁ ∙ 𝑥₂ = −6;

𝑥₁ = −3 ∪ 𝑥₂ = 2

Коріння: −3, 2

Відповіддю є 2 ціле додатнє рішення.

Задача 2. Файл розміром 3000 Кбайт передається через деяке з'єднання протягом 160 секунд. Визначте розмір файлу (Кбайт), який можна передати через це з’єднання за 13 секунд. У відповіді вкажіть одне число — розмір файлу Кбайт. Одиниці виміру писати не потрібно.

Розв’язання Використаємо формулу: 𝐼 = 𝑉 ∙ 𝑡.

𝑉 – пропускна здатність каналу (у бітах за секунду або подібних одиницях);

𝑡 – час передачі.

Знайдемо швидкість передачі інформації щодо з’єднання.

𝐼 3000 Кбайт

𝑉 = = ( ) = 18 Кбайт.

𝑡 160 с

Знайдемо обсяг файлу, який можна передати за 13 секунд.

Кбайт

𝐼 = 𝑉 ∙ 𝑡 = 18 () ∙ 13 (с) = 234 Кбайт. с

Відповідь: 234Кбайт розмір файлу, який можна передати через це

з’єднання за 13 секунд.

Математика та музика

Задача 1. Додайте значення ритму нот і пауз нижче. Не впевнені у значеннях? Для того, щоб виконати це завдання перегляньте підказки. Перевірте діаграму на наявність нагадувань.

	Математична музика

1 біт	1 біт	1 біт	2 біта	2 біта	4 біта

Приклади:

Розв’язання

За допомогою підказки ми можемо розв’язати ці приклади.

	1 + 1 = 2		2 + 1 + 1 = 4
	2 + 1 = 3		2 + 1 + 1 = 4
	1 + 2 = 3		2 + 2 + 4 + 2 + 1 = 11
	5 ∙ 2 = 10		4 + 1 + 2 + 1 = 8
	4 − 1 = 3		2 + 1 + 4 + 1 + 4 = 12

Задача 2. У давні часи, коли нотний стан тільки з’явився, він був пустим і безжиттєвим. Проте, з часом він набував сили та магії завдяки нотам, які з’явилися на його лініях.

У маленькому селі жив хлопчик на ім’я Максим. Його доля була пов’язана з музикою, і він завжди мріяв стати відомим композитором. Він прагнув знайти спосіб втілити свої музичні ідеї на папері.

В один особливий день, а саме в день народження. Максим отримав від своїх батьків подарунок – старовинний нотний стан. Він був виготовлений зі старих пергаментів та виглядав неймовірно чарівно. Максим розташував нотний стан перед собою, маючи на увазі свою дату народження. Він знаряддями музиканта почав розміщувати ноти на лініях, несучи в собі свої почуття та настрої.

Перша нота, яку він намалював, була нота «Мі», яка відповідала дню народження. Вона символізувала його внутрішній голос та музичний талант. Наступні ноти, «Ре», «Соль», «Ля», «Сі» та «Фа», з’явилися на нотному стані, утворюючи мелодію, яка розповідала про його унікальну особистість та почуття.

Максим занурився в магію нотного стану. Кожна нота, кожен акорд, який він створював, був часткою його душі. Він писав музику, яка говорила про його рідне село, про кохання та мрії, про радість та сум. З кожним наступним днем, Максим розвивав свій талант і ставав все відомішим. Його композиції виконувалися на концертах та прославляли його село.

Нотний стан став місцем, де кожна нота мала своє місце, свою роль у створенні музичних шедеврів. Він став місцем зустрічі Максима з його власним потенціалом та творчістю. Кожен, хто слухав музику Максима, міг відчути магію та силу нотного стану. Він переносив слухачів в інший світ, де музика відбивалася в серцях та доторкалася до найглибших почуттів. Так пройшли роки, але магія нотного стану залишалася незмінною. Він продовжував надихати музикантів, розкривати їхні таланти та допомагати втілювати музичні ідеї.

І досі, коли звуки музики лунають у повітрі, нотний стан стоїть там, готовий прийняти нові ноти та створити нову історію. Він нагадує нам, що музика – це мова, що об’єднує серця та перетворює найпотаємніші емоції в чарівні мелодії.

Шановні діти, ви прослухали історію Максима, як він став найвідомішим композитором завдяки мелодії. Він створив мелодію на нотному стані за допомогою своєї дати народження. Зараз ви спробуєте розпізнати ноти на нотному стані і для цього вам потрібно виконати такі наступні завдання:

1) Розпізнати та записати ноти (записати цифри) на заданих лініях нотного стану.

2) Скласти музичний рядок з нот, відповідних їх даті народження (записати ноти).

3) Відгадайте прізвища та ім’я учнів по даті народження.

1.
2.
3.
4.
5.
6.

Кожному числу у даті народження відповідає певна нота музичного ладу.

Надайте учням надається таблиця, де зазначені числа та ноти, яким вони відповідають.

Примітка

Позначення нот	Цифра ноти	Нота	Позначення нот	Цифра ноти	Нота
	0	До		5	Ля
	1	Ре		6	Сі
	2	Мі		7	До
	3	Фа		8	Ре
	4	Соль		9	Мі